J. Cent. South Univ. Technol. (2011) 18: 760-766
DOI: 10.1007/s11771-011-0760-0
Adaptive control using interval Type-2 fuzzy logic for uncertain nonlinear systems
ZHOU Hai-bo(周海波)1, 2, YING Hao(应浩)3, DUAN Ji-an(段吉安)1, 2
1. School of Mechanical and Electrical Engineering, Central South University, Changsha 410083, China;
2. State Key Laboratory of High Performance and Complex Manufacturing,
Central South University, Changsha 410083, China;
3. Department of Electrical and Computer Engineering, Wayne State University, Detroit, Michigan, 48202, USA
? Central South University Press and Springer-Verlag Berlin Heidelberg 2011
Abstract: A new adaptive Type-2 (T2) fuzzy controller was developed and its potential performance advantage over adaptive Type-1 (T1) fuzzy control was also quantified in computer simulation. Base on the Lyapunov method, the adaptive laws with guaranteed system stability and convergence were developed. The controller updates its parameters online using the laws to control a system and tracks its output command trajectory. The simulation study involving the popular inverted pendulum control problem shows theoretically predicted system stability and good tracking performance. And the comparison simulation experiments subjected to white noise or step disturbance indicate that the T2 controller is better than the T1 controller by 0-18%, depending on the experiment condition and performance measure.
Key words: Type-2 fuzzy systems; adaptive fuzzy control; nonlinear systems; stability
1 Introduction
A fuzzy logic system that employs the Type-2 (T2) fuzzy sets and/or T2 fuzzy logic and inference is called a T2 fuzzy system. In contrast, a fuzzy logic system using ordinary (i.e., T1) fuzzy sets, logic and inference is called T1 fuzzy system [1-2]. Accordingly, there are two kinds of adaptive fuzzy control: T1 adaptive fuzzy control and T2 adaptive fuzzy control.
T2 fuzzy set is an extension of T1 fuzzy set. It is a three-dimensional system and includes a spatial uncertainty band, so the T2 fuzzy set is supposed to have a better capability of modeling uncertainties [3]. Literatures show that the fuzzy control using T2 fuzzy sets can outperform the T1 fuzzy control [4-6]. How to realize a novel configuration of T2 adaptive fuzzy controllers? How do the input T2 fuzzy sets influence the control performance? The discussion about these questions has important significance. There are few literatures that discuss T2 adaptive fuzzy control [7-8]. There appear two main weaknesses in Ref.[7]. First, the fuzzy system adopted in the adaptive fuzzy control must be able to universally approximate any continuous function to any desired accuracy, which is a premise for any adaptive fuzzy control [9]. But, method in Ref.[7] fails to show evidence that this is the case for the controller. Second, the KM iterative type-reducer is used to configure the T2 adaptive fuzzy controller. Hence, the ascending-order arranged T2 consequent fuzzy sets are used for the iterative computation. Nevertheless, this should not be doable as there are unknown adaptive parameters in the fuzzy sets.
In the present work, a T2 adaptive fuzzy controller that does not suffer the weaknesses was proposed. There are two types of adaptive control: direct adaptive control and indirect adaptive control. The latter scheme was adopted. Also, a simple type-reducer was used to avoid the complex iterative computation. Then, to quantify how much the T2 fuzzy control is better than its T1 counterpart, a genetic algorithm was used to optimize the controller parameters and compare their performance under various settings in simulation using the benchmark test model of the inverted pendulum.
2 Novel Type-2 adaptive fuzzy controller
This controller is to control a class of n-th order uncertain nonlinear systems:
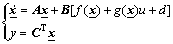 (1)
(1)
where
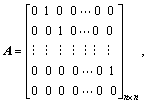
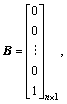
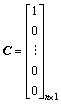
and 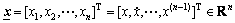 is a state
is a state
vector. u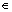 R and y
R and y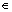 R are input and output of the systems, respectively. d is an external bounded uncertain disturbance, and
R are input and output of the systems, respectively. d is an external bounded uncertain disturbance, and  and
and  are unknown bounded continuous functions with
are unknown bounded continuous functions with 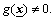
An adaptive fuzzy controller  was designed to control the plant so that its output follows a reference trajectory ym, where
was designed to control the plant so that its output follows a reference trajectory ym, where  and
and 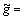
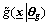 are T2 fuzzy universal approximators to be designed to approximate
are T2 fuzzy universal approximators to be designed to approximate  and
and  , respectively. Here,
, respectively. Here, 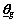 and
and 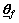 are parameters updated by the adaptive laws. Assuming that 1)
are parameters updated by the adaptive laws. Assuming that 1) 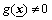 ,
,  and
and  are bounded for all
are bounded for all 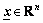 , and the plant is feedback linearizable by static-state feedback; 2) all the signals are uniformly bounded:
, and the plant is feedback linearizable by static-state feedback; 2) all the signals are uniformly bounded: 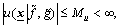
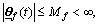
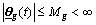 and
and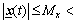 ∞ or all t≥0, where Mu, Mf, Mg and Mx are the design parameters specified by the designer [10]. The global system stability is achieved by using the Lyapunov theory, that is,
∞ or all t≥0, where Mu, Mf, Mg and Mx are the design parameters specified by the designer [10]. The global system stability is achieved by using the Lyapunov theory, that is, 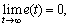 where e=ym-y is the tracking error.
where e=ym-y is the tracking error.
The working process of the T2 adaptive fuzzy control is similar to that of the adaptive T1 fuzzy control except the inclusion of the type-reducer. The crisp inputs are first fuzzified by the input T2 fuzzy sets (i.e. antecedent fuzzy sets); then the T2 fuzzy sets activate the inference engine and the rule base to produce output T2 fuzzy sets (i.e., consequent fuzzy sets—they are singleton T2 fuzzy sets). These fuzzy sets are then processed by the type-reducer which combines the output sets using the centroid calculation, leading to the T1 fuzzy sets (called the type-reducer sets). Finally, these sets are defuzzified to create a crisp output. In this work, mp different Gaussian interval T2 fuzzy sets were adopted for xp. To cover the entire input space, there are
up to 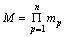 different output fuzzy sets used in the fuzzy rules.
different output fuzzy sets used in the fuzzy rules.
The T2 fuzzy approximators 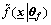 and
and 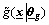 have the same mathematical form. For brevity, only
have the same mathematical form. For brevity, only 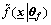 was described here. Consider the state variables
was described here. Consider the state variables 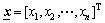 in Eq.(1) to be the inputs of
in Eq.(1) to be the inputs of 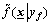 and its output is yf. Let the i-th rule be
and its output is yf. Let the i-th rule be
IF x1 is 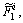 x2 is
x2 is 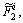 …, xn is
…, xn is 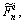
THEN yf is 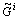 (2)
(2)
where the T2 input fuzzy sets and the T2 output fuzzy sets are denoted by 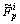 (i=1, …, M) and
(i=1, …, M) and 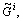 respectively, with their respective membership functions being
respectively, with their respective membership functions being 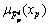 and
and 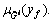
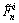 is from
is from 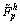 (h=1, …, mp). When the secondary membership function of a T2 fuzzy set is constantly 1, the uncertainty zone contained in the primary memberships forms a bounded region called footprint of uncertainty (FOU) [3]. The bound of a FOU can be divided into two T1 membership functions: an upper membership function
(h=1, …, mp). When the secondary membership function of a T2 fuzzy set is constantly 1, the uncertainty zone contained in the primary memberships forms a bounded region called footprint of uncertainty (FOU) [3]. The bound of a FOU can be divided into two T1 membership functions: an upper membership function 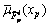 (and
(and  ) and a lower membership function
) and a lower membership function 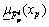 (and
(and 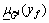 ).
).
There are many kinds of type-reduction methods, such as centroid, height, modified weight and center-of- sets [3, 11-12]. The center-of-sets type-reducer is used in this work:
 (3)
(3)
where 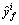 is a value of yf at which
is a value of yf at which 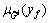 achieves its maximum value.
achieves its maximum value.  is the firing interval of the i-th rule and
is the firing interval of the i-th rule and 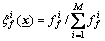 . Viewing
. Viewing 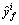 in Eq.(3) as an
in Eq.(3) as an
adaptive parameter and defining an adaptive parameter vector 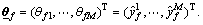 And regarding
And regarding 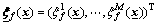 as a T2 fuzzy regressive vector. Thus, Eq.(3) can be rewritten as
as a T2 fuzzy regressive vector. Thus, Eq.(3) can be rewritten as
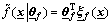 (4)
(4)
Logically, the other T2 fuzzy approximator can be expressed as
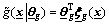 (5)
(5)
where 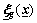 is a T2 fuzzy regressive vector, and
is a T2 fuzzy regressive vector, and 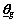 is an adaptive parameter vector.
is an adaptive parameter vector.
Putting all these together, the T2 adaptive fuzzy controller can be written as
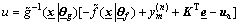 (6)
(6)
where 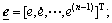
 is the feedback gain vector to make the characteristic polynomial of A-BKT Hurwitz; ua is an adaptive robust term used to finely tune the controller.
is the feedback gain vector to make the characteristic polynomial of A-BKT Hurwitz; ua is an adaptive robust term used to finely tune the controller.
And now the specific control law ua and adaptive laws 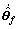 and
and 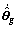 are needed to develop to update the parameters
are needed to develop to update the parameters 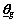 and
and 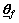 . Substituting Eq.(6) into Eq.(1) yields the following error equation:
. Substituting Eq.(6) into Eq.(1) yields the following error equation:
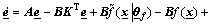
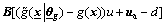 (7)
(7)
Define the optimal parameter vectors 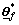 and
and 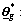
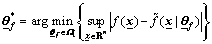 (8)
(8)
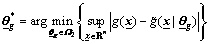 (9)
(9)
where 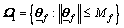 and
and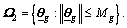
Furthermore, define the fuzzy approximator error:
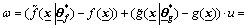
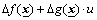 (10)
(10)
Let 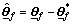 and
and 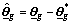 and combine Eq.(6) and Eq.(10), then the error Eq.(7) can be rewritten as
and combine Eq.(6) and Eq.(10), then the error Eq.(7) can be rewritten as
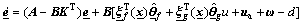 (11)
(11)
Consider a Lyapunov function:
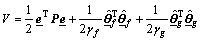 (12)
(12)
where 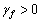 and
and 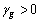 are adaptation gains, P≥0 is a weighing matrix with P=PT. The time derivative of V is
are adaptation gains, P≥0 is a weighing matrix with P=PT. The time derivative of V is
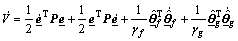 (13)
(13)
Substituting Eq.(11) into Eq.(13) yields
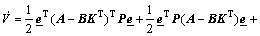

 (14)
(14)
where 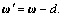
Since how to choose some adaptation laws 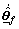 and
and 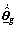 and control law ua to make
and control law ua to make 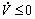 is the key task, the following Riccati-like equation is constructed:
is the key task, the following Riccati-like equation is constructed:
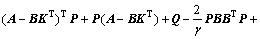
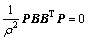 (15)
(15)
where 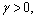 is a gain parameter to be designed for ua;
is a gain parameter to be designed for ua; 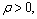 is an attenuation parameter for coping with the error ω′; weighing matrix Q=QT≥0. Choose the adaptive control laws as
is an attenuation parameter for coping with the error ω′; weighing matrix Q=QT≥0. Choose the adaptive control laws as
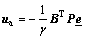 (16)
(16)
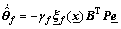 (17)
(17)
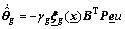 (18)
(18)
Combining Eqs.(14)-(18) yields
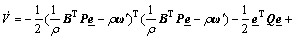
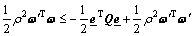 (19)
(19)
Then, integrating the above equation from t=0 to t=t′ yields
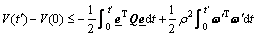 (20)
(20)
Since 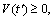 inequality Eq.(20) implies
inequality Eq.(20) implies
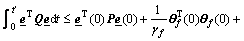
 (21)
(21)
where 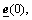
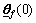 and
and 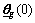 mean the values of
mean the values of 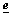 ,
, 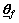 and
and 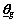 at t=0, respectively. If ρ, Q, P, γ, γf, γg,
at t=0, respectively. If ρ, Q, P, γ, γf, γg, 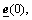
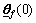 and
and 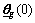 are chosen to satisfy Eq.(15) and Eq.(21), the closed-loop system stability will be achieved. Based on Eq.(17) and Eq.(18), the T2 fuzzy approximator parameters
are chosen to satisfy Eq.(15) and Eq.(21), the closed-loop system stability will be achieved. Based on Eq.(17) and Eq.(18), the T2 fuzzy approximator parameters 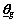 and
and 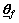 can be updated online. Using Eqs.(4), (5) and (16), the T2 adaptive fuzzy controller can achieve its control goal.
can be updated online. Using Eqs.(4), (5) and (16), the T2 adaptive fuzzy controller can achieve its control goal.
Note that all the structure and derivations of the T2 adaptive fuzzy control system are based on the premise that 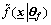 and
and 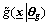 can be used to approximate
can be used to approximate  and
and 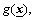 respectively, via Eq.(4) and Eq.(5). How to realize the T2 fuzzy universal approximators so that they can universally approximate any continuous function to any desired accuracy is an important issue.
respectively, via Eq.(4) and Eq.(5). How to realize the T2 fuzzy universal approximators so that they can universally approximate any continuous function to any desired accuracy is an important issue.
The firing interval of the i-th rule 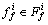 in Eq.(3) is an interval T2 fuzzy set, not a crisp value. And
in Eq.(3) is an interval T2 fuzzy set, not a crisp value. And 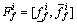 is determined by its leftmost and rightmost points
is determined by its leftmost and rightmost points 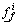 and
and 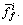 With the use of the singleton fuzzifier and product inference in this work,
With the use of the singleton fuzzifier and product inference in this work, 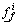 and
and 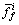 can be obtained:
can be obtained:
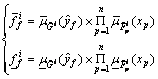 (22)
(22)
By the way, there is no restriction on the fuzzy AND and OR operators and the inference method, and other fuzzy AND and/or OR operators and other inference methods are also allowed to be used in different fuzzy rules. Note that unlike the T1 adaptive fuzzy control, the membership functions of the T2 adaptive fuzzy controller are not limited to the Gaussian type any more. There are many kinds of membership functions such as the triangular type. If one uses the Gaussian type (e.g., Fig.1), the primary membership functions for xp can be expressed as
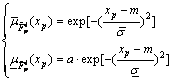 (23)
(23)
where 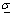 and
and 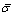 (
(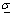 ≤
≤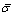 ) are the standard deviations, a (0
) are the standard deviations, a (0
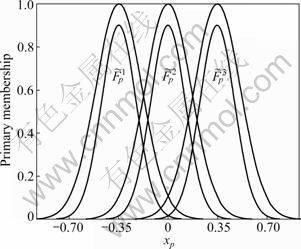
Fig.1 Three Gaussian interval T2 input fuzzy sets for x1 and x2 (i.e. xp where p=1, 2)
For the membership functions of the singleton T2 output fuzzy sets, there is
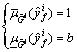 (24)
(24)
where 0
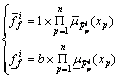 (25)
(25)
Properly choosing  from
from  is a key. In Ref.[13], KARNIK et al proposed a KARNIK-MENDEL (KM) iterative procedure (i.e. type-reducer) to search
is a key. In Ref.[13], KARNIK et al proposed a KARNIK-MENDEL (KM) iterative procedure (i.e. type-reducer) to search  from
from 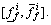 This iterative process is very complicated [14]. In this work, a simple method which avoids the weakness in computing
This iterative process is very complicated [14]. In this work, a simple method which avoids the weakness in computing  is adopted. From Eq.(22), one can see that there are two different membership functions for every rule and there are a total of 2M different membership functions for all the fuzzy rules. If
is adopted. From Eq.(22), one can see that there are two different membership functions for every rule and there are a total of 2M different membership functions for all the fuzzy rules. If  is chosen just as either
is chosen just as either 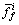 or
or 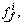 since there are M upper membership values and M lower membership values, there are 2M different combinations of the upper and lower membership values. Therefore, there are 2M type-reducer sets
since there are M upper membership values and M lower membership values, there are 2M different combinations of the upper and lower membership values. Therefore, there are 2M type-reducer sets 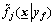 as Eq.(3) holds with j ranging from 1 to 2M. Then, the center-average defuzzifier is used to convert the 2M T1 fuzzy sets to a crisp output:
as Eq.(3) holds with j ranging from 1 to 2M. Then, the center-average defuzzifier is used to convert the 2M T1 fuzzy sets to a crisp output:
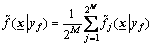 (26)
(26)
Combining Eq.(3) and Eq.(26) yields
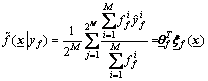 (27)
(27)
where 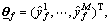 is an adjustable parameter, and
is an adjustable parameter, and 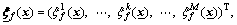 is the regressive vector with the regressor
is the regressive vector with the regressor 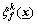 being defined as
being defined as
 (28)
(28)
In Ref.[2], it has been proved that the T2 fuzzy systems (Eq.(27)) can uniformly approximate any continuous function on a compact domain to any arbitrary accuracy. So, the proposed adaptive controller relies mathematically on the universal approximation theorem.
3 Simulation study
3.1 Inverted pendulum control problem
The T2 adaptive fuzzy controller is used to control an inverted pendulum [7, 15]. Let x1=θ be the angle of the pendulum with respect to the vertical line and 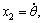 then the dynamic equations of the inverted pendulum system are
then the dynamic equations of the inverted pendulum system are
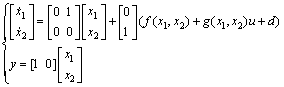 (29)
(29)
where 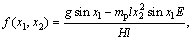
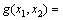
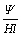 with
with 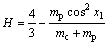 and
and 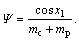 g=
g=
9.8 m/s2 is the acceleration due to gravity. mc and mp are the masses of the cart and the pole, respectively, and l is the half length of the pole. u is the applied force which is the control input, and d is external disturbance. Assume that mc=1 kg, mp=0.1 kg and l=0.5 m.
The step size h=0.001 and the forth-order Runge- Kutta method are used to integrate the differential equations of the system and the adaptive laws in Eq.(17) and Eq.(18) with the initial system conditions x1(0)=0.05 and x2(0)=0.3. The objective of the simulation study is to make x1 follow one of the two reference trajectories at a time: 1) step function ym1(t)=0.2, and 2) sinusoidal function ym2(t)=0.2sint. Let the external disturbance d(t)=0.1sint and use the following control performance measure:
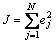 (30)
(30)
where N is the total number of time steps and ej is the system output tracking error at the j-th step. The performance measurements JT1 and JT2 are used to denote the control performances of the T1 and T2 adaptive fuzzy controls, respectively.
To study the control performance under noise, a white noise is added to the system output whose maximum amplitude is 5% of the maximum system reference trajectory amplitude. How well the system can handle disturbance is also tested. A constant disturbance of magnitude 10 is also added to the controller output u(t) temporally between t=7 s and t=7.2 s.
3.2 Genetic algorithm optimized adaptive T2/T1 fuzzy controllers
Three (i.e. m1=m2=3) interval T2 fuzzy sets are used for both x1 and x2 (Fig.1). They are 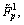
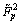 and
and 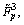 whose upper membership functions (
whose upper membership functions (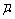 ) and lower membership functions (
) and lower membership functions (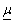 ) are chosen respectively as (p=1, 2)
) are chosen respectively as (p=1, 2)
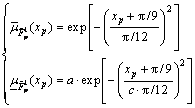 (31a)
(31a)
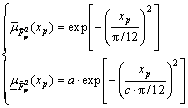 (31b)
(31b)
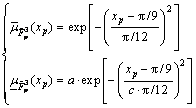 (31c)
(31c)
where a is the FOU width coefficient for the input fuzzy sets, and 0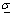 and
and 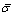 in Eq.(23) via
in Eq.(23) via 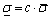 so that they are proportional. According to Eq.(1), it is obvious that there are M=m1× m2=9 fuzzy rules to approximate f(x1, x2) and g(x1, x2).
so that they are proportional. According to Eq.(1), it is obvious that there are M=m1× m2=9 fuzzy rules to approximate f(x1, x2) and g(x1, x2).
For control performance comparison, a T1 adaptive fuzzy controller was also designed. Its fuzzy sets adopted the upper membership functions of the T2 adaptive fuzzy controller. The structure of the controller, the control laws, the parameter update laws, the initial condition, the control objective and all the other designed parameters except γf, γg, γ and ρ were kept the same as those of the T2 adaptive fuzzy controller. Let k1=2 and k2=1 so that s2+k1s+k2 is stable. The following parameter values were used: θfi(0)=-2, θgi(0)=1.2, P=[115 5; 5 5] and Q= diag(120, 100)/11. The values of the parameters γf, γg, γ, ρ, a, b and c were optimized by the genetic algorithm in MATLAB’s Genetic Algorithm and Direct Search Toolbox (version: R2007a) and also by solving Eq.(15) and Eq.(21) to achieve the best control performance. The performance criteria were to achieve a shortest rise-time and minimal system output overshoot.
The number of generation was set at 200 for the GA. The default settings of the GA function were mostly used. The parameter search process was as follows. First, the initial search ranges for the design parameters γf, γg and γ were set to [0, 1 000], [0, 500] and [0, 200], respectively. 1 000 times GA for the T1 adaptive fuzzy controller was run to search for the best values of the corresponding parameters γf1, γg1 and γ1. Then, these results were used to set the new initial search ranges of γf, γg and γ to [0.8γf1, 1.2γf1], [0.8γg1, 1.2γg1] and [0.8γf1, 1.2γf1] for the T1 controller again. Afterwards, 500 times GA was run. The resulting parameter values were used by the T1 controller which was treated as the optimized controller. These values were also used as initial conditions for the GA to optimize the same parameters for the T2 adaptive controller. Additional parameters of the T2 controller to be optimized were a, b and c whose initial search ranges were in [0, 1]. 500 times GA were run again. The value of ρ can be computed using Eq.(15) for the T1 and T2 fuzzy controllers; it is not searched by the GA.
After running the GA, the optimized parameters for the T1 fuzzy controller are found to be γf1=242.84, γg1= 78.97 and γ1=22.72. Accordingly, ρ=0.83. And the optimized parameters for the T2 fuzzy controller are: γf2=227.12, γg2=69.81, γ2=22.59, a=0.87, b=0.80 and c=0.83. Correspondingly, ρ=0.92 is calculated.
3.3 Simulation results
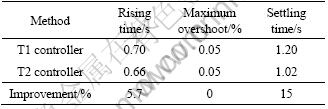
The performances of the T2 controller and their comparisons with the T1 controller are graphically shown in Figs.2-4. The performance measures are numerically given in Tables 1-2. Based on these results, the following observations can be made. First, the T2 adaptive fuzzy controller can indeed guarantee the theoretically ensured system stability and maintain a good tracking performance. Second, the T2 adaptive fuzzy controller can outperform the T1 fuzzy controller by varying degrees (up to 18%, see Tables 1 and 2), depending on the experiment condition and performance measure. The former has less rising time, smaller steady-state error, and better handling of the white noise. However, performance under the disturbance is identical for the two controllers.
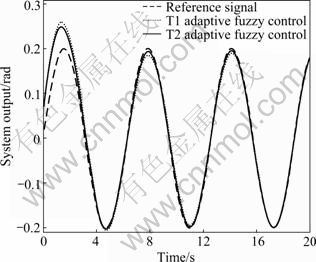
Fig.2 Tracking performance comparison between optimized T1 and T2 adaptive fuzzy control systems using inverted pendulum model
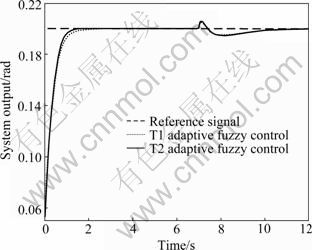
Fig.3 Performance comparison between optimized T1 and T2 adaptive fuzzy control systems (Responses to step command signal and to step disturbance are illustrated)
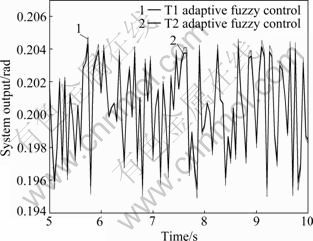
Fig.4 Tracking performance comparison between optimized T1 and T2 adaptive fuzzy control systems under white noise (Rest of 0-20 s result is not shown here for clarity)
Table 1 Quantitative summaries of performance comparisons shown in Figs.2-4

Table 2 Dynamic step response performance measures for Fig.3 (0-7 s)
4 Conclusions
1) A novel T2 adaptive fuzzy controller is developed, which is mathematically rigorous, and in that sense the controller is the only valid T2 adaptive controller in existence.
2) Computer simulation to quantify the performance of this new controller when it acts alone or in comparison with a comparable T1 adaptive fuzzy controller is conducted. The MATLAB genetic algorithm is used to optimize the performances of the controllers. The results show that the T2 controller is superior to the T1 controller to a certain extent (0-18%).
3) It remains an interesting open question whether the trends observed in this study hold true in general (e.g. in other system models and experiment conditions). The performance improvement by the T2 fuzzy logic is at the expense of system complexity. Whether such a tradeoff is worthwhile in practice is application-dependent.
References
[1] YING H. Constructing nonlinear variable gain controllers via the Takagi-Sugeno fuzzy control [J]. IEEE Trans Fuzzy Syst, 1998, 6(2): 226-234.
[2] YING H. General interval Type-2 mamdani fuzzy systems are universal approximators [C]// Proceedings of North American Fuzzy Information Processing Society. New York, USA, 2008: 294-299.
[3] MENDEL J M. Uncertain rule-based fuzzy logic systems: Introduction and new directions [M]. New Jersey: Prentice-Hall Press, 2001: 10-50.
[4] HANI H. Type-2 FLCs: A new generation of fuzzy controllers [J]. IEEE Trans Computational Intelligence Magazine, 2007, 2(1): 30-43.
[5] JOHN R, COUPLAND S. Type-2 fuzzy logic: A historical view [J]. IEEE Trans Computational Intelligence Magazine, 2007, 2(1): 57-62.
[6] RHEE F C. Uncertain fuzzy clustering: Insights and recommendations [J]. IEEE Trans Computational Intelligence Magazine, 2007, 2(1): 44-56.
[7] KHEIREDDINE C, LAMIR S, MOUNA G, KHIER B. Indirect adaptive interval Type-2 fuzzy control for nonlinear systems [J]. Int J Modelling, Identification and Control, 2007, 2(2): 106-119.
[8] ZHOU Hai-bo, YING H, DUAN Ji-an. T2 Adaptive fuzzy logic controller [C]// IEEE Conference on Fuzzy Systems. Seoul, Korea, 2009: 836-841.
[9] WANG Li-xin. Fuzzy systems are universal approximators [J]. IEEE Trans Fuzzy Syst, 1992, 8(12): 1163-1170.
[10] LI Han-xiong, TONG Shao-cheng. A hybrid adaptive fuzzy control for a class of nonlinear MIMO systems [J]. IEEE Trans Fuzzy Syst, 2003, 11(1): 24-34.
[11] LIANG Qi-lian, MENDEL J M. Interval Type-2 fuzzy logic systems: Theory and design [J]. IEEE Trans Fuzzy Syst, 2000, 8(5): 535-550.
[12] MENDEL J M, JOHN R I, LIU F. Interval Type-2 fuzzy sets made simple [J] IEEE Trans Fuzzy Syst, 2006 14(6): 808-821.
[13] KARNIK N N, MENDEL J M, LIANG Q. Type-2 fuzzy logic systems [J]. IEEE Trans Fuzzy Syst, 1999, 7(6): 643-658.
[14] WU Hong-wei, MENDEL J M. Uncertainty bounds and their use in the design of interval Type-2 fuzzy logic systems [J]. IEEE Trans Fuzzy Syst, 2002, 10(5): 622-639.
[15] WANG Li-xin. Stable adaptive fuzzy controllers with application to inverted pendulum tracking [J]. IEEE Trans Systems, Man, and Cybernetics-Part B: Cybernetics, 1996, 26(5): 677-691.
(Edited by YANG Bing)
Foundation item: Project(51005253) supported by the National Natural Science Foundation of China; Project(2007AA04Z344) supported by the National High Technology Research and Development Program of China
Received date: 2009-09-09; Accepted date: 2010-05-20
Corresponding author: DUAN Ji-an, Professor, PhD; Tel: +86-731-88836858; E-mail: duanjian@mail.csu.edu.cn