Optimal setting and placement of FACTS devices using strength Pareto multi-objective evolutionary algorithm
来源期刊:中南大学学报(英文版)2017年第4期
论文作者:Amin Safari Mojtaba Bagheri Hossein Shayeghi
文章页码:829 - 839
Key words:strength Pareto multi-objective evolutionary algorithm; static var compensator (SVC); thyristor controlled series capacitor (TCSC); static voltage stability margin; optimal location
Abstract: This work proposes a novel approach for multi-type optimal placement of flexible AC transmission system (FACTS) devices so as to optimize multi-objective voltage stability problem. The current study discusses a way for locating and setting of thyristor controlled series capacitor (TCSC) and static var compensator (SVC) using the multi-objective optimization approach named strength pareto multi-objective evolutionary algorithm (SPMOEA). Maximization of the static voltage stability margin (SVSM) and minimizations of real power losses (RPL) and load voltage deviation (LVD) are taken as the goals or three objective functions, when optimally locating multi-type FACTS devices. The performance and effectiveness of the proposed approach has been validated by the simulation results of the IEEE 30-bus and IEEE 118-bus test systems. The proposed approach is compared with non-dominated sorting particle swarm optimization (NSPSO) algorithm. This comparison confirms the usefulness of the multi-objective proposed technique that makes it promising for determination of combinatorial problems of FACTS devices location and setting in large scale power systems.
Cite this article as: Amin Safari, Mojtaba Bagheri, Hossein Shayeghi. Optimal setting and placement of FACTS devices using strength Pareto multi-objective evolutionary algorithm [J]. Journal of Central South University, 2017, 24(4): 829-839. DOI: 10.1007/s11771-017-3485-x.
J. Cent. South Univ. (2017) 24: 829-839
DOI: 10.1007/s11771-017-3485-x

Amin Safari1, Mojtaba Bagheri2, Hossein Shayeghi3
1. Department of Electrical Engineering, Azarbaijan Shahid Madani University, Tabriz, Iran;
2. Sama Technical and Vocational Training College, Islamic Azad University, Bonab Branch, Bonab, Iran;
3. Technical Engineering Department, University of Mohaghegh Ardabili, Ardabil, Iran
 Central South University Press and Springer-Verlag Berlin Heidelberg 2017
Central South University Press and Springer-Verlag Berlin Heidelberg 2017
Abstract: This work proposes a novel approach for multi-type optimal placement of flexible AC transmission system (FACTS) devices so as to optimize multi-objective voltage stability problem. The current study discusses a way for locating and setting of thyristor controlled series capacitor (TCSC) and static var compensator (SVC) using the multi-objective optimization approach named strength pareto multi-objective evolutionary algorithm (SPMOEA). Maximization of the static voltage stability margin (SVSM) and minimizations of real power losses (RPL) and load voltage deviation (LVD) are taken as the goals or three objective functions, when optimally locating multi-type FACTS devices. The performance and effectiveness of the proposed approach has been validated by the simulation results of the IEEE 30-bus and IEEE 118-bus test systems. The proposed approach is compared with non-dominated sorting particle swarm optimization (NSPSO) algorithm. This comparison confirms the usefulness of the multi-objective proposed technique that makes it promising for determination of combinatorial problems of FACTS devices location and setting in large scale power systems.
Key words: strength Pareto multi-objective evolutionary algorithm; static var compensator (SVC); thyristor controlled series capacitor (TCSC); static voltage stability margin; optimal location
1 Introduction
For many years, voltage collapse problems in power systems are a permanent problem for electric utilities and a subject of great importance due to the events of voltage instability and collapses that have occurred worldwide [1]. However, voltage stability is one of the challenging problems grownup by the utilities. Voltage collapse is defined as the process by which the sequence of events accompanying voltage instability leads to a blackout or abnormally low voltage in a significant part of the system [2]. Voltage collapses usually happen on power systems that are heavily loaded, faulted or have reactive power shortage [2, 3]. In Ref. [4], the new formulation and solution method were used to find the allocation of FACTS devices for security enhancement against voltage collapse. Also, TCSC and SVC are used to keep bus voltages and ensure the voltage-stability margin. The advent of flexible ac transmission systems (FACTS) devices based on the advance of semiconductor technology opened up new opportunities for controlling the power flow and reducing the flow on the overloaded transmission line and increasing the employment of different ways to excess capability. The FACTS technology will offer direct and flexible control of power transfer. For practical power systems, different buses are differently sensitive to the overall power system voltage stability. Some buses are more and some are less. Under heavy loading, a technique to stay the system from voltage collapse is to produce reactive power support with FACTS devices at applicable locations. Locating of FACTS devices is that the simplest approach for electric utilities to improve the voltage profile and voltage stability margin of the network [5]. There are many techniques proposed in literature for optimal location of FACTS devices. In Ref. [6], the new optimal routing algorithm was used for loss minimization and voltage stability improvement in radial power systems. The algorithm can automatically detect the critical transmission paths that will result in voltage collapse when additional active or reactive loads are added. In Ref. [7], continuation power flow algorithm is applied to find the size and location of FACTS devices and authors recommend an analytically approach for determining the location and rating of series compensator to extend the steady state transfer capability in a vertical integrated power system. In Ref, [8], the optimal locations of FACTS devices are calculated by solving the economic load dispatch plus the cost of these devices, making the assumption that all transmission lines have these devices.
Recently, multi-objective algorithms for optimal placing of FACTS devices have become popular. The intelligent optimizers such as genetic algorithm (GA) [9] and particle swarm optimization (PSO) [10, 11] are used to determine the appropriate location and size of the FACTS devices. In these studies, fitness function based on multiple objectives is maximized. However, the minimum level of satisfaction between the objectives is not guaranteed in these algorithms. In Ref. [10], the PSO technique is employed to search out the optimal location of multi-type of FACTS devices, namely SVC, TCSC and UPFC with a minimum cost of installation and to improve the system loadability. In Ref. [12], the parametric approach was used to find the optimal location of SVC and UPFC for real power loss minimization and stability enhancement in a multi- machine system and simultaneously contingency analysis is additionally examined to determine the critical outages with respect to voltage security to evaluate the effect of SVC on the location analysis. In Ref. [13], the HBGAPSO was proposed to determine the optimal types and ratings of UPFC, TCSC, TCPST and SVC that ensure the minimal overall system cost function. The main aim of this work is to develop an algorithm for determining the optimal location of FACTS devices, based on power loss reduction, voltage stability and load voltage deviation, which is to be maximized. The different types of FACTS technologies and their different locations have different benefits. Using strength Pareto multi-objective evolutionary algorithm for optimization of location and setting of SVC and TCSC reduces total transmission losses and voltage deviation and additionally and improves the system loadability.
2 Multi-objective optimization
2.1 Main concepts
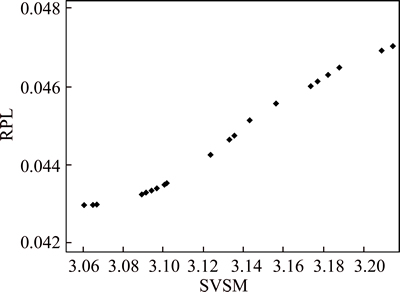
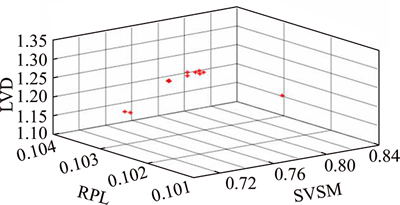
One way of handling a multi-objective problem is to combine the specified goals of the optimization problem and construct a scalar function and so apply a common scalar optimization approach to solve the problem. The major superiority of this approach is unavailability of any straightforward methods for combining the objectives of the problem while they vary constantly. One of the most successful multi-objective approaches is the SPMOEA [14]. To compare candidate solutions in multi-objective optimization problems, the concepts of Pareto dominance is employed. A decision vector v (denoted u In this case, the solution u dominates v; u is called the non-dominated solution. The solutions that are non-dominated between the intact research spaces are designated as Pareto-optimal set or the Pareto-optimal front [15]. 2.2 Strength Pareto evolutionary algorithm (SPMOEA) The basic elements of the SPMOEA technique are briefly stated and defined as follows [15]. 1) External set: It is a set of Pareto optimal solutions. These solutions are stocked externally and updated sequentially. Ultimately, the solutions stored in this set represent the Pareto optimal front. 2) Strength of a Pareto optimal solution: It is an assigned 3) Fitness of individuals: The fitness of each individual within the population is the sum of the strengths of all external Pareto optimal solutions by which it is covered. It is worth mentioning that the fitness of a population member is determined only from the individuals stored in the external set. This reduces extremely the computational burden of the fitness assignment approach. It is worth mentioning that the strength of the Pareto optimal solution is at the same time its fitness. Generally, the procedure can be described in the following steps [15]. Step 1: Initialization: Produce an initial population and make the vacuous external Pareto optimal set. Step 2: Update outside Pareto-optimal set. The outside Pareto optimal set is updated as follows. 1) Re-search the population for the non-dominated individual and copy them to the outside Pareto set. 2) Search the outer Pareto set for the non-dominated solutions and remove all dominated individuals from the set. 3) If the number of the individuals externally stocked in the Pareto set overstepped a pre-specified maximum size, decrease the set by means of clustering. Step 3: Fitness assignment. The fitness assignment procedure could be a two-stage method as follows. 1) The individuals in the external non-dominated set P* are ranked. The strength is commensurate to the number of individuals covered by that individual. 2) The objective function is evaluated by individuals in the population P. Step 4: Selection: The population and the external set individuals are combined and any two individuals are selected randomly. Based on their objective function, the better one is moved to the mating pool. Step 5: Crossover and Mutation. The thought behind crossover is to make an information exchange between two chromosomes. The objective of mutation is to create diversity in the population. Step 6: Termination. The stopping criterion is checked. If it is satisfied then, stop else copy new generation to old population and go to Step 2. The flowchart of the proposed algorithm is presented in Fig. 1. Fig. 1 Flowchart of strength Pareto implementation 2.3 OPF problem formulation The optimal power flow (OPF) is a nonlinear problem. The main goal of OPF is to optimize the settings of control variables in terms of one or a lot of objective functions whereas satisfying many equality and inequality constraints. In general, the OPF problem can be mathematically developed as follows [16]: Minimize f(x, u) (2) Subjected to g(x, u)=0 (3) h(x, u)≤0 (4) where f is the objective function to be optimized; g is the equality constraints representing nonlinear power flow equations; h is the system operating constraints. Also, u is the vector of independent control variables including: 1) Generator active power output PG except at slack bus PG1; 2) Generator bus voltage VG; 3) Transformer tap setting T; 4) Shunt VAR compensation QG. Hence u can be expressed as where Ng and Nt and denote the number of generating units, number of regulating transformers and number of shunt compensators, respectively. Generators active power (except slack bus) and generators bus voltages are continuous variable, while the tap setting of the changing transformers and VAR injections of the shunt capacitors are discrete variables. Also, x is the vector of dependent variables. Hence, x can be expressed as where Npq is the number of PQ buses; and Nt is the total number of transmission lines. 3 Modeling of FACTS devices Placing FACTS devices on a bus or a transmission line changes the amount of voltage or power in that location, as well as areas within the power network. In the present work, variable reactance is employed. 3.1 Modeling of TCSC The TCSC can serve as the capacitive or inductive compensation by directly modifying the reactance of the transmission line. In this work, the model of the TCSC has been developed to be appropriate for steady-state. It has modeled as variable reactance connected in series with transmission line. The model of transmission line with a TCSC connected between bus i and bus j is shown in Fig. 2 Fig. 2 Model of transmission line with TCSC The rated value of TCSC is a function of the reactance of transmission line where TCSC has been installed [17]: where XTCSC=KTCSC·Xline; Xline is the overall line reactance between buses i and j with TCSC installation; XTCSC is the reactance of TCSC and KTCSC is a coefficient which represents the compensation level of TCSC (-0.8< KTCSC<0.2). The working range of reactance of TCSC has been fixed between -0.8Xline and 0.2Xline. 3.2 Modeling of SVC Figure 3 presents the general equivalent model of SVC. It is composed of fixed capacitor and thyristor controlled reactor. The equivalent susceptance Beq is determined by the firing angle a of the thyristor. The equivalent susceptance, which neglects harmonic current, is expressed as follows [18]. Fig. 3 Equivalent model of SVC The reactive power provided by SVC in power flow framework is expressed as The constraint on the reactive power at bus k is: 4 Multi-objective formulation for optimal setting and placement of FACTS devices The FACTS controllers like SVC and TCSC connected at the suitable location leads to interference of voltage collapse and better voltage profile. The power injection model may be a smart model for a FACTS technology because it will handle them well during a load-flow computation problem. Since this approach will not destroy the existing impedance matrix, it would be easy to implement in load-flow programs. In fact, this model is convenient and sufficient for a network with a FACTS controller. In this work, SVC and TCSC devices have been used to improve static voltage stability, decrease the real power losses and reduce the load voltage deviation. The problem for placing series and shunt FACTS controllers is developed as a multi- objective problem with the following objectives and constraints. 4.1 Objectives of optimization The main aim of this work is to determine the optimal location and setting of the SVC and TCSC devices in the power network to eliminate or minimize the risk of load voltage deviation, improve static voltage stability margin and minimize real power losses. The objectives selected are presented below. 4.1.1 Real power losses (RPL) In this section, with the help of FACTS devices, the aim is to reduce the real power loss in the transmission lines. Minimize RPL: where 4.1.2 Static voltage stability margin (SVSM) SVSM is static voltage stability margin or loading limitation of accepted index for voltage collapse evaluation. In the other words, this parameter is ratio of the loading that system can withstand without the voltage collapse occurring. These calculations are done via power system analyzing toolbox (PSAT) and it should increase to its maximum potential. This parameter is shown by λ and therefore the goal is to maximize it. λ obtained as SVSM objective is described in the equation bellow: In the equation above λ is loading limitation of the buses; PoL and QoL are system load in initial condition; PL and QL are system load at working point. In fact, λ indicates the rate of system load-ability compared to its initial load ability due to installation of the FACTS[19]. 4.1.3 Load voltage deviation (LVD) To obtain a sufficient voltage index, the voltage variation at each load bus should be made as small as possible. The load voltage variation is to be minimized as follows: where NL is the number of load buses and 4.2 Equality and inequality constraints The equality constraints represent the standard load flow equations. The inequality constraints represent the operational limits of the TCSC and SVC. Moreover, two security limits are considered in this work, namely the thermal limits of the transmission lines and the bus voltage limits, which are applied on the two last objectives only (RPL, LVD) because in the general case, the voltage collapse occurs after the security limits have been exceeded. 4.3 Implementation for optimal location of SVC and TCSC A SPMOEA is introduced to attain the most effective best compromise among the conflicting objectives mentioned above and thus solve the composite objective for the FACTS placement problem. The flowchart of the optimization strategy is presented in Fig. 4. SVSM, LVD and RPL based objective functions are calculated for each chromosome in population. Finally, at the ending of the optimization process, the best solutions of the SPMOEA are selected and compared to the literature. In general, the increasing of the SVM increases the LVD and RPL. In the other word, improvement of SVSM demolishes the LVD and RPL. This situation along with presence of FACTS devices adds more complexity to the optimization process. Hence, in order to consider all of these parameters, the multi objective approach is used to find the optimal solutions that could satisfy all of the requirements of the problem. In this algorithm, after that, the network data together with the parameters to be used in the objective fitness functions are selected. The algorithm implements the load flow program for IEEE 30-bus [20] and IEEE 118-bus [21] system to compute bus voltages before installing TCSC and SVC. In the next step, initial population of chromosomes is generated. This initial population consists of two parts, so a number of genes (bits) are related to location and others to setting. Furthermore, these chromosomes are converted from binary to decimal or, say, decoded. The setting and location of SVC and TCSC devices is calculated for each chromosome after decoding. Hence, load flow program is implemented to obtain voltage profile for each chromosome in population. The most effective chromosomes are selected as parents for next generation. Then, mutation and crossover operators are performed on these selected parents and produce the next population. This process is repeated until stopping criterion is satisfied. 5 Results and discussion The proposed approach is applied on IEEE 30-bus six generators and the IEEE 118-bus 54 generators test systems. The generators are modeled as PV buses with reactive power limits. The number of FACTSs to be installed is chosen one for each type and also the limitations are fixed at the beginning by the designer. The reactance of TCSC is considered a capacitive reactance varying continuously between 20% and 80% of the line reactance. The location of the TCSC is regarded as a discontinuous variable, wherever all transmission lines are option to be the optimal location of TCSC. Also, the SVC is regarded as a simultaneous compensator with a reactive power changing consecutive within -2 pu and 2 pu. The optimal placement of SVC is considered discreet decision variable, where all load buses are selected to be the suitable location of SVC. In this work, the optimal locating and sizing of the SVC and TCSC is performed for two multi-objective problems, considering several combinations of FACTS devices. The results of SPMOEA of the bi- and three-objective optimization problems are compared with those of the non-dominated sorting particle swarm optimization (NSPSO) in IEEE 30-bus test system [22]. Fig. 4 Flowchart of implemented optimization strategy 5.1 With two objectives (SVSM and RPL optimization) The aim of this part is to optimize the location and the size of the TCSC and SVC to maximize the SVSM and minimize the RPL. 5.1.1 IEEE 30-bus test system The system has six generators located at buses 1, 2, 5, 8, 11 and 13 and four transformers with off-nominal tap ratio in lines 6-9, 6-10, 4-12 and 27-28 [20]. The total active and reactive powers of load are 283.4 MW and 126.2 MVar, respectively. The lower voltage magnitude limits are 0.95 pu for all buses and the upper limits are 1.1 pu for generators 2, 5, 8 and 13, and 1.05 pu for the remaining buses including the reference bus 1. Case 1: Only one TCSC. The optimal location and setting of TCSC is calculated using the SPMOEA (Fig. 5). From Fig. 5, it can be concluded that the SPMOEA provides well-distributed solutions over the trade-off surface. Table 1 presents the Pareto solution of case 1 for bi-objective optimization of the SPMOEA and NSPSO methods. The maximum and minimum values of SVSM and RPL are given in Table 1 of section 1 using SPMOEA, when TCSC is placed in system, are 3.7434 pu and 0.0413 pu, respectively. Whereas the values of these parameters in NSPSO algorithm were 2.4160 pu and 0.529 pu, respectively. We tend to see that the results are much better than NSPSO by SPMOEA strategies. Fig. 5 Optimal location and size of TCSC of case 1 for IEEE 30-bus test system Case 2: Only one SVC. As mentioned earlier, the aim of the optimization is to exploit the available network adequately in accordance with the most effective location and parameters of SVC. The optimization strategy is made on two parameters: location and size. The SVC size limits are fixed at the beginning. In doing so, the SVC is considered a synchronous compensator with a reactive power changing continuously between -2 and 2 pu. The problem is formulated as bi-objective optimization considering the minimization of real power losses and the maximization of static voltage stability margin. Figure 6 depicts the Pareto-optimal solutions of the best location and size of case 2. Table 1 presents the Pareto solution of case 2 for bi-objective optimization of the SPMOEA and NSPSO methods. Furthermore, we can conclude that the placement of SVC at bus 8 with the reference set at 0.7488 pu provides the best SVSM of 3.2146. The installation of SVC at bus 9 with 0.1701 pu of reference provides the minimum RPL of 0.0522 pu. Case 3: Coordinated SVC and TCSC. The Pareto optimal solution of case 3 is presented in Fig. 7. Table 2 presents the best solution of SVSM and RPL using the SPMOEA and NSPSO algorithms for case 3. Furthermore, we can conclude that the placement coordinated SVC at bus 8 with the reference set at 0.8035 pu and TCSC between buses 25 and 27 with 0.79 pu of reference provides the best SVSM of 4.0027 pu. The installation coordinated SVC at bus 8 with the reference set at 0.1466 and TCSC between buses 27 and 28 with 0.8 pu of reference provides the minimum RPL of 0.0413 pu. Compared with the two previous cases, the case 3 gives the best SVSM. 5.1.2 IEEE 118-bus test system The system has 54 generators located at buses 1, 4, 6, 8, 10, 12, 15, 18, 19, 24, 25, 26, 27, 31, 32, 34, 36, 40, 42, 46, 49, 54, 55, 56, 59, 61, 62, 65, 66, 70, 72, 73, 74, 76, 77, 80, 85, 87, 89, 90, 91, 92, 99, 100, 103, 104, 105, 107, 111, 112, 113, 116 and ten transformers with off-nominal tap ratio in lines 1-2, 8-5, 26-25, 30-17, 38-37, 63-59, 64-61, 65-66, 68-69 and 81-80. The total system demand is 3668 MW. The lower and upper voltage limits of all buses are 0.95 pu and 1.09 pu, respectively [21]. Table 1 SPMOEA and NSPSO solutions of case 1 and case 2 for bi-objective optimization Fig. 6 Optimal location and size of SVC of case 2 for IEEE 30-bus test system Fig. 7 Optimal location and size of TCSC and SVC of case 3 for IEEE 30-bus test system Table 2 SPMOEA and NSPSO solutions of case 3 for bi-objective optimization Case 1: Only one TCSC. The optimal location and setting of TCSC is presented in Fig. 8, while used from SPMOEA. From Fig. 8, it can be concluded that the SPMOEA provides well-distributed solutions over the trade-off surface. The optimal solution of each objective and the extreme points given by SPMOEA are presented in Table 3. From Table 3, it can be concluded that the installation of a TCSC in line between buses 69 and 75 with 0.8 pu of reference provides the best SVSM of 0.8648 pu and the installation of TCSC in line between buses 69 and 77 with 0.8 pu of reference provides the minimum RPL of 0.1063 pu. Fig. 8 Optimal location and size of TCSC of case 1 for IEEE 118-bus test system Table 3 SPMOEA solutions of case 1 and case 2 for bi- objective optimization Case 2: Only one SVC. Figure 9 depicts the Pareto-optimal set of case 1. The best solution of SVSM and RPL optimized individually the SPMOEA and the solutions obtained by the proposed method are presented in Table 3. From Table 3, it can be seen that the extreme points of the Pareto front and the best solution of each function are almost identical. Furthermore, we can conclude that the placement of SVC at bus 57 with thereference set at 0.9485 pu provides the best SVSM of 0.6146 pu. The installation of SVC at bus 60 with 0.3815 pu of reference provides the minimum RPL of 0.1032 pu. Fig. 9 Optimal location and size of SVC of case 2 for IEEE 118-bus test system Case 3: Coordinated SVC and TCSC. The Pareto optimal of case 3 is presented in Fig. 10. Table 4 presents the best solution of SVSM and RPL using the SPMOEA algorithm for case 3. Furthermore, we can conclude that the placement coordinated SVC at bus 8 with the reference set at 0.8035 pu and TCSC between buses 25 and 27 with 0.79 pu of reference provides the best SVSM of 4.0027 pu. The installation coordinated SVC at bus 8 with the reference set at 0.1466 and TCSC betweenbuses 27 and 28 with 0.8 pu of reference provides the minimum RPL of 0.0413 pu. Compared with the two previous cases, the case 3 gives the best SVSM. Fig. 10 Optimal location and size of TCSC and SVC of case 3 for IEEE 118-bus test system Table 4 SPMOEA solutions of case 3 for bi-objective optimization 5.2 Three-objective state (SVSM, RPL and LVD optimization) This section is more complicated than the previous one, where three objectives are considered, namely, SVSM, RPL and LVD. The main aim is to optimize the location and the size of TCSC and SVC with maximize the SVSM and minimize the RPL and LVD. 5.2.1 IEEE 30-bus test system Case 1: Only one TCSC. Here, we can observe that placing TCSC can improve the SVSM, and RPL and LVD are reduced. Table 5 shows the results given by the SPMOEA and NSPSO methods, for the system with TCSC. Figure 11 shows the best location and setting of TCSC by the SPMOEA method. The results of Table 5 in case 1 shows that, when TCSC is located in the system, by SPMOEA the SVSM reaches to 3.7434, while the value of this parameter by NSPSO method is equal to 2.4160 pu, indicating a significant increase in this parameter when SPMOEA is used. On the other hand, the minimum loss of real power in the SPMOEA is 0.0413 pu; compared with 0.0529 pu obtained in NSPSO, this parameter also is increasingly reduced. Finally, the LVD parameter obtained by tested method in this work is 0.4279 pu while the amount of this parameter in NSPSO method is equal to 0.6008 pu. In other words, by comparing the results of the two methods described above, the superiority of SPMOEA method to NSPSO method is shown. Case 2: Only one SVC. Comparisons between static voltage stability margin and real power losses and load voltage deviation after placing SVC with an optimal solution given by the SPMOEA and NSPSO [22] methods are shown in Table 5. Figure 12 presents the best solutions for the optimal location and size of SVC. Table 5 SPMOEA and NSPSO solutions of case1 and case 2 for three-objective optimization Fig. 11 Optimal location and size of TCSC of case 1 for IEEE 30-bus test system Fig. 12 Optimal location and size of SVC of case 2 for IEEE 30-bus test system 5.2.2 IEEE 118-bus test system Three scenarios have been considered and in each scenario, SPMOEA has been implemented for finding optimal placement and setting for FACTS devices. Case 1: Only one TCSC. In case one, TCSC is employed. Results for one-type FACTS location and setting using SPMOEA are presented in Table 7. Figure 14 depicts the Pareto solution for the optimal location and size of TCSC considering the maximization of SVSM and the minimization of RPL and LVD. Case 3: Coordinated SVC and TCSC. The problem is formulated as three-objective optimization considering the minimization of RPL, LVD and the maximization of SVSM. Results for two-type FACTS (TCSC, SVC) placement using SPMOEA and NSPSO have been compared and presented in Table 6. The optimal placement and setting of SVC and TCSC of case 3 are presented in Fig. 13. Case 2: Only one SVC. The SVC is placed at different locations and it is observed that static voltage stability margin is improved and also real power losses and load voltage deviation are reduced. Table 7 shows optimal location and setting of SVC in case 2. Figure 15 indicates that the best SVSM and RPL and LVD were achieved by installation of SVC. Case 3: Simultaneous SVC and TCSC. In this case, two types of controllers simultaneously have been implemented to improve SVSM, RPL and LVD criteria.Figure 16 illustrates the convergence of three objective functions, SVSM, RPL and LVD. Consequences for two-type FACTS (SVC, TCSC) location by SPMOEA have been assessed and presented in Table 8. Table 6 SPMOEA and NSPSO solutions of case 3 for three-objective optimization Fig. 13 Optimal location and size of SVC and TCSC of case 3 for IEEE 30-bus test system Fig. 14 Optimal location and size of TCSC of case 1 for IEEE 118-bus test system Table 7 SPMOEA solutions of case 1 and case 2 for three- objective optimization Fig. 15 Optimal location and size of SVC of case 1 and 2 for IEEE 118-bus test system Fig. 16 Optimal location and size of SVC and TCSC of case 3 for IEEE 118-bus test system Table 8 SPMOEA solutions of case 3 for three-objective optimization 6 Conclusions This work conferred the appliance of strength Pareto multi-objective evolutionary algorithm to find the optimal setting and placement of SVC and TCSC devices. The design problem is developed as a nonlinear multi-objective optimization, where two different problems are considered. Firstly, the SVSM and RPL are considered two competing objectives. Then, in the second problem, the LVD target is added to the first problem. The SPMOEA is used for optimization of placement and setting of SVC and TCSC to reduce real power losses, load voltage deviation and increase the voltage stability margin. The net results are compared with those calculated by NSPSO algorithm. This comparison confirmed the usefulness of the proposed multi-objective technique. References [1] CANIZARES C A. Applications of optimization to voltage collapse analysis [C]// IEEE/Power Engineering Society Summer Meeting, IEEE Conference Proceedings. San Diego, 1998: 41-48. [2] KUNDUR P, PASERBA J, AJJARAPU V, ANDERSSON G, BOSE A, CANIZARES C A, HATZIARGYRIOU N, HILL D, STANKOVIC A, TAYLOR C, VAN-CUTSEM T, VITTAL V. Definition and classification of power system stability [J]. IEEE Trans Power Systems, 2004, 19(3): 1387-1401. [3] FAUR T Z. Effects of facts devices on dtatic voltage collapse phenomena [D]. Waterloo: Dept Elect Eng, Univ of Waterloo, 1996. [4] YORINO N, EL-ARABY E, SASAKI H, HARADA S. A new formulation for facts allocation for security enhancement against voltage collapse [J]. IEEE Trans Power Systems, 2003, 18(1): 3-10. [5] LIE T T, DENG W. Optimal flexible AC transmission systems (FACTS) devices allocation [J]. Int J Electr Power Energy Syst, 1999, 19(2): 125-134. [6] SHIN J R, KIM B S, PARK J B, LEE K Y. A new optimal routing algorithm for loss minimization and voltage stability improvement in radial power systems [J]. IEEE Trans Power Systems, 2007, 22(2): 648-657. [7] FARSANGI M M, NEZAMABADI-POUR H, LEE K Y. Multi- objective VAR planning with SVC for alarg power system using PSO and GA [C]// Proceeding of Power System Conference& Exposition. 2006: 274-279. [8] MANSOUR Y. SVCplacement using critical modes of voltage instability [J]. IEEE Trans on Power Systems, 19994, 9(2): 757-763. [9] PILOTTO L A S. Determination of needed facts controllers that increase asset utilization of power systems [J]. IEEE Trans on Power Delivery, 1997, 12(1): 364-371. [10] SARAVANAN M, SLOCHANAL S M R, VENKATESH P, PRINCE J, ABRAHAM S. Application of particle swarm optimization technique for optimal location of FACTS devices considering cost of installation and system loadability [J]. Electric Power System Research, 2007, 77(3): 276-283. [11] VERMA M K, SRIVASTAVA S C. Optimal placement of SVC for static and dynamic voltage security enhancement [J]. Int J Emerging Electric Power Systems, 2005, 2(2): 25-31. [12] SHARMA P R, DUBE A. Location of SVC and UPFC for real power loss minimization and stability enhancement in a multi machine power system using parametric approach [J]. Int J Advanced Electrical Electronics Engineering, 2012, 1(1): 34-42. [13] ESMAEILIDAHEJ A, ESMAEILI S, GOROOHI A. Optimal allocation of SVC and TCSC for improving voltage stability and reducing power system losses using hybrid binary genetic algorithm and particle swarm optimization [J]. Can J Electrical Electronics Engineering, 2012, 3(3): 54-62. [14] ABIDO M A, BAKHASHWAIN J M. Optimal VAR dispatch using a multiobjective evolutionary algorithm [J]. Electrical Power and Energy Systems, 2005, 27(1): 13-20. [15] ZITZLER E, THIELE L. An evolutionary algorithm for multiobjective optimization: the strength Pareto approach [R]. Swiss Federal Institute of Technology, TIK-Rep, No. 43, 1998. [16] TIWARI P K, SOOD Y R. An efficient approach for optimal allocation and parameters determination of TCSC with investment cost recovery under competitive power market [J]. IEEE Transactions on Power Systems, 2013, 28(3): 2475-2484. [17] SEBAA K, BOUHEDDA M, TLEMCANI A, HENINI N. Location and tuning of TCPSTs SVCs based on optimal power flow and an improved cross-entropy approach [J]. Electrical Power and Energy Systems, 2014, 54(1): 536-545. [18] REZAEI M, KARAMI A. Artificial bee colony algorithm for sloving multi-objective optimal power flow problem [J]. Electrical Power and Energy Systems, 2013, 53(1): 219-230. [19] MILANO F. PSAT Version 1. 3. 4, software and documentation [M]. 2005. [20] ALSAC O, STTOT B. Optimal load flow with steady state security [J]. IEEE Trans Power Apparatus Systems, 1974, 93(3): 745-751. [21] KALAIVANI R, KAMARAJ V. Application of stochastic algorithms for optimal location of SVC to avoid voltage instability [J]. Int J Electrical Engineering, 2012, 5(1): 611-628. [22] BENABID R, BOUDOUR M, ABIDO M A. Optimal location and setting of SVC and TCSC devices using non-dominated sorting particle swarm optimization [J]. Electric Power Systems Research, 2009, 79(12): 1668-1677. (Edited by YANG Hua) Cite this article as: Amin Safari, Mojtaba Bagheri, Hossein Shayeghi. Optimal setting and placement of FACTS devices using strength Pareto multi-objective evolutionary algorithm [J]. Journal of Central South University, 2017, 24(4): 829-839. DOI: 10.1007/s11771-017-3485-x. Received date: 2015-12-03; Accepted date: 2016-04-11 Corresponding author: Amin Safari, Assistant Professor, PhD; Tel: +98-41-34327500; E-mail: asafari1650@yahoo.com
 (1)
(1) for each individual in the outer set. The strength is commensurate to the number of individuals covered by it.
for each individual in the outer set. The strength is commensurate to the number of individuals covered by it.
 (5)
(5) (6)
(6)
 (7)
(7)
 (8)
(8)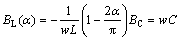 (9)
(9) (10)
(10) (11)
(11) (12)
(12) describes the conductance of the kth line; NL describes the number of the transmission lines; Vi<δi and Vj<δj are the voltages at the end buses i and j of the kth line, respectively.
describes the conductance of the kth line; NL describes the number of the transmission lines; Vi<δi and Vj<δj are the voltages at the end buses i and j of the kth line, respectively. (13)
(13) (14)
(14) (15)
(15) is the pre-specified reference value of the voltage magnitude at the kth load bus,
is the pre-specified reference value of the voltage magnitude at the kth load bus,  is usually set to 1.0 pu.
is usually set to 1.0 pu.