DOI: 10.11817/j.issn.1672-7207.2017.01.020
低复杂度的TPC自适应译码算法
韩明，张佳岩，赵洪林
(哈尔滨工业大学 通信技术研究所，黑龙江 哈尔滨，150001)
摘要：为降低TPC译码算法复杂度，提出一种新的低复杂度自适应译码算法。新算法适用于子码为扩展汉明码的TPC码，以不估计SNR的自适应译码算法为基本框架结构，利用码字可靠性特征，引入1个可用于外信息计算的简单公式，在自适应减小不可靠比特数的同时，降低外信息的计算量。研究结果表明：对于扩展汉明码(64,57,4)为子码的TPC码，新算法相比于原自适应译码算法在误码率为10-5时Eb/N0仅降低了0.05 dB，复杂度却降低约1/3，可见新算法在性能和复杂度方面实现了很好的平衡和折中。
关键词：TPC；Chase-Pyndiah译码；自适应译码；低复杂度
中图分类号：TN911.22 文献标志码：A 文章编号：1672-7207(2017)01-0141-07
A low-complexity adaptive decoding algorithm for Turbo product code
HAN Ming, ZHANG Jiayan, ZHAO Honglin
(Communication Research Center, Harbin Institute of Technology, Harbin 150001, China)
Abstract: A new efficient adaptive decoding algorithm was proposed to reduce the complexity of Turbo product code (TPC) decoding algorithm. The new algorithm was suitable for the TPCs formed by extended Hamming codes. The adaptive decoding algorithm without estimating SNR was the basic framework of the proposed algorithm and a simple formula for calculating the extrinsic information was introduced after analyzing codeword reliability. In the proposed algorithm, the least reliable bits could be reduced adaptively; meanwhile, computation of the extrinsic information should be simplified. The results show that when the extended Hamming code (64,57,4) is the subcode of TPC and the bit error rate is 10-5, the performance loss of the proposed algorithm is only 0.05 dB compared with the adaptive decoding algorithm without estimating SNR. But the complexity is decreased by about 1/3. So the proposed algorithm is an excellent balance and compromise between complexity and performance.
Keywords: Turbo product code; Chase-Pyndiah decoding; adaptive decoding; low complexity
Turbo乘积码(Turbo product code，TPC)由Turbo码延伸而来，是一种高效的信道编码方式[1]，具有很强的纠错能力，因性能接近香农极限而受到关注。目前4G LTE(long term evolution)网络已开始应用，更快的数据传输需要通信新技术的支持，TPC码也可应用于LTE中以提高系统可靠性[2-3]。TPC自提出以来，各国学者一直致力于其译码算法的研究[4-6]。PYNDIAH等[7]以Chase算法[8]为基础，提出了TPC的软输入软输出(soft input soft output, SISO)迭代译码算法，称为经典的Chase-Pyndiah算法。该算法性能优越，但复杂度较高，如何在性能和复杂度间找到最佳平衡点是必须要解决的实际问题。随着译码过程的进行，自适应改变与运算量相关的参数是一种有效的解决方法。MAHRAN等[9]首先提出了TPC自适应译码算法，通过设定与信噪比SNR有关的门限，降低了译码复杂度。LIU等[10]对自适应译码算法进行改进，使其更适合实际使用，但是该算法要对SNR进行估计，这不仅带来了相当数量的乘法运算，而且要有大量的数据才能确保估计结果相对准确。党小宇等[11]提出了不估计SNR的自适应译码算法，根据接收码字的统计特性来调整参数，使得译码复杂度降低。尽管近些年有部分学者研究了TPC译码新算法[12-13]，但自适应译码依旧是一个值得探讨的方向。本文作者以不估计SNR的自适应译码算法为基础，融入1个计算外信息的简单公式，提出自适应译码新方法。
1 TPC编码与译码
1.1 TPC编码结构
TPC码具有二维块状结构[14]，如图1所示，子码为线性系统分组码，n和k分别表示码字长度和信息位长度，其码型可以灵活选取，通常为汉明码、BCH码或RS码，相应编码的扩展码字形式也常被采用以增加纠错能力。
TPC编码简单，先对信息比特矩阵逐行编码，再将得到的矩阵逐列编码即可[15]。行列编码的先后顺序不同，不影响编码效果。理论上讲，对行和列的编码可以采用不同的编码结构和编码方式，但考虑到实际实现中的编译码复杂度，一般采用相同的编码规则来构造TPC码。
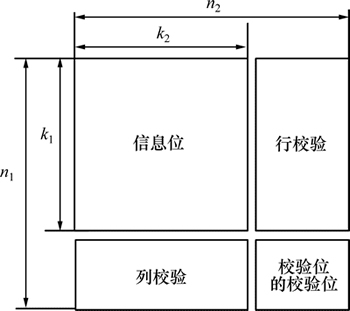
图1 TPC编码结构
Fig. 1 Structure of TPC
1.2 传统的Chase-Pyndiah译码算法
针对TPC译码，PYNDIAH等[7]提出了SISO的概念，其基本思想是：根据接收到信号的软信息R，确定p个不可靠位，从而形成q(
)个测试序列Z，然后对测试序列进行代数译码得到候选码字集合
，最后通过欧氏距离信息，在中找到似然码字D和竞争码字C，从而计算软输出和外信息。第j个码元的软输出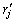
和外信息wj可以由式(1)和式(2)来表示。
(1)
(2)
式中：
为似然码字D中第j个码元；
为可靠性因子，随迭代的进行而渐渐增大。译码时一般设定迭代次数为4，此时最好的取值为0.2, 0.4, 0.6, 0.8, 1.0, 1.0, 1.0, 1.0。
Chase-Pyndiah算法的1次迭代过程如图2所示，由2个半迭代构成。图2中：W为外信息；m为半迭代次数；
为重量因子，用于调整外信息在软输入信息里所占的比重；row和col分别表示行和列。迭代结构中的软输入信息的表达式如下：
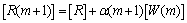(3)
开始迭代时，外信息可靠性低，取值较小，随着迭代深入，应不断增大。据前人经验，当为0, 0.2, 0.3, 0.5, 0.7, 0.9, 1.0, 1.0时，4次迭代效果最好。
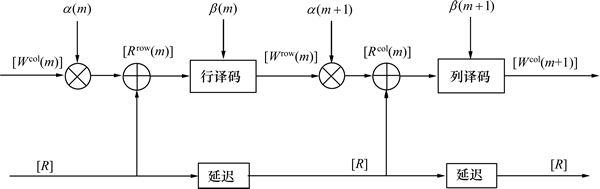
图2 Chase-Pyndiah迭代译码结构
Fig. 2 Structure of Chase-Pyndiah iterative decoder
Chase-Pyndiah算法的复杂度主要来自2方面：一方面是构造候选码字集合时大量的代数译码，另一方面是计算外信息时繁杂的算数运算[4]。对于行列编码方式相同的TPC码，以每一行(列)接收信号的译码运算量来说明复杂度：每一行(列)数据都确定p个最不可靠位，对应测试序列
个，需要进行q次代数译码，若迭代次数为IT，则构造每一行(列)的候选码字集就要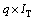
次代数译码；对于外信息的计算，先要找到行(列)中每个码元所对应的竞争码字C，若子码的码长为n，则要进行
次算术运算(主要比较和存储等相关操作)。
p对TPC译码性能有明显影响，而以上分析知算法复杂度也随p呈指数增加，故p的选择要从性能和复杂度2方面折中考虑。随译码过程进行，码字可靠性提高，合理地减小p将是简化译码算法的有效手段，而算法的复杂度则可以用代数译码(hard-decision decoding，HDD)数目和算术运算(arithmetic operation，AO)数目来衡量和评价。
1.3 不估计SNR的自适应译码算法
不估计SNR的自适应译码算法见文献[11]。子码为扩展汉明码时，首先统计与接收信号相同最小欧氏距离的候选码字数目，依据统计数据，自适应地减小不可靠比特数p，从而降低算法复杂度。其实现过程简单介绍如下。
1) 对于接收信号序列中的1个TPC码块，使用Chase-Pyndiah算法进行1次行译码。设定不可靠位数为p，每行信息译码后都会得到代数译码后的数据与软输入信息的欧氏距离
个。
2) 设定门限值A，检查每行序列的个欧氏距离中最小相同欧氏距离的个数，记为Ns。当1个TPC码块的所有行均完成译码后，统计该码块中Ns≥p+1的行数Nr，当Nr≥A时，p自动减1；否则，保持p不变。
3) 进行行列交织，按照步骤1)和2)的规则，使用已经更新过的p对码块列译码，根据译码后统计结果与门限值的关系再次对p调整。
4) 按以上3步继续进行，TPC迭代译码，p随着迭代次数的进行不停调整，输出最终译码结果。需要注意的是：为了保证译码性能，当p为1以后，不管是否满足p减1的条件，都保持p不变。
此算法采用了自适应译码的新思想，不需要进行SNR估计，不但减小了译码复杂度，而且更有利于算法的实现，但是降低复杂度方面仍然有很大的提升空间。接下来以该算法为基础，融入1个用于计算外信息的简单公式，给出新的自适应译码算法。
2 新的自适应译码算法
2.1 计算外信息的简单公式
Chase-Pyndiah算法中，不存在竞争码字C，表示代数译码后可靠性较高。若可靠，则外信息
可通过和1个可靠性参数来进行估计。这样就可以引入1个计算外信息的简单公式，见文献[16]中。因新算法中此公式至关重要，现将其推导过程介绍如下。
接收信号硬判决码字为
，其中
，经代数译码得
，其中
。若
准确性很高，则可认为
可靠，外信息可以用下式来描述。
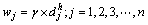(4)
其中：
为可靠性参数。
由于越可靠，越大，故可利用的可靠性来推导的表达式。
对于高斯白噪声信道下的BPSK调制，比特可靠性信息(log likelihood radio, LLR)可以用下式表示：
(5)
将此概念扩展码字上去，则的可靠性可以由下式来定义：
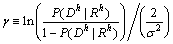(6)
若
表示与
有第二小汉明距离的码字。高信噪比时(即
时)，有
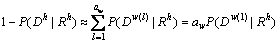(7)
因此，式(6)可以近似表达为
(8)
令
表示2个序列A和B的汉明距离。假设中可能的错误数为e，即
。在高信噪比时，可以用
来确定，若1 bit错误接收的概率为
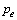，则的表达式为
(9)
由文献[17]知：对于BPSK调制来说，其误码率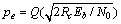
，其中
；而高信噪比时，Q函数的上边界被用来作为BPSK的误码率表达式，故式(9)又可以化为
(10)
随着时，显然有
(11)
而
(12)
故
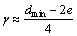(13)
这样式(4)变为
(14)
综上，对于确定的TPC码，外信息可以由e和来决定。当满足式(14)的适用条件时，只需进行1次代数译码，而省去了构造候选码字集和计算外信息的大量运算，简化了算法复杂度。
以上的推导过程都是建立在代数译码可靠这一理论基础上的，而可靠性是e (
)的函数，故可以设定1个门限
，若e＜，则认为代数译码可靠，式(14)即可使用。门限的选择与子码码型有关，应在其最大纠错能力以内，可通过软件仿真来确定，见文献[16]。
2.2 新算法译码流程
新算法以1.3中介绍的不估计SNR的自适应译码算法为基础，融入新的外信息公式，在自适应减小p的同时，简化可靠码字的外信息计算。
尽管由2.1节中推导过程可知式(14)也适用于纠多位错的BCH码或RS码，但不估计SNR的自适应译码算法是以TPC子码是扩展汉明码为前提提出的，算法中的理论和译码步骤都与扩展汉明码对应，新算法以此为基本框架，所以为方便讨论，也采用扩展汉明码作为子码，其他码型需要进一步类比分析。由于扩展汉明码只能纠正全部一位错误和部分2位错误[18]，若门限过低，则必然影响译码性能，综合考虑纠错能力，可将门限设定为1，也就是说，对于每一行(列)的外信息计算，若原码字正确，则利用新公式，否则使用传统算法。需要注意的是，译码正确意味着
，此时式(14)简化为
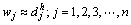(15)
以码块的1次行译码为例来介绍新算法，其基本流程如图3所示，具体步骤如下。
1) 硬判决操作。接收到的TPC码块信号，每行均进行硬判决，第i行的硬判决码字可记为。
2) 代数译码。对硬判决后的序列逐行进行代数译码，第i行代数译码得到。
3) 错误检测。计算和之间的汉明距离
，若=0，则表明已经正确，码字可靠，使用公式(15)来计算外信息，同时调整
，若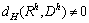
，则使用原算法。需要注意的是：因为可能存在3个错误，这里不应以
为依据来改变
。
4) 自适应调整p。根据Nr与门限A的关系来调整不可靠比特数p。
图3 新的自适应译码算法流程图
Fig. 3 Flow chart of new adaptive decoding algorithm
3 算法仿真分析
为证明新算法在性能和复杂度方面的优良特性，使用Matlab软件对传统算法、1.3节的自适应译码算法和2.2节的新算法分别进行仿真和对比分析。TPC子码设定为(64,57,4)的扩展汉明码，采用BPSK调制方式，信息在加性高斯白噪声信道中传输，不可靠比特初始值设为p=4，迭代4次。另外，如1.2节中分析，算法复杂度可用代数译码数目和算术运算数目来衡量和评价。
对于不估计SNR的自适应译码算法，设定的门限越小，复杂度越低，但是性能也随之变差，若性能损失太大，则得不偿失。不同门限的算法译码性能如图4所示。以误码率为10-5为例，A=56时和A=48时，分别损失了约0.1 dB和约0.5 dB的性能；而A=40时，性能损失过大，不宜选取。
图4 原自适应译码算法性能
Fig. 4 Performance of original adaptive decoding algorithm
为保证译码性能，设定A=56，对新算法进行仿 真，性能和复杂度如图5~7所示，其中归一化代数译码和算术运算的运算量分别用RHDD和RAO表示。在误码率为10-5处，相比于传统算法，新算法Eb/N0仅降低了约0.15 dB，但是代数译码运算量降低了约60%，算数运算量降低了约70%，总体复杂度在传统算法的40%以下；相比于原自适应译码算法，新算法Eb/N0仅降低了0.05 dB，算法复杂度却降低了约1/3，可以在很大程度上减少译码延时。
图5 各译码算法性能
Fig. 5 Performance of different decoding algorithms
图6 代数译码复杂度对比
Fig. 6 Comparison of HDD’s complexity
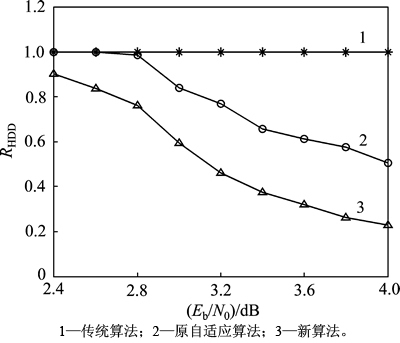
图7 算术运算复杂度对比
Fig. 7 Comparison of OA’s complexity
从译码流程和仿真结果来看：由于新算法对可靠码字都使用式(15)进行了相同处理，而忽略了各码元差异性，使得外信息矩阵较传统方法有所变化，虽变化不大，但当不可靠比特数减小时，这种变化的影响已逐渐表现出来，导致性能稍有下降。但是，新算法根据译码程度来减少不可靠比特数，并对可靠码字只进行1次代数译码，而未进行复杂的候选码字集构造和外信息计算等操作，简化了运算。综合分析，新算法尽管性能略有降低，但极大地降低了译码复杂度，优势明显。
4 结论
1) 在分析传统TPC译码复杂度来源的基础上，介绍了不估计SNR的自适应译码算法，并以此算法为基础，引入1个用于外信息计算的简单公式，提出了新的自适应译码算法，实现不可靠比特数和外信息计算的同步简化。通过与原自适应算法对比，新算法以性能的略微降低为代价，却使复杂度大幅下降，更利于硬件实现。
2) 由于新算法以不估计SNR的自适应译码算法为基本框架，而原算法是在子码为扩展汉明码的前提下提出的，这限制了新算法的适用范围，针对BCH码、RS码等码型的特点，将新算法扩展到更为一般的TPC码将是下一步研究的方向。
参考文献：
[1] MUKHTAR H, AL-DWEIK A, AL-MUALLA M, et al. Adaptive hybrid ARQ system using Turbo product codes with hard/soft decoding[J]. IEEE Communications Letters, 2013, 17(11): 2132-2135.
[2] CAO Jin, MA Maode, LI Hui, et al. A survey on security aspects for LTE and LTE-A networks[J]. IEEE Communications Surveys & Tutorials, 2014, 16(1): 283-302.
[3] ZHANG Xia, ZHANG Peijian, JIANG Wei, et al. The analysis of coded overlapped time division multiplexing system[C]// IEEE 3rd International Conference on Broadband Network and Multimedia Technology (IC-BNMT). Beijing, China, 2010: 488-494.
[4] PYNDIAH R, COMBELLES P, ADDE P. A very low complexity block Turbo decoder for product codes[C]// IEEE Global Telecommunications Conference, Communications: The Key to Global Prosperity. London, UK, 1996: 101-105.
[5] ARGON C, MCLAUGHLIN S W. A parallel decoder for low latency decoding of Turbo product codes[J]. IEEE Communications Letters, 2002, 6(2): 70-72.
[6] 董政, 巩克现, 葛临东. 低复杂度和低译码时延 TPC 迭代译码算法[J]. 四川大学学报(工程科学版), 2012, 44(2): 122-129.
DONG Zheng, GONG Kexian, GE Lindong. A low complexity and low latency TPC Iterative Decoding Algorithm[J]. Journal of Sichuan University (Engineering Science Edition), 2012, 44(2): 122-129.
[7] PYNDIAH R, GLAVIEUX A, PICART A, et al. Near optimum decoding of product codes[C]// IEEE Global Telecommunications Conference. San Francisco, CA, 1994: 339-343.
[8] CHASE D. Class of algorithms for decoding block codes with channel measurement information[J]. IEEE Transactions on Information Theory, 1972, 18(1): 170-182.
[9] MAHRAN A, BENAISSA M. Adaptive Chase algorithm for block Turbo codes[J]. Electronics Letters, 2003, 39(7): 617-619.
[10] LIU Xingcheng, WANG Kang. Adaptive SNR estimation based decoding algorithm for block Turbo codes[C]// IEEE Fourth International Conference on Communications and Networking in China (CHINACOM). Xi’an, China, 2009: 1-6.
[11] 党小宇, 陶静, 虞湘宾, 等. 一种低复杂度 Turbo 乘积码自适应Chase译码算法[J]. 电子与信息学报, 2014, 36(3): 739-743.
DANG Xiaoyu, TAO Jing, YU Xiangbin, et al. A low- complexity adaptive Chase decoding algorithm for Turbo product code[J]. Journal of Electronics & Information Technology, 2014, 36(3): 739-743.
[12] AL-DWEIK A, GOFF S L, SHARIF B. A hybrid decoder for block Turbo codes[J]. IEEE Transactions on Communications, 2009, 57(5): 1229-1232.
[13] SUN W C, CHEN Y M, WENG C Y, et al. An efficient implementation of the distance-based decoding for block Turbo codes[C]// IEEE 8th International ICST Conference on Communications and Networking in China (CHINACOM). Guilin, China, 2013: 675-679.
[14] AL-DWEIK A J, SHARIF B S. Non-sequential decoding algorithm for hard iterative Turbo product codes[J]. IEEE Transactions on Communications, 2009, 57(6): 1545-1549.
[15] CHO J, SUNG W. Reduced complexity Chase-Pyndiah decoding algorithm for Turbo product codes[C]// IEEE Workshop on Signal Processing Systems (SiPS). Beirut, Lebanon, 2011: 210-215.
[16] LU P Y, LU E H, CHEN T C. An efficient hybrid decoder for block turbo codes[J]. IEEE Communications Letters, 2014, 18(12): 2077-2080.
[17] LIN S, COSTELLO D J. 差错控制编码[M]. 2版. 晏坚, 何元智, 潘亚汉, 等译. 北京: 机械工业出版社, 2007: 4-6.
LIN S, COSTELLO D J. Error control coding[M]. 2nd ed. YAN Jian, HE Yuanzhi, PAN Yahan, et al, trans. Beijing: China Machine Press, 2007: 4-6.
[18] AL-DWEIK A J, SHARIF B S. Closed-chains error correction technique for Turbo product codes[J]. IEEE Transactions on Communications, 2011, 59(3): 632-638.
(编辑 杨幼平)
收稿日期：2016-01-25；修回日期：2016-03-20
基金项目(Foundation item)：国家科技重大专项(2012ZX03003011-004) (Project(2012ZX03003011-044) supported by the Major Program of the National Science and Technology)
通信作者：赵洪林，教授，博士生导师，从事宽带抗干扰通信技术研究；E-mail: hlzhao@hit.edu.cn
