同辊径异步轧制金属薄带最小厚度的理论分析
来源期刊:中国有色金属学报(英文版)2016年第2期
论文作者:刘鑫 刘相华 宋孟 孙祥坤 刘立忠
文章页码:501 - 507
关键词:最小厚度;金属薄带;质量守恒定律;异步轧制
Key words:minimum thickness; metal foil; law of mass conservation; asymmetric rolling
摘 要:提出一种同辊径异步轧制过程中计算金属薄带最小厚度的新方法,其要点是联解采利柯夫轧制压力公式和修正后的希区柯克轧辊压扁公式,同时为了避免极薄带轧制过程中弹性变形对秒流量的影响,采用质量守恒定律计算接触弧长中前滑区、后滑区和搓轧区的比例,推导出用于计算异步轧制最小厚度方程。通过异步轧制实验研究304不锈钢在异速比为1.05、1.15和1.30条件下可获得的金属薄带最小厚度值,并与理论计算值进行对比,结果表明,最小厚度的实验值与理论计算结果吻合较好,验证了异步轧制最小厚度方程的正确性。
Abstract: A novel approach is proposed for computing the minimum thickness of a metal foil that can be achieved by asymmetric rolling using rolls with identical diameter. This approach is based on simultaneously solving Tselikov equation for the rolling pressure and the modified Hitchcock equation for the roller flattening. To minimize the effect of the elastic deformation on the equal flow per second during the ultrathin foil rolling process, the law of conservation of mass was employed to compute the proportions of the forward slip, backward slip, and the cross shear zones in the contact arc, and then a formula was derived for computing the minimum thickness for asymmetric rolling. Experiment was conducted to find the foil minimum thickness for 304 steel by asymmetric rolling under the asymmetry ratios of 1.05, 1.15 and 1.30. The experimental results are in good agreement with the calculated ones. It was validated that the proposed formula can be used to calculate the foil minimum thickness under the asymmetric rolling condition.
Trans. Nonferrous Met. Soc. China 26(2016) 501-507
Xin LIU1, Xiang-hua LIU1,2, Meng SONG1, Xiang-kun SUN1, Li-zhong LIU3
1. State Key Laboratory of Rolling and Automation, Northeastern University, Shenyang 110819, China;
2. Research Institute of Science and Technology, Northeastern University, Shenyang 110819, China;
3. School of Materials and Metallurgy, Northeastern University, Shenyang 110819, China
Received 10 March 2015; accepted 3 December 2015
Abstract: A novel approach is proposed for computing the minimum thickness of a metal foil that can be achieved by asymmetric rolling using rolls with identical diameter. This approach is based on simultaneously solving Tselikov equation for the rolling pressure and the modified Hitchcock equation for the roller flattening. To minimize the effect of the elastic deformation on the equal flow per second during the ultrathin foil rolling process, the law of conservation of mass was employed to compute the proportions of the forward slip, backward slip, and the cross shear zones in the contact arc, and then a formula was derived for computing the minimum thickness for asymmetric rolling. Experiment was conducted to find the foil minimum thickness for 304 steel by asymmetric rolling under the asymmetry ratios of 1.05, 1.15 and 1.30. The experimental results are in good agreement with the calculated ones. It was validated that the proposed formula can be used to calculate the foil minimum thickness under the asymmetric rolling condition.
Key words: minimum thickness; metal foil; law of mass conservation; asymmetric rolling
1 Introduction
In recent years, the demand for micro- electromechanical systems (MEMS) products has been increasing. The development of novel micro- manufacturing technologies is receiving much attention [1,2]. The application of these new manufacturing technologies also extends to ultrathin foils [3]. With the development of the micro-forming technology [4-6], it is necessary to make the foils to be thinner and thinner, at the same time to maintain their excellent mechanical properties [7] and physical properties [8].
Asymmetric rolling offers the advantage of a reduced roll force and allows to improve the mechanical properties of products. For instance, ZUO et al [9] utilized this rolling technique and acquired a pure aluminum sheet with a grain size of 500 nm. WRONSKI et al [10,11] studied the grain refinement in 6061 aluminum alloys under asymmetric rolling conditions. LIU and KAWALLA [12] found that asymmetric rolling yields a greater recrystallization volume fraction and a smaller average grain size in the central layer of austenitic steel than symmetric rolling.
In traditional rolling processes, the thickness of a foil cannot be reduced below the theoretical minimum rolling thickness [13,14], not even at the expense of a greater roll force or additional rolling passes. But asymmetric rolling allows to break the limit of the traditionally achievable minimum thickness, thus making it possible to produce thinner rolled foils.
However, the theoretical determination of the possible minimum rolling thickness (PMRT) achievable by asymmetric rolling is still an unsolved problem. Compared to symmetric rolling, several experiments have demonstrated that a thinner metal foil can be achieved by asymmetric rolling [13]. YU et al [14] produced a copper foil with a thickness of only 0.005 mm by asymmetric rolling, which is considerably lower than the PMRT limit for symmetric rolling. TANG et al [13,15] later proposed an implicit form of a PMRT equation for asymmetric rolling based on the Stone formula (i.e., the rolling process was treated as a plane upsetting process). However, this formula was derived on the premise that the length of the forward slip zone is equal to that of the backward slip zone, which is not the case during the real rolling process because the stress distribution in the contact arc is much more complicated when considering the cross shear zone. In general, so far, there are very few studies on the PMRT achievable by asymmetric rolling.
Studies on the neutral angle and the forward/backward slip during the rolling process are mainly based on the law of equal volume flow per second in traditional rolling theory [16]. However, under PMRT conditions, only elastic deformation occurs in the deformed zone between the roll and the foil. Therefore, in this case, the law of equal volume flow per second is not applicable due to the elastic change in volume.
This study aimed at establishing a new PMRT equation which is more suitable to describe the characteristics of asymmetric rolling. This novel equation for calculating the minimum asymmetric rolling thickness (MART equation) was deduced from the static equilibrium equation and the law of conservation of mass.
2 Theoretical considerations
2.1 Derivation of PMRT for asymmetric rolling
The stress state of the deformation region is different when comparing the asymmetric and the symmetric rolling process. A cross shear zone occurs in the rolling area during the asymmetric rolling process, and the shear stress in this zone leads to a significant reduction of the hydrostatic pressure, which is the key factor that allows to break the PMRT limit of the symmetric rolling process. In order to better understand the differences between these two rolling processes, the contact deformation region is divided into several parts: for the symmetric rolling process, the division is shown in Fig. 1(a), and for the asymmetric rolling process, the division is shown in Fig. 1(b).

Fig. 1 Comparison of contact deformation regions for symmetric and asymmetric rolling
In Fig. 1(a), v is the linear velocity of the rolls in the case of symmetric rolling. The contact region is divided into the forward slip zone (i.e., F) and the backward slip zone (i.e., B). The friction on the upper and the lower surfaces is considered to be equivalent. In the symmetric rolling process, the vertical compressive stress is the highest around the neutral point, and the peak value of the contact pressure appears here, which is not conducive to further foil thinning.
For asymmetric rolling, since the velocities of the upper and the lower rolls are different, the contact region must be divided into three parts: the forward slip zone, the cross shear zone (i.e., C) and the backward slip zone, as shown in Fig. 1(b). In the cross shear zone, the friction vectors for the upper and the lower surfaces are pointing in the opposite direction, resulting in a state of strong shear stress in the foil, which allows the stress to reach the yield point. When comparing asymmetric and symmetric rolling, the forward slip zone and the backward slip zone are similar. The pressure distributions for both the forward slip zone and the backward slip zone are derived from Tselikov formula. If the tension is ignored, the formulae can be expressed as follows:
 (Forward slip zone) (1)
(Forward slip zone) (1)
 (Backward slip zone) (2)
(Backward slip zone) (2)
with

where pb and pf refer to the rolling pressures in the backward slip and the forward slip zones, respectively; K is the plane deformation resistance; hx is the foil thickness at any location of the contact arc; H is the foil thickness at the entrance; h is the foil thickness at the exit; l is the length of the contact arc; μ is the friction coefficient; and Δhp is the difference in thickness, i.e., Δhp=H-h. Under PMRT conditions, the elastic deformation of the rolls and the metal foil can no longer be ignored. The pressure distribution along the contact arc in the cross shear zone can be approximated as a straight line, and the following equation can be deduced from Fig. 2:
 (3)
(3)
Figure 2 shows the distribution of the rolling pressure along the contact arc for asymmetric rolling. The lengths of the contact region, the backward slip zone, the cross shear zone and the forward slip zone are denoted as l, λBl, ζ l and λFl, respectively.

Fig. 2 Pressure distribution for asymmetric rolling process
Then, the mean rolling pressure  can be expressed as
can be expressed as
 (4)
(4)
Several phenomena, e.g., the elastic flattening of the work roll and the elastic recovery of the foil during the rolling process, cannot be ignored, and therefore the Hitchcock formula must be modified as follows:

 (5)
(5)
where l′ is the contact arc length when considering the elastic deformation of the foil and the work roll, E1 and E2 are the elastic moduli of the work roll and foil, respectively, γ1 and γ2 are the Poisson ratios of the work roll and foil, respectively, and R is the radius of the work roll. Under PMRT conditions, the entry thickness of the foil is hmin, and the exit thickness is also hmin. Therefore, the plastic deformation Δhp is equal to zero.
Substituting Eqs. (1-3) and Eq. (5) into Eq. (4) and then calculating the limit for Δhp→0 yield the following MART equation:
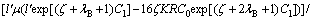

 (6)
(6)
where  ,
,  , and h is the foil thickness.
, and h is the foil thickness.
2.2 Determination of neutral angle and contact angle in asymmetric rolling process
The proportion of elastic deformation is large under PMRT conditions, and the elastic deformation will lead to a change in volume. Therefore, the formulae for calculating the neutral angle deduced from the law of equal volume flow per second are no longer applicable. Thus, the proportions of the forward slip zone, the backward slip zone and the cross shear zone with respect to the length of the contact arc had to be derived from the law of mass conservation, assuming that the mass flow through each cross section of the metal foil per second is constant.
Figure 3 illustrates the deformation zones in the asymmetric rolling process, considering both the elastic deformation of the roll and the foil. vf and vs are the linear velocities of the fast and slow rolls in the asymmetric rolling process, respectively; r1 and r2 are the neutral angles for the fast and slow rolls; R′ is the equivalent radius of the work roll when considering the elastic flattening; Δ2 is the elastic deformation of the foil, and hr1 and hr2 are the foil thicknesses at r1 and r2 of the contact arc. Δ2 is then given by
 (7)
(7)
where q refers to the rolling pressure. Considering the geometry of the setup, the deformed zone of the foil can be divided into a left interval ranging from 0 to -α and a right interval ranging from 0 to +α. If the foil thickness is higher than the minimum value hmin, the entry thickness is denoted as hM, and the exit thickness is denoted as hout, which is equal to the sum of the actual roll gap hs after elastic deformation and the elastic recovery of the foil 2Δ2, i.e., hout=hs+2Δ2. In this case, as shown in Fig. 3, |-α| ≠ |+α|. In contrast, under PMRT conditions, |-α| = |+α|.

Fig. 3 Schematic illustration of deformation regions in asymmetric rolling process
The mass flow M0 into the cross-sectional area of the mill entrance per unit time is assumed to be given by
M0=ρ0hMv0 (8)
where ρ0 and v0 are the density and velocity of the foil at the entrance, respectively. Here, the bulk modulus k is introduced. The density variable ρ can be obtained by reverting to the definition of the bulk modulus:
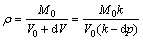 (9)
(9)
where V0 is the volume of the foil at the entrance, dV denotes the decrease in volume, and dp is the compressive stress increment of the foil.
Based on the geometry of the setup, the strain at the neutral angle of the slow roll can be calculated as follows:

 (10)
(10)
Under PMRT conditions, the contact arc is geometrically symmetrical, i.e., hM=hout=hmin. The following formulae can thus be obtained:
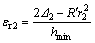 (11)
(11)
dp=E2dεr2 (12)
where dεr2 is the strain increment at the neutral angle of the slow roll.
For the left interval, under PMRT conditions, the neutral angle r2 of the slow roll can be deduced from Eqs. (7-12), resulting in

 (13)
(13)
Similarly, for the left interval, the neutral angle r1 of the fast roll can be calculated as follows:
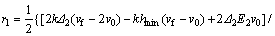
 (14)
(14)
The contact angle α can be obtained by considering the geometry of the setup.
 (15)
(15)
Based on these derivations, the proportions of the forward slip zone, the cross shear zone and the backward slip zone within the contact arc can now be deduced.
The proportion of the cross shear zone ζ is given by
 (16)
(16)
The proportion of the backward slip zone λB is given by
 (17)
(17)
And the proportion of the forward slip zone λF is given by
λF=1-ζ-λB (18)
2.3 Prediction of effect of different parameters on PMRT value
The effect of different influence factors on the PMRT value can be assessed on the basis of the above MART equation.
Figure 4(a) shows the calculated PMRT values for pure copper and 304 stainless steel as a function of the asymmetry ratio, which reflects the effect of the type of the foil material on the PMRT of the metal foil. The yield stress was set to 74 MPa for pure copper and 210 MPa for 304 stainless steel. It can be concluded that, ceteris paribus, using a material with a lower yield stress (copper) results in a smaller foil thickness.
The results presented in Fig. 4(b) were calculated based on the following assumptions: 1) the proportions of the forward slip, the backward slip and the cross shear zones were assumed to be constant for the same asymmetry ratio; 2) the roll force was fixed at 50 kN; 3) μ=0.12, K=243 MPa (for 304 stainless steel). According to the results, the smaller the roll radius, the thinner the PMRT of the metal foil. Furthermore, with increasing asymmetry ratio, the decline rate of the PMRT curve is reduced as the roll radius decreases.
For the calculations presented in Fig. 4(c), the following conditions were assumed: again, the proportions of the forward slip, the backward slip and the cross shear zones were assumed to be constant for a fixed asymmetry ratio; the roll force was fixed at 50 kN and K at 243 MPa (for 304 stainless steel). The calculation results indicate that the PMRT of the metal foil is proportional to the friction coefficient.
3 Experimental verification
3.1 Experimental procedure
Rolling experiments were performed in order to verify the theoretical PMRT limit for asymmetric rolling. A four-high pilot cold mill was used for the experiments. The specifications of the mill are listed in Table 1.
For the experiments, 304 stainless steel was selected as the metal foil material. The initial thickness of the foil was 100 μm. The stainless steel was annealed at 1050 °C for 180 s. The annealing was conducted in an OTF-1200X-100 tube furnace, with argon used as protective gas to prevent the oxidation of the foil.

Fig. 4 Effect of different influence factors on calculated PMRT value
Table 1 Specifications of four-high pilot cold mill used in experiments

Uniaxial tensile strength tests were conducted on an INSTRON-5969 stretcher to measure the yield stress of the test materials.
The technical parameters used in the experiments and calculations are listed in Table 2.
Table 2 Parameters used in experiments and calculations

In the experiments, if the thickness of the foil did not change under the maximum roll force in three consecutive rolling passes, then this thickness was considered the PMRT of the foil. The thickness of the foil was then measured using an Axio Imager M2m metallographic microscope, which yielded more precise experimental results.
3.2 Comparison of experimental and theoretical PMRT values
Rolling experiments were performed in order to validate the MART equation. Figure 5 shows the PMRT of the 304 stainless steel foil as measured using the Axio Imager M2m metallographic microscope.

Fig. 5 Foil thickness measured using metallographic microscope
In Fig. 6, the PMRT values obtained through the experiments are compared with the PMRT values calculated using the MART equation. It can be seen that they are in good agreement although the calculated PMRT values are slightly lower at each asymmetry ratio. For example, for an asymmetry ratio of 1.15, the experimental PMRT value is 45 μm, whereas the value calculated using the MART equation is only 38 μm, which corresponds to a deviation of 15.6%. During the rolling of ultrathin foils, the edges of the upper and lower working rollers come in elastic contact with each other, resulting in a roll force acting on the workpiece which is lower than the total roll force. This might be one of the reasons why the PMRT value obtained through the MART equation is lower than the experimental value.

Fig. 6 Comparison of calculated and experimental PMRT values
4 Conclusions
1) The MART equation for predicting the minimum thickness achievable by asymmetric rolling was deduced based on Tselikov formula and a modified Hitchcock formula.
2) A new equation for calculating the neutral angle within the contact arc was determined based on the law of the conservation of mass, and the proportions of the forward slip, the backward slip and the cross shear zones were obtained.
3) The MART equation predicts that the PMRT value in asymmetrical rolling decreases as the asymmetry ratio increases. The material strength, the roll diameter and the friction coefficient also affect the PMRT value.
4) The calculated PMRT values from the MART equation are in good agreement with the experimental results.
References
[1] LONGTIN R, HACK E, NEUENSCHWANDER J, JANCZAK- RUSCH J. Benign joining of ultrafine grained aerospace aluminum alloys using nanotechnology [J]. Advanced Materials, 2011, 23(48): 5812-5816.
[2] FU M W, CHAN W L. A review on the state-of-the-art microforming technologies [J]. International Journal of Advanced Manufacturing Technology, 2013, 67(9-12): 2411-2437.
[3] YU Hai-liang, LU Cheng, TIEU A K, GODBOLE A, SU Li-hong, SUN Yong, LIU Mao, TANG De-lin, KONG C. Fabrication of ultra-thin nanostructured bimetallic foils by accumulative roll bonding and asymmetric rolling [J]. Scientific Reports, 2013, 3: 2373.
[4] ZHENG Qiu, SHIMIZU T, SHIRATORI T, YANG Ming. Tensile properties and constitutive model of ultrathin pure titanium foils at elevated temperatures in microforming assisted by resistance heating method [J]. Materials & Design, 2014, 63: 389-397.
[5] EGERER E, ENGEL U. Process characterization and material flow in microforming at elevated temperatures [J]. Journal of Manufacturing Processes, 2004, 6(1): 1-6.
[6] HOSSAIN A M, HONG S T, PARK K Y, NA Y S. Microforming of superplastic 5083 aluminum alloy [J]. Transactions of Nonferrous Metals Society of China, 2012, 22: 656-660.
[7] COTTRINO S,  D, MAIRE E. Mechanical properties of crumpled aluminum foils [J]. Acta Materialia, 2014, 81: 98-110.
D, MAIRE E. Mechanical properties of crumpled aluminum foils [J]. Acta Materialia, 2014, 81: 98-110.
[8] MOSTAAN H, SHAMANIAN M, MONIRVAGHEFI S M, BEHJATI P, SZPUNAR J A, SHERAFATI J. Electron beam assisted joining of nanograin-sized Fe-Co-V magnetic foils: Study and optimization of magnetic properties of weld joints [J]. Vacuum, 2014, 109: 148-156.
[9] ZUO Fang-qing, JIANG Jian-hua, SHAN Ai-dang, FANG Jian-min, ZHANG Xing-yao. Shear deformation and grain refinement in pure Al by asymmetric rolling [J]. Transactions of Nonferrous Metals Society of China, 2008, 18(4): 774-777.
[10] WRONSKI S, BACROIX B. Microstructure evolution and grain refinement in asymmetrically rolled aluminum [J]. Acta Materialia, 2014, 76: 404-412.
[11] WRONSKI S, GHILIANU B, CHAUVEAU T, BACROIX B. Analysis of textures heterogeneity in cold and warm asymmetrically rolled aluminum [J]. Materials Characterization, 2011, 62(1): 22-34.
[12] LIU Jie, KAWALLA R. Influence of asymmetric hot rolling on microstructure and rolling force with austenitic steel [J]. Transactions of Nonferrous Metals Society of China, 2012, 22(3): 504-511.
[13] TANG De-lin, LIU Xiang-hua, SONG Meng, YU Hai-liang. Experimental and theoretical study on minimum achievable foil thickness during asymmetric rolling [J]. Plos One, 2014, 9(9): 1-12.
[14] YU Jiu-ming, JIA Guang-feng, ZHU Quan. The deformation characteristics in cross shear cold rolling of ultra-thin strip and the theory of “elastic stopper” [J]. Journal of Northeast Institute of Technology, 1982, 32(3): 17-27. (in Chinese)
[15] TANG De-lin, LIU Xiang-hua, LI Xiang-yu, PENG Liang-gui. Permissible minimum thickness in asymmetrical cold rolling [J]. Journal of Iron and Steel Research International, 2013, 20(11): 21-26.
[16] MA Dong-qing, WU Long-hua, ZHAO Lin-chun. Formula for characteristic angle and asynchronous region length of asynchronous rolling [J]. Journal of Iron and Steel Research, 1983, 3: 43-51. (in Chinese).
刘 鑫1,刘相华1,2,宋 孟1,孙祥坤1,刘立忠3
1. 东北大学 轧制技术及连轧自动化国家重点实验室,沈阳 110819;
2. 东北大学 研究院,沈阳 110819;
3. 东北大学 材料与冶金学院,沈阳 110819
摘 要:提出一种同辊径异步轧制过程中计算金属薄带最小厚度的新方法,其要点是联解采利柯夫轧制压力公式和修正后的希区柯克轧辊压扁公式,同时为了避免极薄带轧制过程中弹性变形对秒流量的影响,采用质量守恒定律计算接触弧长中前滑区、后滑区和搓轧区的比例,推导出用于计算异步轧制最小厚度方程。通过异步轧制实验研究304不锈钢在异速比为1.05、1.15和1.30条件下可获得的金属薄带最小厚度值,并与理论计算值进行对比,结果表明,最小厚度的实验值与理论计算结果吻合较好,验证了异步轧制最小厚度方程的正确性。
关键词:最小厚度;金属薄带;质量守恒定律;异步轧制
(Edited by Yun-bin HE)
Foundation item: Projects (51374069, U1460107) supported by the National Natural Science Foundation of China
Corresponding author: Xiang-hua LIU; Tel: +86-24-83682273; E-mail: liuxh@mail.neu.edu.cn
DOI: 10.1016/S1003-6326(16)64138-9

