
DOI: 10.11817/j.issn.1672-7207.2020.04.013
可重复使用运载火箭一子级垂直回收有限时间滑模控制
李晓栋,廖宇新,廖俊,罗世彬
(中南大学 航空航天学院,湖南 长沙,410083)
摘要:针对可重复使用运载火箭一子级在垂直回收过程无动力减速段的姿态控制问题,提出一种基于有限时间扩张状态观测器和改进超螺旋算法的积分终端滑模控制方法。首先,基于火箭一子级绕质心运动模型,将含有模型不确定和外部扰动的姿态跟踪控制问题转化为含总扰动的二阶系统有限时间控制问题;其次,采用有限时间扩张状态观测器对系统不可测量状态量和总扰动进行估计,进一步将状态量估计值引入积分终端滑模面,基于总扰动估计值和改进超螺旋算法设计改进超螺旋积分终端滑模控制器;最后,利用Lyapunov理论证明闭环系统有限时间稳定。研究结果表明:该控制方法能够实现可重复使用运载火箭一子级姿态的准确快速跟踪并具有良好的鲁棒性。
关键词:可重复使用运载火箭;有限时间扩张状态观测器(FTESO);积分终端滑模控制;改进超螺旋算法;有限时间收敛
中图分类号:V448.2 文献标志码:文献标识码:A 开放科学(资源服务)标识码(OSID)
文章编号:1672-7207(2020)04-0979-10
Finite-time sliding mode control for vertical recovery of the first-stage of reusable rocket
LI Xiaodong, LIAO Yuxin, LIAO Jun, LUO Shibin
(School of Aeronautics and Astronautics, Central South University, Changsha 410083, China)
Abstract: An integral terminal sliding mode control method based on finite-time extended state observer(FTESO) and modified super-twisting algorithm was proposed for attitude control problem of the first-stage of reusable rocket in unpowered deceleration phase of vertical recovery process. Firstly, based on the model of rotational motion, the attitude tracking control problem with model uncertainties and external disturbances was transformed into a finite-time control problem for the second order system with the lumped disturbance. Secondly, the FTESO was used to estimate the unmeasurable states and the lumped disturbance, and the estimations of unmeasurable states were introduced into the integral terminal sliding mode surface. Then, the modified super-twisting integral terminal sliding mode controller was designed by combining the estimations of lumped disturbance and the modified super-twisting algorithm. Finally, the finite-time stability of the closed-loop system was proved based on the Lyapunov stability theory. The results show that the proposed control method can achieve accurate and fast tracking of the first-stage of reusable rocket attitude and has good robustness.
Key words: reusable rocket; finite-time extended state observer(FTESO); integral terminal sliding mode control; modified super-twisting algorithm; finite-time convergence
可重复使用运载器(reusable launch vehicle, RLV)是指在完成发射任务后全部或部分返回着陆,经过检修维护和燃料加注后,可再次执行发射任务的一类运载器[1]。相对于一次性运载火箭而言,可重复使用运载火箭一子级(first-stage of reusable rocket, FRR)作为一类RLV,可通过多次执行助推和回收任务来降低火箭发射成本[2],因此,受到业界广泛关注。SpaceX公司的“猎鹰-9”运载火箭成功进行了多次一子级垂直回收和复用飞行,掀起了业界对FRR回收控制的研究热潮。由于FRR垂直回收过程空域大、速域广、飞行环境多变,使其本身多变量、非线性的系统又受到强烈的内外扰动和不确定性,这对控制系统的稳定性、鲁棒性和控制精度提出了更高的要求。面对如此复杂的非线性控制问题,一般的线性控制方法无法满足高精度、强鲁棒等控制需求。近年来,动态面控制[3]、自适应广义预测控制[4]、自适应反步控制[5]、滑模控制等非线性控制方法被应用于RLV飞行控制问题研究。其中,滑模控制对模型不确定和外部扰动具有较强的鲁棒性,被广泛应用于RLV的再入姿态控制。与线性滑模控制的渐进稳定相比,终端滑模(terminal sliding mode,TSM)控制不仅使系统有限时间稳定,而且具有更强的抗干扰能力[6]。文献[7]针对高超声速飞行器再入姿态控制问题,设计了终端滑模控制器(TSM controller,TSMC),保证系统有限时间趋于稳定,实现对期望值准确、快速的跟踪。文献[8]提出一种快速终端滑模控制器(fast TSMC,FTSMC),进一步减小了有限时间收敛上界。然而,TSMC和FTSMC都存在状态量的负指数项,可能会引发奇异性问题,导致系统在奇异区域输出的控制量趋于无穷大。文献[9]通过在奇异区域把终端滑模面切换成线性滑模面来避免奇异性。文献[10]通过设计非奇异快速终端滑模控制器(singularity-free FTSMC,SFTSMC),直接克服了控制器的奇异性问题。文献[11]提出的积分终端滑模控制器(integral TSMC, ITSMC)具有与SFTSMC相似的特性,在消除奇异性的同时,保证系统有限时间稳定。传统滑模控制中符号函数的不连续切换特性所造成的控制不连续是引起抖振的根本原因。利用饱和函数代替符号函数来克服抖振的方法只能保证系统状态收敛到滑模面的邻域,降低滑模控制的鲁棒性和精度[12]。采用高阶滑模控制算法可以抑制抖振,但滑模面高阶导数信息要通过大量计算才能得到。文献[13]提出一种基于超螺旋算法(super-twisting algorithm,STA)的二阶滑模控制方法,不仅保持了高阶滑模控制能抑制抖振的优点,同时,无需对滑模面高阶求导。基于扩张状态观测器(extended state observer,ESO)的控制方法可以在保持控制性能的情况下消除模型不确定和外部扰动给系统带来的影响。文献[14]考虑模型不确定和外界干扰对FRR的影响,设计固定时间ESO (fixed-time ESO,FxTESO)与SFTSMC相结合的控制方法,实现对姿态角期望值的固定时间跟踪控制。文献[15]将滑模动态面控制技术和自适应滑模观测器技术结合,提出一种内外环自适应滑模动态面控制方法,使受到外部干扰的FRR能够对姿态角指令进行准确跟踪,但该方法仅仅保证闭环系统渐进稳定。文献[16]提出一种FRR自适应容错控制方法,设计基于FxTESO的SFTSMC,不仅能处理外部扰动和模型不确定对系统的影响,而且当执行机构发生故障时也能使系统保持稳定。本文提出一种基于FTESO和改进超螺旋算法(modified STA,MSTA)的积分终端滑模控制方法来解决FRR垂直回收无动力减速段姿态控制问题。采用FTESO对系统不可测量状态量和总扰动进行估计,进一步将状态量估计值引入积分终端滑模面,同时,基于总扰动估计值和MSTA设计改进超螺旋积分终端滑模控制器(modified super-twisting ITSMC,MSTITSMC),消除了传统终端滑模控制的奇异性,并有效抑制了抖振。本文首先在FRR绕质心运动方程基础上引入跟踪误差变量,建立姿态控制模型;然后,设计FTESO和MSTITSMC,进一步证明闭环系统有限时间稳定;最后,通过数值仿真验证所提出的控制方法的有效性和优越性。
1 数学模型及问题描述
1.1 绕质心运动方程
FRR的飞行剖面[17]如图1所示。本文考虑在无动力减速段的姿态控制问题。此阶段FRR在大气层内飞行且推力为0 N,其速度减小和姿态变化主要是受到气动力和气动力矩的作用。假设FRR是具有轴对称结构的刚体,体轴构成的坐标平面均为对称平面,其绕质心运动方程[14]为
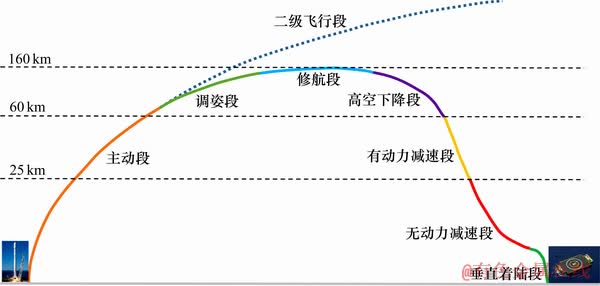
图1 FRR飞行剖面
Fig. 1 Flight profile of FRR
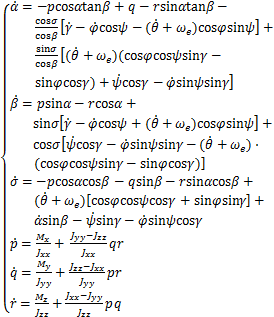 (1)
(1)
式中:α,β和σ分别为攻角、侧滑角和倾侧角;γ,ψ,φ和θ分别为航迹倾角、航迹偏角、经度、纬度;p,q和r分别为滚转、俯仰和偏航角速率;Mx,My和Mz分别为滚转、俯仰和偏航力矩;ωe=7.292 115×10-5 rad/s,为地球自转角速度;Jxx,Jyy和Jzz分别为沿x,y和z轴转动惯量。
1.2 面向控制的模型及问题描述
定义Ω=[α, β, σ]T, ,考虑模型不确定和外界干扰,则绕质心运动方程(1)可进一步描述为
,考虑模型不确定和外界干扰,则绕质心运动方程(1)可进一步描述为
 (2)
(2)
式中:Δf为表征模型不确定项变量;Δd为外部干扰;“ ”为叉乘运算;
”为叉乘运算;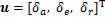 ,为控制输入;
,为控制输入;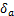 ,
,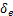 和
和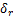 分别为控制滚转、俯仰和偏航的等效舵偏角;J为惯性矩阵,
分别为控制滚转、俯仰和偏航的等效舵偏角;J为惯性矩阵,
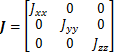
坐标转换矩阵R的具体表达式为
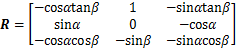
控制力矩矩阵B1 [14]的具体表达式为
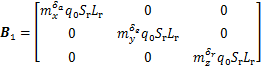
式中: ,
,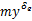 和
和 分别为滚转舵、俯仰舵和偏航舵的控制力矩系数;q0=0.5ρv2为动压;v为速度;
分别为滚转舵、俯仰舵和偏航舵的控制力矩系数;q0=0.5ρv2为动压;v为速度;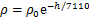 ,为大气密度;e为自然常数;h为飞行高度;ρ0=1.225 kg/m3,为海平面大气密度;
,为大气密度;e为自然常数;h为飞行高度;ρ0=1.225 kg/m3,为海平面大气密度; 和
和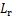 分别为FRR的参考面积和参考长度。
分别为FRR的参考面积和参考长度。
定义姿态角期望值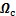 、姿态角跟踪误差
、姿态角跟踪误差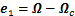 和角速率跟踪误差
和角速率跟踪误差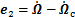 ,结合式(2)建立二阶姿态跟踪误差系统为
,结合式(2)建立二阶姿态跟踪误差系统为
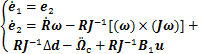 (3)
(3)
为了方便控制器设计,定义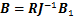 ,
,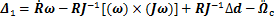 为总扰动,则式(3)简化为
为总扰动,则式(3)简化为
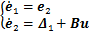 (4)
(4)
本文的主要目的是针对含有总扰动的二阶系统(4)设计控制器,使姿态跟踪误差 和
和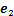 有限时间收敛。
有限时间收敛。
2 基于FTESO和MSTA的积分终端滑模控制方法
FRR姿态控制系统结构如图2所示,主要包括FTESO和MSTITSMC两部分。首先,基于姿态角跟踪误差 和控制输入
和控制输入 设计FTESO,得到角速率跟踪误差及总扰动的估计值
设计FTESO,得到角速率跟踪误差及总扰动的估计值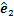 和
和 ;然后,基于观测器估计值和姿态角跟踪误差
;然后,基于观测器估计值和姿态角跟踪误差 设计MSTITSMC,实现对期望值的高精度快速跟踪。
设计MSTITSMC,实现对期望值的高精度快速跟踪。
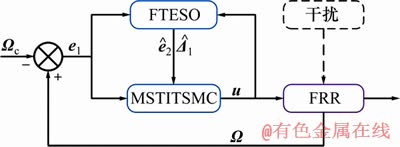
图2 FRR姿态控制系统结构
Fig. 2 Structure of FRR attitude tracking control system
2.1 定义与引理
定义1 对于向量 有如下定义:
有如下定义:
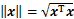
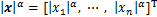
sig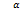 (x)
(x)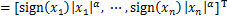
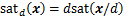
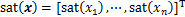
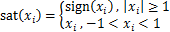
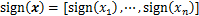
式中: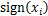 为符号函数。
为符号函数。
引理1[18]对于非线性系统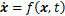 ,
,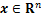 ,假设V(x)是定义在
,假设V(x)是定义在 的光滑正定函数。若存在正常数λ和
的光滑正定函数。若存在正常数λ和 使不等式
使不等式 ,
,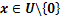 成立,则该系统是有限时间稳定的,收敛时间T满足
成立,则该系统是有限时间稳定的,收敛时间T满足
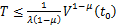 (5)
(5)
式中:V(t0)为V的初值。
引理2[19]考虑以下二阶系统:
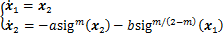 (6)
(6)
若02+ar+b为Hurwitz多项式的正常数,则上述系统是有限时间稳定的。
2.2 有限时间扩张状态观测器
假设1 总扰动Δ1及其导数有界,即 ,且满足
,且满足 。
。
在以上基础上,将式(4)增广为
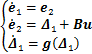 (7)
(7)
定义 ,
,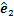 和
和 分别为e1,e2和Δ1的估计值,针对系统(7)设计FTESO为
分别为e1,e2和Δ1的估计值,针对系统(7)设计FTESO为
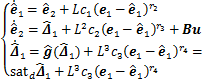 (8)
(8)
式中:r1=1;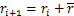 ;
; ,为任意偶数与奇数的比值;L>1;ci>0;
,为任意偶数与奇数的比值;L>1;ci>0; 。
。
定义FTESO观测误差分别为 ,
,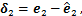
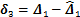 ,基于式(7)和式(8)建立的观测误差系统为
,基于式(7)和式(8)建立的观测误差系统为
 (9)
(9)
定义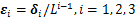 ,则式(9)可表示为
,则式(9)可表示为
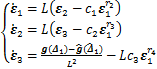 (10)
(10)
由文献[20]定理1可知,系统(10)的状态 ,
, 和
和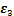 将在有限时间内收敛,即利用FTESO(8)可以在有限时间
将在有限时间内收敛,即利用FTESO(8)可以在有限时间 精确估计
精确估计 ,
,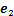 和
和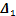 。
。
2.3 改进超螺旋积分终端滑模控制器
设计积分终端滑模面为
 (11)
(11)
式中: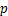 和
和 均为正奇数且
均为正奇数且 ;
;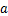 和
和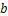 是使
是使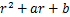 为Hurwitz多项式的正常数。
为Hurwitz多项式的正常数。
基于MSTA[21]设计趋近律为
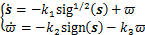 (12)
(12)
式中: ;
;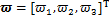 ;k1>0,k2>0, k3>0。
;k1>0,k2>0, k3>0。
结合式(11)和式(12),设计MSTITSMC为
 (13)
(13)
注1: 在传统SMC的滑模面中引入非线性积分项,构成积分终端滑模控制面,在保持传统SMC优点的同时,避免了控制器奇异性问题,且保证系统状态在滑动阶段有限时间收敛。
注2: 相较于标准STA[13]及其他MSTA[22],本文使用的MSTA通过在 的动态方程中增加1个关于
的动态方程中增加1个关于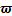 的线性项,即引入1个与自身状态相关的反馈,调节了高阶项的动态响应。根据MSTA设计的趋近律,不仅能抑制抖振,而且能保证系统状态有限时间收敛。
的线性项,即引入1个与自身状态相关的反馈,调节了高阶项的动态响应。根据MSTA设计的趋近律,不仅能抑制抖振,而且能保证系统状态有限时间收敛。
2.4 稳定性分析
定理 1对于二阶系统(4),采用所设计的FTESO(8)和MSTITSMC(13),能够使闭环系统有限时间稳定,即保证姿态跟踪误差 和
和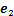 有限时间收敛。
有限时间收敛。
证明 定理1的证明可分3步。第1步证明在FTESO有限时间收敛过程中, 和
和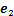 有限时间有界;第2步证明FTESO收敛后,
有限时间有界;第2步证明FTESO收敛后, 和
和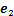 能在有限时间收敛至滑模面,
能在有限时间收敛至滑模面,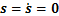 ;第3步证明收敛至滑模面后,
;第3步证明收敛至滑模面后, 和
和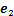 能沿滑模面有限时间收敛至平衡点。
能沿滑模面有限时间收敛至平衡点。
Step 1 对滑模面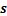 求导,得
求导,得
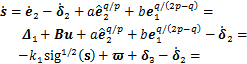
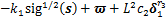 (14)
(14)
将式(13)代入式(4)可将闭环系统表示为
 (15)
(15)
选取Lyapunov函数:
 =
=
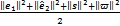 (16)
(16)
对V1求导,得
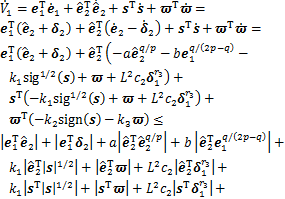
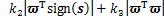 (17)
(17)
考虑不等式 ,
, ,
,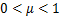 ,式(17)可表示为
,式(17)可表示为
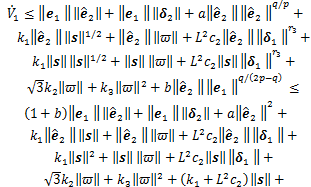
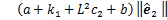 (18)
(18)
考虑不等式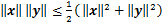 ,式(18)可表示为
,式(18)可表示为
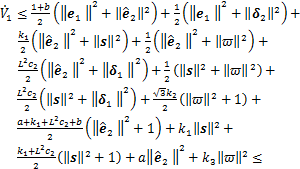
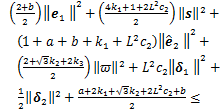
KV1+v (19)
式中:
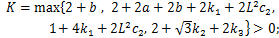
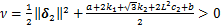 。
。
由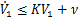 得
得
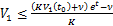 (20)
(20)
式中:V1(t0)为V1的初值。由于V1仅与时间t相关,显然V1在有限时间内有界,所以, 和
和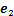 在有限时间内有界。
在有限时间内有界。
Step 2 当FTESO有限时间 收敛后,滑模面(11)可进一步表示为
收敛后,滑模面(11)可进一步表示为
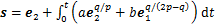 (21)
(21)
系统(15)可进一步表示为
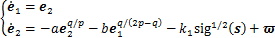 (22)
(22)
针对式(12),定义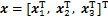 ,
, 。
。
对xi求导,得
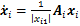 (23)
(23)
式中: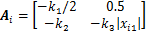 。
。
选取Lyapunov函数:
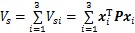 (24)
(24)
式中: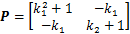 ,为正定的对称矩阵。
,为正定的对称矩阵。
对Vs求导,得
 (25)
(25)
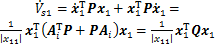 (26)
(26)
式中:
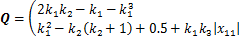
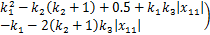
式(26)可进一步表示为
 (27)
(27)
式中:
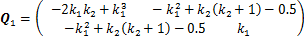
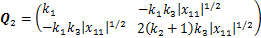
为了保证矩阵Q1和Q2正定,需要满足以下不等式:
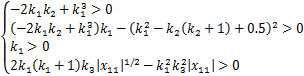 (28)
(28)
定义矩阵Q的最小特征值为λmin(Q),考虑不等式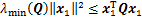 ,式(27)可表示为
,式(27)可表示为
 (29)
(29)
定义矩阵P最小特征值和最大的特征值分别为λmin(P)和λmax(P),考虑不等式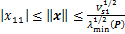 和
和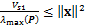 ,则式(29)可表示为
,则式(29)可表示为
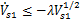 (30)
(30)
式中: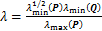
同理可证:若式(28)和不等式
 (31)
(31)
同时成立,则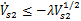 和
和 成立。
成立。
由此可知,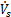 满足以下关系式:
满足以下关系式:
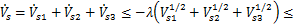
 (32)
(32)
由引理1可知,若参数k1,k2和k3同时满足式(28)和式(31),则当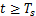 时,有
时,有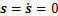 ,且
,且 满足
满足 ,其中
,其中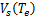 为
为 在
在 时的值。
时的值。
Step 3 当 和
和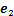 收敛至滑模面
收敛至滑模面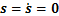 时,系统(22)可进一步表示为
时,系统(22)可进一步表示为
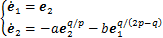 (33)
(33)
由引理2可知,上述系统在有限时间内稳定,即 和
和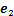 在有限时间内收敛。
在有限时间内收敛。
定理1证毕。
3 数值仿真与分析
为验证所设计FTESO+MSTITSMC方法的有效性,将其与文献[10]提出的SFTSMC方法、文献[14]提出的FxTESO+SFTSMC方法在MATLAB/ Simulink中的数值仿真结果进行对比。
仿真中,FRR的相关参数来源于文献[14];初始姿态角为Ω0=[-17, -0.573, -1.146]T (°);初始角速率为ω0=[-8.239 7×10-4, -0.005 3, -1.596 9×10-4]T (°)/s;绕质心运动方程中含有描述质心运动的6个时变状态量,可通过对质心运动方程数值积分得到。为完成仿真,设置状态量的初值为φ0=-47°,ψ0=0°,γ0=-41°,θ0=-47.15°,v0=1 180 m/s,h0= 25 000 m;姿态角期望值Ωc=[5t/30-5, 2t/30-1, 0]T(°);气动系数偏差、转动惯量偏差和大气密度偏差为+20%,质量偏差为100 kg;所受扰动力矩为Δd=104[1+sin(πt/2+π/6), 1+sin(πt/2+π/3)]T N·m;等效舵偏角限制在[-30°, 30°];仿真步长为5 ms,仿真时长为30 s。
本文设计的方法FTESO参数设置为L=5, d=4,c1=c2=10,c3=12, ;MSTITSMC参数设置为a=15,b=50,p=13,q=11,k1=0.70, k2=0.10,k3=0.01。对比的2种方法参数设置与文献[10]和[14]中的一致。
;MSTITSMC参数设置为a=15,b=50,p=13,q=11,k1=0.70, k2=0.10,k3=0.01。对比的2种方法参数设置与文献[10]和[14]中的一致。
图3~5所示为FRR姿态角跟踪曲线。从图3~5可见:与FxTESO+SFTSMC方法相比,本文设计的方法能在更短时间对姿态角期望值实现稳定跟踪,在动态响应过程中的超调量也更小,而无观测器的SFTSMC方法姿态角跟踪误差较大,在跟踪倾侧角期望值时发生了明显偏离。
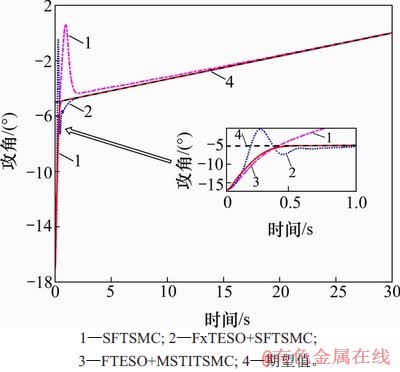
图3 攻角跟踪曲线
Fig. 3 Tracking curves of attack angle
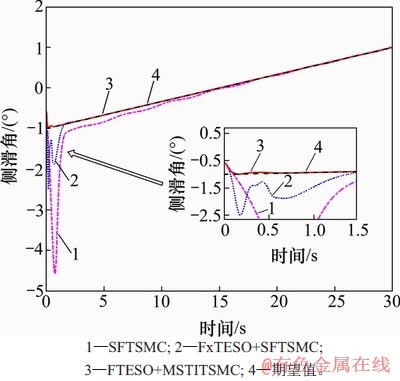
图4 侧滑角跟踪曲线
Fig. 4 Tracking curves of sideslip angle
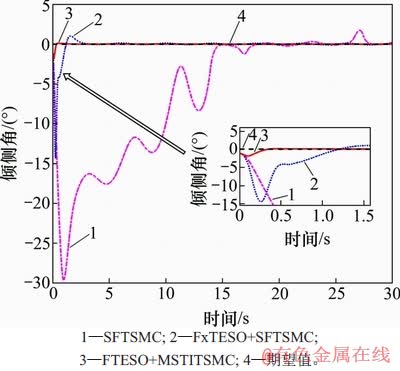
图5 倾侧角跟踪曲线
Fig. 5 Tracking curves of bank angle
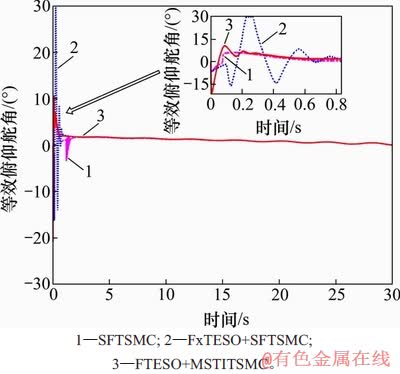
图6 等效俯仰舵角曲线
Fig. 6 Curves of equivalent pitch rudder angle
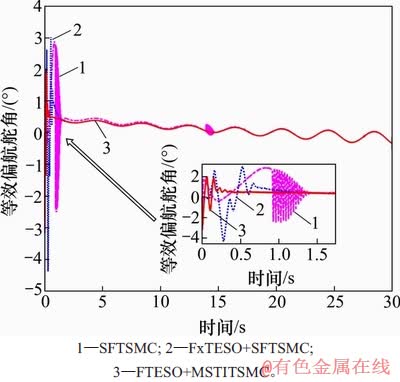
图7 等效偏航舵角曲线
Fig. 7 Curves of equivalent yaw rudder angle
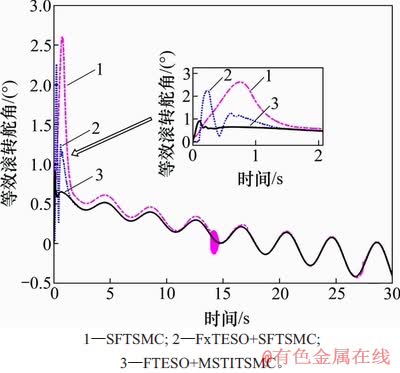
图8 等效滚转舵角曲线
Fig. 8 Curves of equivalent roll rudder angle
图6~8所示为等效舵偏响应曲线。从图6~8可见:FxTESO+SFTSMC方法的等效俯仰舵偏δe在0.2~0.3 s到约束上界,其余2种方法输出的舵偏响应均在合理幅值范围内。
图9所示为滑模面的变化曲线。从图9可以看出本文设计的方法对应的滑模面s1,s2和s3分别在1.0,0.5和1.5 s左右收敛,且收敛过程较平滑,无明显抖振。综上所述,本文设计的FTESO+MSTITSMC方法能准确、快速地跟踪姿态角期望值,且对扰动有较好抑制效果。
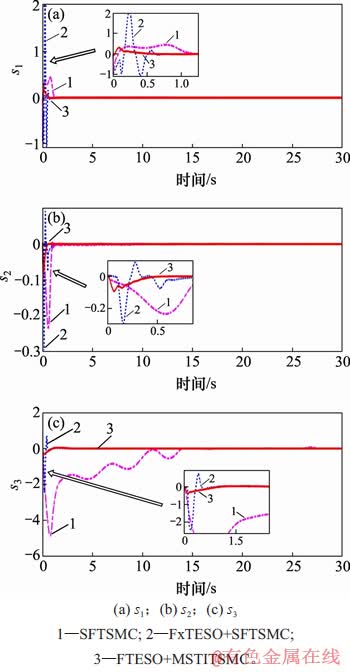
图9 滑模面曲线
Fig. 9 Curves of sliding mode variable
4 结论
1) 针对FRR垂直回收过程无动力减速段存在模型不确定和外部扰动等情况,提出一种基于FTESO和MSTA的积分终端滑控制方法。采用FTESO对姿态角速度和总扰动进行估计,将角速度估计值引入积分终端滑模面,同时,基于总扰动估计值和MSTA设计了MSTITSMC。
2) 基于Lyapunov理论证明了闭环系统有限时间稳定;将本文设计的方法与2种非奇异快速终端滑模控制方法进行仿真对比,发现本文设计的方法对模型不确定和外部扰动具有较强鲁棒性,能对姿态角期望值进行准确和快速跟踪。
参考文献:
[1] 王振国, 罗世彬, 吴建军, 等. 可重复使用运载器研究进展[M]. 长沙: 国防科技大学出版社, 2004: 1-2.
WANG Zhenguo, LUO Shibin, WU Jianjun, et al. Recent progress on reusable launch vehicle[M]. Changsha: National University of Defense Technology Press, 2004: 1-2.
[2] 徐大富, 张哲, 吴克, 等. 垂直起降重复使用运载火箭发展趋势与关键技术研究进展[J]. 科学通报, 2016, 61(32): 3453-3463.
XU Dafu, ZHANG Zhe, WU Ke, et al. Recent progress on development trend and key technologies of vertical take-off vertical landing reusable launch vehicle[J]. Chinese Science Bulletin, 2016, 61(32): 3453-3463.
[3] SUN Jingguang, SONG Shemin, WU Guanqun. Tracking control via robust dynamic surface control for hypersonic vehicles with input saturation and mismatched uncertainties[J]. International Journal of Innovative Computing, 2017, 13(6): 2067-2087.
[4] TANG Tingting, QI Ruiyun, JIANG Bin. Adaptive nonlinear generalized predictive control for hypersonic vehicle with unknown parameters and control constraints[C]//Proceedings of the Institution of Mechanical Engineers, Part G: Journal of Aerospace Engineering, 2019, 233(2): 510-532.
[5] WANG Zhen, WU Zhong, DU Yijiang. Robust adaptive backstepping control for reentry reusable launch vehicles[J]. Acta Astronautica, 2016, 126(s1): 258-264.
[6] BHAT S P, BERNSTEIN D S. Continuous finite-time stabilization of the translational and rotational double integrators[J]. IEEE Transactions on Automatic Control, 1998, 43(5): 678-682.
[7] 韩钊, 宗群, 田柏苓, 等. 基于Terminal滑模的高超声速飞行器姿态控制[J]. 控制与决策, 2013, 28(2): 259-263, 268.
HAN Zhao, ZONG Qun, TIAN Bailing, et al. Hypersonic vehicle attitude control using Terminal sliding mode control[J]. Control and Decision, 2013, 28(2): 259-263, 268.
[8] YU Xinghuo, MAN Zhihong. Fast terminal sliding-mode control design for nonlinear dynamical systems[J]. IEEE Transactions on Circuits and Systems I: Fundamental Theory and Applications, 2002, 49(2): 261-264.
[9] MAN Zhihong, YU X H. Terminal sliding mode control of MIMO linear systems[J]. IEEE Transactions on Circuits and Systems I: Fundamental Theory and Applications, 1997, 44(11): 1065-1070.
[10] LI Huijie, CAI Yuanli. On SFTSM control with fixed-time convergence[J]. IET Control Theory & Applications, 2017, 11(6): 766-773.
[11] LI Peng, MA Jianjun, GENG Lina, et al. Integral terminal sliding mode control for uncertain nonlinear systems[C]//2015 34th Chinese Control Conference(CCC). Hangzhou, China, IEEE, 2015: 824-828.
[12] 杨洁. 高阶滑模控制理论及其在欠驱动系统中的应用研究[D]. 北京: 北京理工大学自动化学院, 2015:18-19.
YANG Jie. Higher-order sliding mode control theory and its application on underactuated systems[D]. Beijing: Beijing Institute of Technology. School of Automation, 2015: 18-19.
[13] SHTESSEL Y B, SHKOLNIKOV I A, LEVANT A. Smooth second-order sliding modes: Missile guidance application[J]. Automatica, 2007, 43(8): 1470-1476.
[14] ZHANG Liang, WEI Changzhu, WU Rong, et al. Fixed-time extended state observer based non-singular fast terminal sliding mode control for a VTVL reusable launch vehicle[J]. Aerospace Science and Technology, 2018, 82/83: 70-79.
[15] 钱默抒, 熊克, 王海洋. 重复使用运载火箭精确回收滑模动态面控制[J]. 宇航学报, 2018, 39(8): 879-888.
QIAN Moshu, XIONG Ke, WANG Haiyang. Sliding mode dynamic surface control in precise recovery phase for reusable launch vehicle[J]. Journal of Astronautics, 2018, 39(8): 879-888.
[16] ZHANG Liang, WEI Changzhu, WU Rong, et al. Adaptive fault-tolerant control for a VTVL reusable launch vehicle[J]. Acta Astronautica, 2019, 159: 362-370.
[17] 韦常柱, 琚啸哲, 徐大富, 等. 垂直起降重复使用运载器返回制导与控制[J]. 航空学报, 2019, 40(7): 197-220.
WEI Changzhu, JU Xiaozhe, XU Dafu, et al. Guidance and control for return process of vertical takeoff vertical landing reusable launching vehicle[J]. Acta Aeronautica et Astronautica Sinica, 2019, 40(7): 197-220.
[18] 王世峰, 赵党军. 基于有限时间收敛ESO的四旋翼无人机控制[J]. 中南大学学报(自然科学版), 2015, 46(7): 2494-2503.
WANG Shifeng, ZHAO Dangjun. Quad-rotor vehicle control based on finite-time convergent ESO[J]. Journal of Central South University(Science and Technology), 2015, 46(7): 2494-2503.
[19] BHAT S P, BERNSTEIN D S. Geometric homogeneity with applications to finite-time stability[J]. Mathematics of Control, Signals, and Systems, 2005, 17(2): 101-127.
[20] LAN Qixun, QIAN Chunjiang, LI Shihua. Finite-time disturbance observer design and attitude tracking control of a rigid spacecraft[J]. Journal of Dynamic Systems, Measurement, and Control, 2017, 139(6): 061010-1-061010-8.
[21] YANG Yi, QIN Shiyin, JIANG Ping. A modified super-twisting sliding mode control with inner feedback and adaptive gain schedule[J]. International Journal of Adaptive Control and Signal Processing, 2017, 31(3): 398-416.
[22] 宗群, 张睿隆, 董琦, 等. 固定翼无人机自适应滑模控制[J]. 哈尔滨工业大学学报, 2018, 50(9): 147-155.
ZONG Qun, ZHANG Ruilong, DONG Qi, et al. Adaptive sliding mode control for fixed-wing unmanned aerial vehicle[J]. Journal of Harbin Institute of Technology, 2018, 50(9): 147-155.
(编辑 陈灿华)
收稿日期: 2019 -08 -04; 修回日期: 2019 -11 -22
基金项目(Foundation item):国家自然科学基金资助项目(11272349);航天器设计优化与动态模拟技术教育部重点实验室(北京航空航天大学)开放基金资助项目(2019KF006)(Project(11272349) supported by the National Natural Science Foundation of China; Project(2019KF006) supported by the Key Laboratory of Spacecraft Design Optimization and Dynamic Simulation Technologies(Beihang University) of Ministry of Education)
通信作者:廖宇新,博士,讲师,从事高超声速飞行器轨迹优化、制导与控制研究;E-mail:liaoyuxin@csu.edu.cn