DOI: 10.11817/j.issn.1672-7207.2015.03.015

基于改进的本征时间尺度分解和基本尺度熵的齿轮故障诊断方法

钟先友^{1, 2}，赵春华¹，陈保家¹，曾良才²

(1. 三峡大学 水电机械设备设计与维护湖北省重点实验室，湖北 宜昌，443002；

2. 武汉科技大学 冶金装备及其控制教育部重点实验室，湖北 武汉，430081)

摘要：针对齿轮振动信号的非线性、非平稳特征和难以获取大量故障样本的问题，提出改进的本征时间尺度分解方法(IITD)和基本尺度熵(BE)的齿轮故障诊断方法。采用IITD方法对齿轮振动信号进行分解，再对得到的前4个有意义的合理旋转(PR)分量计算其基本尺度熵，并将熵值作为特征向量输入支持向量机分类器，从而实现齿轮故障类别的诊断。实验结果表明，该方法能有效地实现齿轮故障类型的诊断。

关键词：本征时间尺度分解；基本尺度熵；支持向量机；样本熵

中图分类号：TH113.1；TN911.7              文献标志码：A         文章编号：1672-7207(2015)03-0870-08

Gear fault diagnosis method based on IITD and base-scale entropy

ZHONG Xianyou^{1, 2}, ZHAO Chunhua¹, CHEN Baojia¹, ZENG Liangcai²

(1. Hubei Key Laboratory of Hydroelectric Machinery Design & Maintenance, China Three Gorges University,

Yichang 443002, China;

2. Key Laboratory of Metallurgical Equipment and Control of Education of Ministry,

Wuhan University of Science and Technology, Wuhan 430081, China)

Abstract: Considering the nonlinear, non-stationary characteristics of a gear vibration signal，and difficulty in obtaining a large number of failures samples, a gear fault diagnosis method combining improved intrinsic time-scale decomposition (IITD) and base-scale entropy was proposed. Firstly, IITD method was applied to decompose the vibration signal into a finite number of proper rotation (PR) components, then the first four proper rotation components were selected to calculate entropy, and finally the entropy values as feature vectors were input to a SVM-based classifier to distinguish the gear fault types. The results show that the proposed method can diagnose the fault categories effectively.

Key words: intrinsic time-scale decomposition; base-scale entropy; support vector machine; sample entropy

齿轮是动力传递的重要组成部分，它的健康状况将直接影响到整机的正常运行，其状态监测和故障诊断一直受重视。齿轮发生故障时，其振动信号通常表现出非线性、非平稳特征。在目前的非平稳信号处理方法中，常用于齿轮故障诊断的方法有小波变换^[1-4]、经验模式分解(EMD)^[5-8]和局部均值分解(LMD)^[9-11]。但是这些方法都存在着一定的局限性。Frei等^[12]提出了一种自适应时频分析方法 —— 本征时间尺度分解方法(ITD)，并将这种方法应用于生物医学信号处理中，取得了较好的效果。ITD方法能够自适应地将一个复杂信号分解为若干个瞬时频率具有物理意义的PR分量之和。与EMD相比，ITD在计算效率方面有明显优势，适合在线分解。林近山把^[13]ITD算法成功的应用于齿轮箱的故障诊断中，但ITD算法中对基线的定义是基于信号本身的线性变换，因此从第二个分量开始，有明显的信号失真。杨宇等^[14]采用三次样条插值对ITD方法进行改进并应用到转子的故障诊断中。但3次样条拟合基线时会产生的过包络、欠包络问题，针对这个问题，本文作者提出新的拟合基线的方法改进ITD方法。Richman等^[15]提出的样本熵，是近似熵的改进算法，与近似熵相比，它可以较少地依赖于时间序列长度，已经应用于机械故障诊断中^[16-17]，但计算量大。李锦等^[18]提出基本尺度熵方法并成功地应用于心率变异性分析上。基本尺度熵简单、抗干扰能力强且运算快速，适合于非平稳信号分析。本文尝试把基本尺度熵引入到齿轮信号分析上。齿轮的不同运行状态表征着不同的内在模式复杂性，不确定性越大，复杂性越大，熵也越大，特别是对某些具体故障而言，由于故障信息往往集中在某一敏感频带中，当故障发生时，该敏感频带内的振动信号会发生较大的变化，即该频段的复杂性也发生了变化，因此，可以用基本尺度熵表征齿轮振动信号的复杂性的变化。研究发现：对齿轮的4种状态下的原始振动信号求基本尺度熵，其基本尺度熵值比较接近，区分效果不明显。故本文作者对齿轮的振动信号进行自适应的IITD分解，分解的各个PR分量包含了原始振动信号不同频段的特征信息，再对各分量计算基本尺度熵，减少了信号间特征信息的干涉或耦合，增强了区分效果，更好地实现了故障特征的分离。支持向量机作为一种较新的模式识别方法，与神经网络模型相比，在小样本下具有结构简单、泛化能力强、学习速率快等优点，在模式分类、数据预测等领域有广泛的应用。基于此，本文作者结合支持向量机，提出基于IITD和基本尺度熵的齿轮故障诊断方法，实验结果表明本文提出的方法能够有效区分齿轮的故障类型。

1  ITD方法

ITD方法能够自适应地将一个复杂信号分解为若干个相互独立的合理旋转分量和一个趋势项之和。设X_t是待分析的原信号，分解前先定义一个基线提取算子Ｌ，使得从原始信号中去掉该基线后剩下的余量信号成为一个合理旋转分量。一次分解的表达式为^[12]：

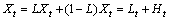         (1)

1) 确定信号X_t的极值点X_k及对应的时刻τ_k(k=1, 2, …, M，M为所有极值点的个数)，并计算

k=1, 2, …, M -2              (2)

式中：0＜a＜1，一般地，a=0.5。

2) 定义信号的分段线性基线提取算子如下：

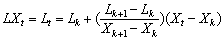
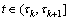                (3)

3) 将基线信号L_t作为原始信号，重复上述步骤，直到基线信号为一单调函数或常函数。原始信号被分解为

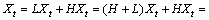
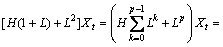
            (4)

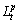其中：为第i次迭代分离出的合理旋转分量，为单调函数或常函数。

考察式(5)所示信号

x(t) = x₁(t) + x₂(t) + x₃(t)= 20cos(80πt+sin(40πt))+10cos(30πt)+2cos(10πt) t ∈ [0,1]                 (5)

式中：x₁(t)为调频信号，x₂(t)和x₃(t)为2个余弦信号，时域波形如图1所示。对x(t)进行ITD分解，得到的分解结果如图2所示，其中P_R1，P_R2和P_R3分别为ITD分解的前3个分量，R为残余分量。

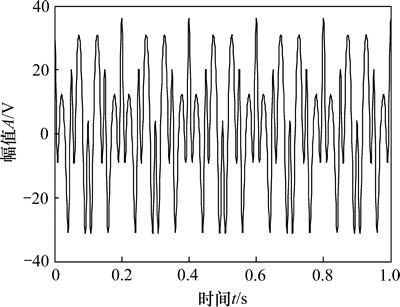
图1  仿真信号的时域波形

Fig. 1  Time domain of simulated signal

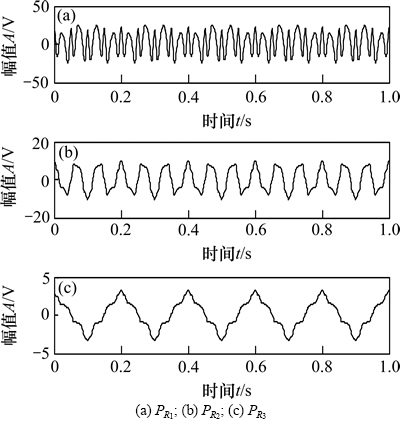
图2  仿真信号的ITD分解结果

Fig. 2  ITD decomposition results of simulation signal

从图2可以看出：P_R1分量、P_R2分量和P_R3分量分别对应于仿真信号x(t)的3个分量x₁(t)，x₂(t)和x₃(t)，第2个分量和第3个分量出现了失真，这是由于ITD方法中是以原始信号任意2个相邻的极值点为跨度对信号进行分段线性变换来构造基线信号，这导致第2个分量和第3个分量信号波形出现了毛刺而失真。因此，本文对ITD方法进行改进，用新的拟合基线的方法来代替ITD方法中的线性变换方法。

2  基线拟和方法比较

图3所示为各种插值方法比较。曲线拟和的常用方法有线性插值、三次多项式插值和三次样条插值，用上述3种方法分别用对离散点进行插值，由图3(a)~(c)可看出：三次样条插值法虽具有比较理想的光滑性，具有二阶连续可微性，但会引起“过冲”现象(图3(c)中的点B处)。三次多项式插值光滑性不如三次样条。如果既能保证络有足够的光滑性，又能避免“过冲”现象，对基线的拟合很有意义。为此，提出结合三次样条插值和三次多项式插值的混合方法，设y₁为三次样条拟合的结果，y₂为三次多项式插值拟合的结果，用0.3y₁+0.7y₂作为最终的拟合结果，则拟合出的曲线既能有效避免“过冲”现象，又保持了三次样条插值法的优点。其拟合的结果如图3(d)所示，从图3(d)中可以看出：拟合效果较好，避免“过冲”现象，且具有比较理想的光滑性。

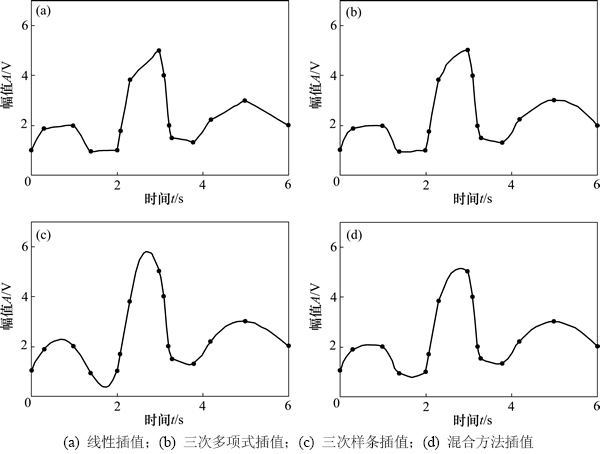
图3  各种插值方法比较

Fig. 3  Comparison of various interpolation methods

3  IITD方法

IITD方法基本的分解过程如下：

1) 确定原始信号X_t所有的局部极值点，方法与ITD相同，通过式(2)和(3)和计算各基线的控制点X_k。

2) 对序列端点采用镜像对称延拓方法进行延拓，得到左右两端点极值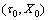和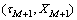，令k分别等于0和M，按式(2)求出L₁与L_M的值，然后对所有L_k用图3(c)中所用的方法来拟合，得到基线信号L₁。

3) 将L₁从原始信号中分离出来，得到P₁，若P₁是一个P_R分量，则P₁作为信号X_t的第1个分量，否则将P₁作为原始信号重复上述步骤，循环k次，直到得到P_k是一个PR分量，P_k即为信号X_t的第1个P_R分量P_R1，将P_R1信号中分离出来，得到一个新的信号r₁。

4) 再将r₁作为原始信号重复上面的步骤，得到X_t的第2个满足条件的P_R2。重复循环n次，得到信号X_t的n个满足P_R条件的分量，直到r_n为一单调函数或常函数，这样就把X_t分解为n个P_R分量和一个单调或常函数之和，即：

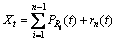           (6)

用IITD方法对图1中的仿真信号x(t)进行分解，得到的分解结果如图4所示。从图4中可以看出：IITD方法对第2个分量和第3个分量的分解也取得较好的效果。对于图1所示的信号，分别用EMD，ITD和IITD进行分解，比较三者的分解效果，在同一台电脑上，各运行20次，取平均值，t表示3种方法分解的时间，用r₁和r₂表示分解得到的第1个分量和第2个分量与真实信号的相关系数。结果如表1所示。

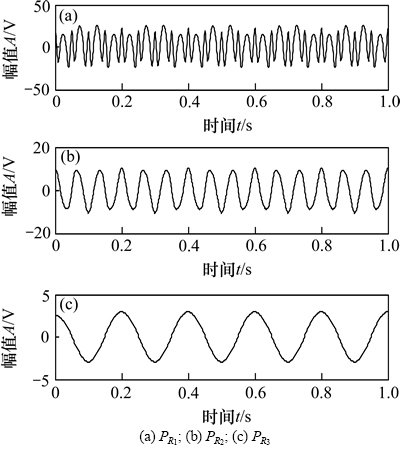
图4  仿真信号的IITD分解结果

Fig. 4  IITD decomposition results of simulation signal

表1  3种方法分解效果比较

Table 1  Comparison of three methods of decomposition

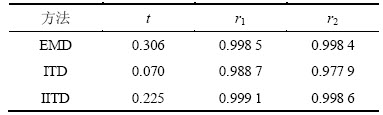
从表1可以看出：ITD分解速度最快，但分解所得的分量与真实分量的相关性最小，而IITD分解速度比EMD快，且分解所得的分量与真实分量的相关性最大，与另外2种分解方法相比具有一定的优势。

为了进一步比较ITD与IITD的分解效果，考察式(7)所示信号：

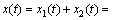
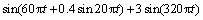
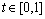                (7)

式中：x₁(t)为调频信号，x₂(t)为正弦信号，分别用ITD和IITD方法对仿真信号x(t)进行分解，求时频谱，结果如图5和图6所示，从图5可以看出：由于ITD的分解误差，30 Hz正弦瞬时频率出现了明显的局部变形，导致ITD的时频谱频率分辨率低，而在图6中，30 Hz正弦瞬时频率局部变形较小，且能看出调频特征，IITD的时频谱频率分辨率明显提高，体现出IITD的优势。

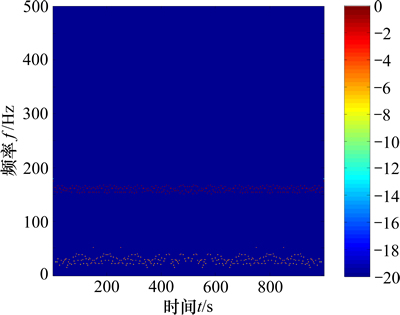
图5  信号的ITD时频图

Fig. 5  Time-frequency distribution based on ITD of signal

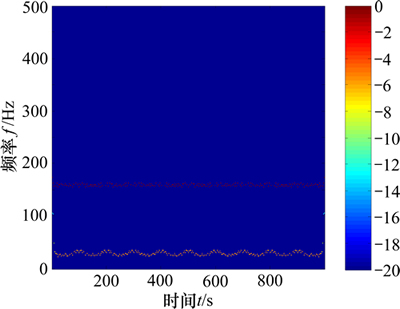
图6  信号的IITD时频图

Fig. 6  Time-frequency distribution based on ITD of signal

4  基本尺度熵的基本原理

基本尺度熵的详细计算方法参见文献[18]，简要步骤如下。

对于数据长度为N的时间序列u：，对于每一个u(i)，取m个连续点组成一m维矢量：

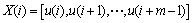       (8)

共有N-m+1个m维矢量。对于每一个m维矢量，计算出基本尺度B_S，B_S定义为m维矢量中所有相邻点数据间隔(或大小)的差值平均根值，即：

       (9)

根据基本尺度，选取了划分符号的标准为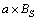，然后把每一个m维矢量转换成m维矢量符号序列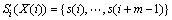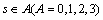，。具体的转换如下：

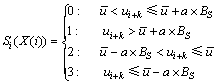
i=1, 2, …, N-m+1，k=0, 1, …, m-1。为第i个m维矢量的平均值，B_S为第i个m维矢量的基本尺度。符号0，1，2，3只是作为每一个划分区域的标记，具体的大小没有实际意义，目的是为了便于统计概率的方便。a为一个特殊参数，a取值过大，会导致细节信息的丢失，不能很好地捕捉到信号中的动态信息，a取值过小会导致噪声的明显的影响。

统计m维矢量符号序列S_i的分布概率P(S_i)。包含0，1，2，3共4种符号的m维矢量符号序列S_i共有4^m种不同的组合状态π。每一种组合状态都代表着m维矢量的一种波动模式，统计每一种不同的组合状态在整个N-m+1个m维矢量中所占的概率：

      (11)

其中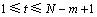：，#表示个数。

基本尺度熵定义为

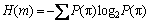         (12)

其中：m的取值可以从3到7，N的取值只要大于4^m即可。公式中对所有可能状态π的分布概率求信息熵H(m)，该信息熵描述了时间序列中m个连续值所包含的波动信息。很显然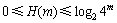，，如果时间序列只出现1种可能状态，那么H(m)=0；如果时间序列出现π种概率分布相同的状态，那么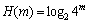；如果时间序列出现若干种可能状态，则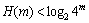。熵值越大，表明序列m维矢量的波动模式越复杂，序列的复杂性越高，反之，熵值越小，序列的复杂性越低。

5  基于IITD、基本尺度熵和SVM的故障诊断方法

基于IITD、基本尺度熵和支持向量机^[19-20]的齿轮故障诊断方法的步骤如下：首先采用方法将齿轮的振动加速度信号自适应地分解为若于个P_R分量，每个P_R分量都包含了原信号不同频段的故障信息，因此，通过对每个分量进行特征提取，就可以得到原始信号的故障特征，由于故障信息一般集中在高频段，因此，选取前4个有意义的分量并计算每个分量的基本尺度熵，并将其作为特征向量输入支持向量机实现故障类型的分类。基于IITD、基本尺度熵和支持向量机的齿轮故障诊断方法的流程如图7所示。

6  实验数据分析

为了检证本文所提方法在齿轮故障诊断中的有效性，对齿轮振动信号进行分析。齿轮状态包括正常、轻度磨损、中度磨损和断齿故障，实验装置介绍详见文献[21], 采样频率为16 384 Hz，采样长度为2 048。对4种故障状态的原始振动信号每种状态取5组数据求取基本尺度熵及其均值如表2所示。

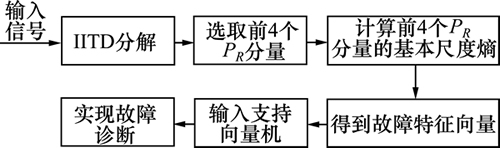
图7  基于IITD、基本尺度熵和SVM的齿轮故障诊断方法流程图

Fig. 7  Flow chart of gear fault diagnosis based on IITD, base-scale entropy and SVM

表2  各种状态下齿轮信号的基本尺度熵

Table 2  Base-scale entropy of gear signals under different conditions

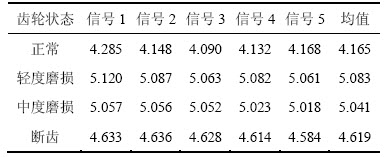
从表2可以看出：原始信号的基本尺度熵值可以区分4种状态，但轻度磨损和中度磨损2种故障状态的基本尺度熵比较接近，区分效果不明显。正常状态下齿轮箱的基本尺度熵比较小，这是因为齿轮箱处于正常状态时，齿轮箱振动信号比较规则和简单；当齿轮箱的故障状态变为轻度磨损时，齿轮箱的振动信号产生新模式的概率开始增大，因而时间序列逐渐变得更加复杂, 其基本尺度熵逐渐变大；当齿轮箱的故障状态变为中度磨损时，随着齿轮箱故障程度的加剧，齿轮箱振动信号中的规则分量又开始增加，因而时间序列逐渐变得更加简单和规则，其基本尺度熵逐渐变小；当齿轮箱的故障状态由中度磨损变为断齿时，齿轮箱振动信号中的规则分量继续增加, 因而时间序列逐渐变得更加简单和规则, 其基本尺度熵进一步变小。基本尺度熵准确地反映了齿轮箱故障状态的变化过程，因此，可以用基本尺度熵表征齿轮振动信号的复杂性的变化。

由于原始齿轮振动信号的基本尺度熵的区分效果不明显，所以尝试对每组原始振动信号进行IITD分解后求每个分量的基本尺度熵来进行区分。对每种齿轮箱故障状态分别采集30组数据, 用各组中任意的15组数据作为样本，然后用剩下的每15组数据作为测试数据。对样本数据，首先采用IITD分解，得到一系列P_R分量，由于齿轮振动信号的主要信息在高频段，因此选取前4个P_R分量求基本尺度熵，以此作为故障特征向量输入到SVM中进行训练，表3所示为训练集数据(限于篇幅，仅列出每种状态各4组数据)。

表3  齿轮各种状态下的特征向量

Table 3  Eigenvector of gear under different conditions

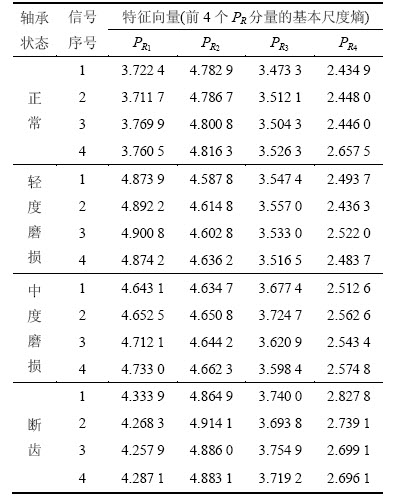
齿轮信号IITD分解的第一个P_R分量幅值最大，包含信号的主要信息，从表3的第3列来比较第一分量的基本尺度熵值，可以看出各状态下的振动信号的第一分量的基本尺度熵有了明显的差异，其他分量的基本尺度熵值的取值范围也不同，故可以通过分类器进行准确故障分类。

PSO是一种新的群体智能优化算法，与遗传算法类似，但没有遗传算法的交叉和变异，群体中的各个粒子在迭代中通过追随最优粒子在解空间中搜索最优解，具有更快的收敛速度。SVM参数选择对分类精度影响较大，而SVM参数选择没有确定的准则。本文在训练SVM时使用粒子群优化算法确定最优参数。

利用粒子群对支持向量机的参数进行优化，最大迭代数为200步，寻优结果确定最优参数c=1.29，g=117.55，利用最优参数c和g进行支持向量机故障识别，将每种状态振动信号中剩余的15组同样计算出特征向量，输入已经训练好的支持向量机中进行故障的模式识别，其结果见表4。从表4可见：本文所提的方法能够对测试样本进行正确率很高的故障诊断，表明基于IITD、基本尺度熵值和支持向量机的齿轮故障诊断方法是有效的。

为了与样本熵进行对比，对同样的数据，在故障4种状态下分别取30组数据，用各组中任意的15组数据作为样本，然后用剩下的每15组数据作为测试数据。对样本数据，首先采用IITD分解，得到一系列P_R分量，取前4个P_R分量求样本熵，以此作为故障特征向量输入到SVM中进行训练，利用粒子群对支持向量机的参数进行优化，其诊断结果如表4所示。

表4  齿轮故障诊断结果

Table 4  Fault diagnosis results of gear

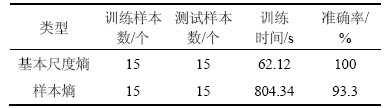
从表4可以看出：基本尺度熵识别齿轮的准确率比样本熵高; 样本熵也取得了较高的准确率，但与基本尺度熵相比，训练时间明显大于基本尺度熵，结果表明，本文所提的方法更具优势。

7  结论

1) 所提出的IITD方法是一种自适应时频分析方法，可以解决ITD方法分解信号产生的波形失真问题。

2) 基于IITD和基本尺度熵的齿轮故障诊断方法能有效地实现齿轮故障类型的诊断，准确率高。

3) 对比较样本熵的识别效果，结果表明基本尺度熵在耗时和准确率方面更具优势。

参考文献：

[1] Wang W J, McFadden P D. Application of wavelets to gear box vibration signals for fault detection[J]. Journal of Sound and Vibration, 1996, 192(5): 927-937.

[2] 张进, 冯志鹏, 褚福磊. 基于时间-小波能量谱的齿轮故障诊断[J]. 振动与冲击, 2011, 30(1): 157-161.

ZHANG Jin, FENG Zhipeng, CHU Fulei. Fault diagnosis of gear based on time-wavelet energy spectrum[J]. Journal of Vibration and Shock, 2011, 30(1): 157-161.

[3] LI Hui, ZHANG Yuping, ZHENG Haiqi. Application of Hermitian wavelet to crack fault detection in gearbox[J]. Mechanical Systems and Signal Processing, 2011, 25(4): 1353-1363.

[4] 何岭松, 李巍华. 用Morlet小波进行包络检波分析[J].振动工程学报, 2002, 15(1): 119-121.

HE Lingsong, LI Weihua. Morlet wavelet and its application in enveloping[J]. Journal of Vibration Engineering, 2002, 15(1): 119-121.

[5] 程军圣, 于德介, 杨宇. 基于EMD的能量算子解调方法及其在机械故障诊断中的应用[J]. 机械工程学报, 2004, 40(8): 115-118.

CHENG Junsheng, YU Dejie, YANG Yu. Energy operator demodulating approach based on EMD and its application in mechanical fault diagnosis[J]. Chinese Journal of Mechanical Engineering, 2004, 40(8): 115-118.

[6] CHENG Junsheng, YU Dejie, YANG Yu. Energy operator demodulating approach based on EMD and its application in mechanical fault diagnosis[J]. Chinese Journal o f Mechanical Engineering, 2004, 40(8): 115-118 .

[7] Liu B, Riemenschneider S, Xu Y. Gearbox fault diagnosis using empirical mode decomposition and Hilbert spectrum[J]. Mechanical Systems and Signal Processing, 2006, 20(3): 718-734.

[8] LI Hui, ZHANG Yuping, ZHENG Haiqi. Wear detection in gear system using Hilbert-Huang transform[J]. Journal of Mechanical Science and Technology, 2006, 20(11): 1781-1789.

[9] 张亢, 程军圣, 杨宇. 基于局部均值分解的阶次跟踪分析及其在齿轮故障诊断中的应用[J]. 中国机械工程, 2011, 22(14): 1732-1736.

ZHANG Kang, CHENG Junsheng, YANG Yu. The local mean decomposition method and its application to gear fault diagnosis[J]. China Mechanical Engineering, 2011, 22(14): 1732-1736.

[10] 陈保家, 何正嘉, 陈雪峰, 等. 机车故障诊断的局域均值分解解调方法[J]. 西安交通大学学报, 2010, 44(5): 40-44.

CHEN Baojia, HE Zhengjia, CHEN Xuefeng, et al. Locomotive fault diagnosis based on local mean decomposition demodulating approach[J]. Journal of Xi’an Jiao Tong University, 2010, 44(5): 40-44.

[11] 钟先友, 曾良才, 赵春华. 局域均值分解和1.5维谱在机械故障诊断中的应用[J]. 中国机械工程, 2013, 24(4): 452-457.

ZHONG Xianyou, ZENG Liangcai, ZHAO Chunhua. Application of local mean decomposition and 1.5 dimension spectrum in machinery fault diagnosis[J]. China Mechanical Engineering, 2013, 24(4): 452-457.

[12] Frei M G, Osorio I. Intrinsic time-scale decomposition: Analysis and real-time filtering of non-stationary signals[J]. Proceedings of the Royal Society, 2007, 463(2078): 321-342.

[13] 林近山. 基于本征时间尺度分解算法的齿轮箱故障诊断[J]. 机械传动, 2011, 35(9): 51-53.

LIN Jinshan. Fault diagnosis of gear box based on intrinsic time-scale decomposition algorithm[J]. Journal of Mechanical Transmission, 2011, 35(9): 51-53.

[14] 杨宇, 王欢欢, 程军圣. 基于ITD改进算法和关联维数的转子故障诊断方法[J]. 振动与冲击, 2012, 31(23): 67-70.

YANG Yu, WANG Huanhuan, CHENG Junsheng. A rotor fault diagnosis method based on ITD improved algorithm and correlation dimension[J]. Journal of Vibration and Shock, 2012, 31(23): 67-70.

[15] Richman J S, Moorman J R. Physiological time-series analysis using approximate entropy and sample entropy[J]. American Journal of Physiology, Heart and Circulatory Physiology, 2000, 278 (6): 2039-2049.

[16] 赵志宏, 杨绍普. 一种基于样本熵的轴承故障诊断方法[J]. 振动与冲击, 2012, 31(6): 136-140, 154.

ZHAO Zhihong, YANG Shaopu. Sample entropy based roller bearing fault diagnosis method[J]. Journal of Vibration and Shock, 2012, 31(6): 136-140, 154

[17] 苏文胜, 王奉涛, 朱泓, 等．基于小波包样本熵的滚动轴承故障特征提取[J]. 振动、测试与诊断, 2011, 31(2): 162-166.

SU Wen-sheng, WANG Feng-tao, ZHU Hong, et al．Feature extraction of rolling element bearing fault using wavelet packet sample entropy[J]. Journal of Vibration, Measurement & Diagnosis, 2011, 31(2): 162-166.

[18] 李锦, 宁新宝. 短时心率变异性信号的基本尺度熵分析[J]. 科学通报, 2005, 50(14): 143821441.

LI Jin, NING Xinbao. The base-scale entropy analysis of short-term heart rate variability signal[J]. Chinese Science Bulletin, 2005, 50(14): 143821441.

[19] Abbasion S, Rafsanjani A, Farshidianfar A, et al. Rolling element bearings multi-fault classification based on the wavelet denoising and support vector machine[J]. Mechanical System and Signal Processing, 2007, 21(7): 2933-2945.

[20] Yuan S F, Chu F L. Fault diagnostics based on particle swarm optimisation and support vector machines[J]. Mechanical System and Signal Processing, 2007, 21(4): 1787-1798.

[21] Rafiee J, Arvania F, Harifi A, et al. Intelligent condition monitoring of a gearbox using artificial neural network[J]. Mechanical Systems and Signal Processing, 2007, 21(4): 1746-1754.

(编辑  陈爱华)

收稿日期：2014-07-01；修回日期：2014-10-14

基金项目(Foundation item)：国家自然科学基金资助项目(51405264，51275273)；三峡大学博士科研启动基金资助项目(KJ2014B040) (Projects (51405264, 51275273) supported by the National Natural Science Foundation of China；Project(KJ2014B040) supported by the Doctoral Scientific Research Foundation of Three Gorges University)

通信作者：钟先友，博士，讲师，从事机械故障诊断、信号分析研究；E-mail: zhxy@ctgu.edu.cn