Heusler合金Ni2MnGa磁性微观机理的第一性原理
吴玉蓉1, 胡望宇1, 赵栋梁2
(1. 湖南大学 应用物理系, 长沙 410082;
2. 北京钢铁研究总院, 北京 100081)
摘 要: 采用量子力学计算软件包研究了单晶Heusler合金Ni2MnGa的结构参数、 磁矩、 四方变形以及磁性微观机理, 并将计算结果与实验值和其它理论计算值进行了比较。 计算所得的结构参数和磁矩相对于局域自旋密度近似值而言, 与实验值符合得更好。 四方变形中, 发现磁矩在c/a=1附近有一个尖锐的最小值, 在c/a≈0.94处有一个局域最大值, 此磁矩的局域最大值对应着一个稳定的马氏体。 总磁矩随c/a的变化主要来自Ni原子: 由于一个原胞中有两个Ni原子对其总磁矩作了贡献, 因而屏蔽了Mn原子的贡献所致。 对总态密度的分析表明, 自旋向上的态密度位于费米面以下, 而自旋向下的态密度有两个主峰, 分别位于费米面两侧, 这是磁有序合金的一个典型特性。 且合金磁性主要源于Mn原子的d-eg和d-t2g亚带, 这与实验结果一致。
关键词: Ni2MnGa; 磁性微观机理; 态密度; 第一性原理 中图分类号: O482.54
文献标识码: A
First-principles of magnetic microcosmic mechanism for Ni2MnGa Heusler alloy
WU Yu-rong1, HU Wang-yu1, ZHAO Dong-liang2
(1. Department of Applied Physics, Hunan University, Changsha 410082, China;
2. Central Iron and Steel Research Institute, Beijing 100081, China)
Abstract: Structure parameters, magnetic moments, tetragonal distortions and magnetic microcosmic mechanisms of single crystal Ni2MnGa Heusler alloy were studied by the vienna abinitio simulation package (VASP). The results show that the structure parameters and magnetic moments agree well with the available experimental data and are better than the local spin density approximation (LSDA) method results compared with the available experiment data and other theoretical values. By analyzing tetragonal distortions, there exists a sharp minimum value near c/a=1 and a local maximum value at c/a≈0.94, and this maximum value corresponds to a stable martensitic phase. In addition, the variation of the total magnetic moment with c/a is mainly due to the contribution of Ni atoms because the total magnetic moment is almost equally contributed by two Ni atoms of per formula unit, while the contribution of Mn atom is very small. By analyzing the total state density (DOS) of alloy, the state densities of major peaks at the majority spin states are below the Fermi level. At the minority spin states, the two major peaks are separated by the Fermi level, which is the characteristic of stability for ferromagnetic ordered alloys. The magnetism of Ni2MnGa alloy mainly originates from Mn atom, and the Mn moment in Ni2MnGa originates from its d-eg and d- t2g sub-bands, which agrees with the experimental results.
Key words: Ni2MnGa; magnetic microcosmic mechanism; states density; first-principle
铁磁性金属间化合物Ni2MnGa具有优良的特性, 如强铁磁性、 大磁致伸缩、 温控和磁控形状记忆效应等, 其磁控形状记忆效应兼具输出应变大、 响应频率快和可精确控制等优点, 引起人们的广泛关注[1-5]。 Ni2MnGa是一种Heusler型合金, 其母相为L21有序立方结构, 点阵参数a=0.5822nm, 合金的磁矩为3.867×10-23A·m2, 且磁性主要来源于Mn原子[6]。 随着温度的降低, 发生马氏体相变, 且在实验过程中已观测到几种稳定的马氏体相, 如5M(c/a〈1)、 7M和非调制体心四方结构马氏体(c/a>1)等[7, 8]。 近几年, 对此合金的研究主要集中在其形状记忆效应和相变上, 理论上对其磁性微观机理的研究还较少。 本文作者采用第一性原理对晶体磁性微观机理进行了分析, 并相应研究了其结构参数、 磁矩和四方变形, 同时将计算结果与实验结果进行了比较。
1 计算方法
采用量子力学计算软件包(vienna abinitio simulation package, VASP)进行计算, 文献[9, 10] 对VASP进行了详细描述。 在本文计算中, 交换相关能用Perdew 和Wang(PW91)[11]所提出的广义梯度近似(generalized gradient approximation, GGA)来处理, 离子和电子间的相互作用采用投影扩充波函数(projector augmented wave, PAW)方法[12]描述, 这是由于对于磁性化合物而言, 投影扩充波函数优于超软赝势(ultra-soft vanderbilt pseudopotentials, US-PP)[13]。 平面波截断能取350eV; k点网孔用Monkhorst-Pack方法产生, 对于原胞取17×17×17; 而对于态密度的计算取23×23×23; 剪切参数取0.2eV; Ni、 Ga和Mn原子占位磁矩分别预取为9.274×10-24、 9.274×10-24和2.782×10-23A·m2。
2 结果与讨论
2.1 晶体结构参数和磁矩
图1所示为Heusler合金Ni2MnGa(L21结构)的结构示意图。 基于此结构, 采用第一性原理所计算的晶格常数、 总磁矩和自旋磁矩以及实验值和其他计算值如表1所列。 在1%的误差范围之内, 本文所计算的晶格常数与实验值基本相符合, 但略小于实验值, 这是由于大多数晶格常数是在室温下测量的。 理论计算的饱和磁矩与实验值也一致, 但小于实验值, 这可能与没有考虑轨道贡献有关。
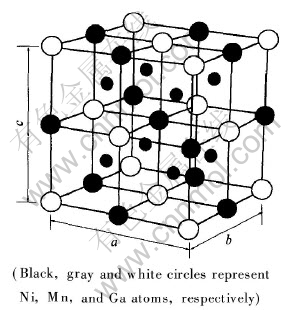
图1 Ni2MnGa fcc L21相的Heusler结构
Fig.1 Heusler structure of fcc L21 phase for Ni2MnGa
表1 理论与实验晶格常数、 总磁矩和自旋磁矩
Table 1 Theoretical and experimental lattice constant, total moment and spin magnetic moment
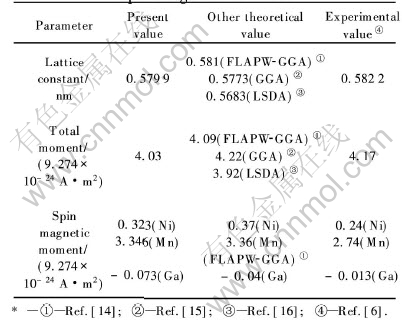
从表1可看出, 本研究所计算的晶格常数和磁矩与Ayuela[14]和Godlevsky等[15]的计算结果基本一致, 但Bungaro等[16]所采用的自旋密度近似计算值小于本研究和其他文献的计算值, 由于Bungaro等的计算对离子和电子间的相互作用采用了球形对称势(atomic sphere approximation, ASA), 这种球形对称势有降低磁性的作用, 而本研究和文献[14, 15]采用了GGA方法, 因此采用ASA方法所得结果小于GGA方法所得结果, 这与文献[17]的结果基本一致。 另外, 铁磁性合金Ni2MnGa磁性主要来源于Mn原子, 同时Ni原子也提供了少量的磁性, 而相对于Ga原子, 它却是反磁性的, 这些都与实验结果相符合。
2.2 四方变形
马氏体相是一种低温相, 在绝对零度附近, 它的能量低于高温相能量。 本文作者研究的为四方结构与L21结构间的变形, 在变形过程中保持晶体的体积不变, 即维持L21结构时的体积。 晶体在发生四方变形时, 总能随c/a的变化而发生相应变化, 其关系如图2所示。 在图2中可清楚发现一个c/a>1的稳定马氏体相, 这与实验结果相符合, 但此马氏体c/a的值约为1.24, 与实验上观察到的这种非调制马氏体c/a的值(为1.18)存在偏差。 但在此图中没有发现另一个c/a〈1的稳定马氏体相, 这可能与计算过程中体积保持不变有关。 由于Ni2MnGa合金在发生马氏体相变时同时伴随着体积收缩, 且此合金稳定结构的存在还与结构调制和原子的错排有关[18]。
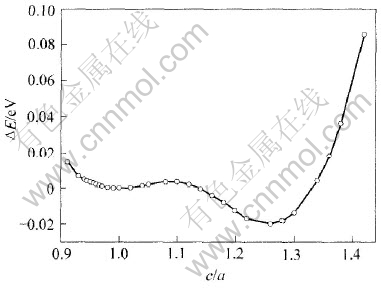
图2 体积保持不变时总能差(相对于L21结构)与c/a的关系
Fig.2 Relationship between total-energy difference (ΔE) and c/a at constant volume (corresponding to L21 phase)
在四方变形中, 总磁矩随c/a的变化而变化。 由图3可看出, 在c/a=1附近有一个尖锐的最小值和在c/a≈0.94处有一个局域最大值, 此局域最大值对应着一个稳定的马氏体相。 在c/a=1附近, Ni的磁矩变化趋势与总磁矩变化相似, 这是由于一个原胞中有两个Ni原子对总磁矩作贡献, Mn原子在此处相似变化被屏蔽所致。 这说明在变形过程中, 总磁矩随c/a变化绝大多数源于Ni原子, 而Mn原子对其贡献较小, 这也与实验结果相一致。
2.3 态密度
图4所示为L21立方结构的总态密度。 由图4可看出, 合金总态密度来源于Ni, Mn 3d 态和Ga 4s态, 且主要来源于Ni和Mn 3d态。 在-10.5~-7.5eV区域内, 态密度主要来源于Ga 4s态, 而Ni和Mn 4s对其贡献比较小。 自旋向上的态密度处于费米能级以下, 自旋向下的态密度存在两个主峰(一个是位于费米能级以下-1.6eV的峰, 另一个是位于费米能级以上1.4eV的峰), 它们分别居
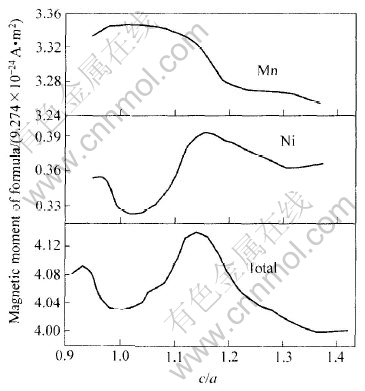
图3 磁矩与c/a的变化曲线
Fig.3 Change curves of magnetic moment with c/a of Ni2MnGa
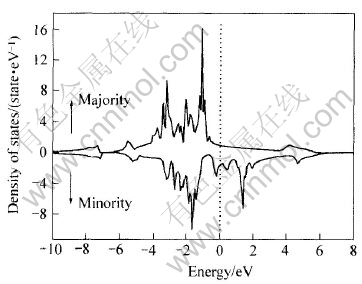
图4 Ni2MnGa总态密度与能量的关系
Fig.4 Relationship between total state density and energy of Ni2MnGa
于费米能级两侧。 这是铁磁有序合金稳定性的一个典型特性, 可用成键轨道和反键轨道间能量分离来解释(已在Ni3Mn的能带结构中进行了描述)[19]。
为了更清楚地了解Ni, Mn 3d态对总态密度的影响, Ni和Mn d分波态密度如图5所示。 由图5可看出, Ni 3d态自旋向上和自旋向下的上部分主要都局限于0~6eV的价带区; 而Mn 3d态的自旋向上部分主要局限于0~6eV的价带区, 自旋向下部分主要局限于费米能级以上0~4eV的导带区。 Ni和Mn d带的自旋向上部分相互交叠, 且它们的d带向上部分几乎是满带。 综合图4和5可知: 总态密度的自旋向下部分有两个峰值, 低能处的峰值主要来源于Ni的d带, 高能处的峰值来源于Mn的d带。 它们以费米能级为界而分开, 且Mn的 d带自旋向下部分几乎是空的。 因此, 合金Ni2MnGa磁矩的携带者主要是Mn原子, 而Ni原子对其贡献比较小, 可以忽略, 这也可从表1得到证实。 为了更清楚地阐明d带特性, 图6和7所示为原子对称投影态密度。 在价带区, Ni的d-eg和d-t2g亚带的自旋向上和自旋向下部分都对Ni原子d态作贡献,而Mn的d-eg和d-t2g亚带只有自旋向上部分对其作贡献, 而自旋向下部分贡献比较小, 因此合金Ni2MnGa中Mn原子磁矩主要源于d-eg和d-t2g亚带。
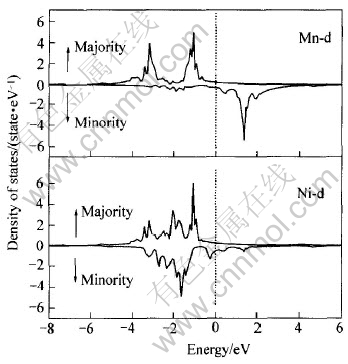
图5 Ni2MnGa 中Ni和Mn的d分波态密度
Fig.5 Spin d electron state densities of Ni and Mn for Ni2MnGa
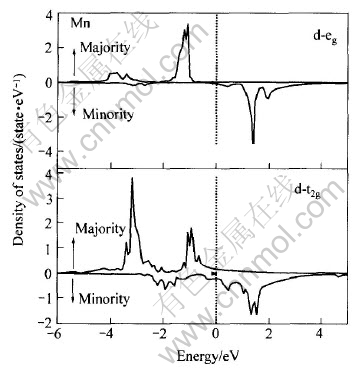
图6 Ni2MnGa中Mn原子对称投影态密度
Fig.6 Symmetry projected state densities of Mn atom for Ni2MnGa
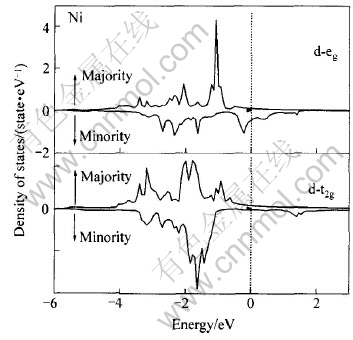
图7 Ni2MnGa中Ni原子对称投影态密度
Fig.7 Symmetry projected state densities of Ni atom for Ni2MnGa
3 结论
1) 应用VASP软件包对Ni2MnGa晶体的结构参数、 磁矩进行了计算, 并与其它理论计算值和实验值进行了比较, 发现它们符合较好。
2) 在四方变形中, 晶体的总磁矩随c/a的变化主要源于Ni的变化, 这是由于一个原胞中有两个Ni原子对总磁矩作贡献, 从而屏蔽了Mn原子的贡献。 在c/a=0.94处存在一个局域最大值, 且此处对应着一个稳定的马氏体相。
3) 合金的磁性源于 Mn原子的d-eg和d-t2g亚带。
REFERENCES
[1]Ullakko K, Huang J K, Kantner C, et al. Large magnetic-field-induced strains in Ni2MnGa single crystals[J]. Appl Phys Lett, 1996, 69: 1966-1968.
[2]Pons J, Chernenko V A, Santamarta R, et al. Crystal structure of martensitic phases in Ni-Mn-Ga shape memory alloys[J]. Acta Mater, 2000, 48: 3027-3038.
[3]Likhachev A A, Sozinov A, Ullakkp K. Different modeling concepts of magnetic shape memory and their comparison with some experimental results obtained in Ni-Mn-Ga[J]. Mater Sci Eng A, 2004, 378: 513-518.
[4]Vovk A, Malkinski L, Golub V, et al. Magnetotransport in NiMnGa thin films[J]. J Appl Phys, 2005, 97:10C50_1-3.
[5]Wan J F, Wang J N. Structure dependence of optical spectra of ferromagnetic Heusler alloy Ni-Mn-Ga[J]. Physica B, 2005,355:172-175.
[6]Webster P, Ziebeck K, Tows S, et al. Magnetic order and phase transformation in Ni2MnGa[J]. Philos Mag, 1984, 49: 295-310.
[7]Kokorin V V, Martynov V V. The crystal structure of thermally and stress-induced martensites in Ni2MnGa single crystals[J]. J Phys Ⅲ France, 1992, 2: 739-749.
[8]Martynov V V. X-ray diffraction study of thermally and stress-induced phase transformations in single crystalline Ni-Mn-Ga alloys[J]. J Physique Ⅳ, 1995, 5: C8, 91-C8, 99.
[9]Kresse G, Furthmüller J. Efficient iterative schemes for ab-initio total-energy calculations using a plane-wave basis set[J]. Phys Rev B, 1996, 54: 11169-11186.
[10]Kresse G, Furthmüller J. Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set[J]. Comput Mater Sci, 1996, 6: 15-50.
[11]Perdew J P, Chevary J A, Vosko S H, et al. Atoms, molecules, solids, and surfaces: Applications of the generalized gradient approximation for exchange and correlation[J]. Phys Rev B, 1992, 46: 6671-6687.
[12]Blchl P E. Projector augmented-wave method[J]. Phys Rev B, 1994, 50: 17953-17979.
[13]Kresse G, Joubert D. From ultrasoft pseudopotentials to the projector augmented-wave method[J]. Phys Rev B, 1999, 59: 1758-1775.
[14]Ayuela A, Enkovaara J, Ullakko K, et al. Structural properties of magnetic Heusler alloys[J]. J Phys: Condens Matter, 1999, 11: 2017-2026.
[15]Godlevsky V V, Rabe K M. Soft tetragonal distortions in ferromagnetic Ni2MnGa and related materials from first principles[J]. Phy Rev B, 2001, 63: 134407-134411.
[16]Claudia B, Rabe K M, Corso A D. First-principles study of lattice instabilities in ferromagnetic Ni2MnGa[J]. Phy Rev B, 2003, 68: 134104-134112.
[17]Mohn P, Blaha P, Schwarz K. Magnetism in the Heusler alloys: Co2TiSn and Co2TiAl[J]. J Magn Magn Mater, 1995, 140-144: 183-184.
[18]Zayak A T, Entel P. Role of shuffles and atomic disorder in Ni-Mn-Ga[J]. Mater Sci Eng A, 2004, 378: 419-423.
[19]Yamashita J, Asano S, Wakoh S. Electronic structure of Ni-Mn alloys[J]. Prog Theor Phys, 1972, 47: 774-789.
(编辑李艳红)
基金项目: 国家自然科学基金资助项目(50371026)
收稿日期: 2005-07-15; 修订日期: 2005-08-20
作者简介: 吴玉蓉(1976-), 女, 博士研究生
通讯作者: 胡望宇, 教授; 电话:0731-8823971; E-mail: wangyuhu2001cn@yahoo.com.cn