Trans. Nonferrous Met. Soc. China 24(2014) 3302-3308

Subsidence prediction method based on equivalent mining height theory for solid backfilling mining

Guang-li GUO^1,2, Xiao-jun ZHU^1,2, Jian-feng ZHA^1,2, Qiang WANG^1,2

1. Key Laboratory for Land Environment and Disaster Monitoring of the State Bureau of Surveying and Mapping, China University of Mining and Technology, Xuzhou 221116, China;

2. Jiangsu Key Laboratory of Resources and Environmental Information Engineering, China University of Mining and Technology, Xuzhou 221116, China

Received 10 July 2013; accepted 6 January 2014

Abstract: Based on the characteristics of strata movement of solid backfilling mining technology, the surface subsidence prediction method based on the equivalent mining height theory was proposed, and the parameters selection guideline of this method was also described. While comparing the parameters of caving mining with equivalent height, the subsidence efficient can be calculated according to the mining height and bulk factor of sagging zone and fracture zone, the tangent of main influence angle of solid backfilling mining is reduced by 0.2-0.5 (while it cannot be less than 1.0). For sake of safety, offset of the inflection point is set to zero, and other parameters, such as horizontal movement coefficient and main propagation angle are equal to the corresponding parameters of caving mining with equivalent height. In the last part, a case study of solid backfilling mining subsidence prediction was described. The results show the applicability of this method and the difference of the maximum subsidence point between the prediction and the observation is less than 5%.

Key words: solid backfilling mining; mining subsidence; equivalent mining height; subsidence prediction; subsidence control

1 Introduction

Subsidence is the most common disaster in mining areas and results in lots of environmental problems, which attracts many researchers to work on this topic. Subsidence control by filling has been explored for hundreds of years, and many methods have been developed [1-6]. However, their performance on filling and subsidence control varies significantly [7-9]. To control the subsidence, an accurate subsidence prediction is crucial for designing the workface, protecting the buildings and selecting optimized mining method. At present, numerical simulation, similar material physics simulation and influence function method are the main ways to predict surface subsidence [10-12]. Among these methods, influence function method is the most widely used one in China with the parameters obtained by plenty of observations [13]. Therefore, the surface subsidence of solid backfilling mining is also predicted based on this method as caving mining except that the subsidence coefficient was decreased to reflect the effect of subsidence relief. Hereby, the subsidence control can be compared intuitively among different filling methods, such as the subsidence coefficient of sand filling and pneumatic filling is 0.05-0.55 [14]. To be specific, the subsidence coefficient depends on geological and mining conditions, filling material, filling rate and other factors [15], which causes the difficulty for determining subsidence coefficient. Hence, it is difficult to fix reasonable parameters for subsidence prediction, especially for the newly developed mining methods, such as solid backfilling mining and cement backfilling mining.

To solve this problem, the concept of equivalent mining height in solid backfilling mining was proposed. In this theory, an assumption that the subsidence basin induced by solid backfilling mining is the same as deformation caused by caving mining with equivalent height. Therefore, the subsidence prediction induced by solid backfilling mining can be switched to predict the deformation induced by caving mining. Then the probability integral method, which is based on influence function theory and widely used for subsidence prediction induced by caving mining in China can be applied. Besides, the equivalent mining height theory is also used for coal pressure and strata deformation analysis in solid backfilling mining technology. In this work, the parameter selection for this method was given as well. Hereby, mining subsidence of solid backfilling mining can be predicted and it will provide a reliable evidence for mining design under buildings, water bodies and railways.

2 Strata movement characteristics of solid backfilling mining

Coal exploitation breaks the stress balance of overlying strata and leads to strata movement and surface subsidence. In the process of strata and surface movement, strata in caving zones and fracture zones break, which reduces the subsidence space effectively, and stops the strata moving [15]. Compared with the caving mining method, the solid filling material occupies most of the space after mining and constrains roof subsidence when the solid backfilling mining is used. This also explains why overlying strata movement and surface subsidence can be controlled effectively by solid backfilling mining.

Based on a large number of experimental results [16], characteristics of overlying strata damage and surface movement in solid backfilling mining can be summarized as follows.

1) No obvious caving zones develop in overlying strata and only small fracture zones form in immediate roof, overlying strata bends as a whole and a tardy basin is formed. The difference of structure and morphology in the overlying strata of caving mining and solid backfilling mining is shown in Fig. 1.

2) Solid filling material is compacted slowly with bending and subsiding of overlying strata. Bearing capability of overlying strata is improved while compaction deformation decreases gradually until it stays in a stable level. There is a great difference in the process of overlying strata subsiding between solid backfilling mining and caving mining. For solid backfilling mining, overlying strata subsides slowly, but for caving mining, the overlying strata subside dramatically.

3) Characteristics of subsidence basin are similar between solid backfilling mining and caving mining method. However, the surface subsidence and deformation of solid backfilling mining is much smaller than caving mining. An apparent deformation and subsidence reduction can be seen for overlying strata. Moreover, uniform and unified subsidence is the most common behaviors for overlying strata of solid backfilling mining while it cannot be seen in caving mining.

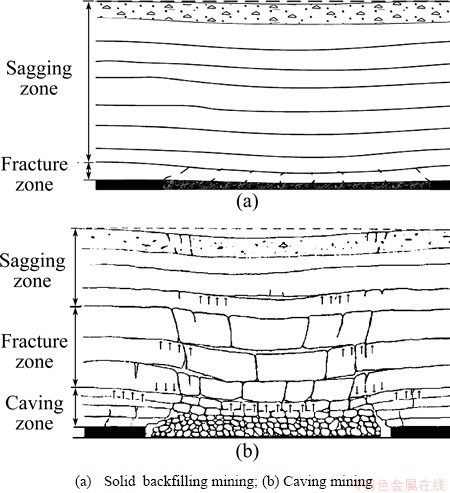
Fig. 1 Overlying rock movement and deformation of caving mining and solid backfilling mining method

3 Connotation of equivalent mining height

Mining height is the dominant factor which affects strata movement and surface deformation. For solid backfilling mining, filling material occupies the goaf and reduces the subsidence space of overlying strata. It also can be explained in this way that the subsidence is caused by mining coal with an equivalent height. To be specific, equivalent mining height is the mining height of filling working face minus the height of filling material after compaction. As shown in Fig. 2, we denote the height of solid backfilling mining as M, and the subsidence of overlying strata roof as M_e. Based on the assumption that the mining subsidence basin is same between solid backfilling mining with its mining height M and caving method with its mining height M_e. Together with the equivalent mining height model, the equation for calculating the equivalent mining height is shown in formula (1).

M_e=h_z+(k-k′)M′h_z                            (1)

where M_e is the equivalent mining height; h_z is the unfilled height in goaf; M is the mining height; k is the initial porosity of the filling material; k′ is the residual porosity after compaction.

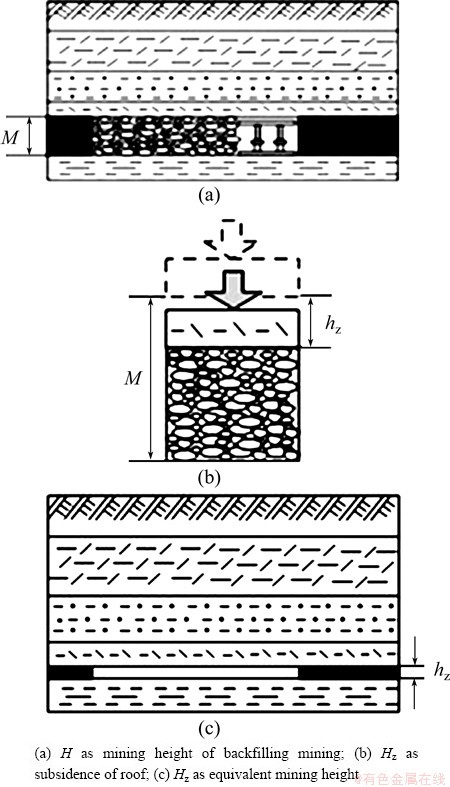
Fig. 2 Equivalent mining height model of backfilling mining

Based on the equivalent mining height theory, all methods used for caving method subsidence prediction can be applied to solid backfilling mining after substituting the mining height to equivalent height. Though many subsidence prediction methods were developed in China [13], the probability integral method is the most widely used subsidence prediction method. Subsidence prediction parameters were also given based on the surface observations. Therefore, the probability integral method was selected for solid backfilling mining subsidence prediction.

4 Determination of parameters of subsidence prediction model

The strata movement mechanism and characteristics of solid backfilling mining are different from those of caving mining. This leads to different values and meanings of probability integral parameters of surface subsidence prediction between solid backfilling mining and caving mining.

Subsidence prediction parameters in probability integral method consist of subsidence coefficient, horizontal movement coefficient, tangent of the main influence angle, offset of the inflection point and main propagation angle. Four methods are available for determining the model parameters: 1) parameters inversion from the measured data; 2) theoretical analysis; 3) analog method; 4) empirical formula method. For solid backfilling mining, the measured data of surface subsidence are quite scarce and the empirical formula is not available. Therefore, it is not feasible for inversing parameters from measured data, analog or empirical formula, and more focus should put on the theoretical analysis on solid backfilling mining.

However, researchers have established a plenty of field observations in China for caving mining and this provides many available parameters of probability integral model. Meanwhile, the subsidence basin is similar between caving mining method and solid backfilling mining method, which makes probability integral model applicable to predict the subsidence of solid backfilling mining method. Therefore, it is necessary to establish the parameter relationship between these two mining technologies. Available results derived from many years’ field observations should be used as well.

The relationship of parameters between solid backfilling mining and caving mining are as follows.

4.1 Subsidence coefficient

Subsidence coefficient (q) is the ratio of the maximum subsidence with mining height under fully extraction and it can be defined as

q=W₀/(Mcos α)                               (2)

For solid backfilling mining, the subsidence coefficient can be defined as

q_z=W₀/(M_ecos α)                              (3)

where q is the subsidence coefficient; W₀ is the maximum subsidence of fully extraction; M is mining height of caving mining; q_z is the subsidence coefficient of solid backfilling mining; M_e is the equivalent mining height of solid backfilling mining, and α is the incidence angle of coal seam.

While considering the definition of subsidence coefficient, the value of it depends on the maximum subsidence. For caving mining, the maximum subsidence is mainly determined by mining height, residual bulking factor of collapse, fracture and sagging zones, which is expressed as

W_c=M_e-H₁(k₁-1)-H₂(k₂-1)-H₃(k₃-1)             (4)

where W_c is the maximum subsidence of caving mining method with the mining height of M_e; H₁, H₂ and H₃ are heights of collapse, fracture and sagging zones, respectively; k₁, k₂ and k₃ are bulking factors of collapse, fracture and sagging zones correspondingly.

Thus, the mining depth can be approximately expressed by H=H₁+H₂+H₃.

The overlying strata subsides slowly under the support of filling in solid backfilling mining, fracture and sagging zones develop and the corresponding maximum subsidence can be expressed as

W_z=M_e-H′₂(k′₂-1)-H′₃(k′₃-1)                   (5)

The mining depth of solid backfilling mining can be described as H=H′₂+H′₃, where W_z is the maximum subsidence by solid backfilling mining; H′₂, H′₃ are the heights of fracture zone and sagging zone, respectively; k′₂, k′₃ are the bulking factors of fracture and sagging zone correspondingly.

Figure 3 shows the comparison of vertical residual bulking factor in strata of caving mining with equivalent mining height and solid backfilling mining which is obtained by analyzing the similar material simulation results. Results show that the bulking factors in sagging and fracture zones of solid backfilling mining and caving mining with equivalent mining height are small, and the difference between these two mining methods is not apparent. Hereby, we can assume that the residual bulking factors in fracture and sagging zones are similar for caving mining with equivalent mining height and solid backfilling mining.

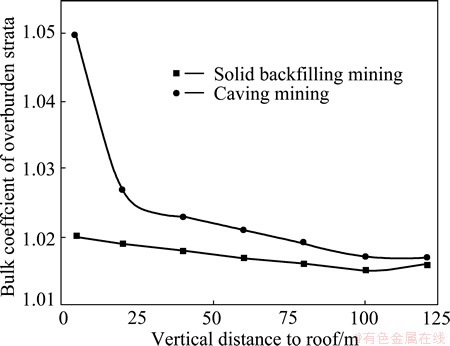
Fig. 3 Vertical residual bulking factor between caving mining and solid backfilling mining

To sum up the analysis above, it can approximately assume that the residual bulking factors of fracture and sagging zones of overlying strata in solid backfilling mining are equal to the corresponding coefficients in caving mining. Hereby, formula (5) can be changed to

W_z=M_e-H′₂(k₂-1)-H′₃(k₃-1)                   (6)

By comparing Eqs. (5) and (6), it can be seen that the difference of the maximum subsidence between caving mining (with the height M_e) and solid backfilling mining (with the mining height M) is

W_z-W_c=H₁(k₁-1)-H₂(k₂-1)-H₃(k₃-1)-H′₂(k₂-1)- H′₃(k₃-1)         (7)

Correspondingly, the difference of subsidence coefficient between different mining methods is

q_z-q_c=[H₁(k₁-1)+(H₂-H′₂)(k₂-1)+(H₃-H′₃)(k₃-1)]/M_e    (8)

According to Eq. (8), the subsidence coefficient of solid backfilling mining can be expressed as

q_z=q_c+Δq= q_c+ [H₁(k₁-1)+(H₂-H′₂)(k₂-1)+(H₃-H′₃)(k₃-1)]/M_e         (9)

In practical application, heights of collapse zone (H₁) and fracture zone (H₂) of caving mining can be calculated according to the empirical formula, and the bulking factors of collapse (k₁) and fracture (k₂) zones can be measured by cylinder compression test [16]. Then, based on the subsidence coefficient of caving mining and Eq. (5), k₃ can be calculated. By substituting k₃ into Eq. (9), the subsidence coefficient of solid waste filing q_z can be fixed.

According to the previous illustration, several conclusions related to subsidence coefficient q are obtained.

1) Subsidence coefficient of caving mining and solid backfilling mining decreases slightly when the mining height increases, and the difference between them increases gradually with increment of mining height.

2) While the mining height is small (less than 0.5 m), subsidence coefficients under these two conditions are almost the same.

3) With the increase of mining depth, the proportion of bedrock thickness also increases. This implies that the overlying strata becomes harder and the subsidence coefficient for caving mining and solid backfilling mining decreases, and the magnitude of decrease of solid backfilling mining is smaller than that of caving mining.

4) While the mining depth increases, the difference for subsidence coefficient of caving mining and solid backfilling mining increases; it decreases when subsidence coefficient for caving mining increases(when the comprehensive lithology for overlying strata is soft) and vice versa.

4.2 Tangent of main influence angle (tan β)

Tangent of the main influence angle (tan β) is a parameter which reflects the range of inside and outside border of surface movement basin, it mainly shows the concentration of surface movement after it reaches a stable state. According to the surface movement observations in China, tangent of the main influence angle under caving mining is related to the lithology of overlying strata, mining depth and incidence angle of coal seam. When strata become harder or incidence angle of coal seam increases, tan β becomes smaller; while the mining depth increases, tan β increases as well. In general, the value of tan β ranges from 1.2 to 1.6.

Compared with caving mining, characteristics of overlying strata movement of solid backfilling mining is quite different. For this technique, collapse and fracture zones are not been developed and the failure height of overlying strata is much smaller. So the tangent of main influence angle is small since its lithology is harder than that of caving mining.

Similar material simulation results [16,17] show that tangent of main influence angle of solid backfilling mining is smaller than that of caving mining with the magnitude of 0.2-0.5. Thus, it is highly recommended that for determining the tangent of main influence angle of probability integral method in solid backfilling mining based on equivalent mining height, we should subtract 0.2 to 0.5 from the tangent of main influence angle of caving mining. However, it should be noticed that the tangent value of main influence angle cannot be less than 1.0.

4.3 Offset of inflection points

For caving mining, cantilevers and cavities are formed at the boundary of goaf and the space reduced for collapsed strata moves, which decrease the size of goaf. In order to predict surface movement accurately, the offset of the inflection point is introduced. In general, the offset of the inflection point increases while the lithology becomes harder.

For solid backfilling mining, equivalent mining height is the virtual height and inflection points do not have the physical meaning as caving mining. The inflection points should be treated with the non-compressed length of the filling material at boundary of goaf. Overlying strata subsides slowly under the protection of filling material, then, the underground pressure of working face becomes smaller and the overlying strata becomes more difficult to be broken. The offset of the inflection point should increase compared with caving mining. But in the view of safety, the offset of the inflection point can be determined as the same as caving mining or be set to 0 in the process of subsidence prediction of solid backfilling mining.

4.4 Horizontal movement coefficient

The horizontal movement coefficient (b) is the ratio between the maximum horizontal and vertical movement, and it depends on the thickness of alluvium layer and incidence angle of coal seam. For solid backfilling mining and caving mining, their horizontal movement coefficients are at the same level approximately.

4.5 Main propagation angle

Main propagation angle (θ₀) is the parameter which reflects surface movement and deformation prediction in dip direction while mining with tilt coal seams. The main propagation angle relates to the incidence angle of coal seam mostly. For the values of main propagation angle in solid backfilling mining and caving mining, they are at the same level and it can be described as follows:

θ₀=90°-kα                                  (10)

where k is a constant (less than 1.0), and k ranges from 0.7 to 0.8, from 0.6 to 0.7 or 0.5 to 0.6 under different conditions of hard, medium-hard, and soft overlying strata, respectively.

5 Case study

Huayuan coal mine is located in Jinxiang county, Ji’ning city, Shandong province. The research area is the 2# panel of Huayuan coal mine. Many villages and different lands are above the panel as shown in Fig. 4.

Fig. 4 Villages and lands above 2# panel

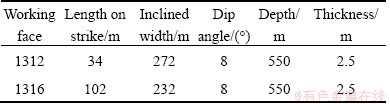
In order to protect the houses and important buildings on the surface, solid backfilling mining was selected for mining coal in the 2# panel(1312 and 1316 working faces are included). The overview of 1312 and 1316 is listed in Table 1.

Table 1 Overview of 1312 and 1316 work faces

Subsidence prediction based on the proposed method was performed to evaluate the subsidence damage after 1312 and 1316 working faces’ exploitation. Parameters of probability integral method for thin coal seam in Huayuan coal mine are listed as follows: subsidence coefficient, 0.94; tangent of main influence angle, 1.6; offset of the inflection point, 0.05H; main propagation angle of extraction, 90-0.4α.

According to the method for parameters selection referred above and considered with plenty of numerical simulation results, the parameters for solid backfilling mining method in Huayuan coal mine are refined as follows: subsidence coefficient, 0.97; tangent of main influence angle, 1.3; offset of the inflection point, 0; main propagation angle of extraction, 90-0.4α.

By cylinder compression method [89], the compression characteristics of solid waste in Huayuan coal mine is tested, and the equivalent height, which equals 572 mm, was given through formula (1). Later on, the surface subsidence after 1312 and 1316 working faces’ exploitation was calculated through the self-made software program.

Meanwhile, monitoring station of surface movement was also set during the 1312 and 1316 mining process, and the surface subsidence was surveyed from 2011-04-12 to 2012-10-17 with one month interval. In total, five survey lines were set on the surface, and the difference of survey line B between the measured data and predicted data is shown in Fig. 5.

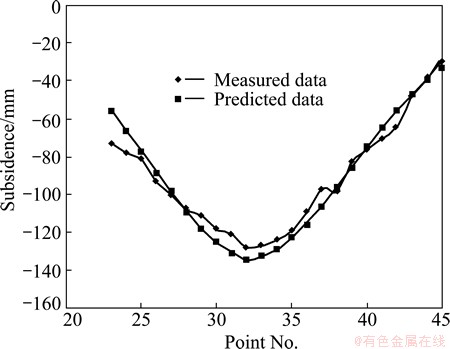
Fig. 5 Subsidence comparison between measured and predicted data of survey line B

It can be seen in Fig. 5 that the prediction subsidence distribution is similar with measured data. The error of the maximum subsidence point is smaller than 5%. Similar conclusions can be obtained through other four survey lines. Thus, it can be concluded that the probability integral method based on the equivalent height theory can be used for the subsidence prediction of solid waste mining method.

6 Conclusions

1) For solid backfilling mining, the overlying strata move tardily and slowly. Fracture and sagging zones are developed. The subsidence basin of this technology is similar with the basin of caving mining with equivalent height.

2) The equivalent height theory was proposed. It assumes that the subsidence basin of solid backfilling mining is the same as the deformation induced by caving mining with equivalent height. Hereby, it is reasonable for switching solid backfilling mining subsidence prediction to calculate the deformation of caving mining with equivalent height, and the widely used probability integral method in China can be applied to solid backfilling mining subsidence prediction.

3) The parameter selection method for solid backfilling mining subsidence prediction was also brought forward. Subsidence coefficient can be calculated according to the height and bulk factor of sagging and fracture zones. The tangent of main influence angle is reduced by 0.2-0.5 from caving method with the equivalent mining height (but it cannot be less than 1.0). Offset of the inflection point is set to zero for safety; other parameters, such as horizontal movement coefficient and main propagation angle of solid backfilling mining, are equal to the corresponding parameters of caving method with equivalent mining height.

4) Case study results show that the subsidence induced by solid backfilling mining can be predicted by probability integral method with equivalent mining height, and the error of the maximum subsidence point is less than 5%.

References

[1] GUO Guang-li, FENG Wen-kai, ZHA Jian-feng, LIU Yuan-xu, WANG Qiang. Subsidence control and farmland conservation by solid backfilling mining technology [J]. Transactions of Nonferrous Metals Society of China, 2011, 21(S3): s665-s669.

[2] ZHANG Ji-xiong, ZHOU Nan, HUANG Yan-li, ZHANG Qiang. Impact law of the bulk ratio of backfilling body to overlying strata movement in fully mechanized backfilling mining [J]. Journal of Mining Science, 2011, 47(1): 73-84.

[3] GUO Guang-li, ZHA Jian-feng, MIAO Xie-xing, WANG Qiang, ZHANG Xian-ni. Similar material and numerical simulation of strata movement laws with long wall fully mechanized gangue backfilling [J]. Procedia Earth and Planetary Science, 2009(1): 1089-1094.

[4] YAO Yuan, CUI Zeng-di, WU Ru-zhou. Development and challenges on mining backfill technology [J]. Journal of Materials Science Research, 2012, 1(4): 73-78.

[5] HUANG Yan-li, ZHANG Ji-xiong, ZHANG Qiang, NIE Shou-jiang. Backfilling technology of substituting waste and fly ash for coal underground in China coal mining area [J]. Environmental Engineering and Management Journal, 2011, 10(6): 769-775.

[6] MIAO Xie-xing. Progress of fully mechanized mining with solid backfilling technology [J]. Journal of Coal Science & Engineering (China), 2012, 37(8): 1247-1255. (in Chinese)

[7] FENG Guang-ming, JIA Kai-jun, LI Feng-kai, YIN Shu-ming, WANG Hong-hai. Research on overburden strata control using a super high water content material during open back fill mining [J]. Journal of China University of Mining and Technology, 2011, 40(6): 841-845. (in Chinese)

[8] XU Jia-lin, YOU Qi, ZHU Wei-bing, LI Xing-shang, LAI Wen-qi. Theorectical study of strip-filling to control mining subsidence [J]. Journal of China Coal Society, 2007, 32(2): 119-122. (in Chinese)

[9] CHEN Shao-jie, GUO Wei-jia, ZHOU Hui, WEN Guo-hui. Structure model and movement law of overburden during strip pillar mining backfill with cream-body [J]. Journal of China Coal Society, 2011, 36(7): 1081-1086. (in Chinese)

[10] LUO Yi, CHENG Jian-wei. An influence function method based subsidence prediction program for longwall mining operations in inclined coal seams [J]. International Journal of Mining Science and Technology, 2009, 19(5): 592-598.

[11] XIE He-ping, ZHOU Hong-wei, WANG Jing-an, LI Long-zhong. Application of FLAC to predict ground surface displacements due to coal extraction and its comparative analysis [J]. Chinese Journal of Rock Mechanics and Engineering, 1999, 5(4): 29-33. (in Chinese)

[12] GAO Feng, ZHOU Ke-ping, DONG Wei-jun, SU Jia-hong. Similar material simulation of time series system for induced caving of roof in continuous mining under backfill [J]. Journal of Central South University of Technology, 2008, 15(3): 356-360.

[13] Industry, National Ministry of Coal. Coal pillar design and mining regulations under buildings, water, railways [M]. Beijing: China Coal Industry Press, 2005. (in Chinese)

[14] ZOU You-feng, DENG Ka-zhong, MA Wei-min. Mining subsidence engineering [M]. Xuzhou:China University of Mining and Technology Press, 2003. (in Chinese)

[15] WANG Lei, ZHANG Xian-ni, GUO Guang-li, ZHA Jian-feng. Quality control system framework for fully mechanized mining [J]. Journal of China Coal Society, 2013, 38(9): 1568-1575. (in Chinese)

[16] ZHA Jian-feng. Study on the foundational problems of mining subsidence controlled in waste stow [D]. Xuzhou: China University of Mining and Technology, 2008. (in Chinese)

[17] HU Bing-nan, GUO Ai-guo. The Compression simulation experiment research of coal wasting filling material [J]. Journal of Coal Science & Engineering (China), 2009, 34(8): 1076-1080.

基于等价采高理论的固体充填采煤沉陷预计方法

郭广礼^1,2，朱晓峻 ^1,2，查剑锋 ^1,2，王 强^1,2

1. 中国矿业大学 国土环境与灾害监测国家测绘地理信息局重点实验室，徐州 221116；

2. 中国矿业大学 江苏省资源环境与信息工程重点实验室，徐州 221116

摘  要：在分析固体充填采煤岩层移动特征的基础上，提出固体充填采煤沉陷预计方法，并给出概率积分法参数选取方法。研究认为：与等价采高煤层垮落法开采下沉系数相比较，固体充填采煤沉陷预计参数中下沉系数可以根据垮落带、裂隙带的高度以及碎胀率计算得出；主要影响角的正切略小0.2~0.5，但不应小于1.0；出于安全考虑，拐点偏移距离可为零；水平移动系数和下沉影响角可不变。最后，利用基于等价采高理论的概率积分法模型计算了花园煤矿固体充填的地表沉陷。结果表明，该方法较为可靠地预测了固体充填的地表沉陷，最大下沉点的预计误差不超过5%。

关键词：固体充填采煤；开采沉陷；等价采高；沉陷预计；沉陷控制

(Edited by Xiang-qun LI)

Foundation item: Project (2012BAB13B03) supported by the National Scientific and Technical Supporting Programs Funded of China; Project (41104011) supported by the National Natural Science Foundation of China; Project (2013QNB07) supported by the Natural Science Funds for Young Scholar of China University of Mining and Technology; Project (2012LWB32) supported by the Fundamental Research Funds for the Central Universities, China

Corresponding author: Jian-feng ZHA; Tel: +86-516-83591307; E-mail: zha_jf@163.com

DOI: 10.1016/S1003-6326(14)63470-1