J. Cent. South Univ. (2019) 26: 3103-3113

DOI: https://doi.org/10.1007/s11771-019-4239-8

Fourier-shape-based reconstruction of rock joint profile with realistic unevenness and waviness features

NIE Zhi-hong(聂志红)¹, WANG Xiang(王翔)¹, HUANG Dong-liang(黄栋梁)¹,ZHAO Lian-heng(赵炼恒)^{1, 2}

1. School of Civil Engineering, Central South University, Changsha 410075, China;

2. Key Laboratory of Heavy-haul Railway Engineering Structure (Ministry of Education),Central South University, Changsha 410075, China

Central South University Press and Springer-Verlag GmbH Germany, part of Springer Nature 2019

Abstract: Rock joint shape characteristics, waviness and unevenness play essential but distinct roles in shear mechanism of rock joints. This study presents a novel method to generate virtual rock joint profiles with realistic waviness and unevenness features. Firstly, joint profiles are obtained by 3D laser scanning device. Secondly, quantification of waviness and unevenness is conducted by traditional method, including digital filtering technique and roughness parameter R_L. Thirdly, the discrete Fourier transform (DFT) method is employed to analyze the joint outlines. Two representative Fourier shape descriptors (D₃, D₈) for characterization of waviness and unevenness are suggested. Then, the inverse discrete Fourier transform (IDFT) is adopted to reconstruct the joint profiles with random values of phase angles but prescribed amplitudes controlled by D₃ and D₈. The traditional method is then applied to the reconstructed joint profiles to examine statistically the relationships between D₃ and D₈ and parameters R_L of waviness and unevenness, respectively. The results show that larger D₈ tends to result in larger waviness while higher D₃ tends to increase unevenness. Reference charts for estimation of waviness and unevenness with different pairs of D₃ and D₈ are also provided to facilitate implementation of random joint reconstruction.

Key words: rock joint profile; joint shape analysis; discrete Fourier transform; joint reconstruction

Cite this article as: NIE Zhi-hong, WANG Xiang, HUANG Dong-liang, ZHAO Lian-heng. Fourier-shape-based reconstruction of rock joint profile with realistic unevenness and waviness features [J]. Journal of Central South University, 2019, 26(11): 3103-3113. DOI: https://doi.org/10.1007/s11771-019-4239-8.

1 Introduction

Rock joint shape has been regarded as one of the most important factors that affect both the mechanical and hydraulic properties of jointed rock mass. Through both laboratory experiment and numerical modeling, numerous studies have been conducted by many researchers to investigate the evolution of joint surface morphology during shearing [1-4] and the mechanisms [5-9] that how the joint shape may affect the macroscopic properties of the rock joints. Among all these previous comprehensive works, the joint roughness coefficient (JRC) [10] has been widely employed to represent the irregular shape of the joint profile geometry. Since only standard charts were provided for designers to estimate the joint roughness coefficient (JRC) values by visual comparison, many researchers started to seek for quantitative and non-subjective method to evaluate the JRC values with statistical tools [4]. Univariate statistical parameters, e.g., the root mean square roughness height values RMS, the mean square root Z², the structure function SF, average roughness angles i_ave and roughness profile indexes R_p [11-13] were formulated and correlated with the JRC values of the standard joint profiles provided by BARTON et al [10]. Other approaches, e.g., θ^*_max/(c+1) [14], geostatistical parameters [15], and fractal dimension [16] were also proposed to establish new roughness estimators.

Although these existing parameters can be employed as alternative tools to automatically quantify the rock joint shape with well-correlated JRC value, they were not able to distinguish different scales of joint surface irregularities such as waviness (large scale undulation) and unevenness (small scale roughness) which have been recommended by International Society of Rock Mechanics [17]. As revealed by BANDIS et al [18], the waviness and unevenness shape features play different roles in macroscopic behaviors of rock joint. The waviness, noted as the large-scale roughness, tends to result in the dilation of rock joint under shearing while the unevenness, noted as the small-scale roughness, will possibly cause degradation of shearing surface. Several works have been conducted to discuss these mechanisms. HONG et al [19] performed a series of direct shear tests on artificial rock joints under different confining stress levels to investigate the degradation features and scale of unevenness on sheared rock joint surfaces. HENCHER et al [20] discussed the contributions of the first and second order roughness features to the shear strength of rock joints at project scale. OH et al [21] and LI et al [9] developed a constitutive model to correlate the small-scale roughness (determined from laboratory data) and large-scale waviness (determined from geologic observations) with the dilation and strength of rock joints. Consequently, it is of great importance to distinguish these two roughness features at different geometrical scales to facilitate quantification of the relative contributions of waviness and unevenness to rock joint shear strength. Possible solution was proposed by HONG et al [22] who employed the digital filtering technique combined with the modified roughness shape parameters to quantify the joint unevenness and roughness at two distinct observation levels. However, these statistical parameters cannot be directly utilized to reconstruct the target profiles for numerical modeling of rock joint. Although attempts have been conducted by some researchers to establish the virtual rock joint models with regular zigzag shape outlines [22], random Gaussian noise generated joint profiles [23], fractal interpolation curve [24] and digital library of scanned realistic joint profiles [25, 26], it remains difficult to not only precisely characterize the rock joint waviness and unevenness shapes but also incorporate their effects into the numerical modeling of rock joints in a quantifiable and verifiable way.

To solve the above problems, the quantitative joint profile analysis and random shape reconstruction are introduced based on the discrete Fourier transform (DFT) and inverse discrete Fourier transform (IDFT), respectively. The proposed works are inspired and learned from several researches about irregular shape quantification and reconstruction using spectral analysis methods (e.g., fracture profile roughness measurement [27, 28] based on fast Fourier transform (FFT) and particle shape reconstruction [29-31] based on inverse discrete Fourier transform (IDFT). The relationships between both the harmonic amplitudes and phase angles versus the frequency number are studied to proposed two representative Fourier shape descriptors. Focus is placed here on the correlations between the existing waviness and unevenness shape parameters with the Fourier shape descriptors for virtual joint profile reconstruction.

2 Acquisition of rock joint profiles by laser scanning

Since the instrument resolution is of great importance to the computation stability of rock joint shape characteristics, the non-contact approaches, including the analytical photogrammetric method, He–Ne laser beam technique, laser scanning method and white-light fringe technology, have been widely used to increase the speed and accuracy of roughness measurements. In this study, the 3D laser scanning method, as an advanced automatic three-dimensional morphology scanning technique with high resolution, is employed to digitize the entire rock joint surfaces. The working theory of this method is to measure the spatial distance based on the triangulation mechanism. In this system, the laser dot, the camera and the laser emitter form a triangle. Firstly, the laser emitter sends out the laser light to the surface of the subject. A charge-coupled device (CCD) camera is equipped to receive the reflections at the other side. The angle of the laser emitter corner and the distance between the camera and the laser emitter is recorded. Once the angle of the camera corner is computed by finding the location of the laser dot in the camera's field of view, the shape and size of the triangle together with the location of the laser dot corner of the triangle can then be obtained. The 3D laser scanning system adopted in this study is named as Handy Scan 700 TM, with an accuracy of ±30 μm over a region of 100 mm×100 mm×50 mm in a measuring frequency of 480000 s^-1. Seven beams of laser lights are emitted to scan the target joint surface. With the aid of software VXelements, x, y and z coordinates of the spots can be obtained to form the entire three-dimensional joint surface. The example scanning object and the obtained corresponding digital model are shown in Figure 1. As shown in the figure, the 3D triangular meshes of the joint surface are obtained using the 3D laser scanning technique.

By MATLAB programming, the 2D joint profiles are then obtained by cutting the 3D joint surface along both the longitudinal and transverse directions of the specimen at the inter-profile intervals of 5 mm, as shown in Figure 2. The acquired 2D profiles were digitized into constant data point interval of 0.1 mm. Finally, total 50224 two-dimensional profiles were obtained from the laser scanned 27 pieces of rock joint specimen. The sample profiles will be employed to investigate the statistical results of Fourier-based joint shape analysis.

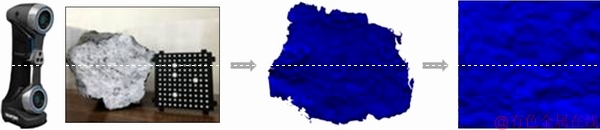
Figure 1 Laser scanning of rock joint surface

3 Traditional waviness and unevenness descriptors

The traditional method for quantification of waviness and unevenness was suggested by HONG et al [22]. It includes roughness classification with digital filtering technique and waviness and unevenness assessment with roughness parameter R_L.

1) Roughness classification. The digital filter is a popular technique in signal processing. In contrast to the electronic filter that operates on continuous-time analog signals, the digital filter is employed to weaken or strengthen certain aspects of the signal sampled in a discrete time domain by performing mathematical operations. The high-pass filters (HPF) are used to pass the signals with frequency components higher than a certain cutoff frequency while low-pass filters (LPF) are used to suppress high-frequency components. Subsequently, the joint profiles were transformed into a frequency domain and classified into waviness (low-frequency components) and unevenness profiles (high- frequency components) at the cut-off frequency of f₀. Following HONG et al [22], f₀ is selected as 0.3 Hz. Figure 3 shows typical results for the shape classification of one example joint profile transformed into waviness and unevenness, respectively.

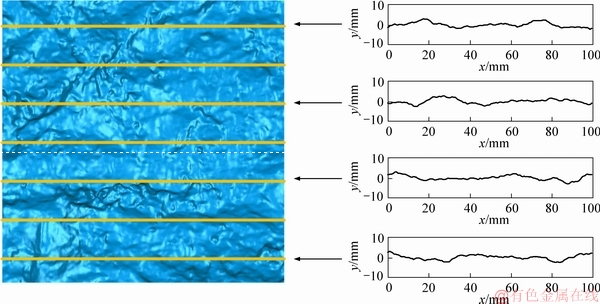
Figure 2 Obtaining 2D joint outlines from 3D joint surface

2) Assessment of waviness and unevenness. After roughness classification, the profile roughness parameter is adopted to evaluate the degree of waviness and unevenness features. R_L is defined as the ratio of profile length reflected on the horizontal surface (L₀) to the length of the actual profile (L). It can be computed by Eq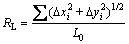. (1):

                       (1)

where Δx_i and Δy_i are increments of the same x and y directions as the shearing direction, respectively; L₀ is the sum of profile length increments reflected on the horizontal surface.

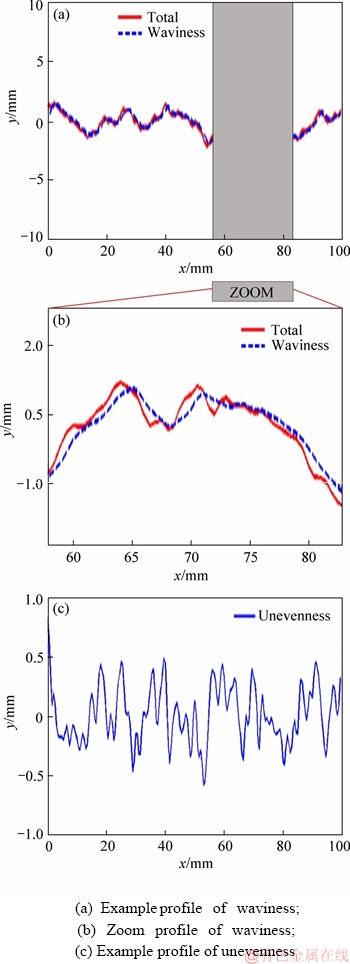
Figure 3 Digital filtering result for shape classification of joint profile (after HONG et al [22]):

4 Fourier shape analysis of rock joint profile

4.1 Discrete Fourier transform of joint outline data

Discrete Fourier transform (DFT), as a basic spectral analysis tool, has been extensively used in shape analysis of irregular geometrical outlines as periodic signals by many researchers [29, 32, 33]. In this study, the 2D rock joint outline can also be regarded as a one-dimensional time-domain signal by properly aligning the joint outline to the x-axis in Cartesian coordinate system, following the steps as below, shown in Figure 4.

Figure 4 Pre-processing of joint outline

Step 1: The profile (in black) is discretized by N_P points separated by a constant interval Δx₀. A straight line (in red) that has the minimum distances from all the discrete points is computed and regarded as the mean surface of the joint profile.

Step 2: Locate the joint profile in a Cartesian coordinate where the alignment of the mean straight line is parallel to the x-axis. Shift the joint profile along the y-axis until the y value of the mean straight line is equal to the prescribed value y′. In this study, considering the scale effect, y′ is selected based on the actual profile length (L) of the rock joint as follows:

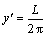                                  (2)

Then, each point P_i can be represented in x-y Cartesian coordinate system as P_i(x_i, y_i). The whole profile is then regarded as a one-dimensional discrete signal in time domain. Based on the Fourier spectrum analysis theory, the discrete signal {P_i(x_i, y_i)} can be transformed into Fourier series as follows:

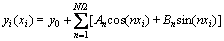         (3)

where y₀ is the average value of all y_i (see Eq. (4)); N is the total number of discretized points; n is the harmonic number which determines the frequency of each harmonic; {A_n, B_n,} is the Fourier spectrum which determines the amplitude of the harmonic (see Eqs. (5) and (6)).

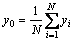                              (4)

                       (5)

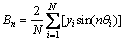                       (6)

It should be noted that this method is only suitable when all half-lines arising from x-axis cross the joint profile exactly one time. Since a majority of the natural joint profiles fulfills this condition, the proposed DFT method should be applicable for most of the cases. Subsequently, Eq. (3) is nominalized by y₀ to transform the time domain signal D_n(φ_n) into frequency domain signal y_i(x_i) (see Eq. 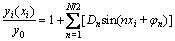(7)).

                (7)

where D_n is defined as the normalized amplitude for harmonic n (see Eq. (8)); φ_n is defined as the phase angle for harmonic n (see Eq. (9)).

                            (8)

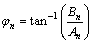                            (9)

The physical meanings of D_n and φ_n are illustrated in Figure 5. Essentially, the time-domain signal {P_i(x_i, y_i)} is decomposed into various sinusoidal signals of different frequencies f=2π/n and amplitudes D_n starting at different phase angle φ_n by discrete Fourier transform (DFT). The normalized amplitude D_n determines the amplitude of the nth superimposed sinusoidal wave while phase angle φ_n determines the starting point that the nth sinusoidal wave is superimposed onto the signal.

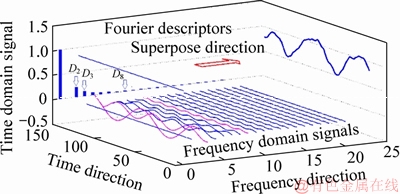
Figure 5 Diagram of discrete Fourier transform after Ref. [30]

4.2 Relations between frequency with amplitude and phase angle

The Fourier-based morphological characterization hypothesis was formulated by MELOY [32] that the shape characteristics of “irregular outline signatures” are dependent on the Fourier amplitudes {D_n} and not on the phase angles {θ_n}. Further investigations show that there is a linear functional relationship between amplitudes {D_n} and n (the frequency of the nth component harmonic) in a log-log scale for irregular particle outline. It is the purposes of this section to examine whether these hypothesizes are also applicable to joint outline.

The statistical relations between n frequency of the nth component harmonic with D_n amplitudes and φ_n phase angles are investigated respectively. The box plots of D_n and φ_n versus n are shown in Figures 6 and 7. The results shown from the figures demonstrated that the amplitudes D_n have a trend of decay towards increasing value of harmonic frequency n (for n≥3) while the mean values of phase angles fluctuated randomly. These findings are consistent with the previous researchers [32, 33]. Subsequently, the results of Fourier amplitudes D_n are further investigated in the following section.

4.3 Experimental regression of amplitudes

To further quantify the relations between D_n and n, the log values of mean amplitudes D_n versus the log value of frequency n are plotted in Figures 8 and 9. It is obvious that, within certain ranges (for n≥3), the log values of amplitudes D_n decrease linearly with the log values of frequency n. Several conclusions are drawn and listed as below:

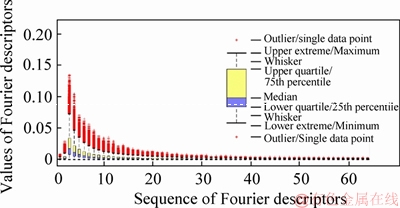
Figure 6 Box plot of Fourier amplitudes

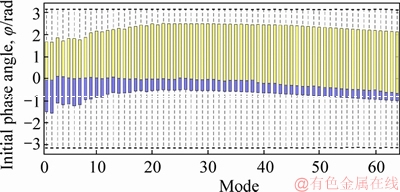
Figure 7 Box plot of phase angles

1) D₁ is close to zero, as shown in Figure 6, and not correlated with other amplitudes. As discussed by MOLLON et al [29], D₁ corresponds to the shift of the signal contour with respect to the reference point and can be set to zero if the position of the signal contour is chosen properly.

2) D₂ is minor, as shown in Figure 6, and has neglected relationship with other amplitudes. As discussed by MOLLON et al [29], D₂ affects the overall aspect ratio of the reconstructed particle outline which is insignificant in the statistical results of the sampled rock joints.

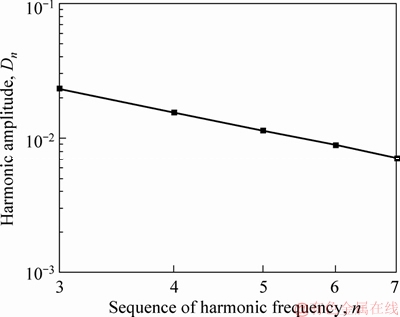
Figure 8 Evolution of mean harmonic amplitude D_n towards frequency n at log scale (3≤n<8)

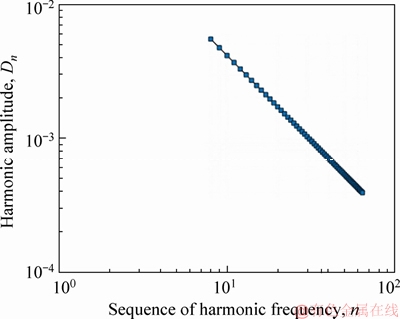
Figure 9 Evolution of mean harmonic amplitude D_n towards frequency n at log scale (8≤n<64)

3) When 3≤n<8, D_n has linear relations with n in log-log sale coordinate (see Eq. (10)).

4) When 8≤n, D_n has similar linear relations with n in log-log sale coordinate (see Eq. (11)).

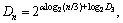3≤n<8                (10)

8≤n                  (11)

where α=-1.4242 and β=-1.3489, computed by linear regression, similar principles that have been employed in the authors previous works [30, 31].

The results obtained above are similar to the previous works done by MOLLON et al [29], in which the discrete Fourier transform was employed to examine the outline contour of the granular particle in a polar coordination system. According to their findings, D₃ and D₈ are more correlated to the intermediate scale and microscopic scale irregularities of the particle outline, respectively. Thus, in this study, based on the above results, two significant and representative harmonic amplitudes D₃ and D₈ are selected as Fourier shape parameters for quantification of joint shape characteristics. The relations between the proposed D₃ and D₈ with the roughness parameters R_L will be statistically analyzed in the next section.

5 Reconstruction of virtual rock joint specimen

The well-established relations between the shape features (unevenness and waviness) with the proposed Fourier shape descriptors make it possible to perform the inverse discrete Fourier transformation (IDFT) operation, i.e. to generate a relevant and realistic population of rock joints with prescribed waviness and unevenness features.

5.1 Generation of rock joint profile by inverse discrete Fourier transform

In order to generate realistic joint profile models with different appearances, some randomnesses need to be introduced in the joint reconstruction process. Since the previous section has proved that the rock joint shape is independent on the spectrum phase angles {φ_n}, it is possible to randomly assigning a phase angle φ_n to each spectrum mode following a uniform distribution on the interval [-π, π]. The discretized outline of the objective rock joint can be obtained using Eq. (3), with:

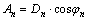                            (12)

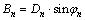                            (13)

Examples of joint profiles generated by the proposed method are presented in Figure 10, each of which follows the amplitude spectrum provided in Figure 4. It is clear from the the figure that the random phase angles lead to different appearances of y_i(x_i) signals (joint profiles) but similar shape features (e.g., the amplitude and the frequency of the irregularities in waviness and unevenness) which are easily identifiable. Figure 11 presents 9 specimens of randomly generated joint profiles with different values of D₃ and D₈ by the proposed IDFT method.

5.2 Fourier shape descriptors versus waviness and unevenness

In order to investigate the relationship between the proposed Fourier shape parameters (D₃ and D₈) versus the traditional roughness shape parameters (waviness and unevenness), thirty groups of joint specimens have been reconstructed and analyzed. Each group involved 1000 joint profiles at the same length of 100 mm. The ranges of the Fourier descriptors employed to reconstruct each group of the joint specimen include all the combinations between the following ranges:

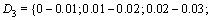
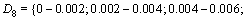
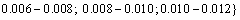
The descriptors D₁ and D₂ are set to 0; D₄ to D₇ and the ones after D₈ are obtained using Eqs. (7) and (8), respectively. For each group, the mean values of roughness shape parameters of waviness and unevenness are computed. The results are presented in Figures 12 and 13. The influences of D₃ (when D₈=0-0.002) and D₈ (when D₃=0-0.01) on the waviness and unevenness respectively are shown in Figure 12. Due to the randomness of the phase angles adopted for each generated joint, one single pair of D₃ and D₈ values might lead to a certain range of waviness and unevenness results (shown as scatter points in Figure 12). The mean values and standard deviations (regarded as upper bound and lower bound) of the obtained waviness and unevenness data for each D₃ and D₈ are plotted in solid line and dot lines respectively. As indicated in Figure 12(a), the descriptor D₃ alone has a marked influence on the waviness shape characteristic. Larger D₃ tends to increase the overall degree of waviness since both the mean value line and the standard deviation lines indicate the positive correlation between D₃ and waviness. It is shown in Figure 12(b) that D₈ alone also has similar impact on the unevenness. The higher value of D₈ will lead to a strong increment of unevenness. Both the mean value line and the standard deviation lines of unevenness have significant upward trends when D₈ varies from 0 to 0.012.

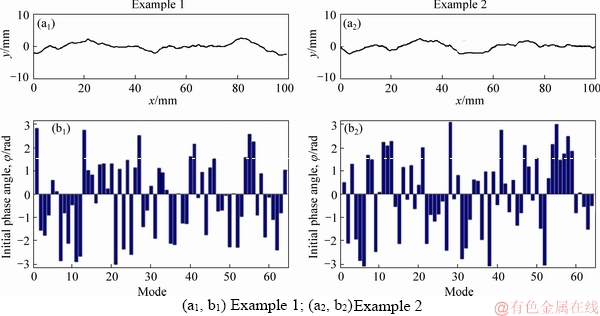
Figure 10 Two examples of reconstructed joint profiles with random values of phase angles:

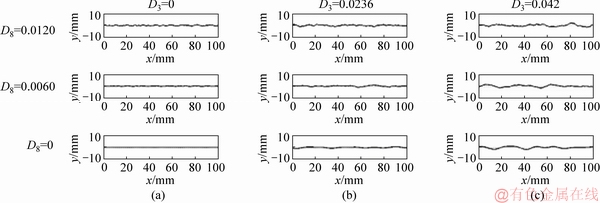
Figure 11 Randomly generated joint profiles at various D₃ and D₈

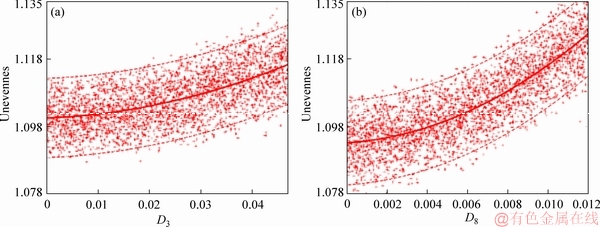
Figure 12 Influence of D₃ on waviness (a) and D₈ on unevenness of reconstructed joints (b) (Solid lines: mean values; Dotted lines: mean values; +/-: standard deviation)

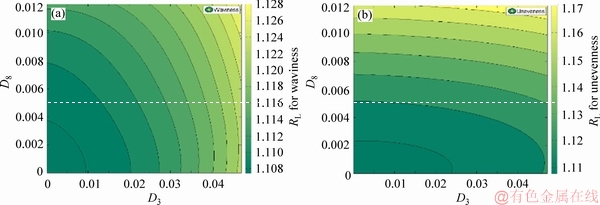
Figure 13 Mean values of waviness (a) and unevenness (b) of joint profile in relation with Fourier descriptors D₃ and D₈

In order to further investigate the indecency of waviness and unevenness on the adopted Fourier descriptors, the mean value of the waviness and unevenness of the generated joint profiles are plotted versus both D₃ and D₈ in Figure 13. As expected, seen from Figure 13, the average waviness is largely influenced by D₃ only while D₈ has minor effect on the waviness shape. The unevenness of the joint shape appears to be strongly dependent on D₈ and rather independent on D₃, which is somehow expected since the unevenness is mostly concerned with the small irregularities of the outline rather than with the larger scale joint shape. Figure 13 could also serve as a reference to estimate waviness and unevenness expected for a joint specimen reconstructed by the proposed method. It could also be employed to choose the descriptors D₃ and D₈ prior to joint reconstruction to match the target shape values of waviness and unevenness. Since the relationships between D₃ and D₈ with the waviness and unevenness have certain deviations, the inverse Monte-Carlo method will be used in the future works to enhance the accuracy of the reconstruction results.

6 Conclusions

1) The 3D laser scanning method has been employed to obtain the realistic joint profile data. Both the traditional digital filtering method and proposed discrete Fourier transform method for shape quantification of joint waviness and unevenness are presented.

2) The evolutions of Fourier amplitudes and phase angles towards the increasing number of harmonic frequencies were studied. It is revealed that amplitudes D_n decrease significantly with the increasing harmonic frequency value n while the phase angles have poor relationship with n. The statistical characteristics of the Fourier amplitudes are also investigated based on statistical analysis of the acquired joint data. It is found that the Fourier amplitudes are well-fitted by the Beta distribution.

3) It is found that the Fourier amplitudes D_n (n≥3) are potentially correlated with the waviness and unevenness shape irregularities. The linear relations in log scale coordinates between the Fourier amplitudes D_n (n≥3) with the harmonic frequency are found to be fitted by the following equations:

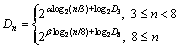
4) The inverse discrete Fourier transform method is employed to reconstruct the joint specimen with prescribed value of Fourier shape descriptor D₃ and D₈. Numerous joint profiles have been reconstructed by the proposed method to study the quantitative relationship between the traditional waviness and unevenness parameters with the propose Fourier descriptor D₃ and D₈. It is revealed that D₃ can be employed to control the shape of waviness while D₈ can be utilized to modify the degree of unevenness for the reconstructed joint profiles. It is expected that the methodology and numerical tools developed in this paper may indeed open a wide range of interesting areas for realistic numerical modeling of rock joint for both academic researches and industrial applications.

References

[1] KWAFNIEWSKI M A, WANG J A. Surface roughness evolution and mechanical behavior of rock joints under shear [J]. International Journal of Rock Mechanics & Mining Sciences, 1997, 34(3, 4): 157-170. DOI: 10.1016/s1365- 1609(97)00042-7.

[2] GRASSELLI G, WIRTH J, EGGER P. Quantitative three-dimensional description of a rough surface and parameter evolution with shearing [J]. International Journal of Rock Mechanics & Mining Sciences, 2002, 39(6): 789-800. DOI: 10.1016/S1365-1609(02)00070-9.

[3] CAO Ping, HE Yun, FAN Xiang, JIANG Zhe. Evolution of morphology texture characteristics based on rock joints shear tests [J]. Journal of Central South University: Science and Technology, 2013, 44(11): 4624-4630. (in Chinese)

[4] LI Y, ZHANG Y. Quantitative estimation of joint roughness coefficient using statistical parameters [J]. International Journal of Rock Mechanics & Mining Sciences, 2015, 77: 27-35. DOI: 10.1016/j.ijrmms.2015.03.016.

[5] YANG Z Y, CHIANG D Y. An experimental study on the progressive shear behavior of rock joints with tooth-shaped asperities [J]. International Journal of Rock Mechanics & Mining Sciences, 2000, 37(8): 1247-1259. DOI: 10.1016/ s1365-1609(00)00055-1.

[6] JIANG Y, LI B, TANABASHI Y. Estimating the relation between surface roughness and mechanical properties of rock joints [J]. International Journal of Rock Mechanics & Mining Sciences, 2006, 43(6): 837-846. DOI: 10.1016/j.ijrmms.2005.11.013.

[7] FARDIN N. Influence of structural non-stationarity of surface roughness on morphological characterization and mechanical deformation of rock joints [J]. Rock Mechanics & Rock Engineering, 2008, 41(2): 267-297.

[8] KWON T H, HONG E S, CHO G C. Shear behavior of rectangular-shaped asperities in rock joints [J]. KSCE J Civ Eng, 2010, 14(3): 323-332. DOI: 10.1007/s00603-007- 0144-9.

[9] LI Y, OH J, MITRA R, HEBBLEWHITE B. A constitutive model for a laboratory rock joint with multi-scale asperity degradation [J]. Computers & Geotechnics, 2016, 72: 143-51. DOI: 10.1016/j.compgeo.2015.10.008.

[10] BARTON N, CHOUBEY V. The shear strength of rock joints in theory and practice [J]. Rock mechanics, 1977, 10(1, 2): 1-54. DOI: 10.1007/BF01261801.

[11] TSE R, CRUDEN D M. Estimating joint roughness coefficients [J]. International Journal of Rock Mechanics & Mining Sciences & Geomechanics Abstracts, 1979, 16(5): 303-307. DOI: 10.1016/0148-9062(79)90241-9.

[12] YU X, VAYSSADE B. Joint profiles and their roughness parameters [J]. International Journal of Rock Mechanics & Mining Sciences & Geomechanics Abstracts, 1991, 28(4): 333-6. DOI: 10.1016/0148-9062(91)90598-G.

[13] GAO Y, WONG L N Y. A modified correlation between roughness parameter Z² and the JRC [J]. Rock Mechanics & Rock Engineering, 2015, 48(1): 387-396. DOI: 10.1007/s00603-013-0505-5.

[14] TATONE B S A, GRASSELLI G. A new 2D discontinuity roughness parameter and its correlation with JRC [J]. International Journal of Rock Mechanics & Mining Sciences, 2010, 47(8): 1391-400. DOI: 10.1016/j.ijrmms.2010.06.006.

[15] CHEN S J, ZHU W C, YU Q L, LIU X G. Characterization of anisotropy of joint surface roughness and aperture by variogram approach based on digital image processing technique [J]. Rock Mechanics & Rock Engineering, 2016, 49(3): 855-876. DOI: 10.1007/s00603-015-0795-x.

[16] SANEI M, FARAMARZI L, GOLI S, FAHZMIFAR A, RAHMATI A, MEHINRAD A. Development of a new equation for joint roughness coefficient (JRC) with fractal dimension: A case study of Bakhtiary Dam site in Iran [J]. Arabian Journal of Geosciences, 2015, 8(1): 465-475. DOI: 10.1007/s12517-013-1147-3.

[17] BROWN, ED E T. Rock characterization, testing & monitoring : ISRM suggested methods [M]. Pergamon Press, 1981. https://www.springer.com/us/book/9783319077123.

[18] BANDIS S, LUMSDEN A C, BARTON N R. Experimental studies of scale effects on the shear behaviour of rock joints [J]. International Journal of Rock Mechanics & Mining Sciences & Geomechanics Abstracts, 1981, 18(1): 1-21. DOI: 10.1016/0148-9062(81)90262-X.

[19] HONG E S, KWON T H, SONG K I, CHO G C. Observation of the degradation characteristics and scale of unevenness on three-dimensional artificial rock joint surfaces subjected to shear [J]. Rock Mechanics & Rock Engineering, 2016, 49(1): 3-17. DOI: 10.1007/s00603-015-0725-y.

[20] HENCHER S R, RICHARDS L R. Assessing the shear strength of rock discontinuities at laboratory and field scales [J]. Rock Mechanics & Rock Engineering, 2015, 48(3): 883-905. DOI: 10.1007/s00603-014-0633-6.

[21] OH J, CORDING E J, MOON T. A joint shear model incorporating small-scale and large-scale irregularities [J]. International Journal of Rock Mechanics & Mining Sciences, 2015, 76: 78-87.

[22] HONG E S, LEE I M, CHO G C, LEE S W. New approach to quantifying rock joint roughness based on roughness mobilization characteristics [J]. KSCE J Civ Eng, 2014, 18(4): 984-991. DOI: 10.1016/j.ijrmms.2015.02.011.

[23] ZHAO Y, WAN W, WANG W, PENG Q Y. Shear numerical simulation of random morphology rock joint and nonlinear shear dilatancy model [J]. Chinese Journal of Rock Mechanics & Engineering, 2013, 32(8): 1666-1676. http://en.cnki.com.cn/Article_en/CJFDTOTAL-YSLX201308021.htm.

[24] YANG L L, XU W Y, MENG Q X, WANG R B. Investigation on jointed rock strength based on fractal theory [J]. Journal of Central South University, 2017, 24(7): 1619-1626. DOI: 10.1007/s11771-017-3567-9.

[25] LI K H, CAO P, ZHANG K, ZHONG K F. Macro and meso characteristics evolution on shear behavior of rock joints [J]. Journal of Central South University, 2015, 22(8): 3087-3096. DOI: 10.1007/s11771-015-2845-7.

[26] ZHAO L H, ZHANG S H, HUANG D L, ZUO S, LI D J. Quantitative characterization of joint roughness based on semivariogram parameters [J]. Int J Rock Mech Min Sci, 2018, 109: 1-8. DOI: https://doi.org/10.1016/j.ijrmms.2018. 06.008.

[27] GREEN R. The spectrum of a set of measurements along a profile [J]. Engineering Geology, 1967, 2(3): 163-168. DOI: 10.1016/0013-7952(67)90015-4.

[28] CHAE B G, ICHIKAWA Y, JEONG G C, SEO Y S, KIM B C. Roughness measurement of rock discontinuities using a confocal laser scanning microscope and the Fourier spectral analysis [J]. Engineering Geology, 2004, 72(3, 4): 181-199. DOI: 10.1016/j.enggeo.2003.08.002.

[29] MOLLON G, ZHAO J. Fourier–Voronoi-based generation of realistic samples for discrete modelling of granular materials [J]. Granular Matter, 2012, 14(5): 621-638. DOI: 10.1007/ s10035-012-0356-x.

[30] ZHAO L, HUANG D, DAN H C, ZHANG S H, LI D J. Reconstruction of granular railway ballast based on inverse discrete Fourier transform method [J]. Granular Matter, 2017, 19(4): 74. DOI: 10.1007/s10035-017-0761-2.

[31] ZHAO L, HUANG S, ZHANG R, ZUO S. Stability analysis of irregular cavities using upper bound finite element limit analysis method [J]. Computers and Geotechnics, 2018, 103: 1-12. DOI: 10.1016/j.compgeo. 2018.06.018.

[32] MELOY T P. Fast fourier transforms applied to shape analysis of particle silhouettes to obtain morphological data [J]. Powder Technol, 1977, 17(1): 27-35. DOI: 10.1016/ 0032-5910(77)85040-7

[33] BOWMAN E T. Particle shape characterisation using Fourier descriptor analysis [J]. Géotechnique, 2001, 51(6): 545-554. DOI: 10.1680/geot.2001.51.6.545.

(Edited by YANG Hua)

中文导读

考虑真实凹凸度与粗糙度特征的岩石节理轮廓傅里叶形态重构方法

摘要：岩石节理形态特征，包括凹凸度与粗糙度，是影响岩石节理剪切行为的重要因素。本研究提出了一种新的岩石节理重构方法，该方法能够考虑与真实节理形态相符的凹凸度与粗糙度特征。首先，采用3D镭射激光扫描的方法获取节理的表面轮廓信息。然后，采用传统的凹凸度与粗糙度指标对节理进行形态特征评价。接着，采用傅里叶变换对节理轮廓进行分析，提出了D₃与D₈两个傅里叶形状指标来分别表征节理的凹凸度与粗糙度。随后，采用傅里叶逆变换，通过设置随机的相位角与调控傅里叶形状指标D₃和D₈的大小来重构节理轮廓。最后，通过采用传统的凹凸度与粗糙度指标对采用傅里叶方法随机重构的节理轮廓进行分析，研究了傅里叶形状指标D₃和D₈与传统的凹凸度和粗糙度指标之间的相关性。结果表明随着D₃的增大，凹凸度增大；随着D₈的增大，粗糙度增大。本文将D₃与D₈和凹凸度与粗糙度之间的相关关系以云图的形式表示出来，为进一步采用随机轮廓重构方法进行岩石节理数值仿真与力学模拟的相关研究提供了依据。

关键词：岩石节理轮廓；节理形态分析；离散傅里叶变换；节理形态重构

Foundation item: Projects(51478477, 51878668) supported by the National Natural Science Foundation of China; Projects(2014122006, 2017-123-033) supported by the Guizhou Provincial Department of Transportation Foundation, China; Project(201722ts200) supported by the Fundamental Research Funds for the Central Universities, China

Received date: 2018-03-10; Accepted date: 2019-03-17

Corresponding author: ZHAO Lian-heng, PhD, Professor; Tel: +86-13755139425; E-mail: zhaolianheng@csu.edu.cn; ORCID: 0000- 0002-8406-5973