文章编号：1004-0609(2014)01-0075-07

线性增加冲击荷载作用下圆盘试样的动态应力平衡

张  盛¹，李新文^{1, 2}，杨向浩¹

(1. 河南理工大学 能源科学与工程学院，焦作 454003；

2. 潞安集团余吾煤业公司，长治 046103)

摘  要：为了考察含有预制裂缝的圆盘试样在SHPB系统上受线性增加冲击荷载作用过程中的应力平衡性，采用ANASYS有限元软件对圆盘试样的动态冲击进行数值模拟，获得圆盘的动态应力时间历程，对圆盘试样两个加载平台及加载直径韧带上节点的应力进行定量对比分析，提出确定动态应力平衡性判定的方法。结果表明：圆盘靠近入射端接触平台面上点的应力一致，而靠近透射端接触平台不同点的应力差异却非常大，尽管裂纹尖端附近节点的拉应力值较为接近，但在冲击载荷作用过程中，圆盘加载直径韧带上对称部分的节点动态应力始终无法达到平衡，较小的应力差异就能引起应力平衡度量值较为严重的振荡。这有助于正确认识岩石动态冲击破坏过程和提出准确测试岩石动态断裂韧度的方法。

关键词：分离霍普金森压杆；应力平衡；圆盘试样；加载直径；动态断裂韧度

中图分类号：O346；TU438　　     文献标志码：A

Dynamic stress equilibrium of disc specimen under linear increase impact loading

ZHANG Sheng¹, LI Xin-wen^{1, 2}, YANG Xiang-hao¹

(1. College of Energy Science and Engineering, Henan Polytechnic University, Jiaozuo 454003, China;

2. Yuwu Coal Industry Corporation, Lu’an Group, Changzhi 046103, China)

Abstract: In order to analyze the stress balance of the prefabricated crack disc specimen impacted under linear increase impact loads in split Hopkinson pressure bar (SHPB) impact system, the dynamic numerical simulation were performed by ANASYS finite element software. The whole dynamic stress history of the disc specimen was got, and the node dynamic stress of two loading platforms and the loading diameter ligament of the disc specimen were compared and analyzed quantitatively. The method to determine dynamic stress equilibrium was introduced, too. The results show that the nodes stress of the platform surface near the incidence end are consistent, while the one near the transmission end are obviously different. Although the node stress near crack tip is relatively close, the dynamic stress of the disc loading diameter ligament on symmetry part are always unable to keep balance, and smaller difference can cause serious stress oscillation. It is helpful to understand the rock dynamic failure and propose a correct test method to determine the dynamic fracture toughness.

Key words: split Hopkinson pressure bar; stress equilibrium；disc specimen；loading diameter；dynamic fracture toughness

在岩土工程中，岩体发生失稳和破坏大多是在动态加载条件下发生的^[1-2]，在深部开采的硬岩的力学特征则可能属于动静组合的更加复杂的作用模式^[3-4]。目前，国内外学者已经应用SHPB装置开展了大量岩石材料动态力学参数测定和动态本构特征的研究工作^[4-11]。在获取岩石的动态抗压强度这样一个宏观材料参数时，多数研究者认为，当采用的一维圆柱体试样达到动态应力平衡时，可忽略试样内部质点由于加速度产生的惯性效应，采用准静态公式即可确定岩石材料参数，应力平衡时间近似等于应力波在试样中往返两次的时间^[5-6]。YANG等^[7]从压杆与试样横截面、波阻抗和上升沿时间等方面对应力平衡的影响进行了分析。毛勇建等^[8]基于一维弹性应力波理论，计算了任意形状的入射波在试样内的应力分布规律，并分析了波形对应力平衡时间的影响，应力平衡性受到试验加载条件以及试样性质等的影响。

当采用圆盘试样测试岩石的动态断裂韧度时，与一维圆柱体试样不同，含有裂缝的圆盘试样是形状复杂的二维、甚至三维试样，即使在静态加载条件下裂纹前缘各点的应力强度因子并不相等^[12]。其次，圆盘较小面积的加载端和预制裂缝对应力波的干扰将会对应力平衡性造成影响。目前，国内外还缺乏对圆盘试样的应力平衡性的深入分析。RODRIGUEZ等^[9]利用LS-DYNA软件对巴西圆盘试样动态冲击过程进行模拟，得到了与光弹实验吻合度高的圆盘应力分布，从而证明了动态有限元分析的可行性，为考察应力平衡提供了思路和方法。李伟^[10]针对平台圆盘试样，采用数值模拟得到了圆盘试样不同时刻的内部动态应力分布情况，但没有采用定量方法进行深入研究，且分析对象是不含预制裂缝的普通圆盘试样。应力平衡性假定如果成立，将有助于简化岩石动态断裂韧度的测试方法，反之，将给实验结果带来较大误差。应力平衡性假定的分析对于获取试样实际受载、研究材料动态本构和应力波传播特性有重要意义。

本文作者利用ANSYS有限元软件，对线性冲击载荷作用下含预制裂缝圆盘试样在SHPB系统动态加载过程进行了动态数值模拟，得到了含有预制裂缝圆盘试样的动态应力时间历程，建立衡量圆盘试样应力平衡程度的度量值公式，对圆盘试样的应力平衡问题进行分析和讨论。

1  圆盘试样动态冲击数值模拟分析

1.1  动态试验加载系统

SHPB动态加载系统如图1所示，采用初速度为v₀的炮弹，径向冲击弹性压杆，应力波由入射杆传到圆盘试样加载平台端面，然后透射过试样传到透射杆上，持续增加的应力加载脉冲作用圆盘端面导致试样预制裂缝尖端发生起裂并扩展。通过距离入射杆L₁和距离透射压杆L₂在压杆上粘贴的应变片监测压杆应变信号，间接计算出圆盘加载两端作用的动态载荷，由有限元模拟分析和裂尖的起裂时间可以确定岩石的动态断裂韧度。这种测试方法被称为实验—数值方法。

图1中，圆盘试样选用中心圆孔裂缝平台巴西圆盘试样(Holed-cracked flattened Brazilian disc，HCFBD)，其预制裂缝方向与弹性压杆加载载荷的夹角为0°。选取岩石材料参数泊松比为0.3，弹性模量为16.3 GPa，密度为2 730 kg/m³。本文作者研究试样几何参数均为圆盘直径80 mm，厚度32 mm，预制裂缝长度40 mm，平台加载角度20°和中心孔直径16 mm的HCFBD试样。

1.2  数值模型的建立

由于HCFBD试样的特殊构型和动态冲击载荷的复杂性，很难利用解析法对试样的应力分布进行分析，采用有限元模拟的方法可以简化这一问题。ANSYS软件拥有强大的前处理功能，多种单元和不同网格划分可以实现建立整体模型的同时对局部细化，能很方便建立含预制裂缝的HCFBD试样。图2所示为采用ANSYS有限元软件建立的试样加载模型。由于试样的对称性，取试样的一半模型对问题进行分析。考虑到使用带中间节点的单元会导致模拟波的传播过程中的质量分配不均匀，采用Plane42平面单元类型。而在在裂纹尖端局部范围内约定的四边形网格会退化为三角形单元构造1/4奇异单元来描述裂缝尖端的应力、应变奇异性。模型施加边界条件为沿预制裂缝方向韧带上施加X方向的位移约束，Y方向自由；试样右端面约束Y方向位移，X方向无约束；左端面施加线性增加脉冲荷载。

考虑到试验波形的差异带来的影响，为了更利于问题的分析，参照文献[11]试验加载载荷峰值与时间历程(试样的破坏发生在200 MPa载荷之前，破坏时间小于200 μs)，选用简化的线性增加的荷载进行分析，如图3所示，在模型左端面施加简化的脉冲荷载，即入射端节点的轴向应力为时间历程为0~200 μs，荷载强度为0~200 MPa的线性增加的脉冲荷载。

图1  圆盘试样在SHPB装置的加载示意图

Fig. 1  Schematic diagram of disc specimen loaded in SHPB system

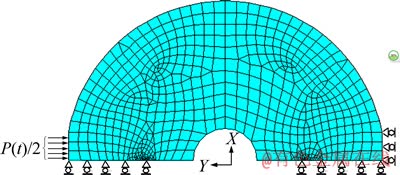
图2  圆盘有限元模型(一半)

Fig. 2  Finite element model of disc sample (half)

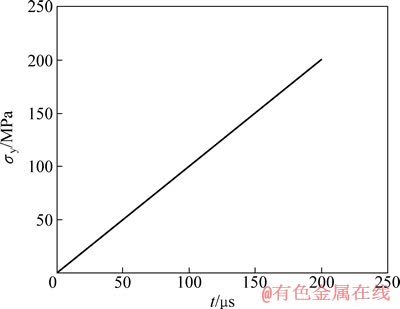
图3  线性增加脉冲载荷

Fig. 3  Linear increasing pulse load

2  有限元模拟结果分析

2.1  动态应力分布云图

不同时刻HCFBD试样垂直裂纹面的动态应力分布云图如图4(a)~(o)所示，其中图4(p)所示为静态应力分布云图。

由图4可以看出，在0~30 μs时段，圆盘试样处于加载初期，入射脉冲通过试样端部逐渐开始对试样进行加载。由于入射脉冲的前半段还没有传播至HCFBD试样的约束端，此时的SHPB装置的加载试样的两端应力差异较大。在30~60 μs时段，压缩弹性波的端头部分已经从加载端逐渐传播到约束端，并在试样与透射杆的接触面上发生反射。同时，在应力脉冲传播的过程中，入射波遇到试样的预制裂缝和内部裂纹均发生散射。由于试样相对较小，入射波端头跟透射杆接触面反射得到的反射波和试样持续不断的入射波又重叠在一起，由应力分布模式可以看出圆盘试样整体仍未达到应力平衡。在60~110 μs时段，对比两端的应力分布云图发现，除了加载两端附近受端部效应的影响，其应力分布模式略微不同，试样内部试样的应力分布模式相对于加载直径的中心线逐渐呈对称分布，似乎达到“应力平衡”。在110~190 μs时段，随着加载时间增加，圆盘加载两端对称部分的应力数值，在不断发生非常接近的对称变化。这种规律与文献[10]对圆盘试样的模拟结果非常吻合，似乎是圆盘试样一旦达到“应力平衡”，将会达到类似于图4(p)静态情况下的应力平衡，不同之处在于应力波的来回反射不断改变试样内的应力值，而应力分布模式会一直保持平衡直至试样发生破坏。然而，单从应力分布图来简单地定义圆盘已经达到应力平衡不进行定量分析，缺少说服力。因此，很有必要对圆盘试样不同位置点的动态应力进行定量分析，来得到更可靠的结果。

2.2  动态应力平衡性的确定方法

根据一维假设条件，假定某一时刻圆柱体试样两端的受力达到了平衡，即可认为圆柱体试样的应力分布达到了动态应力平衡^[13-14]。HCFBD试样属于二维试样，通过比较对称部分节点应力时间历程的差异，由不同时刻的应力值能够确定动态加载过程中的应力平衡程度。HCFBD试样应力平衡指标α_k由式(1)求得，将圆盘试样按照加载方向依据靠近入射端和透射端分为两个部分，定义在t时刻，靠近入射端(Incident side)圆盘试样点的应力σ_I和靠近透射端(Transmission side)圆盘试样点的对称应力σ_T的应力之差与两者的平均值之比为应力平衡度量值α_k。

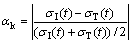                       (1)

式中：当α_k≤5%时，认为试样达到应力平衡。

2.2.1  不同时刻加载平台上的应力对比

考虑到HCFBD试样的对称性，取圆盘两个加载端面上对应节点应力值计算接触面应力平衡程度。平台端部选取的节点如图5所示，定义圆盘中心点为坐标零点，提取圆盘加载平台沿Y方向上节点的应力。圆盘加载端节点位置用X表示，当X=0时，表示圆盘加载直径方向与圆盘试样平台相交的节点；X为1/4、1/2、3/4分别表示圆盘一半加载平台上分别位于其1/4、1/2和3/4处的节点；X=1表示圆盘平台边缘与弧形自由面的交点。同时采用下标表示不同的两个加载端面，X_I和X_T分别表示圆盘靠近入射端和透射端上的节点。

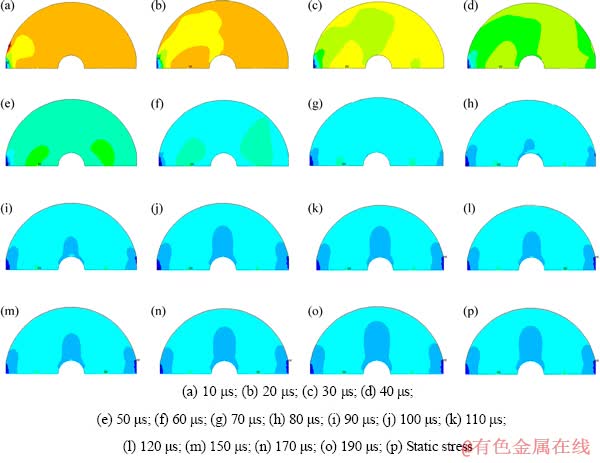
图4  HCFBD试样加载过程中不同时刻的应力分布云图

Fig. 4  Stress distribution nephogram of HCFBD during dynamic loading at different times

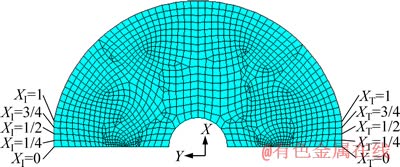
图5  圆盘加载端平台选取的节点

Fig. 5  Nodes selected from loading platform of disc

圆盘加载平台上点的动态应力曲线如图6所示，由于靠近圆盘入射端平台面上节点应力与加载脉冲一致，采用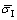表示；靠近圆盘透射端平台面上节点的应力差异较大，采用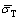表示，由靠近透射端平台面的应力加权平均值获得。由图6可以看出，圆盘入射端平台面加载应力与线性增加脉冲一致，但是透射端加载端不同节点的应力随加载时间却并非线性增加，且不同节点应力具有明显的差异。透射杆对HCFBD圆盘试样位移约束对其端面应力分布有较大的影响。另外，在靠近透射端加载平台上节点的应力越靠近平台面与圆盘弧形面相交点(X=1)的应力越大，平台面中间位置节点应力值最低。靠近入射端和透射端的两个平台面上的应力平均值在加载过程中始终不会相等。

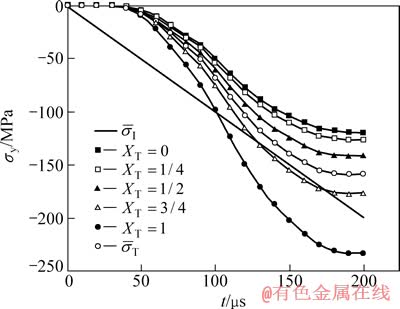
图6  圆盘加载平台上点的动态应力曲线

Fig. 6  Dynamic stress curves of nodes in loading platform of disc

利用式(1)对图3所示圆盘两平台上对应节点确定的平衡度量值α_k如图7所示。由图7可以看出，两个加载平台位于X_I=3/4和X_T=3/4位置的点，在121~187 μs时刻，其平衡度量值α_k＜5%；但之后，α_k值又开始增加；平台边缘部位节点(X=1)在t=97 μs首次达到5%后，经过约8 μs之后，其应力平衡度量值α_k>5%。两加载平台端平均应力的α_k始终大于5%。在动态加载峰值之前(加载时间200 μs)，所有平台上的点并不能保证在应力平衡。

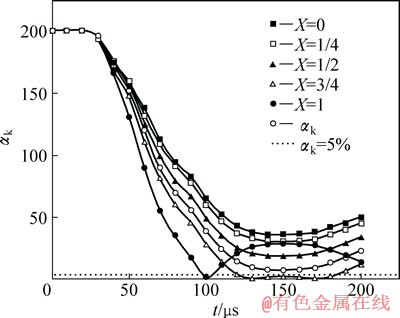
图7  圆盘两加载平台应力平衡度量值

Fig. 7  Stress balance values calculated by nodes stress in two loading platforms of disc

2.2.2  加载直径韧带上点的应力平衡分析

为了对圆盘试样的应力平衡性问题进行深入分析，仅仅利用端部加载平台的轴向应力对应力平衡性探讨是不够的，需要选取HCFBD试样内部的代表性节点。在动态加载时，HCFBD试样首先在预制裂纹尖端受到拉应力起裂破坏，并沿加载直径扩展直至失效^[11]。因此，有必要选取过预制裂纹尖端的加载直径韧带上点的应力进行对比，加载直径韧带的点是指在圆盘上与圆盘试样的加载方向一致的直径上韧带上的点，本研究中，仅考虑二维情况。

为了比较在不同时刻加载直径上对应节点应力的相对变化，取HCFBD试样沿加载直径方向的两端到圆盘中心点的距离l，对比靠近圆盘入射端和透射端 对称位置上节点的应力。图8所示为HCFBD试样在不同时刻左右两端沿加载直径上点的X方向的应力分布图。在图8中，Y_I表示圆盘加载直径韧带上靠近圆盘入射端(Incident side)的节点，Y_T表示圆盘加载直径韧带上靠近圆盘透射端(Transmission side)的节点。从图8可以看出，圆盘加载直径韧带上节点的应力差异较大，大部分范围的应力为拉应力，靠近裂缝尖端附近的拉应力远大于试样其它位置上节点的应力；但靠近加载端部范围点的应力为压应力，整个加载直径上，拉应力范围大于压应力范围。在动态加载初期，圆盘加载直径韧带上节点的应力差异较小，但是随着加载时间的增加，节点应力的差异明显增强。另外，在同一加载时刻，靠近入射端加载直径上节点的应力和靠近透射端加载直径上节点的应力之间的差异始终存在，尤其在两个加载端部的应力差异比裂缝尖端附近的应力差异更为严重。

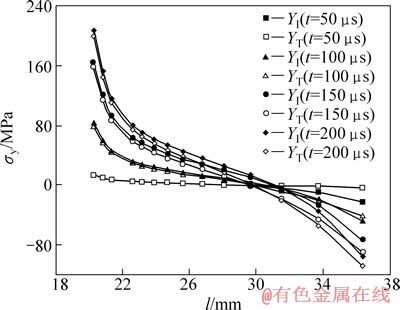
图8  圆盘加载直径上节点的动态应力曲线

Fig. 8  Node stress curves of along loading diameter of disc

图9所示为根据式(1)计算得到的圆盘遭受冲击过程中，在t为50、100、150和200 μs时刻，沿加载直径韧带上对应节点的应力平衡度量值α_k。对比不同时刻的度量值发现，随着加载时间的增加，加载直径上节点的应力平衡度量值均有减小的趋势，当两个裂纹尖端附近点的应力平衡度值α_k≤5%，可以认为达到了应力平衡。但是试样加载直径上26~34 mm的范围内，其应力平衡度量值振荡较为严重，其节点的度量值最高达160%；而且随着加载时间的增加，应力平衡程度并未得到改善。加载直径上节点应力在拉应力和压应力较小的范围内，相对于裂纹尖端较小的应力差异可能引起较大的应力平衡度量值的起伏，试样加载直径上对称部分节点的应力始终无法达到应力平衡。

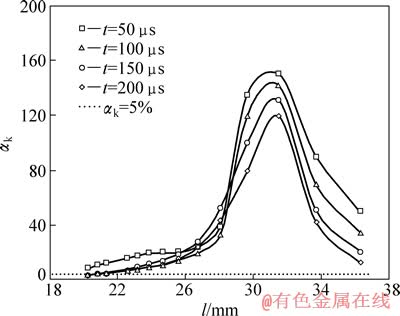
图9  圆盘加载直径上节点的应力平衡度量值

Fig. 9  Stress balance values of node along loading diameter of disc

2.2.3  圆盘试样应力不平衡的原因分析

对于圆柱体试样测试岩石动态抗压强度测试时，圆柱体试样遭受轴向加载，与压杆接触面积大，一维性假定和应力均匀假定相对容易满足。但对于有缺陷、预制裂缝的构型相对复杂的HCFBD试样，应力波在预制裂纹表面发生散射，更为复杂的是应力波将在试样与自由面产生反射无旋波、反射等容波、透射无旋波和透射等容波^[15]将使得HCFBD试样很难在较短的上升沿时间内达到应力平衡。带有预制裂缝的圆盘试样并不像一维构型的圆柱体试样，它属于复杂的二维甚至三维构型，其预制裂缝对应力平衡性的干扰不能忽略。

至于试样在动态加载时不容易满足应力平衡假定的原因，徐明利等^[16]也给出了一些解释，他认为当弹性压杆不变，压杆与圆盘试样加载端面积之比越大，试样中应力达到平衡的时间越长。即使对于压杆与试样加载端面积之比等于4时，平衡因子在大约8τ时也达到0.93没有达到应力平衡，其中τ为应力波穿越试样的时间。

对本研究模拟采用的HCFBD试样来说，不考虑预制裂缝的影响，仅仅考虑加载端面影响，圆盘试样与压杆接触的是加载平台面积，压杆与圆盘试样加载端面积之比达17.5，τ值大约为32 μs，远大于4，推算在200 μs时刻内是根本无法达到应力平衡的。而此时根据试验分析，试样早已破坏。利用较大尺寸的圆盘试样能够在一定程度上使得压杆与圆盘试样加载端面积之比变小^[17]，但其τ值也随之增加。在试样破坏之前，要达到应力平衡，非常困难。

2.2.4  应力平衡性对于实验—数值方法确定岩石动态断裂韧度影响的讨论

采用圆柱体岩石试样确定岩石动态抗压强度时，应力平衡性假定是一个必须满足的条件。一方面，岩石动态抗压强度的测试仍然采用静态公式，要求两个加载端受载相等；另一方面，动态抗压强度是一个描述材料宏观抵抗破坏能力的参数，它要求材料受载后必须达到应力平衡，这样测试值得到的动态抗压强度才能反映材料整体宏观上的承载能力。由此可见，基于准静态方法确定材料动态力学参数有着严格的假设条件。

更多试验表明，由于岩石材料是一种准脆性材料，在试样遭受动态冲击作用后，事先预制的裂纹没有足够的时间在达到应力平衡之前发生起裂破坏。与岩石动态抗压强度不同的是，动态断裂韧度是考察裂纹的动态起裂和扩展能力，不是一个考虑材料宏观性能的参数。基于SHPB装置的实验-数值方法，借助于动态数值方法对实验数据的分析，通过对材料动态应力强度因子的时间历程进行分析，已经考虑了惯性效应对材料参数确定的影响，不需要满足准静态方法的假设条件。试验时，只需知道每个裂尖的动态应力强度因子和相对应的起裂时间，就可以确定材料的动态断裂韧度值。因此，应力平衡性假设对于准静态确定方法是一个前提条件，但对于采用实验-数值方法确定岩石动态断裂韧度并不是一个必要条件，尽管应力平衡性对于试样两端载荷的准确确定会造成一定的影响。

3  结论

1) 建立了考察圆盘试样应力平衡度量计算公式，即通过圆盘加载方向对称点应力之差与应力平均值之比计算应力平衡度量值，对试样进行应力平衡性判断。

2) 圆盘试样入射端平台各点动态应力一致，但透射端平台上不同节点的动态应力差异较大，圆盘试样加载直径韧带上节点应力平衡的度量值最高达160%，试样加载直径上对称部分节点的应力始终无法达到应力平衡。

3) 带有裂缝的圆盘试样并不像一维构型的圆柱体试样，属于复杂的二维甚至三维构型，且其预制裂缝对于应力波的干扰以及圆盘加载平台面积与SHPB压杆截面积比值较小，是HCFBD试样在破坏之前无法达到应力平衡的主要原因。

REFERENCES

[1] CRESPELLANI T, MADIAI C, VANNUCHI G. Earthquake destructiveness potential factor and slope stability[J]. Geotechnique, 1998, 48(3): 411-419.

[2] HAVENITH H B, VANINI M, JONGMANS D. Initiation of earthquake-induced slope failure: Influence of topographical and other site specific amplification effects [J]. Journal of Seismology, 2003, 7(3): 397-412.

[3] 李夕兵, 姚金蕊, 宫凤强. 硬岩金属矿山深部开采中的动力学问题[J]. 中国有色金属学报, 2011, 21(10): 2551-2553.

LI Xi-bing, YAO Jin-rui, GONG Feng-qiang. Dynamic problems in deep exploitation of hard rock metal mines[J]. The Chinese Journal of Nonferrous Metals, 2011, 21(10): 2551-2553.

[4] LI X B, ZHOU Z L, LOK T S, HONG L, YIN T B. Innovative testing technique of rock subjected to coupled static and dynamic loads[J]. International Journal of Rock Mechanics and Mining Sciences, 2008, 45(5): 739-748.

[5] 董世明, 汪 洋, 夏源明. 应力脉冲对 CCCD-SHPB试验系统测试结果影响的数值分析[J]. 四川大学学报, 2007, 29(2): 212-216.

DONG Shi-ming, WANG Ming, XIA Yuan-ming. Numerical Analysis of effects of stress impulse on testing result for CCCD-SHPB dynamic fractures test system[J]. Journal of Sichuan University, 2007, 29(2): 212-216.

[6] RAVICHANDRAN G, SUBHASH G. Critical appraisal of limiting strain rates for compression testing of ceramics in a split Hopkinson pressure bar[J]. Journal of the American Ceramic Society, 1994, 77(1): 263-267.

[7] YANG L M, SHIM V P W. An analysis of stress uniformity in split Hopkinson bar test specimens[J]. International Journal of Impact Engineering 2005, 31(2): 129-150.

[8] 毛勇建, 李玉龙. SHPB试验中试件的轴向应力均匀性[J]. 爆炸与冲击, 2008, 28(5): 448-454.

MAO Yong-jian, LI Yu-long. Axial stress uniformity in specimens of SHPB tests[J]. Explosion and Shock Waves, 2008, 28(5): 448-454.

[9] RODRIGUEZ J, NAVARRO C, SANCHEZ-GALVEZ V. Splitting tests: An alternative to determine the dynamic tensile strength of ceramic materials[J]. Journal de Physique IV, 1994, 4(C8): 101-106.

[10] 李 伟. 大理岩动态力学性能的分离式霍普金森杆实验研究[D]. 成都: 四川大学, 2005.

LI Wei. Experimental study for dynamic mechanical properties of marble using split Hopkinson pressure bar[D]. Chengdu: Sichuan University, 2005.

[11] 张 盛, 王启智. 采用中心圆孔裂缝平台圆盘确定岩石的动态断裂韧度[J]. 岩土工程学报, 2006, 28(6): 723-728.

ZHANG Sheng, WANG Qi-zhi. Method for determination of dynamic fracture toughness of rock using holed-cracked flattened disk specimen[J]. Chinese Journal of Geotechnical Engineering, 2006, 28(6): 723-728.

[12] 张 盛, 梁亚磊. 中心圆孔圆盘试件三维最大无量纲应力强度因子的标定[J]. 中国有色金属学报, 2012, 22(8): 2347-2352.

ZHANG Sheng, LIANG Ya-lei. Calibration of three-dimensional maximum dimensionless stress intensity factor of holed flattened Brazilian disc specimen[J]. The Chinese Journal of Nonferrous Metals, 2012, 22(8): 2347-2352.

[13] GOMEZ J T, SHUKLA A, SHARMA A. Static and dynamic behavior of concrete and granite in tension with damage[J]. Theoretical and Applied Fracture Mechanics, 2001, 36(1): 37-49.

[14] 赵习金, 卢芳云, 林玉亮. 硅橡胶的动态压缩实验和力学性能研究[J]. 高压物理学报, 2004, 18(4): 328-332.

ZHAO Xi-jin, LU Fang-yun, LIN Yu-liang. Research on dynamic compressive testing and mechanical properties of silicon rubber[J].Chinese Journal of High Pressure Physics, 2004, 18(4): 328-332.

[15] 王礼立. 应力波基础[M]. 北京: 国防工业出版社, 2005.

WANG Li-li. Foundation of stress waves [M]. Beijing: National Defense Industry Press, 2005.

[16] 徐明利, 张若棋, 张光莹. SHPB实验中试件内早期应力平衡分析[J]. 爆炸与冲击, 2003, 23(3): 235-240.

XU Ming-li, ZHANG Ruo-qi, ZHANG Guang-ying. Analysis of early stage specimen stress equilibrium in SHPB experiment[J]. Explosion and Shock Waves, 2003, 23(3): 235-240.

[17] WANG Q Z, ZHANG S, XIE H P. Rock dynamic fracture toughness tested with holed-cracked flattened Brazilian discs diametrically impacted by SHPB and its size effect[J]. Experimental Mechanics, 2010, 50(7): 877-885.

(编辑  李艳红)

基金项目：国家自然科学基金资助项目(51004043)；河南理工大学硕士学位论文创新基金资助项目(2011-M-39)

收稿日期：2013-11-28；修订日期：2013-03-07

通信作者：张  盛，副教授，博士；电话：0391-3987934；E-mail：zsroy2002@163.com