RCC-AC路面温度荷载型断裂的有限元分析

 曾四平¹, 郭少华², 陈绍名³ , 付 军⁴

(1.同济大学 交通运输学院,上海,200092;2.中南大学 土木建筑学院, 湖南 长沙, 410083;
3.深圳职业技术学院 建工系, 广东 深圳,518055 ;4.西南电力设计院 勘测处, 四川 成都 ,610021)

摘要: 在沥青水泥混凝土AC层中接缝的上方存在一条垂直路面结构的反射裂缝的条件下,研究温度变化对反射裂缝的影响,并考虑沥青水泥混凝土AC层与碾压水泥混凝土RCC板之间的接触,摒弃两层之间完全连续的假设。其步骤为:利用传热学原理,得出路面结构的温度场,再利用热弹性理论求出不同温度条件下产生的热应力;然后,利用断裂力学理论计算复合式路面裂缝尖端的应力强度因子。此外,根据工程实例得出了不同裂缝长度下的应力强度因子,并分析了不同因素对应力强度因子的影响。研究结果表明:降低AC层与RCC板之间的粘结程度,加铺低模量的土工布,适当提高AC层的厚度等方法,能降低裂缝尖端的应力强度因子,从而达到阻碍反射裂缝开裂扩展的作用。
关键词: 温度荷载; 应力强度因子; 传热学; 反射裂缝
中图分类号:TU318⁺.1 文献标识码:A 文章编号: 1672-7207(2005)01-0149-05

Finite Element Analysis of Temperature Fracture
in RCC-AC Composite Pavement

ZENG Si-ping¹,GUO Shao-hua²,CHEN Shao-ming³,FU Jun⁴

(1.School of Transportation ,Tongji University, Shanghai 200092, China;
2.School of Civil and Architectural Engineering, Central South University, Changsha 410083, China;
3.Department of Civil Engineering, School of Shenzheng Professional Technology, Shenzhen 518055, China;
4.Reconnaissance Department, Southeast Electric Power Design Office, Chengdu 610021, China)

Abstract: On the condition that a reflecting crack existing in AC layer is perpendicular to the pavement and above the jointed crack, the impact of changes of temperature on the crack is studied, and the contact between AC and RCC layers is considered, which gives up the hypothesis that these two layers are complete continuance. The distribution of temperature field of composite pavement is obtained using heat transfer theory, then the thermal stress caused is obtained using thermal elastic theory. At last, the stress intensity factor(SIF) of crack tip in the composite pavement is obtained using fracture mechanics theory. SIFs of different length cracks are obtained in a real engineering instance, and the impacts of different factors on SIF are considered. The results show that abasing the interlayer bond between AC layer and RCC plate, and adding low module geo-textile between them, adding the thickness of AC layer properly and so on, the SIF of crack tip will be decreased, which can prevent the initiation and expanding of reflecting crack effectively.
Key words: thermal load; stress intensity factor; heat transfer theory; reflecting cracking 

碾压水泥混凝土RCC与沥青水泥混凝土AC复合式路面能大大提高路面的使用性能,但其存在反射裂缝,导致其使用寿命低。倪明等通过研究发现^[1-5],除行车荷载外,温度变化是引起反射裂缝开裂扩展的一个重要因素。一些研究者对普通的刚、柔性路面的应力计算进行了大量研究^[6-12],但对温度变化对复合式路面反射裂缝的影响的研究较少。在此,作者就温度变化对反射裂缝的影响进行研究。

1 分析方法与计算模式

目前,人们对公路随温度变化引起的热应力的计算仍采用Westergaard-Bradbury理论,但此理论中的薄板理论假设显然与RCC-AC 复合式路面不符,为此,采用有限元理论进行探讨,并进行如下假设:

a. 路面的自重忽略不计。

b. 各层材料均视为各向同性的线弹性材料。

c. 在任意时刻,路面体内的温度在同一水平面上保持为常量,但随深度变化而变化。

d. 将路面结构的计算问题视为平面应变问题。
1.1 RCC-AC复合式路面结构的温度场

RCC-AC复合式路面结构的力学模型如图1所示,它将路面结构分为4层,即:AC层,RCC板,基层与土基。为了体现层间接触情况对温度应力的影响,在AC层与RCC板之间设置了Goodman夹层。这是一种典型的层状结构,在半刚性基层中有1条垂直路面结构的裂缝,将路面结构按图2所示进行有限元离散,由传热学及层状路面温度场的理论可知^[8,13],RCC-AC复合式路面结构温度场的微分方程为:

式中:Δt为所取的时间步长;{T}_t-Δt为初始温度场列向量;{T}t为时刻的温度场列向量;[K₁]为温度刚度矩阵;[N]为非稳态变温矩阵;{p}t为等式右端项组成的列向量;[K₁],[N]和{p}t的具体表达式见文献[13]。由此可求得时间间隔为Δt时各个时刻的温度场。
1.2 温度变化所引起的等效节点力

由于温度均匀变化,由热弹性理论可知,将在路面体内产生温度翘曲应力,将路面体按上述方式划分网格后,转化为等效节点力^[14,15]:

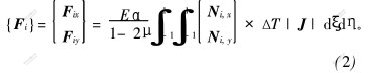
其中:;[J]为雅可比矩阵;N_i,x和N_i,y由四边形八节点单元求得,由此可得荷载列阵{F};i=1,2,…,8;利用平衡方程{F}=[K]{δ},便可求得各结点的位移,然后由{σ}=[D][B]{δ}e-[D]{ξ₀},{ξ₀}=(1+μ)αT[1,1,0]^T可求得各结点的应力。

图 1   路面结构的力学模型
Fig. 1   The mechanics model of pavement

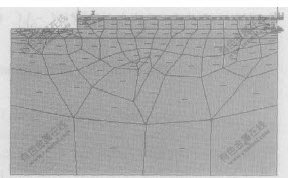
图 2   路面结构的有限元划分
Fig. 2   The finite element model of
pavement structure

1.3 结构单元分析

在用有限元求解时,为了反映层间结合状态和裂尖应力的奇异性,采用以下几种单元。
1.3.1 普通的八节点四边形单元和Goodman 夹层单元

对路面结构各层,均采用八节点四边形单元,这是一种普通单元,为了反映AC层与RCC板的接触情况对反射裂缝的影响,在两板之间增加了夹层单元,其单元结构如图3所示,其单元结构矩阵参见文献[11], 而其他层之间的接触情况仍假设为连续。
1.3.2 裂尖应力奇异单元

由断裂力学理论可知,裂缝尖端应力具有奇异性,普通单元不能很好地反映这种奇异性,为此需要进行特殊处理, 这时只需将裂尖周围等单元边中结点移至裂缝尖端1/4分点处,就可使裂尖角点的应力具有r^-1/2的奇异性,如图4所示。 上述单元虽然形式各异,各自的单元刚度矩阵不同,但组合成总刚度矩阵的原则是一样的。

图 3   Goodman夹层单元
Fig. 3   Goodman interlayer element

图 4   裂尖应力奇异单元
Fig. 4   Singular element at crack tip

 1.4 应力强度因子的计算

因为温度荷载所引起的断裂均为I型断裂,所以只需求η_Ⅰ。应力强度因子与应力的关系为:

可见,只要求得裂缝尖端的应力分布,利用外推法就可求得相应的应力强度因子。

2 工程实例与结果分析

有一RCC-AC复合式路面,其结构如图1所示,日气温变化规律近似正弦函数,即

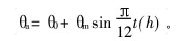
其中θ₀=-5℃, θ_m=10℃,,路面放热系数β=84kJ/(m²·h·℃),其他参数见表1。由有限元法计算,不同时刻不同路面深度处的温度见表2,AC板的板底温度应力见表3,由此可得裂缝尖端的应力强度因子随裂缝长度的变化(如图5所示)。采用有限元法所得翘曲应力与实验值及文献[9]中的计算值比较结果见表4。可见,采用有限元法所得结果与实验结果及文献[9]中的结果相吻合。裂缝的长度[CM(22] 越大,其应力强度因子越大,虽然日温度变化对反

表 1   路面结构的计算参数
Table 1   Computing parameters of pavement structure

表 2   温度梯度最小和最大时的路面温度
Table 2   The pavement temperature at the time of maximum temperature
gradient and the lowest temperature θ/℃     
 
表 3   厚度为4 cm的AC层在不同时间的AC层板底温度应力
Table 3   The thermal stress of the bottom of AC layer at different time
when the thickness of AC layer is 4 centimeters 温度应力/MPa       

表 4   本法与其他方法及实验值之比较
Table 4   Comparison of this method to others
and experimental results

射裂缝的影响尚不足以引起裂缝的开裂(沥青混凝土的断裂韧度通常为0.5~0.8 MPa·m^1/2),但如果考虑疲劳以及行车荷载,它的影响是不可忽略的。改变层间的接触状态,得应力强度因子随界面模量的变化曲线如图6所示。改变AC层的厚度,应力强度因子随AC层厚度的改变如图7所示。可见,随着AC层厚度的增加,应力强度因子减小。裂尖应力强度因子的变化曲线如图8所示。可见,铺设低模量的土工布,有利于抑制温度变化引起的反射裂缝扩展。

图 5   裂尖应力强度因子η随裂缝长度的变化曲线
Fig. 5   The variation curve of stress intensity
factor according to the length

图 6   裂尖应力强度因子η随界面模量λ_s的变化曲线
Fig. 6   The variation curve of stress intensity
factor to different λ_s

 裂缝长L/cm: 1—12; 2—14; 3—16; 4—18
图 7   裂尖应力强度因子η随AC层厚的变化曲线
Fig. 7   The variation curve of stress intensity
factor To the thick of AC

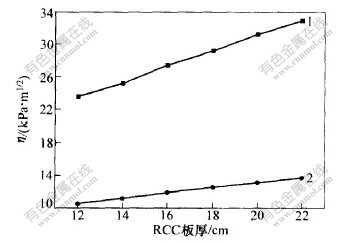
 1—未铺土工布; 2—铺土工布
图 8   加铺土工布层对应力强度因子η的影响
Fig. 8   The influence of geotextile to
the stress intensity factor

3 结 论

a. 复合式路面的应力强度因子随裂缝长度的增加而变大。

b. 界面模量越大,即AC层与 RCC板接触越好,温度应力越大,裂缝尖端的应力强度因子也就越大。

c. 增加AC层的厚度,有助于减少裂尖的应力强度因子,但AC层超过一定厚度后,其对应力强度因子的影响变小,这时单纯靠增大AC 层的厚度来减少应力强度因子,既不经济,也起不到明显的效果。

d. 在全路面段AC层与RCC板之间铺设一层模量较低的土工布应力应变消散夹层,能减小应力强度因子。

参考文献:

[1]倪明,姚祖康.旧水泥混凝土路面上沥青加铺层的应力分析[J].同济大学学报,1989,17(1):33-41.
NI Ming, YAO Zhu-kan. The Stress Analysis of Asphalt Overlay on Deteriorated Concrete Pavement[J]. Journal of Tongji University, 1989,17(1):33-41.
[2]俞建荣,陈荣生.碾压混凝土与沥青混凝土复合式路面中碾压水泥混凝土板的最大温度梯度[J].中国公路学报,1996,9(4):29-37.
YU Jian-rong, CHEN Rong-sheng. The Maximum Temperature Gradient of RCC on the Combined Pavement of RCC and AC[J]. China Journal of Highway and Transport, 1996,9(4):29-37.
[3]邹春伟,郭少华.温度变形对刚性路基的影响[J].中南工业大学学报(自然科学版), 2003,34(2):208-210.
ZOU Chun-wei, GUO Shao-hua. The Influence of Temperature Deformation of Concrete Pavement Roadbed[J]. Journal of Central South University of Technology(Natural Science), 2003,34(2):208-210.
[4]戴时云,胡长顺,王秉刚.碾压混凝土与沥青混凝土复合式路面结构的温度应力分析[J].西安公路交通大学学报,1995,15(2):1-6.
DAI Shi-yun, HU Chang-shun, WANG Bing-gang. The Temperature Stress Analysis Rolled Compacted Concrete and Asphalt Concrete Composite Pavement[J]. Journal of Xi′an Transportation University,1995,15(2):1-6.
[5]俞建荣,陈荣生,金志强.用沥青砼罩面的碾压砼路面板的温度应力分析[J].东南大学学报.1996,26(4):101-105.
YU Jian-rong , CHEN Rong-sheng, JIN Zhi-qiang. Temperature Stress Analysis of Roller Compacted Concrete Pavement with Asphalt Concrete Overlay[J]. Journal Southeast University,1996,26(4):101-105.
[6]李鹏.复合式路面设计与施工工艺的探析[J].中国市政工程,2002,100(2):14-16.
LI Peng. The Analysis of Composite Pavement′s Design and Construction Proceeding[J]. China Municipal Engineering, 2002,100(2):14-16.
[7]周富杰,孙立军.复合路面荷载型反射裂缝的力学分析和试验验证[J].土木工程学报,2002,35(1):50-56.
ZHOU Fu-jie, SUN Li-jun. Behavior of Reflection Cracking in Composite Pavement[J]. Journal of Civil Engineering, 2002,35(1):50-56.
[8]胡长顺,王秉刚.复合式路面设计原理与施工技术[M].北京:人民交通出版社,1999.
HU Chang-shun, WANG Bing-gang. The Design Principals and Construction Technology of Composite Pavement[M].Beijing:The People Transportation Press,1999.
[9]邹春伟,郭少华.带裂缝混凝土路面的极限承载力[J].中南工业大学学报(自然科学版), 2002, 33(5):466-468.
ZOU Chun-wei, GUO Shao-hua. Load-carrying Capacity of a Concrete Pavement with Cracks[J]. Journal of Central South University of Technology(Natural Science), 2002, 33(5): 466-468.
[10]贾玉钧,胡长顺,王秉纲.复合式路面荷载应力的统一分析方法[J].西安公路交通大学学报,1995,15(4):6-13.
JIA Yu-jun, HU Chang-shun, WANG Bing-gang. General Analysis for Load Stress of Composite Pavement[J]. Journal of Xi′an Highway University, 1995,15(4):6-13.
[11]黄晓明,刘玉荣,邓学钧.旧水泥混凝土道面加铺层有限元分析方法[J].中国公路学报,1996,9(1):30-36.
HUANG Xiao-ming,LIU Yu-rong, DENG Xue-jun. Finite Element Analysis of Overlay on Deteriorated Concrete Pavement[J]. Journal of China Highway and Transport, 1996, 9(1):30-36.
[12]孙璐,郑凯.柔性路面中层底面弯拉应力分析[J].重庆交通学院学报,1998,17(4):24-28.
SUN Lu, ZHENG Kai. Analysis on Stresses of Flexible Pavement Surface[J]. Journal of College of Chongqing Transportation, 1998, 17(4):24-28.
[13]孔祥谦.有限单元法在传热学中的应用[M].北京:科学出版社,1998.
KONG Xiang-qian. The Application of Finite Element Method in Transmitting Heat Theory[M]. Beijing: Science Press,1998.
[14]张起森,郑健龙,刘益河.半刚性基层沥青路面的开裂机理[J].土木工程学报,1992,25(2):13-22.
ZHANG Qi-sen,ZHANG Jian-long, LIU Yi-he. Cracking Mechanism for the Semi-rigid Base[J]. Journal of Civil Engineering, 1992, 25(2): 13-22.
[15]郑健龙,张起森.半刚性路面反射裂缝及其应力强度因子的有限元分析[J].岩土工程学报,1990,12(3):22-30.
ZHENG Jian-long, ZHANG Qi-sen. The Finite Element Analysis of Reflecting Crack in Semi-frigid Pavement and Its Stress Intensity Factor[J]. Journal of Rock and Soil Engineering, 1990, 12(3): 22-30.

收稿日期:2004-09-03

基金项目:国家自然科学基金资助项目(50178014)

作者简介:曾四平(1976-),男,湖南衡阳人,博士,从事路面力学和路面结构研究

论文联系人: 曾四平,男,博士;电话:021-65987437;E-mail:zspzspzsp760625@yahoo.com.cn