J. Cent. South Univ. (2012) 19: 424-432
DOI: 10.1007/s11771-012-1021-6
Multiple linear system techniques for 3D finite element method modeling of direct current resistivity
LI Chang-wei(李长伟)1, 2, XIONG Bin(熊彬)2, QIANG Jian-ke(强建科)1, L? Yu-zeng(吕玉增)2
1. School of Geoscience and Info-physics, Central South University, Changsha 410083, China;
2. College of Earth Sciences, Guilin University of Technology, Guilin 541004, China
? Central South University Press and Springer-Verlag Berlin Heidelberg 2012
Abstract: The strategies that minimize the overall solution time of multiple linear systems in 3D finite element method (FEM) modeling of direct current (DC) resistivity were discussed. A global stiff matrix is assembled and stored in two parts separately. One part is associated with the volume integral and the other is associated with the subsurface boundary integral. The equivalent multiple linear systems with closer right-hand sides than the original systems were constructed. A recycling Krylov subspace technique was employed to solve the multiple linear systems. The solution of the seed system was used as an initial guess for the subsequent systems. The results of two numerical experiments show that the improved algorithm reduces the iterations and CPU time by almost 50%, compared with the classical preconditioned conjugate gradient method.
Key words: finite element method modeling; direct current resistivity; multiple linear systems; preconditioned conjugate gradient; recycling Krylov subspace
1 Introduction
Direct current (DC) resistivity methods are widely used in geophysical near-surface investigations. Realistic 3D resistivity inversion remains challenging because of such factors as under-determination and large amounts of data. In particular, finding the solution of the forward problem could be a very time-consuming task, and the forward solver computational efficiency is an important factor of robust inversion. During the past few decades, many efforts have been put into the development of the direct current resistivity forward problem [1-5]. Due to the permission of flexible mesh refinement technique and complicated topography modeling, the finite element method (FEM) is one of the most popular choices for solving 3D resistivity inversion problems.
Finite element method forward problem of DC resistivity is governed by a Possion equation, and experience shows that the mixed boundary condition is a reasonable option on subsurface boundary [1, 6]. The solution of the forward problem using the FEM method involves a large, sparse linear system. Typical 3D resistivity surveys may involve several hundreds electrode positions, and every inversion iteration step needs to solve the forward problem at least s times, where s is the number of different source electrodes employed. With domain discretization, the FEM method results in a sequence of large sparse linear systems with forms similar to the following equation:
Aixi=bi (i=1, 2, …, s) (1)
where the coefficient matrix A represents the discretization conductivity model and is a symmetric positive definite (SPD) matrix, the solution vector x includes the unknown potentials, the right hand vector b characterizes the geoelectrical source, and the index i indicates different source electrode positions. The coefficient matrices in Eq. (1) differ only by low-rank matrices.
A direct solver is one possibility for solving such multiple linear systems [7-8]. However, the main problem with direct solvers is their expensive memory and computational requirements, which make them prohibitive to solving large 3D problems [9]. In this case, iterative methods are the only available choice. Iterative solvers have low storage requirements, and the computational cost per iteration is small. Furthermore, iterative solvers are easier to parallelize than direct solvers, which is important for very large problems. As a class of iterative solvers, Krylov subspace method provides one of the most important tools for solving large sparse linear systems. For SPD matrices, the conjugate gradient (CG) is the uncontested choice because it uses a three-term recurrence to converge optimally, with a minimum of storage and computational requirements [9]. If a coefficient matrix has a large condition number, the convergence of CG method can be significantly improved by the use of a preconditioner. Each system in Eq. (1), as a SPD linear system, can be solved efficiently with a preconditioned conjugate gradient (PCG). For the solution of multiple linear systems, the obvious approach is to solve the linear systems one by one using the PCG method. Such a method regenerates search directions within previously explored subspaces. When the coefficient matrices are close, sharing information between systems is expected to be more effective. One possible way to obtain the solution of multiple linear systems by sharing information between systems is to use the block approach [9-12], but the block method is only available if all the linear systems have the same coefficient matrix. Recycling subspace is another technique to share information between systems for the solution of multiple linear systems [13-18]. It has been successfully employed in combination with the classical Krylov subspace methods to solve various application problems, such as large-scale topology optimization [19], electro- magnetic modeling [20-22], and optical tomography [23].
The goal of this work is to study iterative solvers for the solution of the multiple linear systems in Eq. (1) and to provide several techniques to improve the computational efficiency. Based on the fact that the difference in the multiple linear system matrices is small, the solution of the forward problem is accelerated by means of the recycling Krylov subspace technique. The stiffness matrices are assembled and stored into two parts separately, and the equivalent linear systems which have closer right-hand sides than the original systems are constructed. The recycling strategy is implemented by choosing a system as the seed system and projecting the initial error of other systems onto the generated subspace. The necessary algorithm and program are developed and detailed pseudo-code for the improved algorithm is provided.
2 FEM modeling of DC resistivity
The point source field forward problem is governed by a Poisson equation [6]:
(2)
where σ is the electric conductivity distribution; u is the electrical potential; I is the current source; Ω is the computational domain and δ is the Dirac delta function.
The boundary Γ of domain Ω can be subdivided into a surface parts Γs and a subsurface parts Γ∞. The Neumann boundary condition has to be applied on Γs and mixed boundary conditions have proved to be a reasonable option for Γ∞:
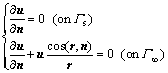(3)
where n is the outward pointing normal vector on the boundary and the vector r represents the distance between the source electrode and the boundary. The equivalent variational problem is given as
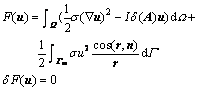(4)
By employing finite element meshes, the domain Ω is subdivided into small regions which are referred to as finite elements. The integral in Eq. (4) can be calculated in each element and on the boundary Γ∞. After discretization, and after having computed and assembled the element stiffness matrices, the variational problem in Eq. (4) leads to a linear system of equations of the form:
(A0+ΔA)u=e (5)
where A0 is associated with the first integral term in Eq. (4), and ΔA, which is inversely proportional to the distance between the source electrode and the boundary, is obtained from the boundary integrals term in Eq. (4). In addition, the right-hand side e only includes the term that depends on the source electrode, and it can be assumed to be a normal vector which has zero components, except for the current magnitude 1 at the current injection location. It has the form (0, 0, …, 0, 1, 0, …, 0)T.
3 Recycling Krylov subspace method for multiple linear systems
The Krylov solver of choice for the solution of large sparse and symmetric positive linear system of the form Ax=b is CG, which constructs the k-th iteration xk in the subspace so that ||x(k)-x*||A is minimized:
x(0)+span{r(0), Ar(0), …, A(k-1)r(0)} (6)
where x* is the exact solution of Ax=b.
The convergence of CG is governed by the distribution of the eigenvalues of A. The smallest eigenvalues of the matrix A often slow down the convergence. This is highlighted by the bound on the rate of convergence of CG [9], which is as follows:
(7)
where e(k)=x*-x(k), denotes the forward error associated with the iteration at step k; κ=κ(A)=λmax/λmin, denotes the condition number of A; and ||x||A=(xTAx)1/2, denotes the A-norm of x. From this bound, it can be seen that increasing the size of the smallest eigenvalues will improve the convergence rate of CG.
In the present problem, when multiple source electrode positions are taken into account, a sequence of linear systems can be obtained:
(A0+ΔAi)ui=ei (i=1, …, s) (8)
where the index i indicates different source electrodes and s is the number of source electrodes. Because ΔAi just includes the boundary integral terms, the coefficient matrices of the multiple linear systems do not differ too much. Therefore, it is hoped to iteratively solve the multiple linear systems more efficiently than it would be if they are treated as s completely unrelated systems. The method is to recycle the subspace information, which is generated by initially solving a linear system, for the solution of the subsequent linear systems.
3.1 Solving seed linear system
The seed projection method generates a Krylov subspace from a set of direction vectors obtained by solving one of the systems, which is called a seed system, by the CG method. The residuals of other systems are then projected onto the generated Krylov subspace to get the initial guess. The whole process is repeated until all the systems are solved [17]. The seed projection method has the superconvergence by virtue of using the projected solution as the initial guess for non-seed systems. The reason is that the projection process kills off the extreme eigenvector components of the initial error. Because the Ritz values approach the extreme eigenvalues rapidly in the first few steps of the Lanczos process, the Krylov subspace generated by the first few steps also contains the extreme eigenvectors. As a result, after the Galerkin projection, the effective spread of the spectrum of A is narrowed, which in turn increases the rate of convergence.
Algorithm 1: The seed projection method [17]
1. for k=1, …, s until all the systems are solved
2. select the k-th system as seed
3. for i=0, 1, 2, …, mk+1 %CG iteration
4. for j=k, k+1, …, s % unsolved systems
It is noted from lines 13-15 in Algorithm 1 that the matrix-vector multiplication 
is required for each projection of the non-seed iteration. The cost of the method will be expensive in the general case where the matrix Aj and Ak are different. CHAN and NG [17] gave another version of seed method that use Ak instead of Aj in lines 13 and 15 to reduce the computation cost. However, the latter algorithm generally leads to slower convergence and lower efficiency. Fortunately, in the present problem, the global stiff matrix Aj is decomposed into two parts as A0+ΔAj and cheaply in the following way:
Firstly, the coefficient matrices are written as
Aseed=A0+ΔAseed, Aj=A0+ΔAj
Then,
(9)
Therefore, can be updated cheaply by adding 
which has been computed in the seed iteration, and 
together. The cost of matrix-vector multiplication is expected to be small. Since (ΔAj-ΔAseed) is only associated with the mesh nodes on the subsurface boundary, it is a low-rank matrix and the number of nonzero entries of (ΔAj-ΔAseed) involved in the calculation is far less than that of Aj by compressed sparse row scheme (CSR).
Furthermore, to use the solution of the seed method as the initial guess for subsequent linear systems, it is preferred to solve the seed system and the subsequent systems separately, and to store the recycling subspace information in 
where span{ } denotes a vector subspace defined as all linear combinations of vectors in bracket. The algorithm for the seed system is given as the follows.
Algorithm 2: Solving the seed linear system
3.2 Solving subsequent linear systems by recycling subspace
After the seed linear system has been solved, the recycling subspace W will be reused to solve the subsequent linear systems. The augmented subspace conjugate gradient method (AugPCG) [18] is a method which uses existing subspace information to speed up the solution of the current systems. It aims at linear systems with the same coefficient matrices and multiple right-hand sides. The ideas similar to those presented in AugPCG are adopted, where an initial guess x0 is chosen such that the initial residual r0=b-Ax0 is orthogonal to the recycling subspace span{w1, …, wm}, and the current descent direction pi is forced to be A-orthogonal to the last vector wm in W. The orthogonalization is implemented by a modified Gram-Schmidt process. Additionally, the solution of the seed system xseed is used as an initial approximation. The algorithm for the solution of the nonseed systems of Eq. (8) is given below, in which (,) denotes a vector dot product.
Algorithm 3: Solving the nonseed linear systems
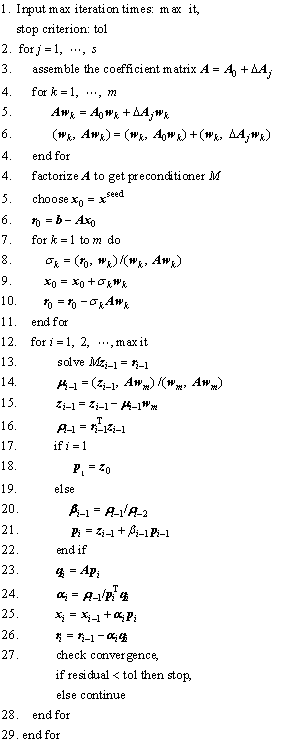
3.3 Equivalent multiple linear systems with more related right-hand sides
If the right-hand sides of multiple linear systems are close to each other, the seed method is expected to be more effective. However, the right-hand sides in Eq. (8) have the form as ei=(0, …, 0, 1, 0, …, 0)T, from which we can deduce that (ei, ej)=0 and cos(ei, ej)=(ei, ej)/ (||ei||2||ej||2)=0 when i≠j, which means that they are orthogonal to each other. Here, a technique is addressed to overcome the problem. An equivalent multiple linear system is constructed instead of Eq. (8), and the recycling subspace method is applied to the new linear systems.
Assuming that the k-th system is chosen as a seed system, the equivalent linear systems are constructed as
(10)
where b0=(1, 1, …, 1)T, is a vector which has all components equal to 1.
Let bi=(1, 1, …, 1, 0, 1, …, 1)T be a vector which has 1 in all components except for the current magnitude 0 at the current injection location i. It is easy to see that
(i=1, 2, …, s) (11)
and
(12)
where nd is the dimension of the coefficient matrix, ei and ui are the right-hand sides and the unknown vectors given in Eq. (8), respectively. Because (ΔAi-ΔAk) is small, Eq. (12) indicates that a larger nd means the right- hand sides are closer and, therefore, there is better iteration convergence. This implication has also been verified by the numerical experiments in Section 4. There is only one drawback of the method that we have to solve the seed system twice to get uk. However, the extra cost is worthwhile when considering hundreds of linear systems that need to be solved.
3.4 Numerical implementation
A Fortran program is developed based on the above analysis. A simplified flowchart for solving the multiple linear systems is shown in Fig. 1.
A few remarks about the improved algorithm can be made as follows:
1) The problem considered here is that the multiple source electrodes are employed, and the computation domain is discretized just once to obtain the electrical potential values of all the grid nodes. This leads to solving a multiple linear system. The coefficient matrices differ from low-rank matrices which are only associated with the boundary integral. Therefore, the coefficient matrices do not differ very much.
Fig. 1 Flow chart of solving process for multiple linear systems
2) The coefficient matrices are separated into two parts: one is A0, which is associated with the volume integral; the other is ΔAi, which is associated with the boundary integral. In the practical implementation, we only need to store the A0 and ΔAi (i=1, …, s). Because ΔAi is a low-rank matrix, this scheme also reduces the storage requirement, in addition to reducing the computational cost as per the analysis in Section 3.1.
3) The degree of the difference between the matrices of the seed system and the nonseed systems is relative to the distance between the locations of the relevant source electrodes. When the distance becomes too large, the seed system needs to be reselected to restart the same procedure.
4) Note that storing m vectors in W, which is generated in the seed system, is required. If the scale of the problem is very large and m is chosen to be large, this may cause a memory requirement problem. In this case, the seed system and the subsequent systems can be solved simultaneously, as shown in Algorithm 1, but the yseed is not available for input as an initial guess when the subsequent systems are solved.
4 Numerical results
Numerical simulations were carried out for two different models: a homogeneous conductivity model and a 2D vertical contact model. The results were obtained on a PC with an Intel(R) Core?2 Duo T7500 2.20 GHz processor, 2 GB of RAM, and the Windows XP operation system. The experiments were performed in Compaq Visual Fortran 6.6.0. The stopping criterion for the linear system solver is that the relative residual ||b-Axj||/||b||<10-8.
1) The first example is the homogeneous conductivity model with a background resistivity of 200 Ω·m. A numerical discretization with 707 188 elements and 130 736 degrees of freedom is considered. There are also 26 uniformly positioned nodes, which are regarded as point electrodes, and they are located along the x-axis from x=-200 m to x=0 m. The first system (x=0) is taken as the seed system. The numerical results are shown in Table 1 and Fig. 2.
Table 1 Comparison of different schemes for multiple linear systems
Method I solves all the linear systems one by one using PCG, where a zero vector is taken as the initial guess. Method II solves the original linear systems as the form of Eq. (8) with recycling subspace m=122 (this number is equal to the number of the iterations in the seed system), and a zero vector is taken as the starting guess for all the systems. Method III solves the original linear systems with recycling subspace m=122, where a zero vector is taken as the starting guess for the seed system, and the solution of the seed system is taken as the starting guess for the subsequent systems. Method IV solves the equivalent linear systems as the form of Eq. (10) with recycling subspace m=142 (this number is equal to the number of the iterations in the seed system), where a zero vector is taken as the starting guess for all the systems. Method V solves the equivalent linear systems with recycling subspace m=142. As before, a zero vector is taken as the starting guess for the seed system, and the solution of the seed system is taken as the starting guess for the subsequent systems.
Table 1 shows the CPU time required for convergence of all 26 linear systems using different solving schemes. Method I solves all of the systems one by one using PCG without recycling a subspace. It can be seen that the methods require 285.9 s of CPU time to solve all the systems. Method II and III use PCG to solve the seed system and recycle a subspace generated in the seed system to solve the subsequent system. It can be seen that the performance has been improved, but not very much. Method IV and V transform the original multiple linear systems into more-related systems by the method given in Section 3.3, and method V chooses the solution of the seed system as an initial guess for the subsequent systems. It is shown that method V provides the best performance and it requires 145.1 s CPU time for all the 26 linear systems. Despite the fact that it needs to solve the seed system twice, the computational time is reduced by almost 50%, compared with that for method I. The results clearly reveal that the costs are effectively reduced when the improved techniques are employed.
Figure 2 shows the convergence behaviour of all the systems solved by the methods I and V. In the plot, each of the steepest declining lines denotes the convergence of a system. The relative residual norm is plotted against the iteration number. It is shown that, when the equivalent systems are solved in the form of Eq. (10) instead of the original system and when the solution of the seed system is used as an initial approximation for the non-seed systems, the algorithm reduces the initial residual and the iteration number of the subsequent systems greatly, thus reduces the total computational cost, although it requires more iteration numbers to solve the seed system.
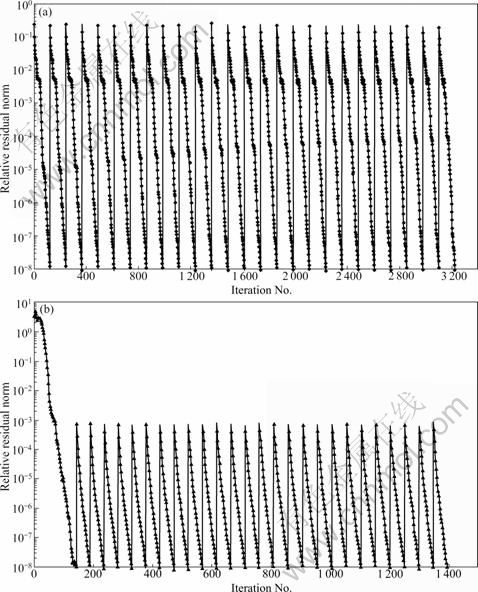
Fig. 2 Relative residual norm per system solving results computed using different methods: (a) Method I; (b) Method V
2) The second example is a 2D vertical contact model with resistivity ρ1=10 Ω·m on the left-hand side and ρ2=200 Ω·m on the right-hand side. Pole-pole measure equipment is employed. The measure line is along the x-axis from x=-250 m to x=250 m, and the distance between point source and measure point is 10 m. A numerical discretization with 918 011 elements and 166 579 degrees of freedom is considered. Additionally, 51 linear systems need to be solved. Two methods are adopted: (1) PCG: to solve all the systems one by one using by PCG, a zero vector is taken as the starting guess; (2) Recycled PCG: a recycling subspace is combined with m=159 (the number of iterations required for the seed system) with related right-hand techniques and the solution of the seed system (corresponding to the source point x=0) is used as the initial guess for the nonseed systems. In addition, a zero vector is taken as the starting guess for the solution of the seed system. Figure 3 shows the model and a comparison of the analytical and numerical solutions with PCG and recycled PCG. It can be seen that the results from the two methods agree with the analytical solution very well, and the maximum relative error is 2%. Figure 4 shows the degree of difference between the non-seed coefficient matrix and the seed coefficient matrix. The number of iterations and CPU time spent in solving all the linear systems are shown in Fig. 5. It can be seen that the improved algorithm reduces the solution time and the number of iteration for the non-seed system. Furthermore, it is also observed that recycling works more efficiently for the systems which have closer coefficient matrices to the seed system. Therefore, a new seed system should be chosen if the unsolved systems are far from the seed system.
Fig. 3 Comparison of analytical solution and numerical solution over a vertical contact
Fig. 4 Infinite norm of (Ai-Aseed) (i=1, 2, …, 54)
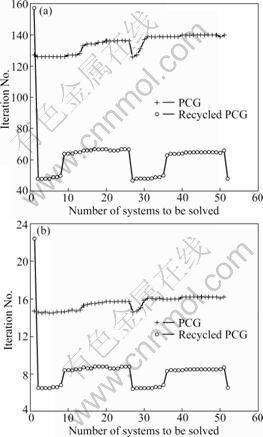
Fig. 5 Iterations per system of solution (a) and CPU time per system of solution (b)
5 Conclusions and future work
1) Some schemes are presented to improve the computational efficiency for the 3D FEM modeling of DC resistivity. The global stiff matrices are considered to be assembled and stored in two parts separately. The equivalent multiple linear systems with closer right-hand sides are constructed and the recycling Krylov subspace technique for the multiple linear systems is implemented by solving a seed system first. Then, the descent direction and the solution of the seed system is reused to accelerate the process of finding the solution of the subsequent systems.
2) Detailed pseudo-code and a Fortran program that implements the improved algorithm has been developed. Various strategies to improve the performance of the solution of the multiple linear systems are discussed. The results of numerical examples show that the improved method has a favorable performance.
3) The parallelization of the implementation is not considered in this work. In future work, the authors intend to parallelize the solution of the FEM equations based on the improved algorithm to implement the 3D fast inversion.
References
[1] DEY A, MORRISON H F. Resistivity modeling for arbitrarily shaped three-dimensional structures [J]. Geophysics, 1979, 44(4): 753-780.
[2] LI Y, SPITZER K. Three-dimensional DC resistivity forward modeling using finite elements in comparison with finite-difference solutions [J]. Geophys J Int, 2002, 151(3): 924-934.
[3] RUAN B Y, XIONG B, XU S Z. Finite element method for modeling resistivity sounding 3-D geo-electric section [J]. Earth Science-Journal of China University of Geosciences, 2001, 26(1): 73-77.
[4] TANG J T, REN Z R, HUA X R. Triangle and tetrahedral finite element meshing from arbitrary geophysical model data [J]. Progress in Geophysics, 2006, 21(4): 1272-1280. (in Chinese)
[5] WU X P, WANG T T. A 3D finite element resistivity forward modeling using conjugate gradient algorithm [J]. Chinese Journal of Geophysics, 2003, 46(3): 428-432. (in Chinese)
[6] XU S Z. The finite element method in geophysics [M]. Beijing: Science Press, 1994: 173-183. (in Chinese)
[7] R?CKER C, G?NTHER T, SPITZER K. Three-dimensional modeling and inversion of dc resistivity data incorporating topography: I. Modeling [J]. Geophys J Int, 2006, 166(2): 495-505.
[8] BLOME M, MAURER H R, SCHMIDT K. Advances in three-dimensional geoelectric forward solver techniques [J]. Geophys J Int, 2009, 176(3): 740-752.
[9] SAAD Y. Iterative methods for sparse linear systems [M]. 2nd Edition. Society for Industrial and Applied Mathematics, 2003.
[10] ?LEARY D P. The block conjugate gradient algorithm and related methods [J]. Linear Algebra Appl, 1980, 29: 293-322.
[11] FREUND R W, MALHOTRA M. A block QMR algorithm for non-Hermitian linear systems with multiple right-hand sides [J]. Linear Algebra Appl, 1997, 254(1): 119-157.
[12] MORGAN R B. Restarted block-GMRES with deflation of eigenvalues [J]. Appl Numer Math, 2005, 54(2): 222-236.
[13] PARKS M L, de STURLER E, MACKEY G, et al. Recycling Krylov subspaces for sequences of linear systems [J]. SIAM Journal on Scientific Computing, 2006, 28(5): 1651-1674.
[14] GIRAUD L, RUIZ D, TOUHAMI A. A comparative study of iterative solvers exploiting spectral information for SPD systems [J]. SIAM Journal on Scientific Computing, 2006, 27(5): 1760-1786.
[15] SALKUYEH D K. CG-type algorithms to solve symmetric matrix equations [J]. Applied Mathematics and Computation, 2006, 172(2): 985-999.
[16] GOLUB G H, RUIZ D, TOUHAMI A. A hybrid approach combining Chebyshev filter and conjugate gradient for solving linear systems with multiple right-hand sides [J]. SIAM J Matrix Anal Appl, 2007, 29(3): 774-795.
[17] CHAN T F, NG M K. Galerkin projection methods solving multiple linear systems [J]. SIAM Journal on Scientific Computing, 1999, 21(3): 836-850.
[18] ERHEL J, GUYOMAR?H F. An augmented conjugate gradient method for solving consecutive symmetric positive definite linear systems [J]. SIAM J Matrix Anal Appl, 2000, 21(4): 1279-1299.
[19] WANG S, DE STURLER E, PAULINO G H. Large-scale topology optimization using preconditioned Krylov subspace methods with recycling [J]. Int J Numer Meth Engng, 2007, 69(12): 2441-2468.
[20] JIN C, CAI X C. A preconditioned recycling GMRES solver for Stochastic Helmholtz problems [J]. Commun Comput Phys, 2009, 6(2): 342-353.
[21] CLEMENS M, HELIAS M, STEINMETZ T, WIMMER G. Multiple right-hand side techniques for the numerical simulation of quasistatic electric and magnetic fields [J]. Journal of Computational and Applied Mathematics, 2008, 215(2): 328-338.
[22] MELLO L A M, de STURLER E, PAULINO G H, SILVA E C. Recycling Krylov subspaces for efficient large-scale electrical impedance tomography [J]. Comput Methods Appl Mech Engrg, 2010, 199(49): 3101-3110.
[23] KILMER M E, de STURLER E. Recycling subspace information for diffuse optical tomography [J]. SIAM Journal on Scientific Computing, 2006, 27(6): 2140-2166.
(Edited by HE Yun-bin)
Foundation item: Projects(40974077, 41164004) supported by the National Natural Science Foundation of China; Project(2007AA06Z134) supported by the National High Technology Research and Development Program of China; Projects(2011GXNSFA018003, 0832263) supported by the Natural Science Foundation of Guangxi Province, China; Project supported by Program for Excellent Talents in Guangxi Higher Education Institution, China; Project supported by the Foundation of Guilin University of Technology, China
Received date: 2011-01-07; Accepted date: 2011-05-19
Corresponding author: XIONG Bin, Professor, PhD; Tel: +86-15807736272; E-mail: xiongbin@glite.edu.cn
