椭圆形截面织构的最优参数设计模型
马晨波1,朱华2,孙见君1
(1. 南京林业大学 机械电子工程学院,江苏 南京,210037;
2. 中国矿业大学 机电学院,江苏 徐州,221116)
摘要:为建立流体润滑状态下表面织构的最优参数设计模型,采用求解表面织构润滑计算模型的方法研究织构参数和工况参数对摩擦因数的影响规律。研究结果表明:最优织构直径越大,其对应的最优织构深度也越大;深径比参数不能作为织构尺寸参数对摩擦因数影响的唯一表征,即织构直径和深度2个参数应分别进行研究,但当深径比在0.005~0.01之间时,不论织构直径和深度如何,其对应的摩擦因数均较小;最优织构面积比与织构尺寸参数及工况参数无关;载荷越大,速度越小,对应的最优织构深度越小,而最优织构直径越大。在仿真结果的基础上,建立椭圆形截面织构的最优参数设计模型,并对模型进行试验验证和应用分析。
关键词:表面织构;最优参数设计模型;摩擦因数
中图分类号:TH117 文献标志码:A 文章编号:1672-7207(2012)03-0953-07
Optimal design model of surface texture with elliptical shape
MA Chen-bo1, ZHU Hua2, SUN Jian-jun1
(1. College of Mechanical and Electrical Engineering, Nanjing Forestry University, Nanjing 210037, China;
2. School of Mechanical and Electrical Engineering, China University of Mining and Technology, Xuzhou 221116, China)
Abstract: In order to establish the optimal design model of textured surface under hydrodynamic lubrication, the influence of parameters of surface texture and operation conditions on friction coefficient was studied by solving lubrication computation model of surface texture. The results show that the optimal depth increases with the increase of the optimal diameter of surface texture; the ratio of depth to diameter can not be used as the only characterization size parameter on the effect of friction coefficient and the influence of depth and diameter on friction coefficient is studied separately, but when the aspect ratio lies in 0.005 to 0.01, the corresponding friction coefficient is smaller; the optimal area ratio is not bound up with the parameters of surface texture and operation conditions; the larger the load and the smaller the velocity, the smaller the corresponding optimal depth while the larger optimal diameter of surface texture becomes. An optimal design model of surface texture with an elliptical shape is established based on the computational results, and the validation as well as the application problem of the model are also presented.
Key words: surface texture; optimal design model; friction coefficient
近年来,在摩擦副表面进行人工微造型的表面织构技术由于能够有效改善表面的摩擦学性能而受到了国内外学者的广泛重视,其在计算机硬盘[1]、轴承和密封[2-3]、发动机系统[4]中也得到了应用。寻找针对具体工况和润滑条件的最优参数是表面织构领域的热点问题,目前的研究大多是从试验的角度针对某一个或几个特定工况条件下开展的。当工况参数改变,其对应的最优织构参数也会随之发生改变,这也是不同学者的研究获得不同最优织构参数的原因。如Schreck等[5]在100Cr6上加工织构后进行摩擦学试验,发现当织构的面积比为55%时其减摩性能越好;Costa等[6]对织构的钢平面试件与无织构的钢圆柱试件在流体润滑状态下的摩擦学性能进行了研究,发现当圆凹坑的面积比在11%时能够获得最大的油膜厚度;Koszela等[7]在铜试件表面加工微凹坑织构,发现在凹坑深度为100 μm,面积比为26%时,摩擦副具有良好的抗擦伤性能。而为了从理论上为表面织构的优化设计提供支撑,有必要开展织构参数之间的相互影响以及工况参数对最优织构参数影响规律的研究,进而建立具有普适性的表面织构最优参数设计模型。因此,本文作者通过求解表面织构的润滑计算模型,研究流体润滑状态下织构参数之间的相互影响以及工况参数对最优织构参数的影响规律。在仿真结果的基础上,建立表面织构的最优参数设计模型,并进而对模型进行试验验证和应用分析。
1 表面织构的润滑计算模型
为简化计算,假设摩擦副两表面中一个为光滑表面,另一个为椭圆形截面织构按一定间距规则排列的表面。取如图1所示的矩形计算单元,以水平面为xoy坐标平面,z方向即为膜厚方向,沿x和y方向的单元
长度分别为L和W,两摩擦副的间隙为h0;对于表面织构,设其最大深度为hp,直径为2rp,面积比为Sp;工况参数中载荷为P,速度为u。
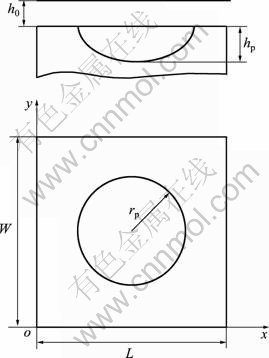
图1 织构微单元示意图
Fig.1 Schematic diagram of surface texture cell
流体润滑状态下表面织构润滑计算模型中所采用的Reynolds方程形式为[8]:
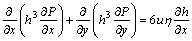 (1)
(1)
采用编程计算不同织构参数和工况参数下的摩擦因数μ。计算中,上下边界处采用对称条件,左右边界处的压力均取为大气压力,采用Reynolds空化边界以考虑可能产生的气穴现象。
2 织构参数之间的相互影响及工况参数对最优织构参数的影响规律
2.1 织构参数之间的相互影响
图2所示为P=1 N和Sp=12.56%条件下,摩擦因数随织构深度和直径的变化。从图2中可以看出:存在最优的织构深度和直径使得摩擦因数最小;而且随着织构直径(或深度)的增大,其对应的最优织构深度(或最优织构直径)随之增大。
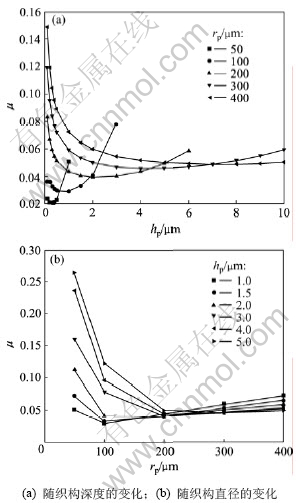
图2 摩擦因数随织构深度和直径的变化
Fig.2 Variation of friction coefficients with depth and diameter of surface texture
大多数学者在研究织构参数对摩擦因数的影响时,引入了深径比参数的概念[9],而不再单独研究织构直径和织构深度的影响。由图2可知:织构直径(或深度)越大,其对应的最优织构深度(或最优织构直径)也越大。从这个意义上讲,采用深径比参数似乎是合理的,但其能否作为织构尺寸参数对摩擦因数影响的唯一表征呢?图3所示为摩擦因数关于织构深径比变化的散点。
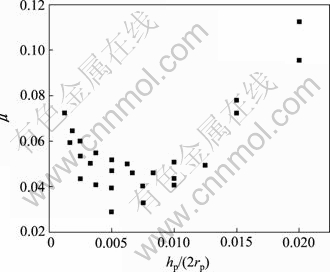
图3 摩擦因数与织构深径比的关系
Fig.3 Friction coefficients vs. depth to diameter ratios of surface texture
从图3可以看出:当其他参数相同,在相同的织构深径比但不同的织构直径或深度条件下,可能对应不同的摩擦因数。因此,深径比参数不能作为织构尺寸参数对摩擦因数影响的唯一表征,织构直径和深度2个参数对摩擦因数的影响规律应分别进行研究。但从图3中还可以看出:当织构深径比的大小在0.005~ 0.01之间时,不论织构的直径和深度如何,摩擦因数均较小。
在不同面积比条件下,摩擦因数随织构深度及直径的变化如图4所示。从图4可以看出:织构面积比的改变并不影响最优织构深度及最优织构直径的 大小。
图5所示为摩擦因数随织构面积比的变化。从图5可以看出:随着织构面积比的增加,摩擦因数呈现先减小后增大的趋势,存在最优的织构面积比Sp=76%,使得摩擦因数最小。
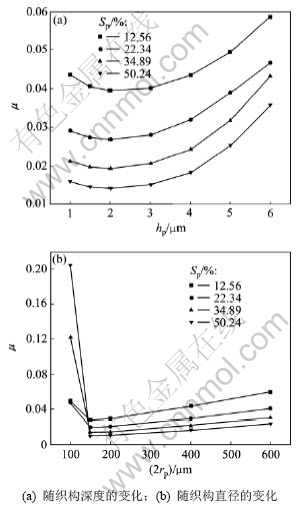
图4 不同织构面积比条件下摩擦因数的变化
Fig.4 Friction coefficients vs. depths and diameters under different area ratios of surface texture
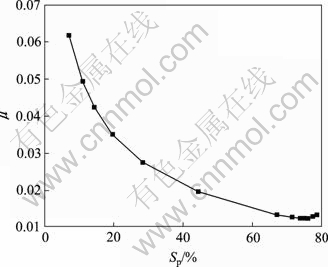
图5 摩擦因数随织构面积比的变化
Fig.5 Friction coefficients vs. area ratios of surface texture
在不同的织构深度和织构直径条件下,摩擦因数随织构面积比的变化如图6所示。从图6可以看出:最优织构面积比不会随着织构深度和直径的变化而改变。
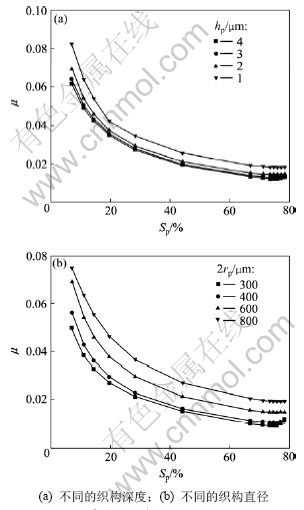
图6 摩擦因数随织构面积比的变化
Fig.6 Friction coefficients vs. area ratios of surface texture
2.2 工况参数对最优织构参数的影响
图7列出了不同载荷条件下,摩擦因数随织构深度、直径及面积比的变化。从图7可以看出:在不同的载荷条件下,均存在最优的织构深度、直径及面积比。而且,载荷越大,最优织构深度越小,最优织构直径越大;而随着载荷的增大,最优织构面积比变化不大,均在76%附近。
在不同速度条件下,摩擦因数随织构深度、直径及面积比的变化见图8。从图8可以看出:在不同的速度条件下,均存在最优的织构深度、直径及面积比。而且速度越大,最优织构深度越大,最优织构直径越小;而最优织构面积比随着速度的增大变化不大,均在76%附近。
3 表面织构最优参数设计模型
3.1 模型的建立
对于表面织构的摩擦学设计,一般所要考虑的影响因素包括织构的形状参数(截面形状)、尺寸参数(深度、直径及面积比)及工况参数(载荷和速度)等。本文所建立的表面织构最优参数设计模型以椭圆形截面织构为基础,考虑织构尺寸参数及工况参数对最优织构参数的影响,一般形式如下:
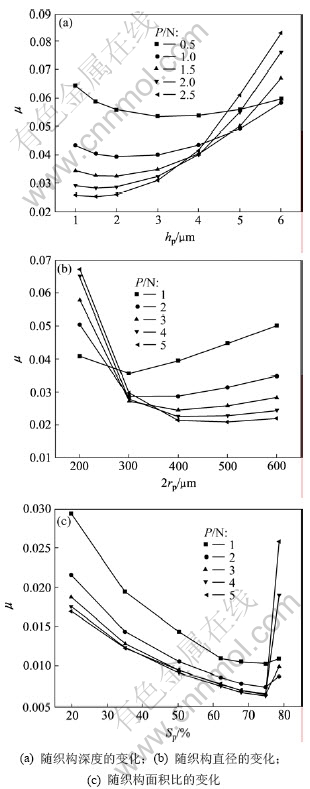
图7 不同载荷下摩擦因数随织构参数的变化
Fig.7 Friction coefficients vs. parameters of surface texture under different loads
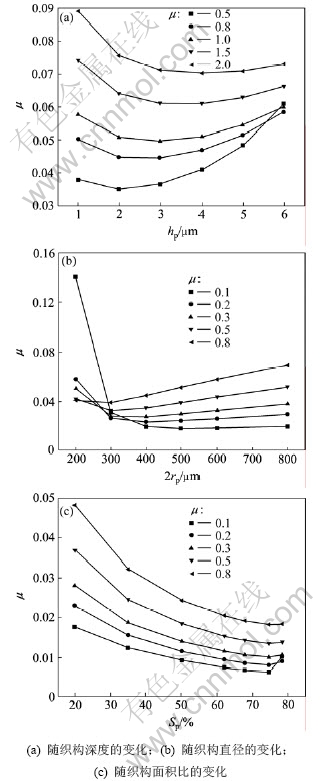
图8 不同速度下摩擦因数随织构参数的变化
Fig.8 Friction coefficients vs. parameters of surface texture under different velocities
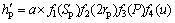 (2)
(2)
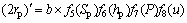 (3)
(3)
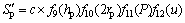 (4)
(4)
式中: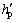 ,
,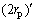 和
和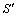 分别为最优织构深度、直径及面积比。
分别为最优织构深度、直径及面积比。
由仿真结果可知:最优织构面积比与织构深度、直径及工况参数不相关;而且最优织构深度和最优织构直径与织构面积比也不相关,因此,式(2)~(4)可以简化为:
 (5)
(5)
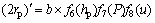 (6)
(6)
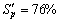 (7)
(7)
然后,在仿真结果得到的最优织构深度值附近进行局部加密计算,求取精确的最优织构深度值,进而获得最优织构深度随织构直径、载荷及速度的变化规律。利用指数曲线y=exp(a0+b0×x+c0×x2)拟合,获得f2,f3及f4的表达式,其拟合可信度均在0.99以上。可得到最优织构深度表达式为:
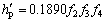 (8)
(8)
其中:
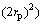 ;
;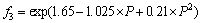 ;
;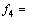
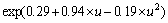 。
。
同理,可得到最优织构直径随织构深度、载荷及速度的变化规律及拟合关系式。其表达式为
 (9)
(9)
其中: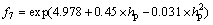 ;
;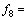
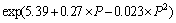 ;
;
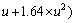 。
。
式(7)~(9)即为基于仿真结果的椭圆形截面织构的最优参数设计模型。为验证设计模型的正确性,需要通过试验的手段来研究织构表面在流体润滑状态下的摩擦学性能表现。
3.2 模型的试验验证及应用分析
摩擦试验在UMT-2型多功能试验机上进行。采用旋转式销-盘试验,上试件固定不动,下试件进行旋转运动。上试件采用GCr15钢销试件,直径为4 mm,硬度为HRC 64。下试件采用Q235钢盘试件,直径为68 mm,厚度为8 mm,硬度为HV 190,试验前对其表面进行抛光处理后的粗糙度Ra为0.05 μm。为尽可能保证销-盘试件的面面接触,试验前将销试样固定在UMT-2摩擦磨损试验机上试件夹具上,将砂纸固定在下试件上,在转速300 r/min和载荷2 N的条件下运转1 min,获得试验前销试样的表面粗糙度Ra为 0.1 μm左右。
采用ZY型电路板制作机的孔加工功能在下试件表面上进行织构的机械加工,通过更换不同直径的钻头获得不同的织构直径,织构的间距和深度则通过计算机精确控制。织构加工完毕后,在抛光机上轻微抛光以除去织构附近的毛刺。通过超高精度三维轮廓仪观察,织构的截面形状接近于椭圆形。
每组试验中盘试件的转速均为300 r/min,对应的线速度为0.38 m/s。共采用2,6,8,14,16和30 N 6种载荷以保证每组试验中接触区域内单个织构微单元承受的理论载荷均为0.5 N。试验在富油条件下进行,所用润滑剂为30号机械油(无添加剂),试验温度为 20 ℃,此时润滑油的黏度为0.098 Pa·s。每组试验持续20 min,记录观察摩擦因数的变化。
图9所示是织构直径为400 μm,织构深度为20 μm和织构直径为600 μm,织构深度为30 μm 2种状态下,当织构面积比为12.56%,35.0%和62.0%时摩擦因数的变化。从图9可以看出:2种状态下的摩擦因数均随着织构面积比的增大而减小,即当织构面积比为62%时表面的减摩性能最优。试验结果与万轶 等[10]得到的试验结果一致,而且最优织构面积比不随织构直径和织构度的变化而变化。

图9 不同织构面积比下摩擦因数的变化
Fig.9 Friction coefficients vs. area ratios of surface texture
鉴于试验条件的限制,试验结果无法直接验证设计模型中式(7)的正确性,但其变化趋势与仿真研究结果相比可以看出,两者具有较好的一致性,这从某种程度上论证了模型的可行性。
在织构直径为600 μm,织构面积比为12.56%条件下,当织构深度分别取5,10,13和15 μm时的摩擦因数的变化如图10所示。从图10可以看出:当织构深度为10 μm时其减摩性能最优。而通过对设计模型中式(8)进行计算后可得其理论最优织构深度为9.5 μm,与试验结果具有较好的一致性。图11所示是织构深度为13 μm,织构面积比为12.56%条件下,当织构面积比为12.56%,35.0%和62.0%时摩擦因数的变化。从图11可以看出:当织构直径为300 μm时其减摩性能最优。而通过对表面织构的最优参数设计模型中式(9)进行计算后可得其理论最优织构直径为312 μm,与试验结果具有较好的一致性,从而也验证设计模型的正确性。
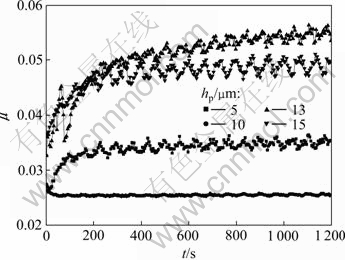
图10 不同织构深度下摩擦因数的变化
Fig.10 Friction coefficients vs. depths of surface texture
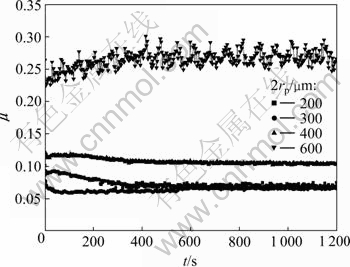
图11 不同织构直径下摩擦因数的变化
Fig.11 Friction coefficients vs. diameters of surface texture
综上,通过对织构表面进行摩擦学试验研究后发现,所建的流体润滑状态下表面织构的最优参数设计模型在一定程度上是合理和正确的。但在应用该模型时应注意以下2个问题:
(1) 模型中以单个织构微单元为研究对象。因此,模型中载荷P应为单个织构微单元所承受力的大小,而不是摩擦副所承受的总载荷;而且实际零件的润滑面尺寸往往有数十微米甚至达数米,而表面织构单个微坑的典型尺寸为数十至数百微米,因此,实际零件的织构表面一般由成千上万个织构微单元组成。那么,基于单个织构微单元的研究结论在整个润滑织构表面的实用性,是需要继续深入研究和探讨的问题。从试验结果来看,当织构间距足够大(试验中织构面积比62.0%以下)以致其间的相互影响可以忽略时,所建的表面织构最优参数设计模型是适用的。
(2) 模型中织构的截面形状为椭圆形。当织构的截面形状发生改变时,最优织构参数设计模型中的常量参数会随之变化。但建立其他织构截面形状时的最优参数设计模型过程与所建椭圆形织构形状时的过程相同。
4 结论
(1) 深径比参数不能作为织构尺寸参数对摩擦因数影响的唯一表征,但当其大小在0.005~0.01之间时,摩擦因数均较小。
(2) 最优织构直径越大,其对应的最优织构深度也越大;最优织构面积比与织构尺寸参数及工况参数不相关。
(3) 载荷越大,速度越小,对应的最优织构深度越小,而最优织构直径越大。
(4) 所建的椭圆形截面织构的最优参数设计模型下的仿真计算结果与试验结果具有较好的一致性,可为表面织构的摩擦学设计提供一定的理论参考。
参考文献:
[1] Hung T A, Wei C S. A novel textured design for hard disk tribology improvement[J]. Tribology International, 2006, 39(6): 506-511.
[2] Brizmer V, Kligerman Y, Etsion I. A laser surface texture parallel thrust bearing[J]. Tribology Transactions, 2003, 46(3): 397-403.
[3] Etsion I. Improving tribological performance of mechanical components by laser surface texturing[J]. Tribology Letters, 2004, 17(4): 733-737.
[4] Ronen A, Etsion I, Kligerman Y. Friction reducing surface-texturing in reciprocating automotive components[J]. Tribology Transaction, 2001, 44(3): 359-366.
[5] Schreck S, Gahr K H Z. Laser-assisted structuring of ceramic and steel surfaces for improving tribological properties[J]. Applied Surface Science, 2005, 247(1/2/3/4): 616-622.
[6] Costa H L, Hutchings I M. Hydrodynamic lubrication of textured steel surfaces under reciprocating sliding conditions[J]. Tribology International, 2007, 40(8): 1227-1238.
[7] Koszela W, Galda L, Dzierwa A, et al. The effect of surface texturing on seizure resistance of a steel-bronze assembly[J]. Tribology International, 2010, 43(10): 1933-1942.
[8] 温诗铸, 黄平. 摩擦学原理[M]. 北京: 清华大学出版社, 2002: 53-54.
WEN Shi-zhu, HUANG Ping. Principles of tribology[M]. Beijing: Tsinghua University Press, 2002: 53-54.
[9] Etsion I, Kligerman Y, Halperin G. Analytical and experimental investigation of laser-textured mechanical seal faces[J]. Tribology Transactions, 1999, 42(3): 511-516.
[10] 万轶, 熊党生. 激光表面微孔化改善端面密封的摩擦学性能[J]. 润滑与密封, 2007, 32(2): 29-31.
WAN Yi, XIONG Dang-sheng. Laser surface-microspored improving tribological properties of face seals[J]. Lubrication Engineering, 2007, 32(2): 29-31.
(编辑 陈爱华)
收稿日期:2011-04-11;修回日期:2011-06-20
基金项目:江苏省属高校自然科学研究面上项目(11KJB460005);国家自然科学基金资助项目(50975276);教育部博士点基金资助项目(20113204120012)
通信作者:马晨波(1983-),男,山东济宁人,博士,讲师,从事表面摩擦学方向的研究;电话:025-85427795;E-mail: mahaibo62@163.com