High-quality trajectory planning for heterogeneous individuals
来源期刊:中南大学学报(英文版)2019年第3期
论文作者:李猛 李石磊 葛渊峥
文章页码:654 - 664
Key words:heterogeneous crowd; trajectory planning; bounded velocity and acceleration; visual variety; authenticity
Abstract: Based on trajectory planning with maximum velocity and acceleration constraints, a novel high-quality trajectory planning method was proposed for heterogeneous individuals in crowd simulation. The proposed method ensured that the individual’s path was smooth and its velocity was continuous. Based on the physiological constraints of humans with maximum velocity and acceleration, time-optimal trajectory and feasible region were derived by solving kinodynamic planning problem. Subsequently, a high-quality trajectory planning algorithm was designed to compute the trajectory with appropriate variation of velocity. The simulation results demonstrate that the proposed trajectory planning method has more authenticities and can generate high-quality trajectories for virtual humans in crowd simulation.
Cite this article as: LI Meng, LI Shi-lei, GE Yuan-zheng. High-quality trajectory planning for heterogeneous individuals [J]. Journal of Central South University, 2019, 26(3): 654–664. DOI: https://doi.org/10.1007/s11771-019- 4036-4.

J. Cent. South Univ. (2019) 26: 654-664
DOI: https://doi.org/10.1007/s11771-019-4036-4
LI Meng(李猛)1, LI Shi-lei(李石磊)2, GE Yuan-zheng(葛渊峥)3
1. Army Academy of Artillery and Air Defense, Hefei 230031, China;
2. Department of Information Security, Naval University of Engineering, Wuhan 430033, China;
3. Communication Countmeasure Department, Aviation University of the Air Force,Changchun 130022, China
 Central South University Press and Springer-Verlag GmbH Germany, part of Springer Nature 2019
Central South University Press and Springer-Verlag GmbH Germany, part of Springer Nature 2019
Abstract: Based on trajectory planning with maximum velocity and acceleration constraints, a novel high-quality trajectory planning method was proposed for heterogeneous individuals in crowd simulation. The proposed method ensured that the individual’s path was smooth and its velocity was continuous. Based on the physiological constraints of humans with maximum velocity and acceleration, time-optimal trajectory and feasible region were derived by solving kinodynamic planning problem. Subsequently, a high-quality trajectory planning algorithm was designed to compute the trajectory with appropriate variation of velocity. The simulation results demonstrate that the proposed trajectory planning method has more authenticities and can generate high-quality trajectories for virtual humans in crowd simulation.
Key words: heterogeneous crowd; trajectory planning; bounded velocity and acceleration; visual variety; authenticity
Cite this article as: LI Meng, LI Shi-lei, GE Yuan-zheng. High-quality trajectory planning for heterogeneous individuals [J]. Journal of Central South University, 2019, 26(3): 654–664. DOI: https://doi.org/10.1007/s11771-019- 4036-4.
1 Introduction
Heterogeneous crowds consist of independent individuals, each with potentially different behavior characteristics and goals. Modeling the behavior of heterogeneous crowds is important in various domains including psychology, robotics, transport engineering and virtual environments [1–3]. The authenticities of single individual’s behavior have a great influence on generating realistic crowd phenomenon. As a result, it is important to realistically model the behaviors of the individuals to generate realistic, heterogeneous crowd behaviors. In terms of modeling the behavior of individuals within a crowd, no matter what approach is used, the proposed approach should consider the following three aspects:
1) In real life, the moving path of a real human is smooth and the velocity is continuous. These two points are the general physiological phenomenon of humans and the basis for generating comfortable locomotion.
2) The resulting variables (e.g. velocity and acceleration) computed by the proposed approach should be in accordance with physiological constraints of humans. Consequently, we must guarantee that they are within the bounds on the maximum velocity and acceleration of humans, i.e. kinodynamic motion planning problem [4, 5].
3) The proposed approach should increase the visual variety of humans in a simulated crowd. Creating variations have the potential to greatly improve the visual authenticities of the output crowd phenomenon [6, 7]. Consequently, it would be more realistic to have variation within the crowd. With respect to a real human in real life, he/she would never keep a constant velocity always in his/her moving from the initial position to the goal, although he/she would not change it quit frequently. From this point, adding appropriate variations to the individual’s velocity can improve the visual authenticities of crowd.
Obviously, a trajectory is seen as the combination of a path and a velocity profile used to move along the path itself. There has been much work which uses planning approaches to synthesize individual’s behaviors. However, most existing works only considered the path planning problem. Actually, trajectory planning, i.e., motion planning problem is the basic problem which should be given intensive studies in heterogeneous crowd simulation, not only the path planning problem. Consequently, creating high-quality trajectories for heterogeneous individuals is indispensable for generating various steering behaviors, e.g., navigational behavior which is the most important behavior in crowd simulation.
Moreover, some researchers have developed approaches aimed at increasing the visual of variety in crowds [6] by increasing the appearance variety of humans or capturing massive motion clips of walking. However, the method which focuses on designing the velocity variety in planning process has not been investigated. Compared with the methods which synthesize variation using motion capture data, our method is realized more easily and needs no extra work to collect massive motion clips.
This paper analyzes and solves a trajectory planning problem for any single individual in heterogeneous crowd. We aim at generating a trajectory for each individual with the following three criteria:
1) On the trajectory, the individual’s path is smooth and its velocity is continuous.
2) The individual’s velocity and acceleration are constrained by the maximum velocity and acceleration respectively.
3) The individual’s velocity contains some varieties which can be used to increase crowd variety.
The proposed method generates high-quality motion trajectory according to the following three- step procedure:
Step 1: We transform the non-smooth path generated by probabilistic roadmap method into smooth one. However, the paths generated by probabilistic roadmap method [8] are normally comprised of a series of nodes and the straight lines which connect them. The shortcoming of these paths is that they are non-smooth and non- differentiable. Humans’ comfortable locomotion can not be generated on this path. Therefore, the non-smooth path will be transformed into smooth one in step 1.
Step 2: A time-optimal trajectory named as “bang-bang trajectory” is computed by converting the dynamic constraints to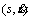 state space. Based on the optimal trajectory, a feasible region is computed.
state space. Based on the optimal trajectory, a feasible region is computed.
Step 3: Under the maximum velocity and acceleration constraints, the feasible region is used to plan a trajectory with appropriate variation of velocity in the 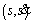 state space.
state space.
After these three steps, a high-quality trajectory is obtained for each individual.
The rest of the paper is organized as follows. In Section 2, we highlight related work in planning methods for crowd simulation. In Sections 3–5, three steps of the trajectory planning problem are described respectively. Specifically, in Section 3, we transform the non-smooth, non-differentiable path which is computed by existing path planning method into a smooth and differentiable path. In Section 4, the optimal trajectory named is computed and Section 5 describes our study on computing the trajectory with appropriate variation of velocity and maximum velocity and acceleration constraints. Section 6 verifies the resulting trajectory computed by our approach. Final conclusions are drawn in Section 7.
2 Related works
Many techniques have been proposed with regard to path planning method for heterogeneous crowd or groups. Among these methods, probabilistic roadmap method (PRM) is used frequently. For example, a flocking behavior method with multiple leaders and a global trajectory was proposed in Ref. [8]. WALLAR et al [9] combined probabilistic roadmaps with potential fields in order to enable a robotic swarm to effectively move to a desired destination while avoiding collisions with obstacles and each other. A novel computational model for representing digital humans was proposed [10]. In this model, human-like agents had their own set of unique capabilities, personalities, and desires. Steering choices were controlled by multi-domain planning with dynamically changing situations.
Also, some works investigated path planning and navigation method for virtual humans based on other graph computing approaches. For example, CHARALAMBOUS et al [11] proposed perception- action graph (PAG) which can be used at run-time to efficiently synthesize believable virtual crowds. KREMYZAS et al [12] presented social groups and navigation (SGN) to simulate the walking behavior of small pedestrian groups in virtual environments. In Ref. [13], pedestrian trajectories that corresponded to the speed/density relationships were generated which can be combined local navigation methods. A series of planning techniques and navigation structures for real-time simulated virtual worlds and computer games were reviewed in Ref. [14]. NORMAN et al [15] presented an extension of (SGN) method to simulate social-group behavior for virtual pedestrians. However, the generated paths were not smooth in the above works.
Based on PRM method, roadmaps for motion planning of multiple agents were created. YAN et al [16] proposed a univector field method-based multi-agent navigation for pursuit problem. Aiming at the asymptotically optimal motion planners,MARBLE et al [17] described a method for interleaving an incremental graph spanner algorithm with the asymptotically optimal PRM algorithm. In order to minimize the complexity in big environments, a new hierarchical path finding solution based on navigation meshes is proposed in Ref. [18]. A planning framework that satisfied multiple spatial constraints imposed on the path including staying behind a building, walking along walls, or avoiding the line of sight of patrolling agents was proposed in Ref. [19]. A high-quality path was computed in which quality can be measured in terms of path length, clearance and smoothness [20]. Aiming at creating smooth paths for camera movement in virtual environment, LINO et al [21] proposed an effective viewpoint interpolation technique based on Toric space which ensured the continuity of perception properties along the generated paths. However, Refs. [16–21] did not pay enough attention to the physiological constraints of humans.
Motion planning methodologies can be classified into two categories: decentralized/indirect and centralized/direct methods [22, 23]. BROGAN et al [24] presented a novel algorithm for simulating proxemic group behaviors using decentralized multi-agent navigation which considered constraints for collision-free navigation and additional connectivity constraints to generate coherent movements. In robotics applications, an obstacle avoidance trajectory planning for an omni- directional robot was investigated in Ref. [25] where obstacles moved with velocity and acceleration constraints. BUTLER et al [26, 27] proposed an optimal, exact planner for optimal bounded- acceleration trajectories along a fixed, given path with dynamic obstacles.
However, the approach designed in Refs. [24– 27] only aimed to generating collision avoidance behavior in crowded scenes and no variation of velocity was considered. As is known to all, the computation cost of centralized motion planning is very expensive and only can be used in schemes that are sensitive to solution quality but insensitive to computation time. In this paper, the decentralized motion planning idea is adopted due to its high efficiency and convenience for online implementation. At the same time, from the perspective of visualization, less computation cost is required.
3 Generating smooth paths for individuals
In Step 1, a smooth path for each individual is generated, the detail of which is depicted in Figure 1.
As illustrated in Figure 1, the non-smooth path for any one individual consists of a series of nodes and the edges connecting any two neighboring ones. Rβ is the radius which is specified by users, its span of value is 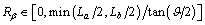 which ensures that the arc will only replace half of the edges at most. When the arc collides with the obstacles, we must decrease Rβ to prevent it. La and Lb are lengths of the two consecutive edges respectively, β is the degree between the two
which ensures that the arc will only replace half of the edges at most. When the arc collides with the obstacles, we must decrease Rβ to prevent it. La and Lb are lengths of the two consecutive edges respectively, β is the degree between the two
consecutive edges and 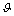 is equal to 180–β. The length of the generated circle arc (denoted as Lβ) is
is equal to 180–β. The length of the generated circle arc (denoted as Lβ) is 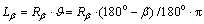 . And we denote the smooth path as S. Obviously, S is comprised of linear part and circle arc part.
. And we denote the smooth path as S. Obviously, S is comprised of linear part and circle arc part.
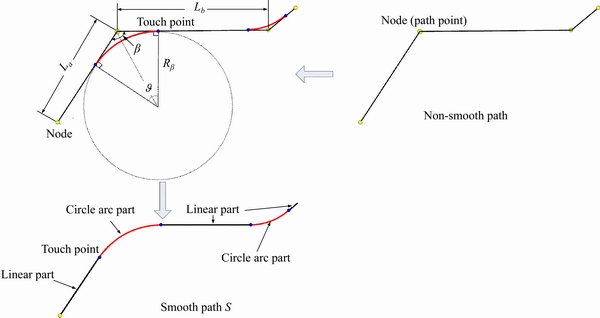
Figure 1 Process of generating a smoothing path
After the smoothing process, S is continuous and differentiable which gives us great conveniences to create continuous and differentiable velocity for the individual.
In fact, the smooth path S produced in this paper is similar to the Dubins curve, which is the shortest path curve connecting any two points in the same plane with a specific direction vector under certain curvature conditions. B-spline and Bezier curve also are the commonly used smooth curves in trajectory planning. However, they are not adopted mainly based on the following two reasons. Firstly,it has been found that people do not always follow a straightest route to their goals. Their walking path in turning is similar to a smooth, circular path with a non-zero minimum turning radius constraint [23]. The second and most important reason is that B-spline and Bezier curves are more complex than S. Even with quadratic B-spline or Bezier curve (parabola), it is still very complicated to derive the current position coordinate of an individual from the distance along the curve, rather than as simple and straightforward as formulae (5) and (10) illustrated in the next section. Therefore, compared with B-spline and Bezier curve, the smoothing method adopted in this paper is appropriate.
4 Computing time-optimal trajectory and feasible region
Time-optimal trajectory is also named as “bang-bang trajectory”. In this section, at first we describe some theoretical results when the individual moves along the smooth path. Then the algorithm of time-optimal trajectory is given and finally the feasible region is computed.
4.1 Converting dynamic constraints into state space and problem statement
Suppose the virtual humans are simplified into cylinder with a unified radius. It is assumed that they move in the workspace 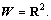 Then, the configuration of the individual is uniquely defined by the triple
Then, the configuration of the individual is uniquely defined by the triple 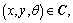 where
where 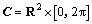 denotes the configuration space. Because the symmetrical characteristic in geometry, we can use q=(x, y) to represent the individual’s configuration.
denotes the configuration space. Because the symmetrical characteristic in geometry, we can use q=(x, y) to represent the individual’s configuration.
The smooth path S generated in Figure 1 can be rewritten as function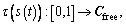 the configuration of the individual at time t is
the configuration of the individual at time t is 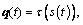 s(t) is the time scaling function
s(t) is the time scaling function  which assigns an s value to each time
which assigns an s value to each time 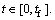 Together, a path and a time scaling specify a trajectory
Together, a path and a time scaling specify a trajectory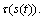 We suppose
We suppose 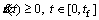 which ensures that the agent will not move backward, i.e., it always moves forward or stays still. LS is defined as the total length of the smooth path S. Then s·LS represents the distance traveled along S.
which ensures that the agent will not move backward, i.e., it always moves forward or stays still. LS is defined as the total length of the smooth path S. Then s·LS represents the distance traveled along S.
The velocity v(t) and acceleration a(t) of the individual can be written as:
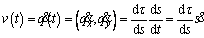 (1)
(1)
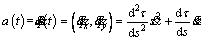 (2)
(2)
According to the dynamic constraints  SUB>
SUB>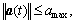 the individual must satisfy the following two equations:
the individual must satisfy the following two equations:
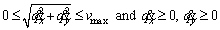 (3)
(3)
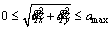 (4)
(4)
where vmax and amax are the maximum velocity and acceleration values a real human can achieve. In Figure 2, we construct a local coordinate system for S.
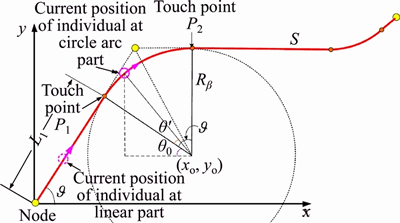
Figure 2 Illustration of local coordinate and current position of individual
For easily converting the dynamic constraints to  state space, origin of coordinate is set at the initial position of the individual. And we parallel X axis of the local coordinate to one linear edge as illustrated in Figure 2. The current position of the individual is classified into two cases.
state space, origin of coordinate is set at the initial position of the individual. And we parallel X axis of the local coordinate to one linear edge as illustrated in Figure 2. The current position of the individual is classified into two cases.
Case 1: The current position of the individual is at the linear part of S.
Take the first linear part (0≤s≤L1/LS) as example, the configuration of the individual can be represented as
 (5)
(5)
Substituting Eq. (5) into Eqs. (1) and (2), we get
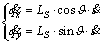 (6)
(6)
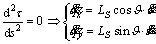 (7)
(7)
Substituting Eqs. (6) and (7) into dynamic constraints Eqs. (3) and (4), we get
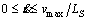 (8)
(8)
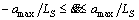 (9)
(9)
Similarly, when the individual is at the other linear part of S, the same results are obtained.
Case 2: The current position of the individual is at the circle arc part of S.
Take the first circle arc part 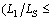
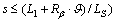 as an example; the configuration of the individual can be represented as:
as an example; the configuration of the individual can be represented as:
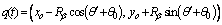 (10)
(10)
where 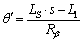 and θ0 are depicted in Figure 2. Substituting Eq. (10) into Eqs. (1) and (2), the following equations hold:
and θ0 are depicted in Figure 2. Substituting Eq. (10) into Eqs. (1) and (2), the following equations hold:
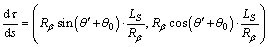
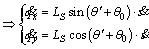 (11)
(11)
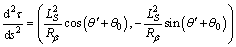
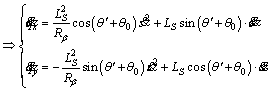 (12)
(12)
Substituting Eqs. (11) and (12) into dynamic constraints Eqs. (3) and (4), we get:
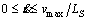 (13)
(13)
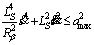
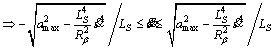 (14)
(14)
According to Eq. (14), we have
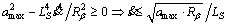 (15)
(15)
Thus,
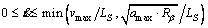 (16)
(16)
According to the principles of circular motion, 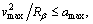 we get
we get 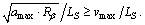 Then Eq. (16) is simplified into Eq. (8).
Then Eq. (16) is simplified into Eq. (8).
Also, when the individual is at the other circle arc part of S, the same results are obtained. So, summing up above formulations, the following conclusions hold.
1) For the first case, the dynamic constraints in Eqs. (3) and (4) are converted to Eqs. (8) and (9).
2) For the second case, the dynamic constraints in Eqs. (3) and (4) are converted to Eqs. (8) and (14).
Consequently, we convert our motion planning problem in Section 1 into the following problem in 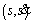 state space.
state space.
Problem statement:
Given the path  an initial state
an initial state 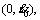 and a final state
and a final state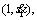
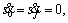 find a trajectory profile
find a trajectory profile 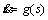 in
in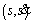 state space that 1) satisfies
state space that 1) satisfies 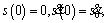
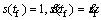 2) ensures that
2) ensures that 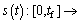
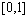 is a monotonically increasing time scaling, i.e., s is a monotonically increasing function of
is a monotonically increasing time scaling, i.e., s is a monotonically increasing function of 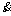 , 3) respects the constraints in Eqs. (8), (9), (14) for all time, and 4) possesses velocity varieties.
, 3) respects the constraints in Eqs. (8), (9), (14) for all time, and 4) possesses velocity varieties.
4.2 Computing time-optimal trajectory and feasible region
We can conveniently visualize the time- optimal trajectory in the 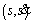 state space as illustrated in Figure 3.
state space as illustrated in Figure 3.
According to the time-scaling algorithm of trajectory planning in Ref. [5], a time-optimal trajectory subject to the constraints in Eqs. (8), (9) and (8), (14) can be computed by replacing
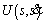 with
with 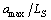 and
and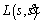 with
with 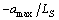 in the linear part and replacing
in the linear part and replacing 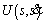 with
with 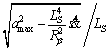 and
and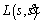 with
with 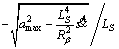 in the circle arc part, also replacing the velocity limit curve v(s) with
in the circle arc part, also replacing the velocity limit curve v(s) with 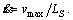
The time-optimal trajectory in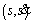 state space is depicted in Figure 3. Then the feasible region (the region filled with lattice in Figure 3) is the region surrounded by
state space is depicted in Figure 3. Then the feasible region (the region filled with lattice in Figure 3) is the region surrounded by 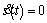 and the time-optimal trajectory. This region has a biggest area compared with any other trajectory which satisfies the constraints in Eqs. (8), (9), (14). So the word “feasible” means that all the trajectories which satisfy the constraints in Eqs. (8), (9), (14) must be in this region. Obviously, the feasible region restricts the scope of our designed trajectory with appropriate variation of velocity.
and the time-optimal trajectory. This region has a biggest area compared with any other trajectory which satisfies the constraints in Eqs. (8), (9), (14). So the word “feasible” means that all the trajectories which satisfy the constraints in Eqs. (8), (9), (14) must be in this region. Obviously, the feasible region restricts the scope of our designed trajectory with appropriate variation of velocity.
5 Planning trajectory with appropriate variation of velocity
In Section 3, we have made dτ/ds continuous and it will not change when the smooth path S is specified. Consequently, from Eq. (1), we can conclude that if we want 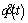 to be continuous, one intuitive way is to make
to be continuous, one intuitive way is to make 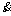 continuous. Moreover, we must make some diversifications in
continuous. Moreover, we must make some diversifications in 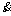 to create appropriate variation of velocity.
to create appropriate variation of velocity.

Figure 3 Constraints in 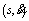 state space
state space
Because 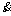 is integration of
is integration of  So the problem of generating variation of velocity is converted into designing appropriate changes to
So the problem of generating variation of velocity is converted into designing appropriate changes to  Consequently, variation of velocity means that the differential of velocity, i.e.,
Consequently, variation of velocity means that the differential of velocity, i.e., 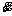 should change with an appropriate frequency.
should change with an appropriate frequency.
In our approach, we use a parameter m0 to represent the maximum number of times which 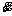 changes in the designed trajectory. So the word “appropriate” means that m0 should be set neither too small nor too large. If m0 is too small, variety will lose. Conversely, if m0 is too large, the individual will change its acceleration too frequently, which results in a frequent changes in its velocity. That is not the case for a human in real life. In general, by introducing m0 and simultaneously taking the feasible region and the constraints in Eqs. (8), (9), (14) for consideration, the time-scaling algorithm is adapted to create high-quality trajectory. Our trajectory planning algorithm is stated as follows.
changes in the designed trajectory. So the word “appropriate” means that m0 should be set neither too small nor too large. If m0 is too small, variety will lose. Conversely, if m0 is too large, the individual will change its acceleration too frequently, which results in a frequent changes in its velocity. That is not the case for a human in real life. In general, by introducing m0 and simultaneously taking the feasible region and the constraints in Eqs. (8), (9), (14) for consideration, the time-scaling algorithm is adapted to create high-quality trajectory. Our trajectory planning algorithm is stated as follows.
Algorithm 1: High-quality trajectory planning algorithm
Input: Smooth path S; 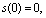
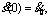
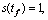
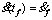 ; parameter m0.
; parameter m0.
Output: Trajectory profile 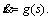
Constraint: 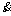 must be continuous; constraints in Eqs. (8), (9), (14); all states
must be continuous; constraints in Eqs. (8), (9), (14); all states 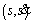 on the trajecroty profile must be in feasible region; s is a monotonically increasing function of
on the trajecroty profile must be in feasible region; s is a monotonically increasing function of 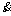 .
.
/* Steps 1–10 are forward integration from the initial state, integral interval is set as [0, s1]. */
1
Let 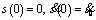 .
.
2
If 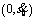 is at the circle arc part of S
is at the circle arc part of S
3
 select a random value from
select a random value from 
4
else  select a random value from
select a random value from  /*
/*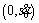 is at the linear part of S*/
is at the linear part of S*/
5
end if
6
 select a value selected from (0, 0.25).
select a value selected from (0, 0.25).
7
Apply forward integration  from
from 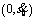 until the integral length on S axis is equal to s1. We call the profile in this stage P0.
until the integral length on S axis is equal to s1. We call the profile in this stage P0.
8
If P0 is in the feasible region, go to step 11.
9
Else decrease s1 and go to step 7.
10
End if
/* steps 11–17 are backward integration from the final state, integral interval is set as 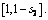 */
*/
11
Let 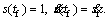
12
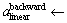 select a random value as in steps 3–4 by verifying
select a random value as in steps 3–4 by verifying 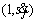 is at the circle arc part or linear part of S.
is at the circle arc part or linear part of S.
13
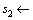 select a value selected from (0, 0.25).
select a value selected from (0, 0.25).
14
Apply backward integration 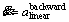 from
from  until the integral length on S axis equal to s2. We call the profile in this stage Pf.
until the integral length on S axis equal to s2. We call the profile in this stage Pf.
15
If Pf is in the feasible region, go to step 18.
16
Else decrease s2 and go to step 14.
17
End if
/* Steps 18–28 are used to plan a trajectory with appropriate variation of velocity using m0. */
18
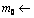 select a random value from [2, 10]. /* we need
select a random value from [2, 10]. /* we need 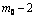 integrations in
integrations in 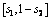 */
*/
19
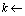 1,
1, 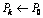
20
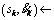 the end state of Pk.
the end state of Pk.
21
If 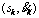 is at the circle arc part of S
is at the circle arc part of S
22
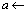 select a random value from
select a random value from 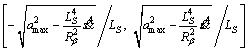 .
.
23
Else 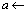 select a random value from
select a random value from 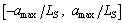 .
.
24
End if
25
Integrate 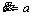 forward from
forward from 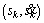 until the integral length on S axis equal to △sk and obtain profile in this stage Pk.
until the integral length on S axis equal to △sk and obtain profile in this stage Pk.
26
If Pk is in the feasible region, k=k+1.
27
If k=m0–3, go to step 29, else go to step 20.
28
Else decrease △sk and go to step 20.
/* step 29 are used to create Pm0–2 by connecting the end of Pm0–3 with the start of Pf. */
29
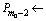 using a line to connect the end of Pm0–3 with the start of Pf
using a line to connect the end of Pm0–3 with the start of Pf
30
Return the profile series {P0, P1, …, Pm–2, Pf}. /* the end of Algorithm 1. */
Algorithm 1 generates a trajectory profile 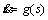 consisting of profile series {P0, P1, …, Pm–2, Pf}. And we select s1, s2 from (0, 0.25) to ensure that s1+s2<0.5. Then there is enough interval in [s1, 1–s2] to design the profile series {P1, …, Pm–2} which is the key to generate the trajectory with variation of velocity. In addition, selecting m0 from [2, 10] is to create appropriate variation i.e., prevent the individual from changing
consisting of profile series {P0, P1, …, Pm–2, Pf}. And we select s1, s2 from (0, 0.25) to ensure that s1+s2<0.5. Then there is enough interval in [s1, 1–s2] to design the profile series {P1, …, Pm–2} which is the key to generate the trajectory with variation of velocity. In addition, selecting m0 from [2, 10] is to create appropriate variation i.e., prevent the individual from changing 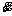 too frequently.
too frequently.
6 Experimental results
In this section, we present several experimental results of the proposed approach in 3D environment in which the agents of the group move on a 2D plane. In our experiments, the smooth path is the same as in Figure 2, which is comprised of three line segments and two circle arc segments. The length of the three linear parts is set as 10, 10 and 2 m, respectively. 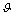 and Rβ of the two circle arc parts is set as 45°, 60°, 7 m, 3 m. So,
and Rβ of the two circle arc parts is set as 45°, 60°, 7 m, 3 m. So, 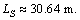 vmax is set as 10 m/s and amax is set as 2 m/s2. Figure 4 depicts the smooth trajectory and the initial positions of the individual in 3D space.
vmax is set as 10 m/s and amax is set as 2 m/s2. Figure 4 depicts the smooth trajectory and the initial positions of the individual in 3D space.

Figure 4 Smooth trajectory and initial position of individual
We run Algorithm 1 three times on an Intel(R) Core(TM) i5-2400 CPU @ 3.10 GHz with 4 GB internal memory. Three trajectory profiles are obtained which are illustrated in Figure 5. Based on these three trajectory profiles, velocity value |v(t)| and acceleration value |a(t)| of the individual corresponding to each profile are computed respectively, as illustrated in Figure 6.
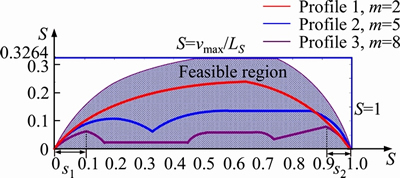
Figure 5 Three obtained trajectory profiles
By setting different m0, the cost time of Algorithm 1 is obtained in Figure 7. In Figure 8, two snapshots are shown. From Figure 7, the experiment results show that the velocity of the individual is continuous. The individual’s velocity and acceleration are constrained by the maximum velocity and acceleration, respectively. Moreover, from Figure 6(b), we can see that the individual’s acceleration changes with a frequent controlled by parameter m0 which increases the visual variety of the individual’s motion. Also this can be verified by Figure 8 and the videos in the supplementary materials.
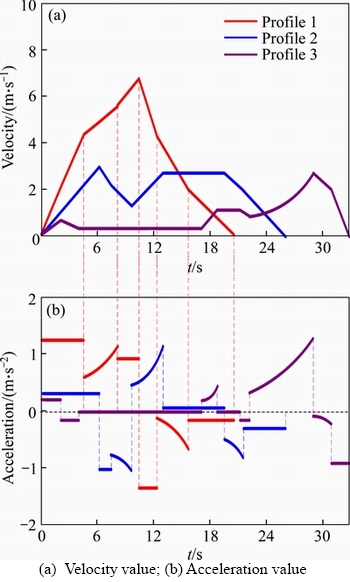
Figure 6 Velocity and acceleration value of individual corresponding to three trajectory profiles:
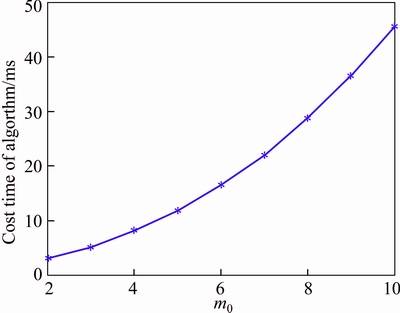
Figure 7 Cost time of Algorithm 1 according to different m0
In fact, other probabilistic sampling methods,such as RRT, can also construct roadmaps covering the free space. The disadvantage of the RRT method is that the tree structure generated by RRT consists of many short paths instead of long ones. The same number of sampling points will result in many small arcs in the smooth path roadmap. At these arcs, the virtual individual behaves as “sharp turn” behavior, which is not true if there are too many “sharp turns” in the whole virtual crowd movement. In addition, the RRT approach has poor efficiency in environments with amount of obstacles, especially narrow channels. The PRM method can avoid this situation by adopting appropriate sampling strategies (such as bridge-test to enhance sampling points in narrow channels). In addition, some improved RRT methods are also not suitable for this paper, because the design purpose of these methods is to find a path connecting the target points as soon as possible by controlling the growth direction of the random tree, so it is impossible to form a full coverage of free space.
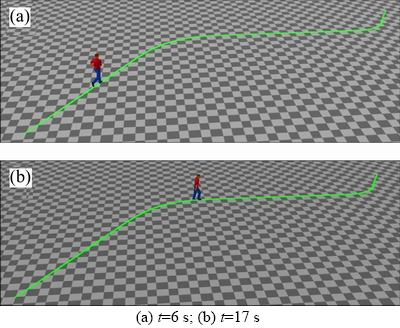
Figure 8 Snapshots when m0=8:
In order to verify the difference between the path roadmap produced by PRM and other sample based algorithms, e.g., RRT, we designed the following experiment. In a 20 m×20 m area, there are two equilateral right triangle obstacles (right-angle side 10 m) whose hypotenuse is parallel to the same diagonal of the square area. The two triangles are both 4 m away from the horizontal and vertical sides of the square. By this way, five narrow passages are built, four of which have parameters of 10 m×4 m and the other has 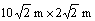 . Bridge test sampling strategy is adopted for PRM. Length threshold of small branch is set as 0.5 m which corresponds to the comfortable turning radius of pedestrians. The initial value of the RRT and RRT variant which determines whether the sampling point is the target point or the random point based on probability is set to the upper left of the area. The target point is set to the point at the extension line of the diagonal to ensure that RRT and RRT variant do not converge to get the specified number of sampling points.
. Bridge test sampling strategy is adopted for PRM. Length threshold of small branch is set as 0.5 m which corresponds to the comfortable turning radius of pedestrians. The initial value of the RRT and RRT variant which determines whether the sampling point is the target point or the random point based on probability is set to the upper left of the area. The target point is set to the point at the extension line of the diagonal to ensure that RRT and RRT variant do not converge to get the specified number of sampling points.
Figures 9 and 10 respectively depict the coverage of path points’ smallest enclosing polygon relative to experiment area and small branches of PRM versus RRT and RRT variant according to the number of sampling points.
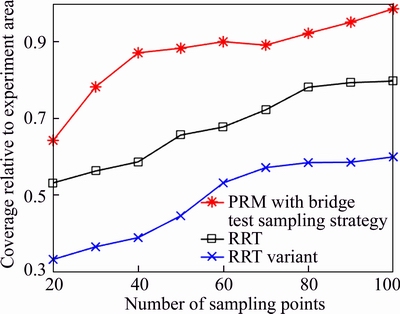
Figure 9 Coverage of PRM, RRT and RRT variant relative to experiment area according to number of sampling points
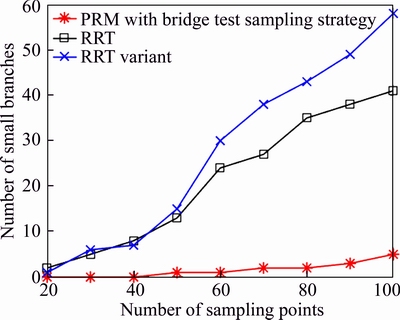
Figure 10 Number of small branches of PRM , RRT and RRT variant according to number of sampling points
Figures 9 and 10 indicate that compared with RRT and its variant algorithm, PRM algorithm generates fewer short branches which means fewer “sharp turns” and more realistic movements and has higher space coverage. All the above advantages lay the foundation for the work of this paper.
7 Conclusions
In this paper, we have presented a new approach to generate high-quality trajectory for heterogeneous individuals. In our approach, the individual’s path is smooth and the velocity is continuous. Simultaneously, the individual’s velocity and acceleration satisfy the physiological constraints of humans, i.e., dynamic constraints. Moreover, in order to increase the visual variety of a human’s locomotion, appropriate variation of velocity is considered in Algorithm 1. Therefore, the visual authenticities of individuals in a simulated crowd are greatly improved.
However, comfortable locomotion may conflict with m0 when m0 is set a big value. Therefore, future work may pay attention to the method which utilizes statistical information to select m0. In addition, it is worth reminding that our paper mainly aims the applications for low density crowd in open space. So, collision avoidance problem is not considered in this work. If we apply our method to crowded environment, collision avoidance behaviors must be added. Actually, our approach can be combined with existing collision avoidance methods, by the way that the velocity on the high-quality trajectory can serve as the preferred velocity in RVO method. So, this point is also the focus of our future work.
References
[1] XUE Zhu-xin, DONG Qing, FAN Xiang-tao, JIN Qing-wen, JIAN Hong-deng, LIU Jian. Fuzzy logic-based model that incorporates personality traits for heterogeneous pedestrians [J]. Symmetry-Basel, 2017, 9(10). DOI: 10.3390/ sym9100239.
[2] LE P T, HOANG H V, SANG H A, SEUNG G L, DONG H K, TAE C C. Univector field method-based multi-agent navigation for pursuit problem in obstacle environments [J]. Journal of Central South University, 2017, 24(4): 1002–1012. DOI: 10.1007/s11771-017-3502-0.
[3] XU Ming-liang, LI Chao-chao, LV Pei, CHEN Wei, DINESH M, DENG Zhi-gang, ZHOU Bing. Crowd simulation model integrating physiology-psychology-physics factors [J]. Computing Research Repository (CoRR), 2018, 18(1): 1–14. https://dblp.uni-trier.de/pers/hd/x/Xu:Mingliang, 2018-08-1/.
[4] BELLOMO N, CLARKE D, GIBELLI L, TOWNSEND P, VREUGDENHIL B J. Human behaviours in evacuation crowd dynamics: From modelling to big data toward crisis management [J]. Physics of Life Reviews, 2016, 18: 1–21. DOI: 10.1016/j.plrev.2016.05.014.
[5] CHOSET H M, HUTCHINSON S, LYNCH K M, KANTOR G, BURGARD W, KAVRAKI L E, THRUN S. Principles of robot motion: Theory, algorithms, and implementations [M]. MIT Press, 2005.
[6] NARANG S, BEST A, FENG A, KANG S H, MANOCHA D. Motion recognition of self and others on realistic 3D avatars [J]. Computer Animation and Virtual Worlds, 2017, 28(3, 4): e1762. DOI: 10.1002/cav.1762.
[7] KAPADIA M, PELECHANO N, ALLBECK J. Virtual crowds: Steps toward behavioral realism [M]. Synthesis Lectures on Visual Computing: Morgan & Claypool Publishers, 2015.
[8] LI Meng, LIANG Jia-hong, LI Shi-lei. Flocking behavior with multiple leaders and global trajectory [J]. Journal of Central South University, 2014, 21(6): 2324–2333. DOI: 10.1007/s11771-014-2184-0.
[9] WALLAR A, PLAKU E. Path planning for swarms by combining probabilistic roadmaps and potential fields [C]// 14th Annual Conference on Towards Autonomous Robotic Systems. Berlin, Heidelberg, 2013: 417–428. DOI: 10.1007/978-3-662-43645-5_43.
[10] LIU Qian. The effect of dedicated exit on the evacuation of heterogeneous pedestrians [J]. Physica A–Statistical Mechanics and Its Applications, 2018, 506: 305–323. DOI: 10.1016/j.physa.2018.04.032.
[11] CHARALAMBOUS P, CHRYSANTHOU Y. The PAG Crowd: A graph based approach for efficient data-driven crowd simulation [C]// Computer Graphics Forum, 2014, 33(8): 95–108. DOI: 10.1111/cgf.12403.
[12] KREMYZAS A, JAKLIN N, GERAERTS R. Towards social behavior in virtual-agent navigation [J]. Science China Information Sciences, 2016, 59(11): 1–17. DOI: 10.1007/s11432-016-0074-9.
[13] BEST A, NARANG S, CURTIS S, MANOCHA D. Densesense: Interactive crowd simulation using density- dependent filters [C]// Proceedings of the ACM SIGGRAPH/Eurographics Symposium on Computer Animation. Copenhagen, Denmark, 2014: 97–102. http://gamma.cs.unc.edu/DenseSense/,2018-08-1/.
[14] MARCELO K, MUBBASIR K. Geometric and discrete path planning for interactive virtual worlds [C]// ACM SIGGRAPH 2016: the 43rd International Conference and Exhibition on Computer Graphics & Interactive Techniques. Anaheim, CA, 2016. DOI: 10.1145/2897826.2927310.
[15] NORMAN J, ANGELOS K, ROLAND G. Adding sociality to virtual pedestrian groups [C]// Proceedings of the 21st ACM Symposium on Virtual Reality Software and Technology. Beijing, China, 2015: 163–172. DOI: 10.1145/2821592.282159.
[16] YAN Zhe-ping, LIU Yi-bo, YU Chang-bin, Zhou Jia-jia. Leader-following coordination of multiple UUVs formation under two independent topologies and time-varying delays [J]. Journal of Central South University, 2017, 24(2): 382–393. DOI: 10.1007/s11771-017-3440-x.
[17] MARBLE J D, BEKRIS K E. Asymptotically near-optimal is good enough for motion planning [J]. Robotics Research, 2017: 419–436. DOI:10.1007/978-3-319-29363-9_24.
[18] RAHMANI V, PELECHANO N. Improvements to hierarchical pathfinding for navigation meshes [C]// Proceedings of the Tenth International Conference on Motion in Games. Barcelona, Spain, 2017: 2–8. DOI: 10.1145/3136457.3136465.
[19] NINOMIYA K, KAPADIA M, SHOULSON A, GARCIA F, BADLER N. Planning approaches to constraint-aware navigation in dynamic environments [J]. Computer Animation and Virtual Worlds, 2015, 26(2): 119–139. DOI: 10.1002/cav.1622.
[20] AGARWAL P K, FOX K, SALZMAN O. An efficient algorithm for computing high-quality paths amid polygonal obstacles [J]. ACM Transactions on Algorithms (TALG), 2018, 14(4): 46–67. DOI: 10.1145/3230650.
[21] LINO C, CHRISTIE M. Intuitive and efficient camera control with the toric space [J]. ACM Transactions on Graphics, 2015, 34(4): 1–12. DOI: 10.1145/2766965.
[22] LI Bai, WANG Ke-xin, SHAO Zhi-jiang. Time-optimal maneuver planning in automatic parallel parking using a simultaneous dynamic optimization approach [J]. IEEE Transactions on Intelligent Transportation Systems, 2016, 17(11): 3263–3274. DOI: 10.1109/TITS.2016.2546386.
[23] LI Bai, LIU Hong, XIAO Duo, YU Gui-zhen, ZHANG You-min. Centralized and optimal motion planning for large-scale AGV systems: A generic approach [J]. Advances in Engineering Software, 2017, 106: 33–46. DOI: 10.1016/j.advengsoft.2017.01.002
[24] BROGAN D C, JOHNSON N L. Realistic human walking paths [C]// Proceedings of the 16th International Conference on IEEE Computer Animation and Social Agents, 2003: 94–101. DOI: 10.1109/CASA.2003.1199309.
[25] TOHFEH F, FAKHARIAN A. Polynomial based optimal trajectory planning and obstacle avoidance for an omni-directional robot [C]// Proceedings of the 5th Conference on Artificial Intelligence and Robotics, 2015: 53–59. DOI: 10.1109/RIOS.2015.7270731.
[26] BUTLER S D, MOLL M, KAVRAKI L E. A general algorithm for time-optimal trajectory generation subject to minimum and maximum constraints [C]// Proceedings of the Workshop on the Algorithmic Foundations of Robotics, 2016: 1–16. https://pdfs.semanticscholar.org/2875/f611c908e5bba 796a72ffb5cf349d96009bc.pdf, 2018-08-1/.
[27] BUTLER S D. General algorithms for the time-optimal trajectory generation problem [D]. Houston, USA: Rice University, 2017.
[28] CHEN Yu-xiao, PENG Huei, GRIZZLE J. Obstacle avoidance for low-speed autonomous vehicles with barrier function [J]. IEEE Transactions on Control Systems Technology, 2018, 26(1): 194–206. DOI: 10.1109/TCST. 2017.2654063 .
(Edited by FANG Jing-hua)
中文导读
针对异质群体的高质量轨迹规划方法
摘要:基于具有最大速度和最大加速度约束的轨迹规划方法,针对人群仿真中的异质群体,提出一种新颖的高质量轨迹规划方法。该方法能够保证个体的运动路径是平滑的,个体的速度是连续的。考虑到真实人具有最大速度和最大加速度的生理学约束,本文首先推导出一种时间最优的轨迹和可行域来解决kinodynamic规划问题。随后,通过计算具有恰当速度多样性的轨迹设计出一种高质量的轨迹规划方法。仿真结果表明提出的轨迹规划方法具有更高的真实性,能够为人群仿真中的虚拟人提供高质量的运动轨迹。
关键词:异质人群;轨迹规划;有界的速度和加速度;视觉多样性;真实性
Foundation item: Project(1708085QF158) supported by the Natural Science Foundation of Anhui Province, China
Received date: 2018-01-23; Accepted date: 2018-08-04
Corresponding author: LI Meng, PhD, Lecturer; Tel: +86-17756003093; E-mail: mengshuqin1984@163.com; ORCID: 0000-0002- 0126-2411

