DOI: 10.11817/j.issn.1672-7207.2017.10.017
基于改进Lorenz混沌系统的图像加密新算法
汪彦1, 2，涂立2
(1. 中南大学 软件学院，湖南 长沙，410083；
2. 湖南城市学院 信息与电子工程学院，湖南 益阳，413000)
摘要：为了提高图像加密算法的加密安全性和抗攻击能力，提出一种基于改进Lorenz混沌系统的图像加密新算法。首先，将Lorenz系统中的1个非线性项用指数函数项与单变量2次平方项的和替代；然后，分析该改进Lorenz系统的动力学特性，证实其混沌特性；最后，利用该混沌映射生成分别用于置乱加密和替代加密的2组密钥序列，进行图像的加密和解密操作：在置乱加密阶段，将图像像素灰度进行升序排列，并与置乱加密密钥序列结合实现像素位置置乱；在替代加密阶段，采用密文反馈的加密方式修改像素灰度。研究结果表明：该算法能有效抵御选择明文攻击，密文图像像素具有类随机均匀分布特性，且相邻像素具有零相关特性，拥有192 bit的密钥空间且对密钥非常敏感。
关键词：Lorenz系统；图像加密；混沌系统；置乱
中图分类号：TP309.7 文献标志码：A 文章编号：1672-7207(2017)10-2678-08
A new image encryption algorithm based on improved Lorenz chaotic system
WANG Yan1, 2, TU Li2
(1. School of Software,Central South University, Changsha 410083, China;
2. School of Information and Electronic Engineering, Hunan City University, Yiyang 413000, China)
Abstract: In order to improve the security and anti-attack ability of image encryption algorithm, a new image encryption algorithm based on improved Lorenz chaotic system was proposed. Firstly, a nonlinear term in the Lorenz system was replaced by an exponential function term and a two-square term of a single variable. Then, the dynamic characteristics of the improved Lorenz system were analyzed, which proved the chaotic characteristics of the system. Finally, the chaotic map was used to generate two groups of key sequences which were used for scrambling encryption and alternative encryption. In the scrambling encryption stage, the image pixel gray values were arranged in ascending order, and were combined with encryption key sequence to achieve pixel position scrambling. In the replacement encryption stage, the gray values of the pixels were modified by the way of cipher text feedback. The results show that the algorithm can effectively resist chosen plaintext attack, and the encrypted image has random-like distribution behavior of grey values and the adjacent pixels have zero correlation. The algorithm has 192 bit key spaces and it is very sensitive to the key.
Key words: Lorenz system; image encryption; chaotic system; scrambling
图像是人们获取信息的主要来源。相关统计结果表明，视觉提供了人们每天所感知信息的比例高达80%。图像是视觉信息的主要表现形式之一，具有形象、直观、生动的特点，在生活中得到了广泛应用。随着计算机网络技术和通信技术的迅猛发展，越来越多的数字图像需要在复杂多变的网络环境中处理、传输和存储，图像信息的安全性问题日益受到重视[1]。在很多应用场合，数字图像信息往往与个人隐私、商业秘密、军事情报甚至国家安全等密切相关，如何合理采用加密技术、切实保障这些信息不被非授权者非法窃取，是具有现实意义而不容忽视的重大问题。由于数字图像自身具有数据量大、相关性强以及冗余度高等特点，使得传统的密码学方法应用到图像加密场合效果并不理想[2]。由于混沌系统具有类随机性、遍历性和初值敏感性等特点，因此，将离散混沌系统运用于加密领域[3]，并提出了基于混沌的图像加密思想[4]。自此，研究者纷纷将图像加密与混沌联系起来。涂立等[5]提出了一种基于二维广义Logistic混沌映射的图像加密算法；YANG等[6]提出了一种基于混沌约瑟夫矩阵的图像加密算法；陈鸿等[7]采用混沌理论和小波变化，设计了图像加密压缩算法；邓晓衡等[8]针对加密算法存在的安全缺陷问题，提出了一种像素位置与比特双重置乱的图像混沌加密算法。采用一维的混沌系统对图像加密，存在安全性低、密钥空间小等问题，为此，邓晓衡等[8-14]采用高维Lorenz系统或改进Lorenz系统进行图像加密。为进一步提高安全性、扩大密钥空间、抵御选择明文攻击，本文作者提出一种基于改进Lorenz混沌系统的图像加密新算法。
1 混沌系统
所谓混沌[15]，就是指在确定性的非线性系统中出现的一种看似毫无规则、类似随机的独特现象，表现出对系统初值和控制参数的高度敏感性和类随机行为。混沌一般具有如下特征：初值敏感性；内随机性；遍历性。混沌的优良特性使其非常适合应用到密码学领域。下面介绍Lorenz混沌系统及其改进方法。
1.1 Lorenz系统
洛伦兹在研究对流实验的过程中发现了一个高维的动力学系统，这是世界上第1个表现奇异吸引子的连续动力学系统，同时表现出非常复杂的非线性动力学行为特征。该系统描述了从水桶底部加热时桶内液体的运动情况。这一系统被称为Lorenz系统[16]，其动力学方程如下：
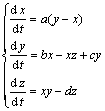(1)
其中：a，b，c和d为Lorenz系统参数，均可取大于0的任意实数，当取a=10，b=28，c=1，d=8/3时，Lorenz系统进入混沌状态。由上述Lorenz混沌系统得到的混沌序列在应用到信息加密场合时，存在宽频带特性较弱、序列相关性不够理想以及局部区域的单调性等问题，因此，有必要对Lorenz混沌系统加以改造，以便更加契合信息加密领域的实际需要。
1.2 Lorenz系统的改进方法
张成亮等[17]提出将Lorenz微分方程组的变量z的微分方程中的非线性项xy用指数函数exy替换。取系统参数a=10，b=40，c=1，d=2.5时，可得最大的Lyapunov指数LE1=1.733 0。而对于同样的参数设置，原始Lorenz系统(1)的最大Lyapunov指数L1=1.213 2。该改进系统比系统(1)具有更大的正的Lyapunov指数，这说明前者的混沌行为更复杂，根据前者得到的混沌系列更适宜于信息加密。
官国荣等[12]提出用x2来替代exy。当给定系统参数a=10，b=40，c=1，d=2.5时，最大的Lyapunov指数L1=2.060 6，这说明该改进系统得到了更大的正的Lyapunov指数，其混沌动力学行为表现更复杂。
2 新的改进Lorenz系统及其动力学特性分析
2.1 一种新的改进Lorenz系统
在对原Lorenz系统分析的基础上，构建如下改进Lorenz混沌系统：
(2)
对于上述系统，取参数a=10，b=40，c=1，d=2.5时，可得最大的Lyapunov指数L1=2.084 0，L2=0，L3=-13.597 0。这说明系统(2)相比原始Lorenz系统以及张成亮等[17]提出的改进系统得到了更大的正Lyapunov指数，其混沌行为表现更加复杂。通过反复实验发现，对于系统(2)的第3个方程，平方项系数设置为200，指数函数项系数设置为0.01，此时，系统(2)具有更加复杂的混沌行为。
2.2 改进Lorenz系统的动力学特性分析
对于改进Lorenz系统(2)，有必要从混沌系统动力学角度出发，对该系统的动力学性质进行深入探究。
2.2.1 改进Lorenz混沌系统的混沌吸引子的相位图
对于系统(2)，给定系统参数a=10，b=40，c=1，d=2.5时，采用Matlab7.1绘制该混沌系统的混沌吸引子的相位图，如图1所示。
由图1可知：改进的Lorenz混沌系统(2)的混沌吸引子的拉伸轨线和折叠轨线非常复杂，呈现出混沌特征。
2.2.2 系统的对称性分析
系统(2)在变换F:(x，y，z)→(-x，-y，z)下保持不变，这说明系统(2)关于Z轴对称。
2.2.3 耗散性即混沌吸引子的存在性
因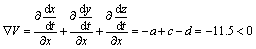
，故改进Lorenz系统(2)是耗散的，系统的状态变化有界，并且以指数速率
收敛到0。这说明系统(2)的吸引子存在。
2.2.4 平衡点与稳定性分析
在系统(4)中，令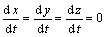
，即可得以下三元二次方程组：
(3)
将系统参数a=10，b=40，c=1，d=2.5代入式(3)，即可得到系统(2)的3个平衡点：S1(0，0，0.004 0)，S2(-0.715 8，-0.715 8，41.000 0)，S3(0.715 8，0.7158，41.000)。
现将系统(2)线性化，可得到其Jacobian矩阵：
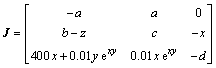(4)
将点S1(0，0，0.004 0)代入式(4)，根据Jacobian矩阵可解出3个特征根：λ1=25.241 5，λ2=16.241 5，λ3=-2.500 0。这些特征根中既有正值也有负值，据Routh-Hurwitz条件，可知点S1是不稳定鞍结点。同样地，分别将点S2(-0.715 8，-0.715 8，41.000 0)和S3(0.715 8，0.715 8，41.000 0)代入式(4)，可得到3个特征根：λ1=-17.153 6，λ2=2.862 8+10.559 2i，λ3=2.862 8-10.559 2i。其中，i为虚数单位；λ1为负实根，λ2和λ3则为1对具有正实部的共轭复根，据此可判定S2和S3均为系统的不稳定鞍结点。
图1 系统(2)混沌吸引子的平面投影与相位图
Fig. 1 Plane projections and phase diagram attractors of system (2)
2.2.5 Lyapunov指数与维数分析
混沌的一个非常重要的特点是初始状态的细微不确定性以指数速度快速扩大，这种轨迹发散或者收敛的比率可用Lyapunov指数定量刻画。利用Jacobian矩阵可计算动力系统的Lyapunov指数。给定系统参数a=10，b=40，c=1，d=2.5，并确定初值为(3，3，3)，计算系统(2)的3个Lyapunov指数,依次用L1，L2和L3表示，随时间变化的曲线如图2所示，其中L1=2.084 0，L2=0，L3=-13.597 0。
图2 系统(2)的Lyapunov指数
Fig. 2 Lyapunov index of system (2)
根据求得的Lyapunov指数，可按下式计算系统(2)的Lyapunov维数为
(5)
可求出dL=2.153 0。由此可见，系统(2)有1个Lyapunov指数是正值，而其Lyapunov维数是分数，故系统(2)是混沌系统。
3 图像加密算法基本原理
本文提出的图像加密算法利用提出的改进Lorenz系统生成用于加解密的混沌序列流，下面分别介绍加密过程和解密过程。
3.1 图像加密过程
本文提出的图像加密算法属于典型的置乱—替代结构的混沌加密方案。这种方案一般先利用混沌映射对图像像素位置进行置乱，然后利用混沌映射对图像像素替代加密。
3.1.1 基于图像像素位置的置乱加密
所谓像素位置的置乱，指按照某种方式将图像的各个像素的位置在全图范围内进行改变，以降低甚至消除图像中相邻像素之间的相关性，从而增强图像加密的安全性。图像像素的置乱加密算法具体步骤如下。
Step 1：将明文图像对应的二维矩阵Am×n按照行优先的方式进行转换，拉伸成一维的像素灰度序列
。
Step 2：输入密钥，即改进Lorenz混沌系统(2)的初始值x0，y0和z0，迭代式(2) m×n次，产生混沌序列流
(其中，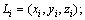
)。
Step 3：利用混沌序列L和式(6)构造置乱初始序列
。
(6)
式中：xi和yi为Li的2个分量；i=1，2，3，…，m×n。
Step 4：将明文图像的灰度序列
由小到大排序，产生有序序列
。
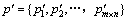Step 5：利用序列R和像素值有序序列p′，生成用于置乱加密的序列
，其中元素
由下式确定：
(7)
Step 6：将序列Q从小到大排列，得到新的有序序列，并生成用于依次记录该新序列中各元素在原序列Q中位置的新序列
。
Step 7：利用序列T对明文图像的像素灰度序列进行置乱，得到置乱图像的像素值序列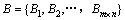
，其中元素Bi由下式确定：
(8)
3.1.2 基于异或运算的像素替代加密
像素替代加密阶段主要完成对置乱图像像素序列B的元素的替代加密，以改变加密图像的直方图，进一步混淆密文图像与明文图像之间的关系，增强算法的安全性。基于异或运算的图像像素替代加密的具体操作步骤如下。
Step 1：利用图像像素置乱加密阶段Step 2生成的混沌序列L和下式构造替代初始序列
：
(9)
式中：yi和zi为Li的2个分量；
。
Step 2：将序列W的元素Wi的小数点后的第2，4和6位取出组成1个3位的整数，然后对256进行整除求余，这样将实数序列W改造成用于替代加密的整数序列
。
Step 3： 设最终密文图像的像素序列为
，按照下式构造该序列：
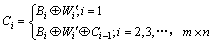(10)
式中：
表示对前、后的2个整数进行按位异或运算。需要指出的是，在采用循环构造最终密文图像的像素序列时，应该按照下标从小到大的顺序依次进行。
Step 4：将一维的最终密文图像的像素序列转换为二维m×n的矩阵，得到最终的密文图像。至此，整个加密算法结束。
3.2 图像解密过程
图像的解密过程是加密的逆过程。加密算法分为像素置乱加密与像素替代加密这2个按先后顺序依次进行的过程。图像解密同样包含2个过程，即图像替代解密和像素置乱解密。需注意的是，需要先进行图像替代解密操作，然后进行像素置乱解密操作。图像解密具体过程如下。
Step 1：将密文图像像素灰度矩阵拉伸成一维的像素序列，结合采用与加密过程中相同的方法产生的序列W′，按照式(11)计算图像像素置乱序列。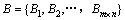
(11)
Step 2：进行图像像素置乱的解密操作。这一操作与图像置乱加密操作过程大体一致，又略有不同，其目标是由图像像素置乱序列B还原出明文图像的像素序列p。采用与像素位置置乱加密相同的方法构造序列流Q。值得注意的是，由于置乱像素序列B和明文像素序列p包含的像素元素能够一一对应，只是顺序不一致而已，将两者分别从小到大排列得到的像素值有序序列是完全一样的，不妨仍然记作p′。这样，利用Q和p′，可以得到用于反置换的Q′，将Q′按从小到大的顺序排序，进一步得到新序列。最后，利用式(12)还原出明文图像的像素序列p，将其转换成二维的m×n的矩阵，就得到解密后的明文图像。
(12)
4 仿真实验效果
在算法的仿真实验过程中，选择经典的分辨率为256×256的8位灰度图像作为实验对象，在Win7平台上利用Matlab7.1进行仿真实验，混沌映射的初值和参数设置为：x0=0.12，y0=0.23，z0=0.34，a=10，b=40，c=1，d=2.5。由实验采用的原始图像和仿真实验得到的加密图像如图3所示。由图3(b)可以观察到：凭借肉眼来判别，加密图像中已看不到任何有用信息，也无法直接获取加密图像与原始图像之间的关联。
图3 原始图像和加密图像
Fig. 3 Original image and encrypted image
5 算法性能分析
5.1 直方图分析
灰度直方图是灰度级的函数，描述的是图像中各灰度级具有的像素个数，直观地体现了灰度图像中像素的分布特性。图4所示为原始明文图像和加密图像的灰度直方图。原始图像的像素灰度分布极不均匀，而加密图像的像素灰度在[0，255]的区间较均匀分布。这说明加密算法完全改变了图像像素灰度的统计特性，使得密文图像能够抵御统计攻击。
5.2 信息熵分析
热力学中用熵来表示物理系统的无序性。SHANNON于1948年将熵的概念与信息论结合起来，提出了信息熵[18]的概念。现假设随机变量
，p(xi)表示xi出现的概率，那么，X的信息熵H(X)可用下式表示：
(13)
图4 原始图像的灰度直方图和加密图像的灰度直方图
Fig. 4 Histogram of original image and Histogram of encrypted image
p(xi)需要满足下式给定条件：
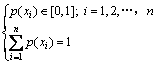(14)
对于1幅256级灰度图像，xi表示像素的灰度，只能取0~255之间的256个整数。当图像中各灰度出现的概率相等，即
时，代入式(13)，可求得该图像的信息熵为8，这是256级灰度图像信息熵的最大值。图像的信息熵客观地反映了图像中各灰度值分布的均匀程度，熵越大，则图像的灰度分布越均匀。原始明文图像采用本加密算法处理后，得到的密文图像信息熵为7.990 1，接近理想值8.000 0，说明本加密算法具有良好的效果，是安全的。
5.3 图像相邻像素的相关性分析
通常，原始图像中的像素之间是彼此相关的，尤其是相邻像素之间具有高度的相关性。图像加密算法的目标之一就是尽可能降低密文图像的相邻像素之间的相关性。在某数字图像中随机选取n个像素，它们的灰度组成1个灰度序列，记作
，其灰度的均值记作EX，即
。这n个像素都具有对应的相邻像素，将这些相邻像素的灰度组成的序列记作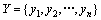
。同样有
。将ρXY定义为这2组相邻像素之间的相关系数，可按下式计算[19]：
(15)
针对图3所示的原始图像和加密图像，分别在水平、垂直、对角这3个方向上，各自随机挑选1 000组邻点，计算它们的相关系数。仿真实验结果如表1所示。
表1 原图和密图的相邻像素的相关系数
Table 1 Correlation coefficient of adjacent pixels for original image and encrypted image
由表1可知：原始图像的相邻像素之间的相关系数绝对值都超过了0.900 0，相邻像素是高度相关的。而加密图像的相关系数的绝对值都小于0.010 0。这说明提出的加密算法破坏了原始图像中相邻像素的相关性，密文图像的像素分布具有良好的随机性。
5.4 密钥敏感性测试
对于加密算法而言，只有使用正确的密钥才能正确解密得到原始明文图像。对正确密钥进行微小改变，得到的解密图像与原始图像差别很大，无法从解密图像中获取有意义的原始图像相关信息，这种特性即为加密算法的密钥敏感性[20]。下面分别采用正确的密钥参数和不同的错误密钥参数对加密图像进行解密实验，以检验所提出算法的密钥敏感性。
首先，采用正确的密钥参数x1=0.12，y1=0.23，z1=0.34，所得到的解密图像如图5(a)所示。该图像与图3(a)所示原始图像是一致的，这说明采用正确的密钥参数能够成功地将密文图像恢复成明文图像。然后，依次将x1，y1和z1这3个参数的其中1个参数增加10-10，同时其余2个参数取正确的密钥参数，先后进行3次解密实验，得到的错误解密图像分别如图5(b)，(c)和(d)所示。从图5可见：即便只对密钥参数进行细微改变，得到的解密图像呈现类似于噪声的分布状态，与明文图像区别很大。
图5 解密图像
Fig. 5 Decrypted images
为了进一步准确地定量表达解密图像与明文图像之间的差异，引入图像灰度的均方差[4]这一概念。设P={pi,j}表示原始图像的像素灰度矩阵，P′={p′i,j}表示解密图像的像素灰度矩阵，原始图像和解密图像的分辨率均为m×n(其中，i=1，2，3，…，m；j=1，2，3，…，n)，则2幅图之间的灰度均方差
可由下式表示：
(16)
在仿真实验中，采用的明文图像和利用不同密钥得到的解密图像之间的灰度均方差如表2所示。从图6和表2可知：只有使用正确的密钥，才能通过解密还原出明文图像；即使密钥中的3个参数中某个参数发生微小变化，解密得到的图像也无法分辨出有意义的内容，且解密图像与明文图像之间的像素灰度均方差都在15 000以上，两者差别很大。这说明提出的加密算法对密钥中的3个参数均非常敏感。
表2 P与P′的均方差
Table 2 Mean square error of P and P′
5.5 密钥空间分析
算法的密钥空间是否足够大，能否抵抗攻击者的穷举攻击，是评判加密算法优劣的一个重要方面。本文提出的图像加密算法基于改进的Lorenz混沌系统，其密钥牵涉到x0，y0和z0这3个双精度参数。若双精度类型数据在计算机中为64 bit，那么，提出的加密算法密钥空间为264×264×264=2192。若将改进Lorenz混沌系统的参数a，b，c和d也作为密钥参数，则密钥空间更大。因此，本加密算法的密钥空间足够大，能够有效地防范穷举攻击。
6 结论
1) 提出一种新的改进Lorenz混沌系统。将Lorenz系统中的1个非线性项用指数函数项与单变量2次平方项的和替代，其能产生更复杂的混沌吸引子，具有更大的正Lyapunov指数。这说明改进的Lorenz混沌系统具有更好的混沌特性，有利于改善基于该改进Lorenz混沌系统的图像加密算法性能指标。
2) 提出一种有效抵御选择明文攻击的图像置乱加密方法。在由改进Lorenz混沌系统构造用于置乱的序列流后，将图像的灰度序列进行升序排列，然后将图像灰度升序序列与置乱序列流的对应元素相乘，利用得到的新序列进行置乱加密。这种置乱加密方法与明文图像的内容紧密相关，能有效抵御选择明文攻击。
3) 在图像像素替代加密阶段引入密文输出反馈机制，即将前一像素的加密结果作为加密密钥参与下一个像素的替代加密，强化了密文扩散效应，使得算法能够抵御差分攻击。
参考文献：
[1] 王永, 李昌兵, 何波. 混沌加密算法与Hash函数构造研究[M]. 北京: 电子工业出版社, 2011: 94-119.
WANG Yong, LI Changbing, HE Bo. Research on chaotic encryption algorithm and construction of hash function[M]. Beijing: Electronic Industry Press, 2001: 94-119.
[2] 向滔. 基于混沌的数字图像加密算法的分析与设计[D]. 重庆: 重庆大学计算机学院, 2014: 1-2.
XIANG Tao. Analysis and designs of digital image encryption algorithm based on chaos[D]. Chongqing: Chongqing University. School of Computer Science, 2014: 1-2.
[3] FU Chong, CHENG Junjie, ZOU Hao, et al. A chaos-based digital image encryption scheme with an improved diffusion strategy[J]. Optics Express, 2012, 20(3): 2363-2378.
[4] 朱铖. 基于混沌理论与小波变换的图像加密方法研究[D]. 上海: 东华大学信息科学与技术学院, 2013: 7-9.
ZHU Cheng. Image encryption method research based on chaos theory and wavelet transformation[D]. Shanghai: Donghua University. College of Information Science and Technology, 2013: 7-9.
[5] 涂立, 张弛, 贾丽媛. 基于二维广义Logistic映射的图像加密算法[J]. 控制工程, 2014, 21(2): 279-282.
TU Li, ZHANG Chi, JIA Liyuan. A novel image encryption algorithm based on two-dimensional generalized Logistic mapping[J]. Control Engineering of China, 2014, 21(2): 279-282.
[6] YANG Gelan, JIN Huixia, BAI Na. Image encryption using the chaotic Josephus matrix[J]. Mathematical Problems in Engineering, 2014(3): 632060-632072.
[7] 陈鸿, 柏森, 刘博文. 混沌和小波变换的图像加密压缩算法[J]. 重庆大学学报(自然科学版), 2014, 37(6): 65-70.
CHENG Hong, BAI Sen, LIU Bowen. An image encryption and compression algorithm based on chaos system and wavelet transform[J]. Journal of Chongqing University (Natural Science Edition), 2014, 37(6): 65-70.
[8] 邓晓衡, 廖春龙, 朱从旭, 等. 像素位置与 bit双重置乱的图像混沌加密算法[J]. 通信学报, 2014, 35(3): 216-223.
DEND Xiaoheng, LIAO Chunlong, ZHU Congxu, et al. Image encryption algorithm based on chaos through dual scrambling of pixel poison and bit[J]. Journal of Communication, 2014, 35(3): 216-223.
[9] 宋鑫超, 苏庆堂, 赵永升. 内联时延混沌映射耦合Lorenz系统的图像加密算法[J]. 计算机工程与设计, 2016, 37(7): 1757-1761.
SONG Xinchao, SU Qingtang, ZHAO Yongsheng. Image encryption algorithm based on inline time delay chaotic map coupled with Lorenz system[J]. Computer Engineering and Design, 2016, 37(7): 1757-1761.
[10] 祁燕, 刘丽萍. 标准映射和Lorenz混沌系统彩色图像加密算法[J]. 沈阳理工大学学报, 2014, 33(4): 40-47.
QI Yan, LIU Liping. Color image encryption algorithm based on standard and Lorenz chaos system[J]. Journal of Shenyang Ligong University, 2014, 33(4): 40-47.
[11] 谢国波, 苏本卉. 一种新的基于混沌的彩色图像加密算法[J]. 计算机应用与软件, 2016, 33(9): 324-327.
XIE Guobo, SU Benhui. A new chaotic-based color image encryption algorithm[J]. Computer Applications and Software, 2016, 33(9): 324-327.
[12] 官国荣, 吴成茂, 贾倩. 一种改进Lorenz混沌系统构造及其加密应用[J]. 小型微型计算机系统, 2015, 36(4): 830-835.
GUAN Guorong, WU Chengmao, JIA Qian. Application of an improved Lorenz chaotic system and in image encryption[J]. Journal of Chinese Computer Systems, 2015, 36(4): 830-835.
[13] 章秀君, 吴志强, 方正. 一种基于四维超混沌系统的数字图像加密算法[J]. 计算机工程, 2013, 39(8): 169-172.
ZHANG Xiujun, WU Zhiqiang, FANG Zheng. A digital image encryption algorithm based on four-dimensional hyperchaotic system[J]. Computer Engineering, 2013, 39(8): 169-172.
[14] 徐光宪, 郭晓娟. 基于混沌系统和DNA序列运算的新型图像加密[J]. 计算机应用研究, 2015, 32(6): 1766-1769.
XU Guangxian, GUO Xiaojuan. Novel images encryption algorithm based on chaotic system and DNA sequence operation[J]. Application Research of Computers, 2015, 32(6): 1766-1769.
[15] 朱和贵. 信息安全中混沌图像加密算法及其相关问题研究[D]. 吉林:吉林大学数学研究所, 2014: 5-9.
ZHU Hegui. The research of chaotic image encryption schemes and related problem in information security[D]. Jilin: Jilin University.Institute of Mathematics, 2014: 5-9.
[16] 肖潇, 胡春强, 邓邵江. 一种基于混沌的图像hash算法[J]. 计算机应用研究, 2011, 28(5): 1904-1905.
XIAO Xiao, HU Chunqiang, DENG Shaojiang. Image hash algorighm based on chaos theory[J]. Application Research of Computers, 2011, 28(5): 1904-1905.
[17] 张成亮, 王树斌, 王忠林. 一个含指数函数的混沌系统设计与电路实现[J]. 济南大学学报(自然科学版), 2013, 27(2): 140-144.
ZHANG Chengliang, WANG Shubin, WANG Zhonglin. Design and realization of a chaotic system with exponential function[J]. Journal of University of Jinan (Science & Technology), 2013, 41(3): 8-14.
[18] 晋建秀, 郑宜峰, 李叙琼. 基于分块信息熵方差的图像置乱程度评估[J]. 华南理工大学学报(自然科学版), 2013, 41(3): 8-14.
JIN Jianxiu, ZHENG Yifeng, LI Xuqiong. Evaluation of image scrambling degree base on block information entropy variance[J]. Journal of South China University of Technology (Natural Science Edition), 2013, 41(3): 8-14.
[19] 王静. 混沌数字图像加密技术研究[D]. 南京: 南京邮电大学自动化学院, 2013: 46-48.
WANG Jing. Study on chaotic digital image encryption[D]. Nanjing: Nanjing University of Posts and Telecommunications. College of Automation, 2013: 46-48.
[20] 朱从旭, 胡玉平, 孙克辉. 基于超混沌系统和密文交错扩散的图像加密新算法[J]. 电子与信息学报, 2012, 34(7): 1735-1743.
ZHU Congxu, HU Yuping, SUN Kehui. New image encryption algorithm based on hyperchaotic system and ciphertext diffusion in crisscross pattern[J]. Journal of Electronics and Information Technology, 2012, 34(7): 1735-1743.
(编辑 陈灿华)
收稿日期：2016-08-20；修回日期：2016-10-25
基金项目(Foundation item)：湖南省教育厅科研项目(17C0296)；益阳市指导性科技计划项目(20165111)(Project(17C0296) supported by the Scientific Research of Department of Education of Hunan Province; Project(20165111) supported by the Guiding Science and Technology Planning of Yiyang City, Hunan Province)
通信作者：汪彦，讲师，从事智能信息处理、数字图像处理等研究；E-mail：shaoguanzai@sina.com
