
Calculation of Cu-rich part of Cu-Ni-Si phase diagram
LU De-ping(陆德平)1, WANG Jun(王俊)2, A. Atrens3, ZOU Xing-quan(邹兴权)1,
LU Lei(陆磊)1 , SUN Bao-de(孙宝德)2
1. Institute of Applied Physics, Jiangxi Academy of Sciences, Nanchang 330029, China;
2. State Key Laboratory of Metal Matrix Composite, Shanghai Jiao Tong University, Shanghai 200030, China;
3. Division of Materials, The University of Queensland, Brisbane, Qld, Australia 4072
Received 15 July 2007; accepted 10 September 2007
Abstract: The thermodynamic calculation of phase equilibria in the Cu-Ni-Si alloy system was carried out using the CALPHAD method. The calculations show that there are three two-phase areas and two three-phase areas in the Cu-rich parts of the isothermal section of the phase diagram at 300-600 ℃, and the three two-phase areas are FCC-A1(Cu-rich)+γ-Ni5Si2, FCC-A1(Cu-rich)+δ-Ni2Si and FCC-A1(Cu-rich)+ε-Ni3Si2, two three-phase areas are FCC-A1(Cu-rich)+γ-Ni5Si2+δ-Ni2Si and FCC-A1(Cu-rich)+δ-Ni2Si+ε-Ni3Si2. For this reason, an alloy located in the Cu-rich portion may precipitate γ-Ni5Si2, δ-Ni2Si or ε-Ni3Si2; the proportion of each phase depends on the alloy composition and aging temperature. The transmission electron microscope analysis of the Cu-3.2Ni-0.75Si alloy indicates that the precipitates are mainly δ-Ni2Si with only a few γ-Ni5Si2 phase particles, which agrees well with the thermodynamic calculations of phase equilibria.
Key words: Cu-Ni-Si alloy; phase diagram calculation; thermodynamics
1 Introduction
Cu-Ni-Si alloys are widely used for the lead frames owing to their excellent strength and electrical conductivity[1-4]. Many alloys with different compositions have been developed. However, the design of these Cu-Ni-Si alloys mainly depended on trial and error. Furthermore the structure of precipitates in Cu-Ni-Si alloys is still controversial. LOOCKYER and NOBLE[5] reported that the structure of precipitates was similar to γ-Ni5Si2, whilst FUJIWARA[6] considered that the precipitates were β-Ni3Si. Many researchers believed that the precipitates are δ-Ni2Si and that some orientation relationship existed between the precipitates and the Cu matrix[7]. The structures and quantities of precipitates greatly influence the properties of the alloy, which mainly depend on the alloy composition and aging temperature. Therefore the scientific and reasonable design of alloy composition should be based upon the knowledge of the phase diagram.
In this paper, the thermodynamic calculation of phase equilibria in the Cu-Ni-Si alloy system is carried out by the CALPHAD method, and the structure and proportion of various precipitates are simulated at different aging temperature in Cu-3.2%Ni-0.75%Si. The results can act as guidelines for the design of high-strength and high-conductivity Cu-Ni-Si alloys.
2 Experimental
The isothermal sections of the Cu-rich part of the Cu-Ni-Si phase diagram were calculated using the Thermo-Calc software. Thermodynamic parameter optimization was carried out in the PARROT module of the Thermo-Calc software. This research used thermodynamic results of the Cu-Ni, Cu-Si and Ni-Si binary systems and thermodynamic parameters of the Cu-matrix thermodynamic database assessed by WANG et al[8].
The experimental alloy of composition Cu-3.2%Ni- 0.75%Si (designated Cu-3.2Ni-0.75Si) was melted and cast into ingots in a vacuum induction furnace. The ingots were hot rolled and cold rolled. The samples for microscopic analysis were cut from cold rolled bars. The samples were solution treated at 900 ℃ for 70 min in a furnace under nitrogen atmosphere, water quenched and then aged at 500 ℃ for 60 min.
The microstructures were examined with a JEM-2000EX transmission electron microscope. The samples were cut into discs and ground to a thickness of 0.3 mm, thinned to 60-80 μm by electro-polishing in 30 mL HNO3+10 mL H4PO3+50 mL CH3COOH at a voltage of 3 V for 3-4 min, electropolished using a twin jet electropolisher in 40%(volume fraction) H4PO3 in water below -10 ℃ and thinned with a Gatan 600 Duo-mill (DUAL10N Mill/gatan model 600).
3 Thermodynamic models
The Cu-Ni-Si ternary system contains solid solution phases (liquid phase, face-centered cubic (FCC) phase, body-centered cubic (BCC) phase, hexagonal close- packed (HCP) phase), and some intermediate phases. Although ternary compound phases in the Cu-Ni-Si system were reported by some researches[9], these phases have not been confirmed; therefore ternary compound phases are not to be considered in this paper.
The Gibbs free energy of the pure component i in the Φ phase can be expressed as:
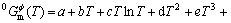
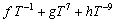 (1)
(1)
The data of pure components are taken from the SGTE(Scientific Group Thermodata Europe) database [10].
3.1 Liquid phase, fcc, bcc and hcp solid solution phases
The Gibbs free energy of the liquid, face-centered-cubic (FCC), body-centered-cubic (BCC), and hexagonal-close-packed (HCP) solid solution phases are described by the regular solution model:
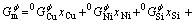


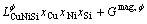 (2)
(2)
where 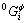 is the Gibbs free energy of pure component i in the respective reference state, xi is the molar fraction of component i, and
is the Gibbs free energy of pure component i in the respective reference state, xi is the molar fraction of component i, and 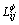 and
and  are the temperature and composition dependent interaction energy in the binary and ternary systems, respectively.
are the temperature and composition dependent interaction energy in the binary and ternary systems, respectively. 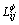 is the interaction parameter between i and j atoms.
is the interaction parameter between i and j atoms.  is the ternary interaction parameter. The concentration and temperature dependence of the parameters
is the ternary interaction parameter. The concentration and temperature dependence of the parameters 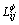 and
and  are expressed as follows:
are expressed as follows:

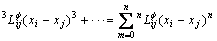 (3)
(3)
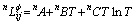 (4)
(4)
 (5)
(5)
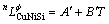 (6)
(6)
where A, B and C are thermodynamic parameters to be optimized.
 is the magnetic contribution to the Gibbs free energy, which can be calculated using the following formula:
is the magnetic contribution to the Gibbs free energy, which can be calculated using the following formula:
 (7)
(7)
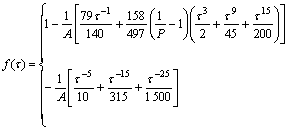 τ<1(8)
τ<1(8)
where  ;
; 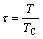 ; p is a constant, p=0.28 (for FCC alloy) or 0.40 (for BCC alloy).
; p is a constant, p=0.28 (for FCC alloy) or 0.40 (for BCC alloy).
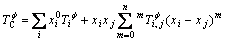 (9)
(9)
 (10)
(10)
where  is the critical temperature of magnetic order, which is the Curie temperature (TC) for ferromagnetic ordering and the Neel temperature (TN) for antiferromagnetic ordering;
is the critical temperature of magnetic order, which is the Curie temperature (TC) for ferromagnetic ordering and the Neel temperature (TN) for antiferromagnetic ordering;  is the Bohr magnetic moment.
is the Bohr magnetic moment. 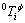 and
and  are magnetic data of pure component i;
are magnetic data of pure component i; 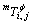 and
and  are magnetic interaction parameters between the i and j components.
are magnetic interaction parameters between the i and j components.
3.2 Linear compounds
The thermodynamic model treatment of linear compounds accords with the sublattice model. The general formula is ApBq, where p and q represent the mole number in the A and B sublattices. The Gibbs free energy of one mole of ApBq compound can be expressed as follows:
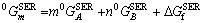 (11)
(11)
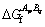 is the free energy of one mole of the ApBq compound, which can be written as
is the free energy of one mole of the ApBq compound, which can be written as
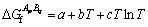 (12)
(12)
where a, b and c are thermodynamic parameters to be optimized.
4 Results and discussion
4.1 Isothermal sections of phase diagram
The calculated isothermal sections of the Cu-Ni-Si phase diagram in the Cu-rich part at 300, 400, 500 and 600 ℃ are presented in Fig.1(a)-(d). Fig.1 indicates that there are three two-phase areas and two three-phase areas in the Cu-rich part of the isothermal sections at 300-500 ℃. The three two-phase areas are FCC-A1(Cu-rich)+ γ-Ni5Si2, FCC-A1(Cu-rich)+δ-Ni2Si and FCC-A1(Cu- rich)+ε-Ni3Si2. The two three-phase areas are FCC- A1(Cu-rich)+γ-Ni5Si2+δ-Ni2Si and FCC-A1(Cu-rich)+δ- Ni2Si+ε-Ni3Si2. There are two two-phase areas, FCC- A1(Cu-rich)+γ-Ni5Si2 and FCC-A1(Cu-rich)+δ-Ni2Si, one three-phase area, FCC-A1(Cu-rich)+δ(Ni2Si)+ γ(Ni5Si2), and one single-phase area FCC-A1(Cu-rich) at 600 ℃. According to the phase diagram, an alloy located in the Cu-rich part may precipitate γ-Ni5Si2, δ-Ni2Si or ε-Ni3Si2; the proportion of each phase depends on the alloy composition and aging temperature. This is the reason why there are different reports in the literature concerning the structure of precipitates in the Cu-Ni-Si system.
4.2 Structure and mass fraction of phases of experimental alloy in equilibrium state
The structure and mass fraction of phases of the Cu-3.2Ni-0.75Si experimental alloy were calculated in the equilibrium state. The results are shown in Fig.2. The isothermal sections of the phase diagram in Fig.1 show that the alloy Cu-3.2Ni-0.75Si is located at the boundary of the FCC-A1(Cu-rich)+γ-Ni5Si2+δ-Ni2Si three-phase area and the FCC-A1(Cu-rich)+δ-Ni2Si two-phase area at 300, 400, 500 and 600 ℃. Therefore, the δ-Ni2Si phase and the γ-Ni5Si2 phase will precipitate in this alloy during aging. Fig.2 indicates that with decreasing temperature the mass fraction of δ-Ni2Si phase will increase, whilst the mass fraction of γ-Ni5Si2 will decrease.

Fig.1 Calculated Cu-rich isothermal section of Cu-Ni-Si phase diagram at 300 ℃ (a), 400 ℃ (b), 500 ℃ (c) and 600 ℃ (d)
4.3 TEM evaluation of precipitates
The morphology of precipitates in the Cu-3.2Ni- 0.75Si alloy aged at 500 ℃ is shown in Fig.3. The disc-like precipitates are distributed uniformly in the matrix with a diameter of about 30 nm. The diffraction pattern of the precipitates confirms that the precipitates have an orthorhombic lattice similar to δ-Ni2Si.
In the TEM image of the precipitates, a few disc-like precipitations with a diameter of about 60 nm (Fig.4) are also found. The results of the diffraction pattern indicate that the precipitates are γ-Ni5Si2 phase. The experiment results show that the precipitates are mainly δ-Ni2Si phases and there are only a few γ-Ni5Si2 phases, which agrees well with the thermodynamic calculation results of phase equilibria.

Fig.2 Mass fraction of phases of Cu-3.2Ni-0.75Si alloy in equilibrium state

Fig.3 TEM image of δ-Ni2Si precipitates in Cu-3.2Ni-0.75Si alloy aged at 500 ℃

Fig.4 TEM image of γ-Ni5Si2 precipitate in Cu-3.2Ni-0.75Si alloy aged at 500 ℃
4 Conclusions
1) There are three two-phase areas, FCC- A1(Cu-rich)+γ-Ni5Si2, FCC-A1(Cu-rich)+δ-Ni2Si and FCC-A1(Cu-rich)+ε-Ni3Si2, and two three-phase areas, FCC-A1(Cu-rich)+γ-Ni5Si2+δ-Ni2Si and FCC-A1 (Cu-rich)+δ-Ni2Si+ε-Ni3Si2 in the Cu-rich portion of 300-600 ℃ isothermal section phase diagram in Cu-Ni-Si alloy system. For this reason, the alloy located in the Cu-rich portion may precipitate γ-Ni5Si2, δ-Ni2Si and ε-Ni3Si2, and the proportion of each phase depends on the alloy composition and aging temperature.
2) TEM results of Cu-3.2Ni-0.75Si alloy indicate that the precipitates are mainly δ-Ni2Si phases, and only a few γ-Ni5Si2 phases, which agrees well with the thermodynamic calculation results of phase equilibria.
Acknowledgements
The authors are very grateful to Prof. C. P. Wang, Prof. X. J. Liu and Ms M. Z. Wen for assistance of calculation of phase diagram.
References
[1] PLEWES J T. High-strength Cu-Ni-Sn alloys by thermo-mechanical processing[J]. Metall Trans A, 1975, 6: 537-544.
[2] ZHAO J C, NOTIS M R. Spinodal decomposition, ordering transformation, and discontinuous precipitation in a Cu-15Ni-8Sn alloys[J]. Acta Mater, 1998, 46(12): 4203-4218.
[3] MIETTINEN J. Thermodynamic description of the Cu-Ni-Sn system at the Cu-Ni side[J]. CALPHAD, 2003, 27: 309-318.
[4] RENSEI F. Development of copper alloy for lead frame[J]. Journal of the Japan Copper and Brass Research Association, 1997, 36(1): 25-32.
[5] LOOCKYER S A, NOBLE F W. Precipitate structure in Cu-Ni-Si alloy[J]. Journal of Materials Science, 1994, 29: 218-226.
[6] FUJIWARA H. Effect of alloy composition on precipitation behavior in Cu-Ni-Si alloy[J]. Japan Inst Metals, 1998, 62(4): 301-309.
[7] LOOCKYER S A, NOBLE F W. Fatigue of precipitate strengthened Cu-Ni-Si alloy[J]. Mater Sci Technol, 1999, 15(10): 1147-1153.
[8] WANG C P, LIU X J, JIANG M, OHNUMA I, KAINUMA R, ISHIDA K. Thermodynamic database of the phase diagrams in copper base alloy systems[J]. Journal of Physics and Chemistry of Solids, 2005, 66: 256–260.
[9] SOKOLOVSKAYA E M, CHERCHERNIKOVA O I, GLADYSHEVSKIY E I. The Ni-Cu-Si system[J]. Russian Metallurgy, Translated from Izvestiya Akademii Nauk SSSR, Metally, 1973(6): 114-118.
[10] DINSDALE A T. SGTE data for pure elements[J]. CALPHAD, 1991, 15: 317-425.
Foundation item: Project(2006DFB53050) supported by the International Science and Technology Cooperation Project of the Science and Technology Ministry of China
Corresponding author: LU De-ping; Tel:+86-791-8177574; E-mail: ludeping61@163.com
(Edited by YUAN Sai-qian)