单段爆破震动的动态响应分析

凌同华^{1, 2}，李夕兵²，王桂尧¹

 (1. 长沙理工大学 桥梁与结构工程学院，湖南 长沙，410076；

2. 中南大学 资源与安全工程学院，湖南 长沙，410083)

摘  要：利用反应谱理论对单段爆破的地震效应进行研究。根据单自由度体系反应谱理论，采用计算量少、精确度高的三角插值解析公式法取代常用的分段线性插值法进行反应谱数值计算；结合工程爆破地震实测资料，对不同爆炸参量下产生的单段爆破震动信号进行反应谱分析，探讨爆炸参量对爆破震动反应谱的影响。研究结果表明，单段爆破产生的震动其频率成分相对简单；单段爆破震动的动态响应特征与爆炸参量有着密切的关系，特别是最大段药量对其影响最大。该方法可用于研究爆破地震效应特别是爆破震动危害控制和预测。

关键词：爆破地震效应；反应谱；三角插值；单自由度体系

中图分类号：TD235.1         文献标识码：A         文章编号：1672-7207(2007)03-0551-04

Dynamic response analysis of single-interval-time in

millisecond blast vibration

LING Tong-hua^{1, 2}，LI Xi-bing²，WANG Gui-yao¹

 (1. School of Bridge and Structure Engineering, Changsha University of Science and Technology, Changsha 410076, China;

2. School of Resources and Safety Engineering, Central South University, Changsha 410083, China)

Abstract: Seismic effect of single-interval-time in millisecond blast was studied by means of response spectrum. Based on response spectrum of system with one degree of freedom, response spectrum was calculated using analytical expression of trigonometric interpolation with great efficiency and high precision in calculation instead of segmented linear interpolation. According to the monitoring data from engineering blast, vibration signals of single-interval-time in millisecond blast with different explosion parameters were analyzed by response spectrum, and the influence of explosion parameters on response spectrum of single-interval-time in millisecond blast was principally explored. The results show that the frequency composition is simple relatively in blast vibration induced by single-interval-time; response characteristics of blast vibration in structure have close relation to explosion parameters, especially, the influence of maximum decking charge. It can be used to study blast seismic effect to control and forecast blast vibration damage.

Key words: blast seismic effect; response spectrum; trigonometric interpolation; system with one degree of freedom

爆破震动破坏效应的实质是一个动态破坏问题，因此，估计结构体在爆破震动作用下的反应，较为理想的方法是将实际的地面运动输入结构体并进行动力分析^[1]。事实上，从动力学方法入手分析结构体对爆破震动的动力响应过程，已成为研究震动对结构体破坏的一种主要方法^[2-6]。目前，在地震工程中应用比较成熟的反应谱理论成为分析结构体在不同动力条件下对爆破震动响应的重要手段^[7-9]。在此，本文作者结合工程爆破地震监测资料，对不同爆炸参量下产生的单段爆破震动信号进行反应谱分析，探讨爆炸参量对爆破震动反应谱的影响，了解结构体对爆破震动响应的特点。1  反应谱理论及其数值计算

1.1  反应谱理论

反应谱理论是以单自由度粘性阻尼体系在实际地震过程中的反应为基础进行结构反应分析^[1]。由反应谱曲线可以计算在一定振动载荷作用下结构体的动力反应，这就是说，任何1条反应谱曲线都是许多具有不同动力特性的单质点结构对一个地震动时程的动力最大反应按时间排列的结果^[7]。在实际应用中，常用体系的最大速度反应与体系自振周期的函数关系来表示反应谱曲线，即满足以下运动方程：

这样，当爆破地震波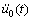作用于某一具有确定自振圆频率的振动体系时，通过求解⑴式可以得到该结构体的最大振动响应速度；同样，若改变自振圆频率ω，即ω取一系列值时(此时ω不同的取值代表具有不同圆频率的振动体系)，可以得到一系列最大速度绝对值与对应圆频率的反应谱曲线。

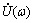在实际应用中，常用到“速度放大倍数”的概念。速度放大倍数是指体系最大反应速度与爆破地震波输入体系的最大速度的比值^{[1, 6]}，即

以β(无量纲)作纵坐标，ω (或周期T)作横坐标，所形成的曲线β(ω)或β(T)称为标准反应谱。标准反应谱反映了结构体对爆破震动的选择放大作用，体现出结构体对爆破震动响应时的动力效应。

1.2  反应谱的数值计算

反应谱的数值计算方法有许多，如褶积计算法、中点加速度法、直接积分法^[9-10]。为提高计算精度，可采用许多插值计算法，如三次样条函数求积法^[10]、抛物线内插反应谱计算方法^[11]、三角插值解析公式法^[12]以及分段线性插值法等。三角插值解析公式法直接从运动方程(1)出发，通过求得其右端扰力项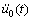，从而求得输入加速度。与其他计算法比较，该方法具有计算量少、精确度高的特点。在此，本文作者根据三角插值解析公式法用Matalab语言编制反应谱数值计算程序。

2  单段爆破震动的动态响应特征

2.1  爆破振动测试

用EXP2850爆破振动分析仪(最高采样频率为50 kHz)和CDJ-1型速度传感器(可测频率范围为2~500 Hz)对单段爆破进行爆破振动测试，从中抽取3条信号(EXP2850爆破振动分析仪自带的数据分析软件可以实现速度与加速度间的相互转换)进行反应谱分析，其爆破条件、测点位置见表1，爆破震动加速度-时程曲线见图1。

表1  测试点的爆破条件

Table 1  Condition of blast vibration measurement

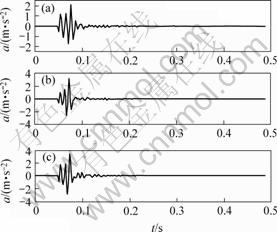
(a)—测点1；(b)—测点2； (c)—测点3

图1  单段爆破震动加速度-时程曲线

Fig.1  Acceleration-time curves of blast vibration signals

2.2  爆破振动反应谱

对于实际的构(筑)物，其阻尼比ξ一般为0.02~0.05^[13-16]，而在工程抗震计算中常取结构振动阻尼比ξ=0.05。根据运动方程⑴，采用三角插值解析公式法对图1所示信号分别进行反应谱数值计算，各信号对应的速度反应谱曲线见图2，对应的速度标准反应谱曲线见图3。

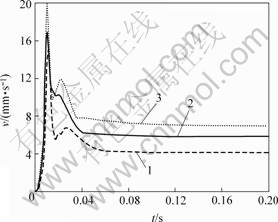
1—测点1；2—测点2；3—测点3

图2  单段爆破速度反应谱曲线

Fig.2  Velocity response spectrum curves of blast vibration signals

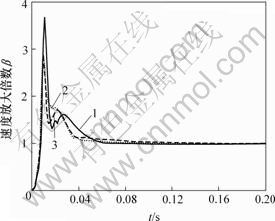
1—测点1；2—测点2；3—测点3

图3  各测点速度标准反应谱曲线

Fig.3  Standard response spectrum curves of blast vibration signals

2.3  单段爆破震动的动力响应特征分析

对图2以及图3进行分析可知，单段爆破震动的动力响应具有如下特征：

a. 单段爆破震动信号的反应谱和标准反应谱曲线的形态较简单，“突峰”数量较少，表明单段爆破产生的震动其频率成分相对简单。

b. 随着段药量的增加，速度反应谱峰值亦相应增大。表明结构体对爆破震动响应的最大值主要取决于最大段药量。

c. 随着段药量的增加，虽然速度反应谱的峰值强度增加，但其相应的标准反应谱曲线峰值没有类似特点。这表明爆破震动波在传播过程中，速度放大倍数主要取决于结构体本身，不同的结构体(具有不同的自振频率)对地震波的选择放大作用不同。

d. 随着测点到爆源距离的增加，爆破地震波的速度反应谱峰值强度降低。这表明爆破地震波在由近及远传播时，随着地震波的振动强度不断减小，反应谱峰值也相应减小；而且随着段药量增加，这种减小的趋势加强。

3  结  论

a. 单段爆破产生的震动频率成分相对简单，震动能量相对集中。

b. 爆破地震波在传播过程中，速度放大倍数主要取决于结构体本身，不同的结构体对地震波的选择放大作用不同。

c. 随着段药量的增加，速度反应谱峰值所对应的频率有降低趋势，在实施微差爆破时，必须严格控制最大段药量。

参考文献：

[1] 张雪亮，黄树棠. 爆破地震效应[M]. 北京: 地震出版社，1981.

ZHANG Xue-liang, HUANG Shu-tang. Effect of blasting ground vibration[M]. Beijing: Earthquake Press, 1981.

[2] 丁刚德，王伟策，陈小波. 微差爆破的爆破地震反应谱分析[J]. 爆破，1997，14(3): 24-29.

DING Gang-de, WANG Wei-ce, CHEN Xiao-bo. Analysis on blasting vibration response of short delay blasting[J]. Blasting, 1997, 14(3): 24-29.

[3] Kaul M K. Stochastic characterization of earthquake through their response spectrum[J]. Earthquake Engineering and Structural Dynamics, 1978, 6: 497-509.

[4] Bismarck-Nasr M N, De Oliveira M. On enhancement of accuracy in direct integration dynamic response problems[J]. Earthquake Engineering and Structural Dynamics, 1991, 20(7): 699.

[5] 李玉民，倪芝芳. 地下工程开挖爆破的地面振动特征[J]. 岩石力学与工程学报, 1997, 16(3): 274-278.

LI Yu-min, NI Zhi-fang. The characteristics on surface vibration of blasting in underground engineering[J]. Chinese Journal of Rock Mechanics and Engineering, 1997, 16(3): 274-278.

[6] 杨孟刚，胡建华，陈政清. 独塔自锚式悬索桥地震响应分析[J]. 中南大学学报: 自然科学版，2005, 36(1): 133-137.

YANG Meng-gang, HU Jian-hua, CHEN Zheng-qing. Seismic response analysis of self-anchored suspension bridge with single-towe[J]. Journal of Central South University: Science and Technology, 2005, 36(1): 133-137.

[7] 李 杰. 几类反应谱的概念差异及其意义[J]. 世界地震工程, 1993, 9(4): 9-14.

LI Jie. Several response spectrums’ conception difference and their significance[J]. World Information on Earthquake Engineering, 1993, 9(4): 9-14.

[8] 王祥厚，李明勇. 爆破地震效应强度与爆破地震荷载的探讨[J]. 贵州工业大学学报, 2000，29(2)：18-22.

WANG Xiang-hou, LI Ming-yong. Study on the strength effect and load of blasting vibration[J]. Journal of Guizhou University of Technology, 2000, 29(2): 18-22.

[9] 陈 纬. 地震加速度反应谱拟合的直接法研究[J]. 工程力学，2000, 17(1): 83-87.

CHEN Wei. Direct method of simulating response spectrum of earthquake acceleration[J]. Engineering Mechanics, 2000, 17(1): 83-87.

[10] 娄建武, 龙 源, 方 向, 等. 基于反应谱值分析的爆破震动破坏评估研究[J]. 爆炸与冲击, 2003, 23(1): 41-46.

LOU Jian-wu, LONG Yuan, FANG Xiang, et al. Study on blasting vibration damage based on response spectrum[J]. Explosion and Shock Waves, 2003, 23(1): 41-46.

[11] 蔡长青，沈建文. 抛物线内插反应谱计算方法[J]. 世界地震工程，2001，17(1): 87-92.

CAI Chang-qing, SHEN Jian-wen. Calculation of response spectrum by parabolic interpolation[J]. World Information on Earthquake Engineering, 2001, 17(1): 87-92.

[12] 朱 敏, 朱镜清. 反应谱计算的三角插值解析公式法[J]. 世界地震工程, 2001, 17(3): 62-64.

ZHU Min, ZHU Jing-qing. Calculation of response spectrum based on trigonometric interpolation[J]. World Information on Earthquake Engineering, 2001, 17(3): 62-64.

[13] 刘 华，王文辉. 大朝山单跨拱桥爆破震动速度反应谱特征[J]. 爆破, 2002, 19(4): 68-70

LIU Hua, WANG Wen-hui. Characteristics of reaction spectra of explosion vibration velocity in blasting the Dachaoshan mono-arch bridge[J]. Blasting, 2002, 19(4): 68-70

[14] 吴腾芳，王 凯，季茂荣. 反应谱分析在工程微差爆破地震监测中的应用与研究. 兵工学报，1998, 19(3): 271-274

WU Teng-fang, WANG Kai, JI Mao-rong. Vibrational response spectra in millisecond blasting[J]. ACTA Armamentarii, 1998，19(3): 271-274

[15] 何姣云, 吴新霞, 钱胜国. 大坝爆破地震的动力响应计算[J]. 爆破, 2002, 19(4): 1-3.

HE Jiao-yun, WU Xin-xia, QIAN Sheng-guo. Calculation of dynamic response of seism in dam blasting[J]. Blasting, 2002, 19(4): 1-3.

[16] 胡聿贤. 地震工程学[M]. 北京: 地震出版社, 1988.

HU Yu-xian. Earthquake engineering[M]. Beijing: Earthquake Press, 1988

收稿日期：2006-11-12

基金项目：中国博士后基金资助项目(2004036430)

作者简介：凌同华(1968-)，男，湖南双峰人，博士后，副教授，从事岩土工程及其灾害控制技术研究

通讯作者：凌同华，男，副教授；电话：0731-5040496；E-mail: lingtonghua@163.com