原子质量比对一维Fibonacci链热传导性质的影响
徐慧，崔麦玲，马松山
(中南大学 物理科学与技术学院，湖南 长沙，410083)
摘要：用传输矩阵的方法，研究一维Fibonacci链中2种不同原子的原子质量比对其热传导性能(透射系数及热导率)的影响。研究结果表明：随着原子质量比的增大，高频区域的透射系数减小，透射谱向低频方向移动；同时,原子质量比越大，同样大小的体系对应的热导率越小，当原子质量比足够大时，热导率会趋近0 W/(m?K)。在热导率与频率平方的关系曲线中，热导率随频率平方呈现台阶式缓慢上升的趋势，且在高频端趋于某一稳定值。
关键词：传输矩阵；透射系数；振动局域态；热传导
中图分类号：TB303 文献标志码：A 文章编号：1672-7207(2011)08-2351-05
Influence of ratio of atomic mass on heat conduction in one-dimensional Fibonacci chain
XU Hui, CUI Mai-ling, MA Song-shan
(School of Physical Science and Technology, Central South University, Changsha 410083, China)
Abstract: By making use of the method of transfer matrix, the behaviors of heat conduction in one-dimensional Fibonacci chain under the influence of the ratio of atomic mass (including transimission coefficient and thermal conductivity) was studied. The results show that: With the increase of the ratio of atomic mass, transmission coefficient of the high-frequency region decreases, and the transmission spectrum moves to the lower frequency region. Meanwhile, with the increase of the ratio of atomic mass, the thermal conductivity of systems decreases. When the ratio of atomic mass is large enough, the thermal conductivity of systems will tend to 0 W/(m?K). In the figure of thermal conductivity and frequency squared, the thermal conductivity shows a slowly increasing trend in the way of steps with the increase of frequency squared, and tends to be a certain value in the high-frequency region.
Key words: transfer matrix; transmission coefficient; phonon localization of vibration state; heat conductivity
早在19世纪初，人们已经认识到地球内部存在温度梯度。为了解释与之相关的一些物理现象，傅里叶于1808年提出了傅里叶热传导定律[1]。自此之后，对该定律微观机制的研究引起了人们广泛的兴趣。现在，人们可以利用分子动力学方法研究数以万计的粒子组成的体系的动力学行为，并关注一维体系热传导性质的研究。事实上，一维体系热传导的很多性质是在数值模拟中发现的。对谐振子晶格链和单原子Toda链的研究结果表明，体系中不能形成温度梯度，体系的热导率在热力学极限下趋于无穷大[2-3]。Gendenmen等[4]研究了Ding-a-Ding模型，数值证明了傅里叶热传导定律在一维体系中同样成立。后来，在对Ding-Dong模型的研究中人们也得到了相类似的结论[1]。Lepri 等[5]通过在Fermi-Pasta-Ulam (FPU)链的两端各连接上一个Noosé-Hoover热库，发现体系中形成了线性的温度分布，但体系的热导率κ与粒子数N存在幂指数关系
，且α≈0.50。此后，在对双原子Toda链[6]、琼斯流体模型[7-8]、一维槽(Channel)模型[9]、碳-纳米管等[10]的研究也发现了这种幂指数关系，现在称为反常的热传导现象。另一方面，研究表明：对于Frenkel-Kontorova模型[11]，
链[12]等具有格点势(on-site potential)的一维晶格体系热传导行为服从傅里叶热传导定律。因此，对于傅里叶热传导定律在一维体系中成立的充分和必要条件的研究引起了人们极大的兴趣。Hu等[13]通过对比研究FPU-β链和链的热传导性质，认为非可积性是体系中形成温度梯度的必要条件，但不是傅里叶热传导定律在一维体系中成立的充要条件。Narayan 等[14-15]通过运用重整化群理论分析了一维流体的输运方程，证明了一维体系中反常热传导现象存在的合理性，并且得到了α=0.33的指数值，认为该指数值对动量守恒的一维体系是普适的。然而，在对其他的一维体系模型的研究中人们还发现了一些不同的指数值[16]。直到今天，人们对一维体系中的热传导性质的认识还很不完善，还需要开展大量的理论研究和实验研究。最近，更加接近于真实体系特征的一维体系模型受到了人们的重视。Wang等[17-18]经研究发现：在同时考虑链中原子的横向运动和纵向运动后，有3种指数值，若只考虑体系粒子的纵向运动，则α=0.33；若考虑粒子的横向运动和纵向运动中等强度耦合的情况，则α=0.40。本文作者选取的研究模型为准周期模型，即一维Fibonacci链。自从Shechema等[19]在实验上发现准晶这种特殊结构的固态物质以来，人们对准晶的电学性质、热学性质、光学性质和磁学性质等进行了研究，并从理论上构造了许多准周期序列模型探讨它们的物理规律，如Fibonacci模型、广义Fibonacci模型、Penrose模型等。而Fibonacci模型作为最简单的一种准周期模型，为人们对周期性结构和随机结构的中间区域进行深入了解提供了便利。因此，研究Fibonacci模型的热传导性质对了解准周期体系的热传导性质有着重要的意义。此外，文献[20-21]从弹性波方程出发，利用传输矩阵的方法研究了n-mer体系、准周期Fibonacci链等模型的声子热传导性质，但并未考虑格点的原子质量比对其的影响。在此，本文作者在其基础上重点考虑了格点的原子质量比的作用，进一步研究一维Fibonacci链的热传导性质。
1 Fibonacci链模型和计算方法
Fibonacci链由下列递推关系生成[22]：
，其中m≥1，称为Fibonacci代。在本文中，取S0=B，S1=A。其中A和B分别代表2种不同类型的格点原子，这样构造的{Sm}序列具有如下的结构形式：
…
令Fm为第m代序列的格点原子数，习惯上被称为Fibonacci数，遵循递推关系Fm+1=Fm+Fm-1，初始条件为F0=1，F1=1。
只考虑最近邻格点之间的相互作用(紧束缚近似下)，一维Fibonacci链原子的运动方程可表示为：
(1)
其中：μi为第i个格点偏离平衡位置的位移；mi为第i个格点的质量；ω为振动频率；Ki+1,i和Ki,i-1为最近邻原子间的力作用常数；在本文中，设2种格点原子的质量分别为mA和mB，最近邻原子的力作用常数设为KAA，KAB和KBA 3种(从Fibonacci链的建构机制可以看出，链中不可能有2种B型原子处于最近邻状态)。为了简单，特设KAB=KBA，并令β=mB/mA (即原子质量比)，γ=KAA/KAB(即力作用常数比)。则式(1)可变换成下列递归形式：
(2)
其中：
，Pi是μi和μi±1之间的传输矩阵。因此，总的传输矩阵可表示为：
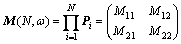(3)
式中：N为整条链中的原子数；Mi,j为总传输矩阵的矩阵元。设总传输矩阵的迹为TrM声子在允带区域中频率需满足下列条件[23]：
|TrM| ≤2 (4)
从总传输矩阵的矩阵元中，可以求出透射系数t(N，ω)的表达式如下：
(5)
其中：
，
。
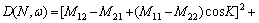
为进一步研究该体系的热传导性能，有必要计算它的热导率。本文考虑的是Rubin-Green热源[24-25]，链首尾两端的2个原子分别连着平衡温度为TL和TR的2个热库。利用Rubin-Green公式：
(6)
可以计算体系的热流密度J。其中：t(N，ω)是透射系数。由于频率大于3.5时，t(N，ω)大都已为零。为计算方便，令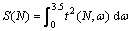
，利用矩形方法可先求出S(N)。再根据Fourier定律：
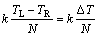，可以得到体系的热导率：
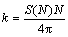(7)
2 结果和讨论
在本文中，固定N和γ，主要考虑原子质量比β的变化，计算N=610，γ=1.2，β=1.5，2.0，3.0，5.0时4种情况下格点原子质量比对一维Fibonacci链热传导性质的影响。
图1给出了不同原子质量比时透射系数与频率平方的关系。从图1(a)可看出：透射谱分布的范围很广，除了低频区有较密集的共振峰外，高频区也出现很多共振峰，且透射系数较大，在1.00~1.25和2.25~2.75处出现带隙。对比图1(a)，(b)，(c)和(d)可知，原子质量比对透射系数有很大的影响；随着原子质量比的增大，透射谱分布的范围变窄，高频区的共振峰减少，透射系数减小，而低频区透射系数仍然很大。图1(d)中高频区已不再出现共振峰。整体上，透射谱向低频方向移动。因此，可以通过调节原子质量比来实现高频区带隙宽度的调节，有效地阻隔某些频率范围内的弹性波，从而可用于制作带阻滤波器[26]。
为了进一步验证上述变化规律，进一步计算了γ=2的情况(图2)，同样可以得出相同的结论。通过多次尝试发现：当γ取不同的值时，原子质量比对透射系数的影响规律相同，都是随着原子质量比的增大，声子在高频区域的透射系数减小，透射谱向低频方向移动。
可以认为，透射系数对原子质量比的这种较强的依赖关系的原因在于：固体的热传导是晶格振动的结果。在原子链中，原子质量比增大，晶格振动的频率减小，从而高频声子的频率减小，所以，透射谱向低频区移动。而由于低频声子对晶格精细结构不敏感，故即使原子质量比很大，低频区共振峰数目仍然很多，且峰值很大。另外，声子在传输过程中受到散射，高频声子与原子碰撞过程中损失部分能量，频率降低，从而使部分高频声子转化为中频或低频声子。也就是说，当原子质量比增大时，准周期原子链的缺陷程度提高，对应的透射谱的连续性逐渐降低。故透射谱分布范围变窄，共振峰数目减少，高频区的带隙宽度增大，透射谱向低频方向移动。
图1 透射系数TE与频率平方ω2的关系
Fig.1 Relationships between frequency squared ω2 and transmission coefficient TE
图2 透射系数与频率平方的关系
Fig.2 Relationships between frequency squared and transmission coefficient
图3和图4显示不同原子质量比的热导率与系统大小和声子频率平方的关系。由图3可知：热导率随系统大小的增大而增大。同时，热导率对原子质量比同样有较强的依赖关系，原子质量比越大，同样大小的体系对应的热导率越小，即热导率对系统大小的依赖性会减弱。当原子质量比足够大时，热导率会趋近0 W?m-1?K-1。通过对图3(a), (b), (c)和(d)数据拟合，分别得出以下指数关系：
，
，
，
。可以看出：热导率κ和系统大小N同样满足关系式，并且原子质量比越大，α越小。从图4可以看出：随着声子频率的增加，热导率整体上呈现台阶式上升的趋势。与相应的透射谱对比可发现：在平台处的频率区域对应着透射谱中的禁带区域(即带隙位置)，上升处的频率对应着共振峰处的频率(即共振频率)，而在高频区，由于透射系数为零，所以，热导率在高频端趋于某一稳定值。同时，由于透射谱随着原子质量比的增大向低频方向移动，故台阶数目减少并向低频方向移动。这主要是因为：热导率源于声子的振动模，由于随着原子质量比的增大，高频区透射系数减小，允带范围变窄，故导致相同体系的热导率减小。同时，由于声子只能在允带区域内传播，在禁带区域不能传播，故在禁带区域会出现平台；而在共振频率处，体系重新为声子传播打开了通道，故热导率会急剧上升。所以，随着声子频率的增加，体系热导率呈现出台阶式上升的特性。
图3 热导率κ与系统大小N的关系
Fig.3 Relationships between system size N and thermal conductivity
图4 热导率κ与频率平方ω2的关系
Fig.4 Relationships between frequency squared and thermal conductivity
同时，对照图4(a), (b), (c)和(d)可以发现：随着原子质量比的增大，体系的热导率下降，平台数目减少，这和透射谱中的带隙数目减少相对应。原因同样在于：原子质量比增大，晶格振动的频率减小，从而声子的频率减小，导致声子向前传输更困难，从而导致透射系数和热导率的下降。
3 结论
(1) 利用传输矩阵的理论，研究原子质量比对一维Fibonacci链的透射系数的影响。结果发现：随着原子质量比的增大，高频区域的透射系数会减小，逐渐出现带隙，且带隙向低频处扩展，整个透射谱会向低频方向移动。
(2) 根据Rubin-Green公式进一步探讨了原子质量比对一维Fibonacci链的热导率的影响。发现随着原子质量比的增大，同样大小的体系对应的热导率越小，当原子质量比足够大时，热导率会趋近0 W?m-1?K-1。在κ-ω2曲线中，热导率会呈现台阶式缓慢上升的趋势，且在高频端趋于某一稳定值。
参考文献：
[1] Lepri S, Livi R, Politi A. Thermal conduction in classical low-dimensional lattices[J]. Physics Reports, 2003, 377(1): 1-80.
[2] Gillan M J, Hokkiway R W. Transport in the Frenkel-Kontorova model Ⅱ: Thermal conductivity[J]. J Phys C: Solid State Physics, 1985, 18(30): 5705-5720.
[3] Payton D N, Rich M, Visscher W M. Lattice thermal conductivity in disordered harmonic and anharmonic crystal models[J]. Physics Review, 1967, 160(3): 706-711.
[4] Gendenmen O V, Savon A V. Normal heat conductivity of the one-dimensional lattices with periodic potential of nearest-neighbor interaction[J]. Physics Review Letter, 2000, 84(11): 2381-2384.
[5] Lepri S, Livi R, Politi A. Heat conduction in chains of nonlinear oscillators[J]. Physics Review Letter, 1997, 78(10): 1896-1899.
[6] Hatano T. Heat conduction in the diatomic Toda lattice revisited[J]. Physics Review E, 1999, 59(1): R1-R4.
[7] Mareschar M, AmellaL A. Thermal conductivity in a one-dimensional Lennard-Jones chain by Molecular dynamics[J]. Physics Review A, 1988, 37(6): 2189-2196.
[8] Jachson E A, Mistrion D. Thermal conductivity of one- and two-dimensional lattices[J]. Phys: Condens Matter, 1989, 1(7): 1223-1238.
[9] Maruyama S. A molecular dynamics simulation of heat conduction in finite length SWNTs[J]. Physics B, 2002, 323: 193-195.
[10] Savin A V, Zolotaryuk A V. Heat conduction in one-dimensional systems with hard-point interparticle interactions[J]. Physics Review Letter, 2002, 88(15): 154301-4.
[11] Hu B, Li B, Zhao H. Heat conduction in one-dimensional chains[J]. Physics Review E, 1998, 57(3): 2992-2995.
[12] Aoki K, Kusnezov D. Nonequillibrium statistical mechanics of classical lattice φ4 Field theory[J]. Annals of Physics, 2002, 295(10): 50-80.
[13] Hu B, Li B, Zhao H. Heat conduction in one-dimensional nonintergrable systems[J]. Physics Review E, 2000, 61(4): 3828-3831.
[14] Narayan O, Ramawasy S. Anomalous heat conduction in one-dimensional momentum-conserving systems[J]. Physics Review Letter, 2002, 89(20): 200601-4.
[15] Prosen T, Campbll D K. Momentum conservation implies anomalous energy transport in 1D classical lattices[J]. Physics Review Letter, 2000, 84(13): 2857-2860.
[16] Maruyama S. A molecular dynamics simulation of heat conduction in a carbon nanotube[J]. Physics B, 2002, 323(4): 361-363.
[17] Wang J, Li B. Intriguing heat conduction of a chain with transverse motions[J]. Physics Review Letter, 2004, 92(7): 074302-4.
[18] Wang J, LI B. Mode-coupling theory and molecular dynamics simulation for heat conduction in a chain with transverse motions[J]. Physics Review E, 2004, 70(13): 021204-16.
[19] Shechema D, Blech I, Gratias D. 1984 Physics Review Letter, 53(20): 1951-1953.
[20] CAO Lin-san, PENG Rui-wu, ZHANG Rui-li, et al. Delocalization of phonons and quantized thermal conductance in a random n-mer system[J]. Physics Review B, 2005, 72(21): 214301-7.
[21] Enriqre M. Thermal conductivity of one-dimensional Fibonacci quasicrystals[J]. Physics Review B, 2000, 61(10): 6645-6653.
[22] HUANG Xiu-qing, GONG Chang-de. Property of Fibonacci numbers and the periodiclike perfectly transparent electronic states in Fibonacci chains[J]. Physics Review B, 1998, 58(2): 739-744.
[23] Belltsard J, Iochum B, Scoppola E, et al. Spectral properties of one dimensional quasi-crystals[J]. Maths Physics, 1989, 125(3): 527-543.
[24] Cedric B. Thermal conductivity for noisy disordered Harmonic chain[J]. J Stat Physics, 1989, 133(3): 417-433.
[25] Davies E B. A Model of Heat Conduction[J]. Journal of Statistical Physics, 1978, 18(2): 161-170.
[26] 曹永军, 杨旭. 广义Fibonacci准周期结构声子晶体透射性质的研究[J]. 物理学报, 2008, 57(6): 3620-3624.
CAO Yong-jun, YANG Xu. Transmission properties of the generalized Fibonacci quasi-periodical phononic crystal[J]. Acta Phys Sin, 2008, 57(6): 3620-3624.
(编辑 陈爱华)
收稿日期：2010-08-22；修回日期：2010-11-19
基金项目：中国高等学校博士点专项科研基金资助项目(20070533075)；湖南省科技计划项目(2009FJ3004)
通信作者：徐慧(1958-)，男，湖南常德人，博士，教授，从事无序材料电子结构和热学性质研究；电话：0731-88836762；E-mail：cmpxhg@mail.csu.edu.cn
