DOI: 10.11817/j.issn.1672-7207.2015.02.036
折线型滑面边坡强度参数反演的极限分析上限法
陈静瑜1, 2,赵炼恒1,李亮1,谭捍华3
(1. 中南大学 土木工程学院,湖南 长沙,410075;
2. 华东交通大学 轨道交通学院,江西 南昌,330000;
3. 贵州省交通规划勘察设计研究院股份有限公司,贵州 贵阳,550001)
摘要:基于极限分析上限定理,考虑孔隙水压力的影响,提出折线型滑面边坡稳定分析计算模型。根据相关联流动法则和内外能耗守恒原理,结合强度折减技术,对折线型滑面边坡稳定性进行分析,得出折线型滑面边坡稳定性极限分析上限解。假定滑坡处于极限平衡状态,即安全系数Fs=1.0,求解不同断面一系列的c和φ组合,然后用图解法确定边坡滑面的抗剪强度参数,不同断面的c-φ曲线的交点即为抗剪强度参数的反演值。以湘西朱雀洞特大滑坡为工程实例进行抗剪强度参数反演分析,并与现场勘测的强度参数进行比较分析。研究结果表明:本文方法有效,反演结果可为相似工程的强度参数确定提供有益参考。
关键词:参数反演;极限分析上限法;垂直分条;破坏机构;安全系数
中图分类号:TU437 文献标志码:A 文章编号:1672-7207(2015)02-0638-07
Back-analysis of shear strength parameters for slope with broken line sliding surface based on upper bound approach
CHEN Jingyu1, 2, ZHAO Lianheng1, LI Liang1, TAN Hanhua3
(1. School of Civil Engineering, Central South University, Changsha 410075, China;
2. School of Railway Tracks and Transportation, East China Jiaotong University, Nanchang 330000, China;
3. Guizhou Communication Planning and Prospecting Design Academy, Guiyang 550001, China)
Abstract: A new computational model for stability analysis of slope with the broken line sliding surface was presented based on the upper bound theorem with the influence of pore water pressure taken into consideration. In combination with the strength reduction technique, the stability of slope with broken line sliding surface was studied, and the upper bound solutions of safety factor for slope with the broken line sliding surface was obtained according to the associated flow rule and the internal and external energy conservation principle. Assuming that the landslide is in limit equilibrium state, namely the safety factor Fs=1.0, a series of c and φ combinations of different sections can be back calculated. And then the graphical method was used to determine the shear strength parameters, i.e. the intersection point of c-φ curves for different sections. In order to evaluate the validity of the proposed method, the Zhuquedong landslide as an engineering project was calculated, and then compared with the field survey values. The results show that the inversion parameters of both methods are in good conformity. The back-analysis results can give useful reference for the similar engineering.
Key words: back analysis; upper bound approach; vertical slices; failure mechanism; safety factor
准确分析评价滑坡稳定性以及进行滑坡治理工程设计的关键是计算参数的选取,尤其是滑带土抗剪强度参数的选取。强度参数选取合理性与边坡工程的安全性和经济性直接相关。土工试验是获取强度参数的基本且有效的方法,对于材料的空间变异性不强的岩土体,采用试验方法技术成熟,结果可靠,被广泛地应用于工程实践中[1]。对于内部强度参数分布不均的岩土体,试样的原状性、代表性、试验方法的合理性将对试验结果造成较大影响。徐建平等[2-3]指出滑带土剪切试验受试样和试验条件的限制,滑带土试验数据通常很离散,需进行分析计算来确定。张金华[4]指出由室内试验或现场试验得到的土体强度试验数据分析确定的岩土体抗剪强度参数中的内聚力往往偏小。反演分析是抗剪强度参数估算的常用方法,它是通过已知稳定系数及滑面等条件,对边坡进行一定假设,反算滑面的综合抗剪强度参数[5-9]。反演分析综合性好,能将考虑欠缺的外部作用因素融入反演的抗剪强度参数中,使滑坡稳定性分析更切合实际,对于具有明显滑坡特征的边坡滑面参数的选取具有重要的借鉴意 义[10-12]。在目前的多数研究中,滑坡整体失稳时滑带土抗剪强度参数的反演分析都是通过极限平衡法进行计算的。易朋莹等[13]运用极限平衡原理对滑坡抗剪强度参数进行敏感性分析,得出边坡潜在滑动面c和φ关系曲线,结合试验值综合确定出边坡潜在滑动面抗剪强度参数c和φ。Fang等[14]运用不平衡推力法对武广(武汉 —广州)客运线郴州段的红黏土滑坡进行抗剪强度参数反演分析,指出对于复合边坡需进行整体和局部抗剪强度参数反演。赵淑云等[15]针对特定情况,采用极限平衡理论推导得到了关于求解强度参数c和φ的解析表达式,从而只要确定二者中的一个,另一个就容易求得。石纲等[16]采用假定c计算φ的方法反算滑面的岩土抗剪强度参数,结合滑带土室内试验和现场大剪试验,综合分析对比所得参数值,从而合理确定建议值。但是,传统的极限平衡法并没有考虑力矩平衡条件, 理论上不够严谨。基于极限分析上限定理反演滑带土抗剪强度参数,绕开了岩土材料复杂的本构关系,与极限平衡方法相比具有严格的理论基础。Chen[17]全面阐述了极限分析上限法在边坡稳定性评价中的应用。陈祖煜等[18-21]从极限分析理论出发,提出了土质边坡条分法。Michalowski等[22-26]也对多条分边坡稳定性的能量分析方法进行了研究。总之,采用极限分析方法进行滑带土抗剪强度参数的研究已成为热点,但目前采用该法进行折线型滑面边坡的抗剪强度参数反演分析的研究较少。因此,本文作者根据极限分析上限定理,考虑孔隙水压力的影响,以垂直分条折线型滑面边坡为计算模型,在参考现场勘测试验值的基础上,进行边坡滑面抗剪强度参数的反演分析,这对边坡滑面抗剪强度参数的选取具有重要的借鉴意义。
1 抗剪强度参数反演分析方法
滑动面抗剪强度参数选择的正确性直接影响滑坡稳定性验算及滑坡推力的数值。反演分析的基本前提是[9]:1) 必须知道当时坡体的安全系数;2) 滑面的确切位置已知,包括后缘拉裂缝及前缘剪出口等; 3) 查清造成坡体变形的各种外力因素。
对于一定的滑坡断面,利用极限分析上限定理,根据已知的边坡安全系数Fs,可以求得其c和φ的关系[1]。但c和φ是2个未知数,因而必须先假定一个未知数,再求另一个未知数。在实际的反演分析中,可以计算c和φ对安全系数的敏感度,对于敏感度较低的参数,可以通过试验来确定其数值,对于敏感度较高的参数,则通过参数反演获得其准确值[1]。
表1 滑坡不同发育阶段的安全系数
Table 1 Safety factor for different development stages of landslide

2个或多个滑坡断面联立反演时,会出现2条或多条平行的直线,以致无法求解的情况。因此,多断面反演分析的基本条件是所选取的多个断面必须相似,包括:1) 地质条件类似,滑坡的类型、滑带土的组成以及含水状态要相似;2) 滑坡的运动状态和过程相似,即发育阶段类似[9]。假定滑坡处于极限平衡状态,其安全系数Fs=1.0,结合边坡滑面抗剪强度参数试验值进行反演分析,求解出不同断面的一系列c和φ的组合。采用图解法,绘制不同断面的c-φ曲线,其交点即为反演所得的强度参数值,如图1所示。
2个反算断面确定的强度参数是唯一的,当反演分析的断面多于2个,且得出的强度参数差异较小时,反演分析的结果较为可靠。当其差异较大时,应校核滑坡的分析状态条件等因素,重新进行分析,直至得到理想的结果[13]。

图1 c和φ的图解示意图
Fig. 1 Sketch diagram of c and φ
2 边坡稳定性极限分析上限解
2.1 机动许可速度场
极限分析上限法也称能量法,将土体本构关系简化为理想刚塑性应力-应变关系,根据破坏机构建立虚功率方程,从而推导出滑体的稳定安全系数计算公式[17, 25, 27]。本文采用垂直分条折线型滑面边坡破坏机构(如图2所示),边坡按照折线滑面的转折点垂直离散为一系列的条块,视每一条块为刚体,滑面和条间错动的部位被视为塑性体[22]。

图2 垂直分条折线型滑面边坡破坏机构
Fig. 2 Failure mechanism of slope with broken line sliding surface divided into vertical slices
土坡处于极限破坏状态,合理的运动方向是岩滑面向下,相关联流动法则(associative flow rule)要求各土条滑面上的速度与滑面成角φ[24]。相邻土条滑面上的速度矢量vi和vi-1的矢差引起第i与第i-1相邻土条的相对速度[v]i-1, i,且vi,vi-1和[v]i-1, i组成的速度矢量要闭合,如图3所示。
根据速度矢量闭合几何关系,可以推导出相邻垂直条块的速度递推公式为:
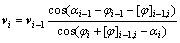 (1)
(1)
 (2)
(2)
式中:vi和vi-1为土条滑面的速度;αi和αi-1为土条滑面的倾角;φi和φi-1为土条滑面的内摩擦角; [φ]i-1,i和[v]i-1,i分别为条间竖向速度间断面的内摩擦角及相对速度。

图3 速度矢径及速度矢量图
Fig. 3 Velocity vectors and hodograph
2.2 虚功率原理
极限分析法中虚功率原理的表述是:岩土体自重和孔隙水压力所做的外功率(不考虑外荷载作用的情况)与塑性变形区的内部能量耗损率相等。
根据土塑性力学可知,土坡的滑移面是速度间断面,相邻土条的速度差使条间产生竖向速度间断面,沿速度间断面将有内能的耗散,但在条块内的内能耗散为0[24]。速度间断面单位面积内能耗散公式如下:
 (3)
(3)
式中:c和φ为沿速度间断面土的抗剪强度参数;v为速度间断面上的速度。
内部能量耗损率为
 (4)
(4)
式中:li和hi分别为第i个土条滑面长度和土条竖向间断面高度;n为土条的数量。
孔隙水压力是边坡稳定性分析中必须考虑的1个重要因素。这里采用与Michalowski[22]类似的处理方法,将孔隙水压力当作外力做功出现在虚功率平衡方程中,用来求解边坡稳定的上限解。滑体单元孔隙水压力为
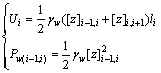 (5)
(5)
式中:Ui为作用在第i个滑体单元底滑裂面上的水压力;Pw(i-1,i)为作用在第i-1和第i个滑体单元条间竖向速度间断面上的水压力;[z]i-1,i为第i-1和第i个滑体单元条间竖向速度间断面上孔隙水深。
作用在边坡计算模型的外力包括自重和孔隙水压力,外力功率W外为:
 (6)
(6)
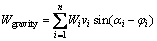 (7)
(7)
 (8)
(8)
式中:Wi为第i个土条的土体自重。
当土坡处于极限状态,根据内外功率相等的条件(D内=W外),即可建立虚功率方程[24]。
2.3 安全系数求解
极限平衡状态时,土的换算力学指标cf和φf为
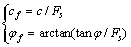 (9)
(9)
此时,式(4)中的c和φ应取极限状态时的cf和φf。将式(9)代入虚功率方程中整理后可得
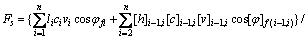
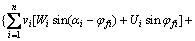
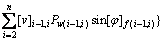 (10)
(10)
式中: ;
;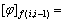
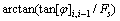 。
。
式(10)中安全系数以隐式出现,在计算时需要迭代。式中vi和[v]i-1,i可以根据式(1)和(2)进行消除。当仅考虑均质土坡时,式(10)可以简化为

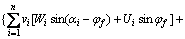
 (11)
(11)
此时,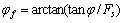 。
。
3 工程算例
湘西朱雀洞特大滑坡位于常吉(常德—吉首)高速公路第28合同段,该滑坡前缘为丹青河,滑坡周界在平面上呈圈椅状,滑坡长度448 m(垂直于常吉路方向),平均宽度约450 m,滑体平均厚度15 m,滑体体积约260万m3(图4和图5)。滑带土主要为粉砂质泥岩中软弱夹层或泥化夹层及层间错动,呈软塑土状。滑动面的下部滑床岩性主要为较为完整的弱、微风化岩。滑坡区汇水面积大,达25万多m2,地下水位受大气降水影响较大,降雨过后坡体的地下水水位迅速升高。
该滑坡周界主要受2条断层F1和F2控制,根据地貌特征、滑体物质及结构特征,在平面上分为Ⅰ,Ⅱ,Ⅲ共 3个分区(图6)。

图4 朱雀洞滑坡正面全貌
Fig. 4 Front panorama of Zhuquedong landslide

图5 朱雀洞滑坡侧貌
Fig. 5 Landslide profile of Zhuquedong

图6 滑坡断面分区平面图
Fig. 6 Planar graph of landslide section
根据现场滑坡的形态特征、勘探的地质资料及目前滑坡的稳定情况,选取Ⅱ区滑体1-1'和2-2'共2个典型断面计算滑动面的抗剪强度参数。
考虑到降雨工况是此处滑坡的最危险工况,故选用目前坡面在洪水位的工况,采用极限分析上限法,构建折线型滑面计算模型,如图7和图8所示。
计算时,把断面1-1'上的滑体划分为16个条块,把断面2-2'上的滑体划分为9个条块,主要依据钻探确定的滑面位置划分条块。滑体天然容重为18.2 kN/m3,饱和容重为21.6 kN/m3,分条数据和物理力学指标见表2和表3。
根据土坡稳定性极限分析条分法安全系数计算公式,采用Matlab编写电算程序,考虑“自重+水”的工况,进行抗剪强度参数反演计算。通过敏感性分析,发现参数c的敏感度较低,因此,根据朱雀洞特大滑坡滑面抗剪强度参数的试验值先假定参数c,然后反演φ。
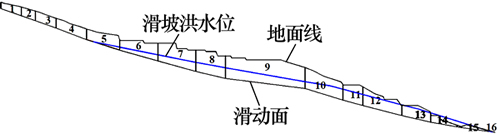
图7 朱雀洞滑坡1-1'断面计算模型
Fig. 7 Computation model of Zhuquedong landslide section 1-1'

图8 朱雀洞滑坡2-2'断面计算模型
Fig. 8 Computation model of Zhuquedong landslide section 2-2'
表2 1-1' 断面极限分析上限法反演参数
Table 2 Back-analysis parameters of section 1-1’ used by upper bound limit analysis

表3 2-2' 断面极限分析上限法反演参数
Table 3 Back-analysis parameters of section 2-2' used by upper bound limit analysis

滑坡断面1-1和2-2'的抗剪强度参数c和φ的关系曲线如图9所示。

图9 c-φ曲线反演分析
Fig. 9 Back analysis of c-φ curve
当1-1'断面的安全系数Fs=1.0时,c和φ满足
φ=-0.378 5c+17.041 (12)
当2-2'断面的安全系数Fs=1.0时,c和φ满足
φ=-0.351 0c+16.708 (13)
联立式(12)和式(13)可得同时满足要求的滑动面抗剪强度参数为c=12.11 kPa,φ=12.46°,该反演参数综合考虑了滑面的起伏及参数的不均,可以很好地反映滑坡1-1'和2-2'断面同时处于临界状态的特点。
现场勘测试验的强度参数为c=5~9 kPa,φ=10°~16°,本文极限分析上限法反演的强度参数与现场勘测试验值吻合良好,验证了本文方法在解决复杂平面边坡滑动问题的有效性和参考意义。
4 结论
1) 本文采用极限分析上限法反演得到的抗剪强度参数与现场勘测试验的结果吻合良好,证明了本文方法的有效性。
2) 反演分析受空间差异性的影响,反分析的结果难免存在误差,且参数c和φ不具有唯一性,因此,强度参数的反演分析还应参考试验值或类比值综合 确定。
3) 反演分析的断面应不少于2个,反演分析的断面越多,反演分析结果的精确度越高。
4) 地下水位对参数c和φ反演结果影响显著,考虑计算工况对计算结果的影响有待进一步讨论。基于极限分析上限法反演边坡抗剪强度参数作为一种抗剪强度参数估算的新方法,其适用性和有效性尚需要今后在更多的实际应用中验证和完善。
参考文献:
[1] 石耀华. 利用能量法的边坡强度参数反演研究[J]. 公路工程, 2012, 3(1): 203-205.
SHI Yaohua. Soil slope strength parameter back analysis on energy method[J]. Highway Engineering, 2012, 3(1): 203-205.
[2] 徐建平, 胡厚田, 张安松, 等. 边坡岩体物理力学参数的统计特征研究[J]. 岩石力学与工程学报, 1999, 18(4): 382-386.
XU Jianping, HU Houtian, ZHANG Ansong, et al. On statistical characteristics of physical and mechanical parameters in slope rockmass[J]. Chinese Journal of Rock Mechanics and Engineering, 1999, 18(4): 382-386.
[3] 林鲁生, 蒋刚, 白世伟, 等. 土体抗剪强度参数取值的统计分析方法[J]. 岩土力学, 2002, 23(5): 570-574.
LIN Lusheng, JIANG Gang, BAI Shiwei, et al. Statistica anaslysis method of taking value for shear strength parameters of soil mass[J]. Rock and Soil Mechanics, 2002, 23(5): 570-574.
[4] 张金华. 岩土体抗剪强度参数反演及滑坡灾害预测研究[D]. 重庆: 重庆交通大学河海学院, 2010: 2-4.
ZHANG Jinhua. Research on the shear strength parameters inversion of rock-soils and the prediction of landslide disaster[D]. Chongqing: Chongqing Jiaotong University. College of River and Ocean Engineering, 2010: 2-4
[5] Rozos D, Apostolides E, Christaras B. Slope stability problems in the area between St.George and St.Herene villages and their significance for the main road Argostoli-Poros on Kefallonia Island,Greece[J]. Bulletin of Engineering Geology and the Environment, 2002, 61(4): 303-309.
[6] 廖秋林, 杨志法, 尚彦军, 等. 川藏公路102滑坡滑动带力学参数的反分析[J]. 岩石力学与工程学报, 2004, 23(24): 4119-4123.
LIAO Jiulin, YANG Zhifa, SHANG Yanjun, et al. Back analysis of slip surface of the 102 landslide on Sichuan—Tibet highway[J]. Chinese Journal of Rock Mechanics and Engineering, 2004, 23(24): 4119-4123.
[7] 刘小丽, 邓建辉, 李广涛. 滑带土强度特性研究现状[J]. 岩土力学, 2004, 25(11): 1849-1853.
LIU Xiaoli, DENG Jianhui, LI Guangtao. Shear strength properties of slip soils of landslides: an overview[J]. Rock and Soil Mechanics, 2004, 25(11): 1849-1853.
[8] 陈骏峰. 降雨型堆积层滑坡抗剪强度参数反演分析[J]. 华中科技大学学报(城市科学版), 2008, 25(4): 249-253.
CHEN Junfeng. Back analysis of the shear strength parameters of rainfall-induced colluvial landslides[J]. Journal of Huazhong University of Science and Technology (Urban Science Edition), 2008, 25(4): 249-253.
[9] 郑颖人, 陈祖煜, 王恭先, 等. 边坡与滑坡工程治理[M]. 2版.北京: 人民交通出版社, 2010: 252-256.
ZHENG Yinren, CHEN Zuyu, WANG Gongxian, et al. Engineering treatment of slope and landslide[M]. 2nd ed. Beijing: China Communications Press, 2010: 252-256.
[10] Sakurai S. Field measurement and back analysis[C]//Computer Method and Advances in Geomechanics. Rotterdam: Balkema, 1992: 1693-1701.
[11] 刘迎曦, 吴立军, 韩国城. 边坡地层参数的优化反演[J]. 岩土工程学报, 2001, 23(3): 315-318.
LIU Yingxi, WU lijun, HAN Guocheng. Optimization inversion for identifying ground parameters of slope[J]. Chinese Journal of Geotechnical Engineering, 2001, 23(3): 315-318.
[12] 郑明新. 论滑带土强度特征及强度参数的反算法[J]. 岩土力学, 2003, 24(4): 528-532.
ZHENG Mingxin. Research of strength characteristic of landslide slip and revised counter calculation method[J]. Rock and Soil Mechanics, 2003, 24(4): 528-532.
[13] 易朋莹, 王凯, 任佳, 等. 基于传递系数法的滑坡滑带土强度参数反分析研究[J]. 中国地质灾害与防治学报, 2008, 19(4): 23-26.
YI Pengying, WANG Kai, REN Jia, et al. Research on anti-analysis of the landslide’s strengh parameter through transferring coefficient method[J]. The Chinese Journal of Geological Hazard and Control, 2008, 19(4): 23-26.
[14] FANG Wei, YANG Guolin, LIU Xiaohong, et al. Study on shear strength parameter back-calculation of red clay slope[J]. Geotechnical Special Publication, 2011, 216: 97-102.
[15] 赵淑云, 于清扬, 詹军, 等. 抗剪强度参数反分析取值研究[J]. 成都理工学院学报, 2001, 28(Z): 418-420.
ZHAO Shuyun, YU Qingyang, ZHAN Jun, et al. A study of the anti-analysis on determining the values of strength parameters[J]. Journal of Chengdu University of Technology, 2001, 28(Z): 418-420.
[16] 石纲, 包雄斌, 练操, 等. 重庆羊角滑坡群滑带土抗剪强度研究[J]. 人民长江, 2011, 42(22): 54-56.
SHI Gang, BAO Xiongbin, LIAN Cao, et al. Study on shear strength of slip soil of Yangjiao landslides group[J]. Yangtze River, 2011, 42(22): 54-56.
[17] Chen W F. Limit analysis and soil plasticity[M]. New York: Elsevier Scientific Publishing Cooperation, 1975: 244-274.
[18] 陈祖煜. 土质边坡稳定分析—原理·方法·程序[M]. 北京: 中国水利水电出版社, 2003: 23-63.
CHEN Zuyu. Soil slope stability analysis-theory methods and programs[M].Beijing: China Water Power Press, 2003:23-63.
[19] Donald I B, Chen Z Y. Slope stability analysis by the upper bound approach: Fundamentals and methods[J]. Canadian Geotechnical Journal, 1997, 34(6): 85--862.
[20] Chen Z Y, Donald I. Comparison between the limit equilibrium and limit analysis method[C]//Proceedings of the 10th Asian Regional Conference on Soil Mechanics and Foundation Engineer. 1995: 267-270.
[21] Chen Z Y. Morgenstern N R. Extensions to the generalized method of slices for stability analysis[J]. Canadian Geotechnical Journal, 1983, 20(1): 104-109.
[22] Michalowski R L. Slope stability analysis: a kinematical approach[J]. Geotechnique, 1995, 45(2): 283-293.
[23] 邹广电, 蒋婉莹. 边坡稳定性分析的一个改建条分法[J]. 岩石力学与工程学报, 2003, 22(12): 3368-3372.
ZOU Guangdian, JIANG Wanying. Rebuilt slice method for slope stability analysis[J]. Chinese Journal of Rock Mechanism and Engineering, 2003, 22(12): 3368-3372.
[24] 王根龙, 门玉明, 陈志新, 等. 土坡稳定性塑性极限分析条分法[J]. 长安大学学报(自然科学版), 2002, 22(4): 28-30.
WANG Genlong, MEN Yuming, CHEN Zhixin, et al. Plasticity limit analysis on soil slope stability by slice techniques[J]. Journal of Chang’an University (Natural Science Edition), 2002, 22(4): 28-30.
[25] 王根龙, 伍法权, 李巨文. 折线型滑面边坡稳定系数计算的极限分析上限解[J]. 水文地质工程地质, 2007, 34(1): 62-65.
WANG Genlong, WU Faquan, LI Juwen. Upper-bound solution of safety factor for slope with broken-line slip surface based on plasticity limit analysis[J]. Hydrogeology and Engineering Geology, 2007, 34(1): 62-65.
[26] 王根龙, 伍法权, 祁生文, 等. 加锚岩质边坡稳定性评价的极限分析上限解[J]. 岩石力学与工程学报, 2007, 26(12): 2556-2563.
WANG Genlong, WU Faquan, QI Shengwen, et al. Research on limit analysis upper bound method for stability evaluation of anchored rock slope[J]. Chinese Journal of Rock Mechanism and Engineering, 2007, 26(12): 2556-2563.
[27] 赵炼恒. 边坡稳定性与加固设计的能量分析方法[D]. 长沙: 中南大学土木建筑学院, 2009: 19-23.
ZHAO Lianheng. Energy analysis study on slope stability and reinforcing design[D]. Changsha: Central South University. College of Civil and Architectural Engineering, 2009: 19-23.
(编辑 赵俊)
收稿日期:2014-03-02;修回日期:2014-06-26
基金项目(Foundation item):国家自然科学基金资助项目(51078359,51208522);中国博士后科学基金资助项目(20110491269,2012T50708);贵州省交通运输厅科技项目(2012122033);湖南省科学技术厅科技计划项目(2012SK3231)(Projects (51078359, 51208522) supported by the National Natural Science Foundation of China; Projects (20110491269, 2012T50708) supported by the Postdoctoral Science Foundation of China; Project (2012122033) supported by the Foundation of Guizhou Provincial Transportation Department, China; Project (2012SK3231) supported by the Foundation of Science and Technology Department of Hunan Province, China)
通信作者:赵炼恒,博士后,副教授,博士生导师,从事道路与铁道工程、岩土极限分析理论等方面的工作;E-mail:zlh8076@163.com