文章编号:1004-0609(2012)02-0520-06
一种改进的纳米压入测试方法
宋仲康,马德军,郭俊宏,陈 伟
(装甲兵工程学院 机械工程系,北京 100072)
摘 要:利用过量纲理论和有限元模拟分析了Oliver-Pharr方法识别材料折合弹性模量的精度。结果表明:理论测试误差明显依赖于卸载后的残余深度与最大压入深度的比值(hf/hm)和材料的应变硬化指数n。当hf/hm>0.7、n=0时,Oliver-Pharr方法计算的折合弹性模量最大测试误差将近32%,其原因是由于估算得到的接触深度明显低于真实的接触深度。在此基础上,提出一种改进的计算方法,对接触深度的估算进行修正,应用改进方法确定材料折合弹性模量时,最大误差可控制在±15%以内。两种铝合金材料的压入试验也证明了此结论。
关键词:纳米压入;弹性模量;量纲分析;有限元方法;硬化指数
中图分类号:TH140 文献标志码:A
A modified method of nanoindentation testing method
SONG Zhong-kang, MA De-jun, GUO Jun-hong, CHEN Wei
(Department of Mechanical Engineering, Academy of Armored Force Engineering, Beijing 100072, China)
Abstract: The accuracy of reduced elastic modulus obtained by Oliver-Pharr method from nanoindentation data was analyzed by dimensional theorem and finite element simulation. The results show that the error depends on the final depth at the maximum depth ratio (hf/hm) and hardening coefficient (n) obviously. The maximum error is near upon 32% at hf/hm>0.7 and n=0 because the predicted contact depth is lower than the true contact depth. Thereby, a modified method is brought forward to amend the predicted contact depth. The maximum error of reduced elastic modulus obtained by the modified method can be controlled within ±15%. The results of two indentation tests of aluminum materials agree well with the conclusion.
Key words: nanoindentation; elastic modulus; dimensional theorem; finite element method; hardening coefficient
随着表面材料科学研究的不断深入以及以MEMS为代表的小尺度材料研究的兴起,相应材料的力学性能测试因传统方法不再适用而变得困难起来。在这种背景下,人们研制了专用于表层力学性能研究的纳米压入技术。与传统硬度试验不同,该技术通过连续高精度测量和记录样品上压头加载和卸载时的载荷和位移数据,提供比传统硬度试验更为丰富的有用信息。并以此为基础,通过构建精细的力学模型,材料的诸多力学性能参数可以被识别,如表面或界面硬度、弹性模量、屈服强度、断裂韧性、蠕变系数以及疲劳强度等[1-3]。纳米压入测试方法因其试样尺度 小、试验接近无损、测试方便等特点,受到人们广泛关注。
研究者提出了不少纳米压入测试方法[4-9],目前应用最普遍的方法是Oliver-Pharr方法[8-9],该方法通过以下关系来确定材料的折合弹性模量(Er):
 (1)
(1)
 (2)式(1)和(2)中:S为卸载曲线初始斜率(见图1);β为常数,对于Berkovich压头,β=1.034;A为投影接触面积;E、Ei和υ、υi分别为被测材料和压头的弹性模量和泊松比。图1中pm为最大压入载荷;hm为最大压入深度; hf为卸载后的残余深度。
(2)式(1)和(2)中:S为卸载曲线初始斜率(见图1);β为常数,对于Berkovich压头,β=1.034;A为投影接触面积;E、Ei和υ、υi分别为被测材料和压头的弹性模量和泊松比。图1中pm为最大压入载荷;hm为最大压入深度; hf为卸载后的残余深度。

图1 压入试验的载荷—深度曲线
Fig. 1 Load—depth curves of nanoindentation test
Oliver-Pharr方法作为经典的纳米压入测试方法,在测试压入周围凹陷变形的材料(如大多数陶瓷、硬金属和加工硬化的软金属)时,测试结果吻合得很好[10]。但由于接触深度的确定是基于线弹性小变形假设,而压入过程不可避免地要使材料进入塑性,因此,基于接触深度确定的接触面积只能是近似的。当Oliver-Pharr方法应用于低硬化水平的被测材料时,由于估算得到的接触面积明显小于真实接触面积,导致测得的硬度和弹性模量严重偏离真值。事实上,该问题在Oliver- Pharr方法提出不久就已被人们认识,BOLSHAKOV等[11]指出,在具有鼓凸(pile-up)现象发生的仪器化压入试验中,应用Oliver-Pharr方法测得的压入硬度和弹性模量可能被高估50%。OLIVER和PHARR[9]也明确指出,当压入周围出现鼓凸现象时,Oliver-Pharr方法并不适用,应采用图像法来确定接触面积,然而,采用该方法将大大降低仪器化压入测试的效率。本文作者通过量纲分析和有限元模拟分析Oliver-Pharr方法识别材料折合弹性模量的精度及影响因素,并在此基础上,提出一种改进的纳米压入测试方法,应用本方法确定材料折合弹性模量时最大理论测试误差可控制在±15%以内,远小于Oliver-Pharr方法的最大理论测试误差。
1 纳米压入问题的量纲分析和有限元模拟
由于纳米压入问题涉及复杂的材料、几何和接触边界条件非线性,因此,人们至今无法获得准确的解析解[7]。为全面分析各种材料的纳米压入响应与折合弹性模量的关系,可采用有限元方法。目前,在纳米压入测试中广泛应用的压头为Berkovich压头。研究表明,就纳米压入加、卸载曲线而言,Berkovich压头可以用圆锥压头来近似[12]。为确保圆锥压头与Berkovich压头具有相同的面积—深度关系,圆锥压头的锥半角θ取值为70.3°。建立有限元模型时,假设被压材料为均匀、各向同性、率无关固体,且遵循Von Mises屈服准则及纯各向同性强化准则,同时假设被压材料的单轴应力—应变关系由线弹性与Hollomon幂硬化函数组成[12-14],即
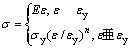 (3)
(3)
式中:σ为被压材料的真实应力;ε为被压材料的真实应变;σy为被压材料的屈服应力;εy为被压材料的屈服应变,且εy=σy/E;n为应变硬化指数。
显然,当压头为弹性体、压头与被压材料间无摩擦时,任何压入响应均可表示为被压材料的弹、塑性特性(E, ν, σy, n)、压头材料的弹性特性(Ei, νi)以及最大压入深度(hm)的函数。MA等[15]根据量纲分析,揭示压入测试时折合弹性模量的理论测试误差可表示为σy/Er和n的函数
 (4)
(4)
式中:QEr为无量纲数,代表理论测试误差;ErO-P为应用Oliver-Pharr方法测得的折合弹性模量; 为压头和被压材料的真实折合弹性模量。
为压头和被压材料的真实折合弹性模量。
下面分析卸载后的残余深度hf,它可表示为压入测试时对其产生影响的各个参数的函数
 (5)
(5)
式中:压头及被压材料弹性有关的变量可简化为一个变量[16],即折合弹性模量Er,则
 (6)
(6)
应用量纲Π定理,式(6)可简化为
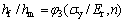 (7)
(7)
那么,σ y/Er也可表示为hf/hm的函数
 (8)
(8)
将式(8)代入式(4),则
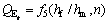 (9)
(9)
即所测折合弹性模量的理论测试误差可表示为hf/hm和n的函数。将式(1)代入式(9),可得
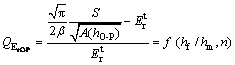 (10)
(10)
通过有限元模拟可获得式(10)的显式解。应用商用有限元软件ABAQUS对圆锥压头压入弹塑性材料的载荷—深度响应进行数值模拟。图2所示为有限元划分的压头与被压材料总体网格和靠近尖端的局部网格。其中,对压头和被压材料分别划分了3 600个和10 000个轴对称四边形单元,通过收敛性分析,表明上述网格单元可以满足0.5%的精度要求。

图2 压头与被压材料有限元网格
Fig. 2 FEM mesh of indenter and indented material: (a) Overall mesh; (b) Mesh near contact region
数值模拟时设定金刚石压头弹性模量E=1 141 GPa,泊松比υ为0.07;被测材料弹性模量E=70 GPa,泊松比υ为0.3,则由式(2)可得到真实折合弹性模量Ert=72.087 GPa。为考察不同塑性行为和加工硬化的影响,设定被测材料的屈服应力σy分别为0.002、0.004、0.008、0.016、0.035、0.07、0.14、0.28、0.56、1.12、2.24、4.48、6.65、8.75、10.5、11.9和25.2 GPa;应变硬化指数n分别取0、0.15、0.3和0.45;最大压入深度为3 μm。
利用数值模拟得到材料压入测试的载荷—深度关系曲线,应用相关方法确定材料弹性模量,并和原始值进行比较,即可得到该方法的理论测试误差。
2 Oliver-Pharr方法及其测试精度分析
2.1 Oliver-Pharr方法估算的接触深度
Oliver和Pharr基于小变形纯弹性假设,建立相关力学模型,通过下式估算接触深度
 (11)
(11)
hO-P如图3所示。则对于锥半角θ为70.3°的理想锥形压头(无尖端钝化),由几何关系可得投影接触面积
 (12)
(12)

图3 压入测试中的接触深度
Fig. 3 Contact depth in nanoindentation test
将式(12)代入式(1),即可计算折合弹性模量。
2.2 Oliver-Pharr方法测试精度分析
利用第1节有限元模拟得到的压入载荷—深度曲线,应用Oliver-Pharr方法计算折合弹性模量ErO-P,并和真实折合弹性模量Ert进行比较,令
 (13)
(13)
式中:δrO-P为Oliver-Pharr方法的识别误差,其随hf/hm和n的变化情况如图4所示。

图4 误差δrO-P随hf/hm和n的变化
Fig. 4 Plots of δrO-P changing with hf/hm and n
由图4可看出,测试误差与hf/hm值和材料的应变硬化指数n呈明显的相关性。当n=0.45时,无论hf/hm为多大,测试误差不超过5%;当hf/hm<0.7时,不论n为多大,测试误差不超过5%;当hf/hm>0.7且n=0或n=0.15时,Oliver-Pharr方法计算的折合弹性模量显著大于真值;当hf/hm接近1时,其折合弹性模量最大测试误差将近32%。
考察其原因,BOLSHAKOV和PHARR[17]以及CHENG等[13]指出,这是由于压入低硬化水平材料且hf/hm较大时,压头周围材料的鼓凸现象所导致(见图5),此时真实接触深度hCM大于压入深度。Oliver-Pharr方法估算的接触深度总是小于压入深度,当压入凸起变形明显时,Oliver-Pharr方法所计算的投影接触面积明显小于真实接触面积,从而导致弹性模量的高估。

图5 压入测试中的鼓凸现象
Fig. 5 Illustration of pile-up in nanoindentation test
3 改进方法及其测试精度分析
由以上分析可知,当hf/hm>0.7且n比较小时,Oliver-Pharr方法计算的接触深度会明显小于真实接触深度,导致弹性模量计算结果高于真值较多。为此,通过对图4显示的折合弹性模量误差分布进行分析,引入下式对接触深度的计算进行修正
 (14)
(14)
应用修正后的接触深度重新计算折合弹性模量,以ErM表示,和真实折合弹性模量Er进行比较,令
 (15)
(15)
δrM随hf/hm和n的变化情况如图6所示。由图6可看出,对接触深度进行修正后,当hf/hm>0.7且n=0时,计算得到的折合弹性模量最大误差不超过15%,远小于修正前最大32%的误差;当hf/hm>0.7且n= 0.15时,计算得到的折合弹性模量误差值也有较大降低;对于hf/hm<0.7的情况,误差基本未变。当然,当hf/hm>0.7且n=0.45时,修正后计算得到的弹性模量最大误差接近±15%,超过对接触深度修正前的误差。但由于在压入测试中,材料的硬化指数仅靠压入载荷—深度数据是不可能预测的,因此,无法判断n的值,也就无法估计测量误差。为此,采用修正接触深度后的办法将hf/hm>0.7时,整体误差带下移,从而使最大测试误差控制在±15%以内,更适合于工程应用。

图6 误差δrM随hf/hm和n的变化
Fig. 6 Plots of δrM changing with hf/hm and n
4 实验结果
利用文献[18]发表的纳米压入实验数据来检验本研究提到的两种测试方法的精度。测试材料为两种铝合金,6061-T6511和7075-T651。它们的弹性模量通过单轴拉伸试验被确定为66.8 GPa和70.1 GPa。实验对每种材料固定最大载荷并且重复6次实施压入测试。金刚石压头的弹性模量为Ei=1 141 GPa,泊松比νi=0.07,两种被测材料的泊松比νi均为0.33。
分别应用Oliver-Pharr方法和改进方法识别被测材料的弹性模量,以EO-P和 EM表示,结果见表1和2。为方便分析,将表中测试结果和已知值进行了比较,列出了两种方法的测试误差。
由表1和2可以看出,利用Oliver-Pharr方法确定的6061-T651和7075-T651两种铝合金弹性模量均值分别为78.5 GPa和79.2 GPa,误差分别为17.5%和13.0%。由前面分析可知,造成误差较大的原因是其硬化指数较小(分别为0.08和0.122);且hf/hm较大,均大于0.8。而由改进方法确定的弹性模量均值分别为71.6 GPa和74.1 GPa,误差分别为7.2%和5.7%,测试误差明显减小。
表1 用Oliver-Pharr方法和改进方法识别铝合金6061-T6511的弹性模量
Table 1 Elastic modulus of Al 6061-T6511 obtained by Oliver-Pharr method and modified method

表2 用Oliver-Pharr方法和改进方法识别铝合金7075-T651的弹性模量
Table 2 Elastic modulus of Al 7075-T651 obtained by Oliver-Pharr method and modified method

5 结论
针对Oliver-Pharr方法在识别低硬化水平材料弹性模量时误差较大的问题,提出一种改进的纳米压入测试方法,改进方法对压入接触深度进行了重新估算,有限元分析和实验结果表明,应用改进方法确定材料折合弹性模量时最大误差可控制在±15%以内,远小于Oliver-Pharr方法最大近32%的误差。
REFERENCES
[1] ISO 14577. Metallic Materials-Instrumented Indentation Test for Hardness and Materials Parameter[S].
[2] 张泰华. 微/纳米力学测试技术及其应用[M]. 北京: 机械工业出版社, 2004: 4-6.
ZHANG Tai-hua. Test technology and applications of micro/nano-mechanics[M]. Beijing: China Machine Press, 2004: 4-6.
[3] 任明星, 李邦盛, 杨 闯, 傅恒志. 纳米压痕法测定微铸件硬度及弹性模量[J]. 中国有色金属学报, 2008, 18(2): 231-236.
REN Ming-xing, LI Bang-sheng, YANG Chuang, FU Heng-zhi. Hardness and elastic modulus of microcastings by nanoindentation[J]. The Chinese Journal of Nonferrous Metals, 2008, 18(2): 231-236.
[4] DOERNER F M, NIX W D. A method for interpreting the data from depth-sensing indentation instruments[J]. Journal of Materials Research, 1986, 1(4): 601-609。
[5] CAO Y, QIAN X, LU J, YAO Z. An energy-based method to extract plastic properties of metal materials from conical indentation tests[J]. Journal of Materials Research, 2005, 20(5): 1194-1198。
[6] CHENG Y T, CHENG C M. Scaling approach to conical indentation in elastic-plastic solids with work hardening[J]. J Appl Phys, 1998, 84(3): 1284-1291.
[7] 马德军. 材料弹性模量的仪器化压入测试方法[J]. 中国有色金属学报, 2010, 20(12): 2336-2343.
MA De-jun. Method for determining elastic modulus by instrumented indentation test[J]. The Chinese Journal of Nonferrous Metals, 2010, 20(12): 2336-2343.
[8] OLIVER W C, PHARR G M. An improved technique for determining hardness and elastic-modulus using load and displacement sensing indentation experiments[J]. Journal of Materials Research, 1992, 7(6): 1564-1583.
[9] OLIVER W C, PHARR G M. Measurement of hardness and elastic modulus by instrumented indentation: Advances in understanding and refinements to methodology[J]. Journal of Materials Research, 2004, 19(1): 3-20.
[10] HEY J L, PHARR G M. Instrumented indentation testing[M]. Ohio: ASM International, Materials Park. 2000: 232-243.
[11] BOLSHAKOV A, PHARR G M. Influences of stress on the measurement of mechanical properties using nanoindentation: Part Ⅱ. Finite element simulations[J]. Journal of Materials Research, 1996, 11(3): 760-768.
[12] PELLETIER H, KRIER J, CORNET A, MILLE P. Limits of using bilinear stress-strain curve for finite element modeling of nanoindentation response on bulk materials[J]. Thin Solid Films, 2000, 379(1/2): 147-155.
[13] CHENG Y T, CHENG C M. Scaling approach to conical indentation in elastic-plastic solids with work hardening[J]. J Appl Phys, 1998, 84(4): 1284-1291.
[14] LICHINCHI M, LENARDI C, HAUPT J, VITALI R. Simulation of Berkovich nanoindentation experiments on thin films using finite element method[J]. Thin Solid Films, 1998, 312(1/2): 240-248.
[15] MA De-jun, ZHANG Tai-hua, CHUNG W O. Evaluation of the effectiveness of representative methods for determining Young’s modulus and hardness from instrumented indentation data[J]. Journal of Materials Research, 2006, 21(1): 225-233.
[16] JOHUSON K L. Contact Mechanics[M]. Cambridge, UK: Cambridge University Press, 1985
[17] BOLSHAKOV A, PHARR G M. Influences of pile-up on the measurement of mechanical properties by load and depth sensing indentation techniques[J]. Journal of Materials Research, 1998, 13(4): 1049-1058.
[18] DAO M, CHOLLACOOP N, van VLIET K J, VENKATESH T A, SURESH S. Computational modeling of the forward and reverse problems in instrumented sharp indentation[J]. Acta Materialia, 2001, 49(19): 3899-3918.
(编辑 李艳红)
基金项目:国家自然科学基金资助项目(10672185)
收稿日期:2011-01-19;修订日期:2011-05-16
通信作者:宋仲康,讲师;电话:010-66717048;E-mail: song2004cn@yahoo.com.cn