土钉墙支护极限高度的有限元分析与拟合
俞建霖1,何萌1,张文龙1, 2,龚晓南1,应建新3
(1. 浙江大学 软弱土与环境土工教育部重点实验室,浙江 杭州,310058;
2. 上海现代建筑设计集团 申元岩土工程有限公司,上海,200011;
3. 浙江世贸房地产开发有限公司,浙江 杭州,310007)
摘要:利用地基极限承载力的有限元分析法求解思路分析基坑工程中土钉墙支护的极限高度,研究土钉墙支护的主要影响因素与极限高度之间的变化规律,具体包括地基土体黏聚力、内摩擦角、土钉长度、边坡坡角、地基土体弹性模量和复合土体弹性模量等因素。通过拟合分析方法,重点考虑地基土体黏聚力、内摩擦角、土钉长度、边坡坡角4个主要因素,提出计算土钉墙支护极限高度的经验公式,该公式在垂直开挖无支护情况下即为无支护下竖直陡坡的临界高度理论解。通过2个工程实例分析,证明了采用经验公式的计算结果与工程实际情况比较吻合,对基坑工程的设计和分析具有借鉴和参考价值。
关键词:土钉墙支护;极限高度;增量有限元法;影响因素;拟合公式
中图分类号:TU46+3 文献标志码:A 文章编号:1672-7207(2011)05-1447-07
Finite element analysis and fitting of critical height of soil nailed wall
YU Jian-lin1, HE Meng1, ZHANG Wen-long1, 2, GONG Xiao-nan1, YING Jian-xin3
(1. Key Laboratory of Soft Soils and Geoenvironmental Engineering of Ministry of Education,
Zhejiang University, Hangzhou 310058, China;
2. Xiandai Architectural Design Group, Shen Yuan Geotechnical Engineering Co.,Ltd, Shanghai 200011, China;
3. Zhejiang Shimao Real Estate Development Co. Ltd., Hangzhou 310007, China)
Abstract: Using the thought of finite element of ultimate bearing capacity of foundation, the critical height of soil nailed wall foundation pit was analyzed. The laws between the critical height and the chief influence factors including the cohesion of soil, the internal friction angle of soil, the soil nail length, the slope angle, the elastic modulus of soil, the elastic modulus of composite soil were studied, then through the fitting analysis, the empirical formulas of the critical height of soil nailing foundation pit was simulated, considering four chief influence factors which were the cohesion of soil, the internal friction angle, the soil nail length and the slope angle. This formula was the theoretical solution of critical height of unsupported upright slope when the foundation pit was upright excavated under the condition of unsupported. The case analysis verifies the results and shows that the empirical formulas can fit the engineering projects very well, which can provide reference value for the design and the analysis of foundation pit.
Key words: soil nailed wall; critical height; step loading finite element method; influential factor; fitting formula
采用土钉墙支护的基坑和边坡,往往具有较好的经济技术效果。土钉墙支护后土体强度提高或者土钉墙支护边坡的自稳性增加,其作用机理在于土钉与土之间的相互摩擦联结之中,使土钉对复合土体发挥骨架约束作用、分担作用、应力的传递与扩散作用以及对坡面变形的约束作用等[1]。在许多软土地区对土钉墙支护的基坑开挖深度有严格的限制,甚至许多规程均注明土钉墙支护不适用于软黏土地基中基坑支 护[2-4],但在沿海地区的浙江、上海和福建等地的软土地基中成功应用土钉墙支护的工程实例已经有很 多[5-10]。然而,在软土地基采用土钉墙支护的基坑中发生事故、产生整体失稳的工程也占有相当大的比例。为了安全、经济地进行基坑土钉墙支护结构的设计,为设计人员提供必要的设计依据,土钉墙支护的极限高度问题日益引起人们的重视。软土地基中基坑开挖深度超过土钉墙支护的极限高度往往引起基坑隆起,导致深层整体失稳破坏,而且软土地基中土钉墙支护破坏大多数属于这种情况。这既是一个设计理论的问题,也是一个实际工程问题。要准确解决土钉支护极限高度的问题,目前尚有困难。如果能够确定出极限高度的计算方法,不但能够大大拓展土钉墙支护的应用范围,还能够充分发挥土钉墙支护的围护作用,大大提高经济效益。目前,国内外学者对土钉墙支护极限高度的研究比较少。龚晓南[11]认为在基坑土钉墙支护中,通过加密土钉,可以防止最危险圆弧滑动面从土钉加固体中穿过,即保证其内部稳定性;但是,当基坑底部土体不能承受上部土体重力而产生破坏时,再加密加长土钉也无济于事,此时基坑往往产生深层整体失稳破坏:基坑内侧土体产生隆起,而基坑外侧土体产生下陷。因此,土钉墙支护的极限高度与基坑底部土层的承载力有密切关系,通过分析基坑底部土层的承载力可以得到土钉墙支护的极限高度。因此,在本文中主要通过分析地基的整体稳定性(即外部整体稳定性)来讨论土钉墙支护的极限高度,而对于土钉锚固力不足引起的土钉墙破坏则可通过加长、加密土钉等措施来改善。地基承载力可以采用极限分析法的上下限定理来求解。当前采用的经典极限分析法包括:极限平衡法、滑移线场法、上、下限分析法与变分法。各种方法有各自的优缺点,有些还要进行一定的假定,从而使极限分析法的应用受到限制。极限分析有限元法弥补了上述不足,并具有有限元法的一切优点,不但考虑了变形,而且可以对施工过程进行动态模拟。极限分析有限元法在分析边坡稳定性可以直接求出安全系数以及临界滑动面,在边坡支挡结构的设计中,既可以考虑支护结构与岩土介质共同作用关系,而且可以直接算出结构内力,从而扩大了极限分析法的应用范围[12]。在此,本文作者利用ANSYS软件来模拟基坑开挖与土钉的施工过程,通过变化各种参数可以得出土钉墙支护极限高度的变化规律;根据分析结果并结合工程实际,选取了主要影响因素,拟合出土钉墙支护极限高度与各个主要影响因素间的关系式,进而提出土钉墙支护极限高度经验公式,并通过工程实例对该公式进行验证。
1 有限元模型建立
本文主要通过分析地基的整体稳定性来讨论土钉墙支护的极限高度,同时,由于地基土体经土钉加固后强度得到了较大提高,在一般情况下,在软土地基中土钉墙支护破坏时其滑动面往往在土钉加固区以外。因此,本文将土钉和经喷浆加固的土体作为复合土体来进行分析,进而求解地基的极限承载力。
根据邓楚键等[13]提出采用增量加载的方法求解地基极限承载力的思路,随着荷载的逐步增加,岩土体由弹性逐渐过渡到塑性,最后达到极限状态,这时对应的荷载就为所要求的极限荷载,而此时对应的开挖高度就是土钉墙支护的极限高度。本文采用的ANSYS有限元软件,通过自动荷载步长加载技术就可方便地实现这一加载求解过程,并且在增量施加开挖荷载的过程中,可以分析每一步施加开挖荷载后土钉墙支护的性状。
屈服准则采用Mohr-Coulomb不等角六边形外接圆D-P屈服准则。郑颖人等[12]研究表明,采用该准则与传统Mohr-Coulomb屈服准则的计算结果有较大误差。为了与传统工程中Mohr-Coulomb准则条件下的安全系数(或者极限承载力)接轨,提出对于平面应变条件下的强度问题,可采用与传统Mohr-Coulomb准则相匹配的D-P准则。采用关联流动法则时(膨胀角 等于内摩擦角
等于内摩擦角 ),
),
 ,
, (1)
(1)
本文即采用此种方法。
基坑破坏后由稳定状态转变为运动状态,滑体出现无限移动,此时,滑移面上出现塑性应变或者位移出现突变;此外,有限元计算会同时出现计算不收敛,在突变前计算收敛,突变之后计算不收敛。
采用杀死单元和替换单元材料来分别模拟基坑的开挖过程和土钉的施工过程。土体自重荷载一次性施加,将开挖荷载以等效节点力的形式反加于开挖节点处。本文采用Ghaboussi等[14]提出的方法计算开挖等效荷载,用下式表示:
 (2)
(2)
式中:{F}为j阶段的开挖荷载;{B}为应变位移矩阵;Vj为j阶段开挖土体的体积; 为当前土体应力;[N]为单元形函数;
为当前土体应力;[N]为单元形函数; 为土体重度。
为土体重度。
有限元计算模型如图1所示。同时,在建模和计算过程中采用以下基本假定:
(1) 基坑土钉墙支护按平面应变问题进行分析。
(2) 土体视为各向同性弹塑性均质体。
(3) 地基土体、土钉和土形成的复合土体均采用平面4节点等参单元。
(4) 模型左侧与右侧的边界条件均为ux=0,模型底部的边界条件为ux=uy=0。
计算模型的计算域宽度B=60 m,高度H=21 m,基坑开挖宽度Le=30 m,边坡坡角 =90°,土钉长度Ln=10 m。地基土体重度γs=17.7 kN/m3,内摩擦角φs=10.2°,黏聚力cs=15.8 kPa,弹性模量Es=2 MPa,泊松比μs=0.45。复合土体重度γc=19.0 kN/m3,内摩擦角φc=20.4°,黏聚力cc=37.5 kPa,弹性模量Ec=28 MPa,泊松比μc=0.32。以上参数值作为整个计算过程的基本值,每步开挖高度为0.5 m。
=90°,土钉长度Ln=10 m。地基土体重度γs=17.7 kN/m3,内摩擦角φs=10.2°,黏聚力cs=15.8 kPa,弹性模量Es=2 MPa,泊松比μs=0.45。复合土体重度γc=19.0 kN/m3,内摩擦角φc=20.4°,黏聚力cc=37.5 kPa,弹性模量Ec=28 MPa,泊松比μc=0.32。以上参数值作为整个计算过程的基本值,每步开挖高度为0.5 m。

图1 有限元分析网格图
Fig.1 Finite element analysis grid chart
本文把按照以上各原始参数进行计算的算例称为土钉墙支护的标准算例,选定竖直开挖面坡脚处水平位移发生突变来作为基坑发生破坏的标志,此时,对应的基坑开挖深度即为土钉墙支护的极限高度。
2 土钉墙支护极限高度影响因素分析
为了分析土钉墙支护极限高度的影响因素和变化规律,在标准算例的基础上分别变化单个参数而其他参数保持不变,从而得出土钉墙支护极限高度的变化规律,并拟合出土钉墙支护极限高度与各主要影响因素的关系式。
2.1 土体黏聚力的影响
分别计算地基土体黏聚力cs为4,8,12,16,20和24 kPa 6种情况。图2所示为地基土体黏聚力对土钉墙支护极限高度的影响。由图2可见:随着地基土体黏聚力的增大,土钉墙支护的极限高度也显著增大,说明地基土体的性质对土钉墙支护的极限高度有较大影响。
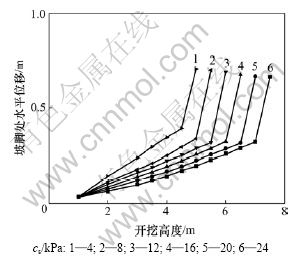
图2 地基土体黏聚力与坡脚处水平位移关系图
Fig.2 Relationship between cohesion of soil and horizontal displacement of toe of slope
土钉墙支护极限高度与土体黏聚力关系如图3所示。由图3可见:土钉墙支护极限高度与地基土体黏聚力二者之间存在着近似线性的关系。

图3 土钉墙支护极限高度与土体黏聚力关系图
Fig.3 Relationship between cohesion of soil and critical height of soil nailed wall
2.2 土体内摩擦角的影响
分别计算土体内摩擦角φs为5?,10?,20°,30°和40°对土钉墙支护极限高度的影响,结果见图4。由图4可以看出:地基土体内摩擦角对土钉墙支护极限高度也有显著的影响:随着土体内摩擦角的增大,土钉墙支护的极限高度显著提高。

图4 土体内摩擦角与坡脚处水平位移关系图
Fig.4 Relationship between angle of internal friction of soil and horizontal displacement of toe of slope
土钉墙支护极限高度与土体内摩擦角关系如图5所示。由图5可见:土钉墙支护极限高度和 tan (45o+φs/2)之间也存在着近似线性的关系。

图5 土钉墙支护极限高度与土体内摩擦角关系图
Fig.5 Relationship between angle of internal friction of soil and critical height of soil nailed wall
2.3 土钉长度的影响
分别计算土钉长度Ln为0,1,5,10,15和20 m对土钉墙支护极限高度的影响,结果见图6。由图6可以看出:在一定范围增加土钉长度可以提高土钉墙支护的极限高度,但增长的幅度逐渐减小;当土钉长度增加到某临界值后,土钉墙支护的极限高度几乎没有变化,说明土钉长度对土钉墙支护的极限高度的影响是有一定限度的。
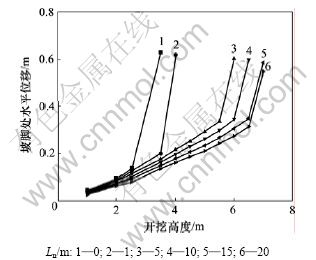
图6 土钉长度与坡脚处水平位移关系图
Fig.6 Relationship between length of soil nail and horizontal displacement of toe of slope
土钉墙支护极限高度与土钉长度关系曲线见图7。由图7可见:土钉长度对极限高度的影响存在着一定的临界值,可采用双曲线关系式来拟合土钉墙支护极限高度和土钉长度之间的关系:
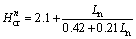 (3)
(3)
式中: 为土钉墙支护下极限高度(m);Ln为土钉长度(m)。
为土钉墙支护下极限高度(m);Ln为土钉长度(m)。

图7 土钉墙支护极限高度与土钉长度关系曲线图
Fig.7 Relationship between length of soil nail and critical height of soil nailed wall
2.4 边坡坡角的影响
在实际的工程应用中,由于施工以及场地等多方面的原因,边坡坡角一般控制在30°~90°之间。分别计算边坡坡角 为35°,45°,55°,63°和90°(对应坡度分别为1:1.5,1:1,1:0.7,1:0.5以及垂直放坡)5种情况。图8所示为边坡坡角对土钉墙支护极限高度的影响。由图8可以看出:边坡坡角对基坑坡脚处水平位移的影响比较明显:随着边坡坡角的增大,土钉墙支护极限高度逐渐减小。
为35°,45°,55°,63°和90°(对应坡度分别为1:1.5,1:1,1:0.7,1:0.5以及垂直放坡)5种情况。图8所示为边坡坡角对土钉墙支护极限高度的影响。由图8可以看出:边坡坡角对基坑坡脚处水平位移的影响比较明显:随着边坡坡角的增大,土钉墙支护极限高度逐渐减小。
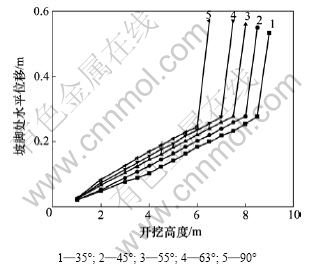
图8 边坡坡角与坡脚处水平位移关系图
Fig.8 Relationship between slope angle and horizontal displacement of toe of slope
土钉墙支护下极限高度与边坡坡角关系曲线见图9。由图9可见:土钉墙支护极限高度和边坡坡角(弧度值)之间呈线性递减的关系。
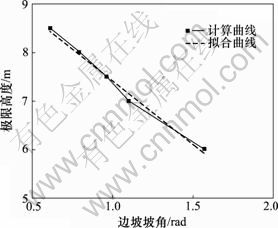
图9 土钉墙支护极限高度与边坡坡角关系曲线图
Fig.9 Relationship between slope angle and critical height of soil nailed wall
2.5 地基土体弹性模量的影响
图10所示为地基土体弹性模量对土钉墙支护极限高度的影响。由图10可以看出:地基土体弹性模量对坡脚处水平位移和土钉墙支护的极限高度影响较大;随着地基土体弹性模量的增大,土钉墙支护极限高度也逐步增大。

图10 土体弹性模量与坡脚处水平位移关系图
Fig.10 Relationship between elastic modulus of soil and horizontal displacement of toe of slope
2.6 复合土体弹性模量的影响
复合土体弹性模量与坡脚处水平位移关系见图11。由图11可以看出:当土钉加固区范围内的复合土体弹性模量较小时,提高复合土体的弹性模量可以逐步增大土钉墙支护的极限高度;但是,当复合土体弹性模量增大到一定值时,再提高其值对土钉墙支护的
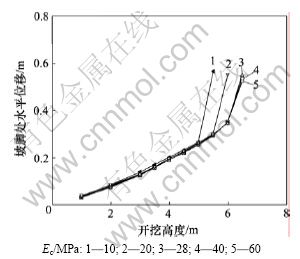
图11 复合土体弹性模量与坡脚处水平位移关系图
Fig.11 Relationship between elastic modulus of composite soil and horizontal displacement of toe of slope
极限高度几乎没有影响,说明通过提高土钉密度和增加注浆量来增大复合土体模量,从而提高土钉墙支护极限高度的能力也是有一定限度的。
3 土钉墙支护极限高度拟合分析
为了进一步揭示土钉墙支护下各个不同影响因素对极限高度的变化规律,并结合工程实际,由于地基土体弹性模量与内摩擦角、黏聚力之间存在着很大的相关性,而复合土体弹性模量增大到一定范围后对土钉墙支护极限高度影响很小,因此,这里考虑地基土黏聚力、内摩擦角、土钉长度和边坡坡角4个主要因素的影响,经归纳并考虑量纲前后对应,假定土钉墙支护极限高度的计算式形式如下:
 (4)
(4)
式中:a1,a2,a3和a4为待定参数。
由式(4),将基本算例中参数值代入进行分析计算得出各待定参数值,最后可得到土钉墙支护极限高度的计算公式如下:

 (5)
(5)
式中:Pa为标准大气压,等于1×105 Pa;cs为土体黏聚力(kPa);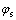 为土体内摩擦角(°);γs为土体重度(kN/m3);Ln为土钉长度(m);
为土体内摩擦角(°);γs为土体重度(kN/m3);Ln为土钉长度(m);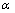 为边坡坡角(rad);并取π/6≤
为边坡坡角(rad);并取π/6≤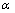 ≤π/2。当Ln=0,
≤π/2。当Ln=0,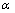 =π/2,即垂直开挖无支护时,将相应参数代入式(5),式(5)便成为
=π/2,即垂直开挖无支护时,将相应参数代入式(5),式(5)便成为 ,等于无支护下竖直陡坡的临界高度的理论解[15]。
,等于无支护下竖直陡坡的临界高度的理论解[15]。
4 工程实例分析
为了验证土钉墙支护极限高度计算公式的适用性,选用2个工程实例来进行验证。
(1) 工程实例一:该工程位于杭州城西软土地基中,设计基坑开挖深度为6.7 m,采用5排土钉墙支护,土钉长度为15 m,边坡坡度为65°,基坑开挖深度内各土层物理力学参数见表1。
表1 工程实例一中各土层物理力学参数表
Table 1 Physical and mechanical parameter list of soils of engineering example one
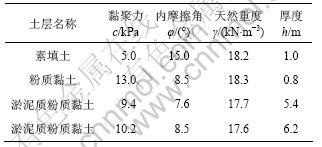
由于式(5)中未包括成层土的情况,为便于计算,根据表1中各个土层的物理力学参数和厚度,采用加权平均的方法获得计算参数,加权的土层总厚度取开挖深度的2倍。由此可得计算参数如下:cs=9.66 kPa,φs=8.6°,γs=17.8 kN/m3,土钉长度Ln=15 m,坡体放坡角度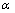 =65°。
=65°。
代入式(5)进行计算,可得到土钉墙支护极限高度 =6.26 m,小于该基坑的设计开挖深度6.7 m。实际施工中基坑开挖深度达到6.2 m左右时该基坑发生整体失稳破坏,与用本文公式计算的支护极限高度6.26 m是比较接近的。
=6.26 m,小于该基坑的设计开挖深度6.7 m。实际施工中基坑开挖深度达到6.2 m左右时该基坑发生整体失稳破坏,与用本文公式计算的支护极限高度6.26 m是比较接近的。
(2) 工程实例二:该工程位于杭州城东砂性土地基,地下室为2层。基坑开挖深度为7.6 m,采用土钉墙支护,土钉长度为10 m,边坡坡度为60°,并且在基坑开挖过程中进行了降水。基坑开挖深度影响范围内各土层物理力学参数见表2。
表2 工程实例二中各土层物理力学参数表
Table 2 Physical and mechanical parameter list of soils of engineering example two
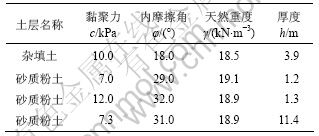
采用相同的计算方法,各计算参数如下:cs=8.4 kPa,φs=27.6°,γs=18.8 kN/m3,土钉长度Ln=10 m,坡体放坡角度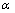 =60°。
=60°。
代入式(5)进行计算,可得到土钉墙支护极限高度 =8.03 m,大于该基坑的设计开挖深度7.6 m,本工程的实际土钉墙支护深度亦为7.60 m,实际的支护高度在公式计算的极限高度范围内。观测结果表明:基坑周边土体的侧向位移较小,基坑处于安全状态。
=8.03 m,大于该基坑的设计开挖深度7.6 m,本工程的实际土钉墙支护深度亦为7.60 m,实际的支护高度在公式计算的极限高度范围内。观测结果表明:基坑周边土体的侧向位移较小,基坑处于安全状态。
5 结论
(1) 在一定范围增加土钉长度可以提高土钉墙支护的极限高度;但土钉长度增加到一定程度后,其支护极限高度几乎不再变化,说明单纯依靠增加土钉长度来提高土钉墙支护的极限高度有一定的限度。
(2) 当复合土体弹性模量提高到一定值的时 候,再提高复合土体的弹性模量对土钉墙支护的极限高度几乎没有影响,说明单纯依靠提高土钉密度和增加注浆量来提高土钉墙支护的极限高度也是有一定限度的。
(3) 随着土体黏聚力、土体内摩擦角、土体弹性模量、复合土体弹性模量的提高,土钉墙支护极限高度逐步提高;随着坡体放坡角度增加,土钉墙支护极限高度逐步减小。
(4) 通过拟合分析提出了土钉墙支护极限高度的经验公式,当垂直开挖无支护时,用该公式所得解正好等于无支护下竖直陡坡的临界高度理论解。并通过工程实例进行验证,结果比较吻合。
(5) 本文提出的土钉墙支护极限高度的计算公式未考虑地基土体分层和复合土钉墙支护的情况,对上述2种情况下土钉墙支护的极限高度尚需进一步研究。
参考文献:
[1] 张旭辉. 锚管桩复合土钉支护稳定性研究[D]. 杭州: 浙江大学建筑工程学院, 2002: 24-25.
ZHANG XU-hui. Stability of channel-steel-piles composite soil nailing[D]. Hangzhou: Zhejiang University. College of Civil Engineering and Architecture, 2002: 24-25.
[2] CECS 96—97. 基坑土钉墙支护技术规程[S].
CECS 96—97. Specification for soil nailing in foundation excavations[S].
[3] JGJ 120—99. 建筑基坑支护技术规程[S].
JGJ 120—99. Technical specification for retaining and protection of building foundation excavations[S].
[4] YB 9258—97. 建筑基坑工程技术规程[S].
YB 9258—97. Technical specifications for foundation pits excavation for buildings[S].
[5] 吴铭炳. 软土基坑土钉墙支护的理论与实践[J]. 工程勘察, 2000(3): 40-43.
WU Ming-bing. The theory and practice of soil nailing bracing in foundation pit of soft soil[J]. Geotechnical Investigation & Surveying, 2000(3): 40-43.
[6] 梁勇彪, 徐霞琴. 土钉支护在极软土基坑工程中的应用[J]. 岩土工程师, 2003, 15(3): 42-43.
LIANG Yong-biao, XU Xia-qin. Application of soil nailing in excavation of soft ground[J]. Geotechnical Engineer, 2003, 15(3): 42-43.
[7] 张晁, 郑俊杰, 辛凯. 土钉墙支护技术在软土基坑中的应用[J]. 岩石力学与工程学报, 2002, 21(6): 923-925.
ZHANG Chao, ZHENG Jun-jie, XIN Kai. Application of soil nail technique in soft soil foundation pit[J]. Chinese Journal of Rock Mechanics and Engineering, 2002, 21(6): 923-925.
[8] 吴铭炳. 软土地基土钉支护研究[J]. 岩土工程学报, 1999, 21(6): 687-690.
WU Ming-bing. The study for soil nailing in soft clay foundation excavation[J]. Chinese Journal of Geotechnical Engineering, 1999, 21(6): 687-690.
[9] 陈肇元, 崔京浩. 土钉支护在基坑工程中的应用[M]. 北京: 中国建筑工业出版社, 1997: 64-67.
CHEN Zhao-yuan, CUI Jing-hao. Application of soil nailing supported in excavation[M]. Beijing: China Architecture & Building Press, 1997: 64-67.
[10] 庞晓明, 沈水龙, 许烨霜. 复合土钉支护基坑的工程实例分析[J]. 岩土工程学报, 2006, 28(增刊): 1838-1841.
PANG Xiao-ming, SHEN Shui-long, XU Ye-shuang. Analysis of behavior of nailing supported mixed soil-cement wall in excavation[J]. Chinese Journal of Geotechnical Engineering, 2006, 28(Supp.): 1838-1841.
[11] 龚晓南. 土钉和复合土钉墙支护若干问题[J]. 土木工程学报, 2003, 36(10): 80-83.
GONG Xiao-nan. Some problems on soil nailing and composite soil nailing[J]. China Civil Engineering Journal, 2003, 36(10): 80-83.
[12] 郑颖人, 赵尚毅. 岩土工程极限分析有限元法及其应用[J]. 土木工程学报, 2005, 38(1): 91-98.
ZHENG Ying-ren, ZHAO Shang-yi. Limit state finite element method for geotechnical engineering analysis and its applications[J]. China Civil Engineering Journal, 2005, 38(1): 91-98.
[13] 邓楚键, 孔位学, 郑颖人. 极限分析有限元法讲座Ⅲ—增量加载有限元法求解地基承载力[J]. 岩土力学, 2005, 26(3): 500-504.
DENG Chu-jian, KONG Wei-xue, ZHENG Ying-ren. Analysis of ultimate bearing capacity of foundations by elastoplastic FEM through step loading[J]. Rock and Soil Mechanics, 2005, 26(3): 500-504.
[14] Ghaboussi J, Pecknold D A. Incremental finite analysis of geometrically altered structures[J]. International Journal for Numerical Methods in Engineering, 1984, 20(11): 2051-2064.
[15] 龚晓南.土塑性力学[M]. 2版. 杭州: 浙江大学出版社, 1999: 343-344.
GONG Xiao-nan. Soil plasticity[M]. 2nd ed. Hangzhou: Zhejiang University Press, 1999: 343-344.
(编辑 杨幼平)
收稿日期:2010-03-10;修回日期:2010-06-15
基金项目:浙江省建设厅基金资助项目(08Z009)
通信作者:俞建霖(1972-),男,福建福清人,博士,副教授,从事软黏土力学、基坑工程、地基处理及土工数值分析的研究;电话:13906525721;E-mail: yujianlin72@126.com