Trans. Nonferrous Met. Soc. China 25(2015) 3240-3246

Effect of indentation size and grain/sub-grain size on microhardness of high purity tungsten

Guang-yu LIU, Song NI, Min SONG

State Key Laboratory of Powder Metallurgy, Central South University, Changsha 410083, China

Received 29 January 2015; accepted 13 May 2015

Abstract: Hardness of materials depends significantly on the indentation size and grain/sub-grain size via microindentation and nanoindentation tests of high-purity tungsten with different structures. The grain boundary effect and indentation size effect were explored. The indentation hardness was fitted using the Nix-Gao model by considering the scaling factor. The results show that the scaling factor is barely correlated with the grain/sub-grain size. The interaction between the plastically deformed zone (PDZ) boundary and the grain/sub-grain boundary is believed to be the reason that leads to an increase of the measured hardness at the specific depths. Results also indicate that the area of the PDZ is barely correlated with the grain/sub-grain size, and the indentation hardness starts to stabilize once the PDZ expands to the dimension of an individual grain/sub-grain.

Key words: high purity tungsten; indentation hardness; indentation size effect; grain boundary; plastic deformation zone

1 Introduction

Indentation tests have widely been used as an effective and economical method for measuring the mechanical properties of materials, including hardness and elastic modulus [1], elastic properties [2] and creep properties [3,4]. It has well been recognized that indentation hardness depends significantly on the indentation size or depth [5-12]. This phenomenon is referred to the indentation size effect (ISE) and is attributed to the evolution of geometrically necessary dislocations (GNDs) beneath the indenter, which gives rise to the strain gradients [13,14]. The plastically deformed zone (PDZ) and its evolution that are correlated to the hardness values were widely investigated [15-17].

In last several decades, many explanations have been proposed to describe the ISE, including the presence of oxides or chemical contamination near the surfaces [18], characteristic size plastic deformation [19] and a critical thickness layer [20]. Among all the explanations, Nix-Gao model [21] based on GNDs and Taylor dislocation model [22] might be the most important one, which can be expressed as

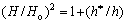                       (1)

where H is the real hardness, H_o is generally called the macroscopic hardness, corresponding to the hardness that results from statistically stored dislocations (SSDs) in the absence of GNDs, and is always obtained when the indentation depth (h) becomes infinitely large; h^* is a characteristic length that characterizes the dependence of the hardness on the indentation depth [23]. It is suggested that in the Nix-Gao model the total dislocation density represents the total coupling between GNDs and SSDs, both of which play a significant role in the hardening mechanism. Although the Nix-Gao model could certainly agree well with many experimental results [21], some nanoindentation results [24-26] showed that it cannot predict the hardness with a small indentation size/depth precisely. FENG and NIX [25] suggested that the Nix-Gao model overestimated the hardness of MgO for small indentation and pointed out that it might be caused by a slight expansion of the PDZ [25]. It should be noted that the PDZ was not considered in the Nix-Gao model, in which the radius (a_pz) of the PDZ is regarded as the contact radius (a_c) between the indenter and the materials. DURST et al [24] also indicated that plastically deformed volume used to store the GNDs is larger than the volume defined in the Nix-Gao model, and they proposed a correction by considering the ISE, in which the radius of the PDZ is calculated by a_pz-fa_c approximately, where f is a factor dependent on the material. Moreover, ABU Al-Rub [27] formulated a micromechanical-based model that can be used to predict the ISE for both microindentation and nanoindentation simultaneously. This model is based on the evolution of GNDs beneath the indenter that is nonlinearly coupled (linearly coupled in the Nix-Gao model) with the evolution of SSDs through the Taylor’s hardening law. A couple of parameters, H_y and β, were introduced by ABU Al-Rub et al [27].

          (2)

where H_y is the hardness due to the initial yield stress (friction hardness) and β is considered as a material constant (interaction coefficient). β is normally used to assess the prediction sensitivity that the coupling between the SSDs and GNDs is enhanced during the plastic deformation process. It should be noted that if both SSDs and GNDs are coupled in a linear sense, i.e. β=2 and the friction hardness is neglected, i.e. H_y=0, the model of ABU Al-Rub et al [27] (Eq. (2)) returns to the commonly-used Nix-Gao model. However, all these models do not consider the interaction between the dislocations and grain boundaries, except for the work of YANG and VEHOFF [28], in which it was suggested that for large grains the hardness always decreases with increasing the indentation depth by using the nanoindentation tests in the center of individual grains to study the ISE and grain size effect (GSE). For small grains the hardness exhibited a behavior opposite to that of the coarse grains because of the grain boundary effect (GBE). In this work, the indentation hardness of high purity tungsten (W) with different structures was performed, in order to further understand the ISE and GBE during indentation.

2 Experimental

High purity W (99.95%) with two types of structures (fully dense coarse-grained structure and fine-grained structure with residue pores after sintering) was received from market and fabricated by using W powder with spark plasma sintering (SPS) technique at a sintering temperature of 1700 °C. All the specimens were mechanically polished by using emery paper and fine diamond (particle size of 0.5 μm) to meet the requirements for indentation tests using an ultra nano- (with effective radius of about 50-100 nm at the tip) and micro-indentation tester with Berkovich tips (with an effective radius of 100-200 nm at the tip). The indents were displacement/depth-controlled and the indentation hardness was obtained by Oliver and Pharr method [1]. Specifically, all the samples were pressed with the same penetrating rate of 5 nm/s to different maximum displacements, followed by holding at the maximum displacement for 10 s, and then the load was completely unloaded in 10 s. Three intents were tested for each process and the average value was used to plot the load-depth (p-h) curves and to calculate the indentation hardness. It should be noted that the W surface obtained through mechanical polishing is rather even. This can be well demonstrated by the fact that the p-h curves look the same as the depth increased (see Fig. 1). No electrolytic polishing was performed to remove the mechanical surface layer from the sample based on the following considerations. Firstly, even though the working hardened layers produced by mechanical polishing in W can lead to an increase in the hardness of the surface layer to some extent, the surface stress layer produced by friction between the W and the emery paper is extremely thin due to the high hardness of W [29]. Thus, the effect of surface stress and thin harder surface layer on the hardness was neglected in this work. Secondly, it is generally recognized that exposure to corrosive environments may form a chemically modified layer on the surface, which can influence the hardness if it is sufficiently thick [5]. To exclude this factor, only mechanical polishing without any electrolytic polishing was used to obtain the required surface. Macroscopic hardness of the full densification structured W was tested by using 500RMA hardness testing machine, and the microstructures were characterized by using a FEI Nova nano230 scanning electron microscope (SEM) and electron back-scattering diffraction (EBSD) technique in conjunction with SEM.

3 Results and discussion

Figure 1 shows the load-depth curves of the full densification structured W under nanoindentation and microindentation, respectively. The maximum depths for nanoindentation and microindentation are in the range from 50 to 600 nm (Fig. 1(a)) and from 600 to 5000 nm (Fig. 1(b)), respectively. It can be seen from Fig. 1 that the p-h curves appear to be the same with increasing the depth, particularly for microindentation (see Fig. 1(b)). Good repeatability of the p-h curves under the same indentation process validates the effectiveness of the experimental results. Most importantly, when more attention is paid to the very beginning of the p-h curve (rectangle section in Figs. 1(a) and (b)), it is found that no pop-in behavior was observed. It is generally recognized that the pop-in behavior at the beginning of the loading process is the result of the transition from elastic to plastic deformation and is attributed to the homogeneous nucleation of dislocations during indentation [30-32]. A distinct pop-in will be detected if indentation is performed on the perfectly prepared surfaces with a small number of dislocations and a high surface quality. Therefore, no pop-in behavior reveals that the mechanically polished surface of the W gives rise to some dislocations and may lead to a hardened surface layer, which would be one of the reasons for the higher hardness at the shallow indentation depth.

Figures 2(a) and (b) show the SEM and EBSD images of two areas for the full densification structured W. The line intercept method was used to measure the grain size and the results suggest that the average grain size is about 15 μm. EBSD observation shows that the grain/sub-grain has an inhomogeneous distribution with the size in the range from 3.5 (sub-grain size) to 15 μm (grain size). It should be noted that the grain boundaries observed in Fig. 2(a) are high angular boundaries with the misorientations being larger than 15°, instead of sub-grain boundaries with the misorientations smaller than 15°. This is because the grain boundaries with large misorientations are easier to be corroded by chemical etchant than sub-grain boundaries (small misorientations) due to the high free energy. Additionally, the EBSD image in Fig. 2(b) presents all the boundaries with the misorientations being larger than 3°. It should be noted that if the misorientation threshold is enlarged to 15° for the EBSD database, almost all the small-sized sub-grains in Fig. 2(b) will be vanished, indicating that most small-sized grains that are not observed in Fig. 2(a) are sub-grains. Figures 2(c) and (d) show the SEM images of the SPS-fabricated W sintered for 1 and 5 min, showing the average grain sizes of 3 and 4 μm, respectively. The W after SPS sintering for 1 and 5 min has obvious residue pores in the matrix, and the relative densities are 82.5% and 89.3%, respectively.

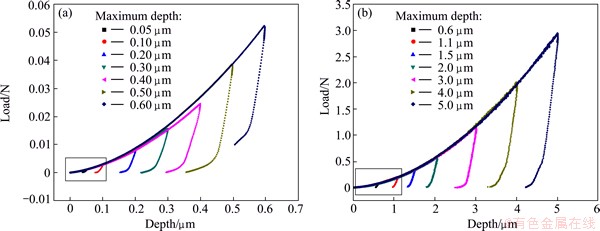
Fig. 1 Plots of load vs depth for fully dense W using nanoindentation (a) and microindentation (b)

Fig. 2 SEM (a) and EBSD (b) images of fully dense W, and SEM images of SPS fabricated W under sintering temperature of 1700 °C for 1 min (c) and 5 min (d), respectively

Figure 3 shows the hardness (H) as a function of the depth for the full densification structured W. It can be seen from Fig. 3(a) that the nanoindentation tested hardness shows a downward trend with increasing the depth from 50 to 600 nm. The fitted line (arrowed) obtained by using the Nix-Gao model in Fig. 3(a) gives the fitting parameters of 4.0 GPa for H_o and 270.1 nm for h^*. It is noted that 4.0 GPa is similar to the value obtained by macroscopic hardness testing results (3.95 GPa). The corresponding plot of H² versus 1/h shown as insert of Fig. 3(a) further reveals that a linear relation predicted by the Nix-Gao model agrees well with the experimental results for the indentation depth larger than 200 nm (1/h<0.005 nm^-1).

Fig. 3 Plots of indentation hardness vs depth tested for fully dense W using nanoindentation (a) and nanoindentation and microindentation (b)

Microindentation tests were also performed to further study the relationship between the hardness and indentation depth. The hardness obtained with the depth from 600 to 5000 nm is combined with the data in Fig. 3(a), as shown in Fig. 3(b). It can be seen that the hardness shows a relatively stable fluctuation around 5.0 GPa when the depth is larger than 2000 nm. Before that, there is a significant increase of the hardness from 4.6 GPa to a peak value of 5.3 GPa when the depth increases from 900 to 1100 nm. The Nix-Gao model marked by blue solid line (with the same H_o and h^* as Fig. 3(a)) reveals that this fitted line is consistent with the experimental data for h from 200 to 900 nm. It should be noted that the Nix-Gao model does not agree with the experimentally determined data at larger depth. The hardnesses obtained at a depth of 600 nm using both the nano-indenter and micro-indenter are extremely close, indicating that the indentation depth/size is the dominant factor affecting the hardness.

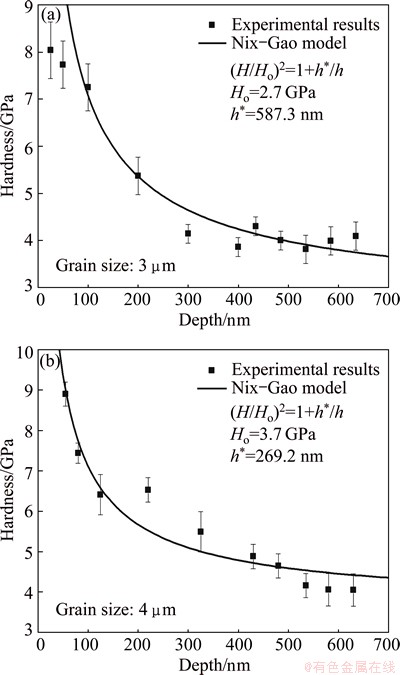
Fig. 4 Plots of indentation hardness vs depth tested using nanoindentation for SPS-fabricated W with grain size of 3 μm (a) and 4 μm (b)

Figures 4(a) and (b) show the hardness as a function of the depth for SPS-fabricated W with grain sizes of 3 and 4 μm, respectively. Figure 4(a) shows that the hardness has constant decline trend at the depth from 25 to 400 nm. Then, the hardness shows a slight fluctuation around a relatively stable value of 4.0 GPa. The hardness values obtained at the depths from 100 to 600 nm are used to plot a fitting curve by using the Nix-Gao model, with the H_o and h^* being calculated to be 2.7 GPa and 587.3 nm, respectively. Figure 4(b) shows that the measured hardness also has a constant decline trend, except for a little deviation at the depth of 200 nm. The fitting line obtained using the Nix-Gao model throughout the whole depth agrees well with the experimental results, especially for the hardness at the depth smaller than 150 nm. The calculated macroscopic hardness H_o and the characteristic scale-length h^* equal 3.7 GPa and 270.0 nm, respectively.

Figure 5 compares the hardness of W with different structures. It can be seen that the hardness for larger grain sized W (15 μm, full densification structure) is lower than that for smaller grain sized W (3 μm, with residue pores) when the penetration depth is less than 150 nm. However, the hardness for both types of W shows a comparatively synchronous downward trend at the depth from 150 to 400 nm, with the hardness for larger grain sized W being higher than that for smaller grain sized W. When the depth is larger than 400 nm, the hardness remains relatively stable values of 5 GPa and 4 GPa for large and small grain sized W, respectively.

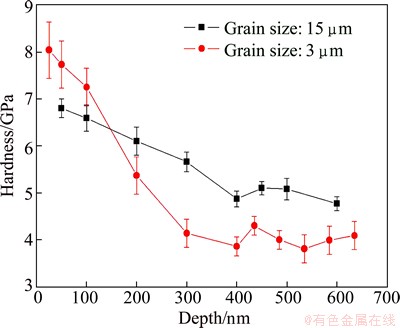
Fig. 5 Comparison of hardness between fully dense W and SPS-fabricated W

As mentioned by DURST et al [24], the characteristic scale-length h^* can be calculated using the scaling factor f for the definition of the storage volume for the GNDs:

             (3)

where b is the Burgers vector (0.286 nm for W), and α=0.5 is a constant, θ is the angle between the surface of the indenter and the plane of the indented surface, with tan θ=0.358 for Berkovich indenter, G=160 GPa is the shear modulus for W. Therefore, if the H_o and h^* are incorporated into Eq. (3), the scaling factor f for W with the grain sizes of 15, 3 and 4 μm can be calculated to be 1.30, 1.31 and 1.37, respectively.

It can be seen from Fig. 3 that the hardness has an abnormal increase at the depths around 400, 900 and 1300 nm. This phenomenon can be explained by the interaction between the PDZ boundary and grain/sub- grain boundary. The PDZ expands freely when the indenter penetrates through a single grain/sub-grain at the shallow contact between the indenter and the sample, and thus the hardness always shows a downward trend, which can be well fitted by the Nix-Gao model. Once the PDZ boundary approaches the grain/sub-grain boundary, the PDZ starts to interact with them. Therefore, the movement of dislocations containing in the PDZ is hindered by the boundary, leading to dislocation pile-up and multiplication. In reality, YANG and VEHOFF [28] revealed that hardness will increase with increasing h when the PDZ is confined within the indented grain/sub-grain, and they suggested that the relationship between the PDZ size and the indentation depth can be written as

                      (4)

where R is the indenter tip radius (R=100 nm in this work). For convenience, the horizontal axis in Fig. 3(b) is divided into three sections: section I (less than 400 nm), section II (from 400 to 2000 nm) and section III (larger than 2000 nm). Also, the depth at which the hardness starts to increase is defined as h₁ (400 nm), h₂ (900 nm) and h₃ (1300 nm) in Fig. 3(b) and the corresponding radii of the PDZ are defined as a_pz-h1, a_pz-h2 and a_pz-h3, respectively. Generally, as suggested by QIAO et al [33], the indenter tip radius could have an effect on the ISE. However, in this work the tip radius is relatively small and the effect of the indenter tip radius, R, is thus neglected. Then, the radius of the PDZ can be approximately written as

                               (5)

Putting h₁, h₂ and h₃ into Eq. (5), it can be obtained that a_pz-h1=2262 nm, a_pz-h2=5090 nm and a_pz-h3=7475 nm, respectively. Assuming that the initially contacted location between the indenter tip and the sample is at the center of the individual grain/sub-grain, the interaction between the PDZ boundary and the grain/sub-grain boundary leads to the increase of the hardness at the depth ~400 nm (h₁), ~900 nm (h₂) and ~1300 (h₃ ). It should be noted that the dimensions of the PDZ obtained at the depths of h₁, h₂ and h₃ were calculated to be 4000 nm (2a_pz-h1), 10000 nm (2a_pz-h2) and 15000 nm (2a_pz-h3), respectively. These three PDZ dimensions agree well with the grain/sub-grain size of W (from 3.5 to 15 μm), as shown in Fig. 2(b). The total hardness increment at the depth from 400 to 500 nm is 0.25 GPa, while the total hardness increments at the depths from 900 to 1100 nm and from 1300 to 1500 nm are 0.65 and 0.4 GPa, respectively. The discrepancy in the increment could be due to the interaction between the PDZ and sub-grain boundary being weaker than that between the PDZ and grain boundary. It should be noted that in section I the dimension of the PDZ is smaller than 2a_pz-h1 (4000 nm), similar to the lower limit of the sub-grain size (3.5 μm). That is, the PDZ will barely interact with grain/sub-grain boundary if the depth is less than 400 nm. This would be the evidence that the hardness always shows a downward trend at the depth lower than 400 nm. The hardness shows a relatively stable fluctuation around 5.0 GPa when the depth is larger than 1500 nm. These results are from the contribution of the interaction between the PDZ and grain boundary at the depth of h₃ (1300 nm). When the depth is larger than 1500 nm the dimension of the PDZ is calculated to be larger than 17500 nm, which is larger than that of all the individual grains. Consequently, the interaction between the PDZ and grain/sub-grain boundaries will definitely occur if the depth is larger than 1500 nm. It can thus be concluded that the increase of the hardness at specific depth is attributed to the interaction between the PDZ and grain or sub-grain boundaries, and after the dimension of the PDZ covers at least a complete grain, the corresponding indentation hardness starts to stabilize.

It can be seen from Fig. 4 that the hardness tends to reach a constant value when the depth increases to a specific value. The hardnesses of W with the grain sizes of 3 and 4 μm start to stabilize at depth of 400 nm and 550 nm, respectively. If the PDZs and the grain size are taken into consideration and the depths (400 and 550 nm) at which the hardness starts to stabilize are put into Eq. (5), it turns out that the dimensions of the PDZ are approximately 4500 and 6500 nm, respectively. These two dimensions are also larger than the individual grain sizes of the two types of W. From Fig. 5, it can be observed that hardness of different structured W starts to stabilize at the same depth of 400 nm, which means that the full densification structured W with the sub-grain size of 3.5 μm also reaches a constant indentation hardness if the dimension of the PDZ (4527 nm calculated using Eq. (4)) reaches the dimension of the individual sub-grain size. Therefore, it is further concluded that when the PDZ expands to an area covering a complete individual grain or sub-grain, the indentation hardness starts to stabilize.

The hardness for the SPS-fabricated W with a grain size of 3 μm and the full densification structured W with a sub-grain size of 3.5 μm (grain size of 15 μm) varies significantly, as shown in Fig. 5. This can be explained by the GBE or sub-GBE and the density difference between the two types of W. Firstly, with the depth less than 150 nm, the grain boundaries of the SPS-fabricated W (with a density of 82.5%) are high-angle boundaries, which cause a strong interaction between the PDZ and the grain boundaries. In contrast, the sub-grain boundaries in the full densification structured W are low-angle boundaries, which have a less inhibition to the expansion of the PDZ and this would result in a low indentation hardness. Secondly, after the depth being larger than 150 nm and with increasing the externally applied load, the porous structure of the SPS-fabricated W substantially decreases the indentation hardness. Thirdly, when the depth is larger than 400 nm, the local structure of the SPS-fabricated W underneath the indenter might be compressed densely and the indentation hardness would show a similarly stable trend as the full densification structured W, although the final hardness is smaller.

4 Conclusions

1) The corresponding macroscopic hardnesses for the three types of W are estimated to be 4.0, 2.7 and 3.7 GPa. The scaling factors are calculated to be 1.30, 1.31 and 1.37, respectively. It is revealed that the scaling factor is barely correlated with the grain/sub-grain size.

2) The interaction between the PDZ boundary and the grain/sub-grain boundary is believed to be the reason for the increase of the measured hardness at the specific depths. When the PDZ expands to an area covering a complete individual grain or sub-grain, the indentation hardness starts to stabilize.

References

[1] OLIVER W C, PHARR G M. An improved technique for determining hardness and elastic modulus using load and displacement sensing indentation experiments [J]. Journal of Materials Research, 1992, 7: 1564-1583.

[2] VLASSAK J J, NIX W D. Measuring the elastic properties of anisotropic materials by means of indentation experiments [J]. Journal of the Mechanics and Physics of Solids, 1994, 42: 1223-1245.

[3] SONG Min, SUN Ying-ying, HE Yue-hui, GUO Sheng-feng. Structure related hardness and elastic modulus of bulk metallic glass [J]. Journal of Applied Physics, 2012, 111: 053518.

[4] SONG Min, LIU Yong, HE Xiao-yu, BEI Hong-bin, HU Wei-ping, LIU Feng, LI Zhou. Nanoindentation creep of ultrafine-grained Al₂O₃ particle reinforced copper composites [J]. Materials Science and Engineering A, 2013, 560: 80-85.

[5] BULL S J. On the origins and mechanisms of the indentation size effect [J]. Zeitschrift für Metallkunde, 2003, 94: 787-792.

[6] SCHOLZ T,  J, SWAIN M V, SCHNEIDER G A. Indentation size effect in barium titanate with spherical tipped nanoindenters [J]. Applied Physics Letters, 2006, 88: 091908.

[7] MA Zeng-sheng, LONG Shi-guo, PAN Yong, ZHOU Yi-chun. Indentation depth dependence of the mechanical strength of Ni films [J]. Journal of Applied Physics, 2008, 103: 043512.

[8] FENG G, BUDIMAN A S, NIX W D, TAMURA N, PATEL J R. Indentation size effects in single crystal copper as revealed by synchrotron X-ray microdiffraction [J]. Journal of Applied Physics, 2008, 104: 043503.

[9] AMINI A, YAN W, SUN Q. Depth dependency of indentation hardness during solid-state phase transition of shape memory alloys [J]. Applied Physics Letters, 2011, 99: 021901.

[10] ARMSTRONG D E J, EDMONDSON P D, ROBERTS S G. Effects of sequential tungsten and helium ion implantation on nano- indentation hardness of tungsten [J]. Applied Physics Letters, 2013, 102: 251901.

[11] ELMUSTAFA A A, STONE D S. Indentation size effect in polycrystalline F.C.C. metals [J]. Acta Materialia, 2002, 50: 3641-3650.

[12] ABU Al-Rub R K, VOYIADJIS G Z. Analytical and experimental determination of the material intrinsic length scale of strain gradient plasticity theory from micro- and nano-indentation experiments [J]. International Journal of Plasticity, 2004, 20: 1139-1182.

[13] RESTER M, MOTZ C, PIPPAN R. Where are the geometrically necessary dislocations accommodating small imprints? [J]. Journal of Materials Research, 2009, 24: 647-651.

[14] ARSENLIS A, PARKS D M. Crystallographic aspects of geometrically-necessary and statistically-stored dislocation density [J]. Acta Materialia, 1999, 47: 1597-1611.

[15] RESTER M, MOTZ C, PIPPAN R. Microstructural investigation of the volume beneath nanoindentations in copper [J]. Acta Materialia, 2007, 55: 6427-6435.

[16] RESTER M, MOTZ C, PIPPAN R. Indentation across size scales—A survey of indentation-induced plastic zones in copper {111} single crystals [J]. Scripta Materialia, 2008, 59: 742-745.

[17] RESTER M, MOTZ C, PIPPAN R. The deformation-induced zone below large and shallow nanoindentations: A comparative study using EBSD and TEM [J]. Philosophical Magazine Letters, 2008, 88: 879-887.

[18] PETHICA J B, TABOR D. Contact of characterised metal surfaces at very low loads: Deformation and adhesion [J]. Surface Science, 1979, 89: 182-190.

[19] BULL S J, PAGE T F, YOFFE E H. An explanation of the indentation size effect in ceramics [J]. Philosophical Magazine Letters, 1989, 59: 281-288.

[20] BUSHBY A J, DUNSTAN D J. Plasticity size effects in nanoindentation [J]. Journal of Materials Research, 2004, 19: 137-142.

[21] NIX W D, GAO H. Indentation size effects in crystalline materials: A law for strain gradient plasticity [J]. Journal of the Mechanics and Physics of Solids, 1998, 46: 411-425.

[22] TAYLOR G I. Plastic strain in metals [J]. Journal of the Institute of Metals, 1938, 62: 307-324.

[23] CHICOT D. Hardness length-scale factor to model nano- and micro-indentation size effects [J]. Materials Science and Engineering A, 2009, 499: 454-461.

[24] DURST K, BACKES B, M. Indentation size effect in metallic materials: Correcting for the size of the plastic zone [J]. Scripta Materialia, 2005, 52: 1093-1097.

[25] FENG G, NIX W D. Indentation size effect in MgO [J]. Scripta Materialia, 2004, 51: 599-603.

[26] KIM J Y, LEE B W, READ D T, KWON D. Influence of tip bluntness on the size-dependent nanoindentation hardness [J]. Scripta Materialia, 2005, 52: 353-358.

[27] ABU Al-Rub R K. Prediction of micro and nanoindentation size effect from conical or pyramidal indentation [J]. Mechanics of Materials, 2007, 39: 787-802.

[28] YANG B, VEHOFF H. Dependence of nanohardness upon indentation size and grain size—A local examination of the interaction between dislocations and grain boundaries [J]. Acta Materialia, 2007, 55: 849-856.

[29] OKOLO B, WANNER A. Grinding-induced microstructural gradients and residual stresses in the surface layers of carbon steel and pure tungsten [J]. International Journal of Materials Research, 2006, 97: 1415-1424.

[30] BAHR D F, KRAMER D E, GERBERICH W W. Non-linear deformation mechanisms during nanoindentation [J]. Acta Materialia, 1998, 46: 3605-3617.

[31] LORENZ D, ZECKZER A, HILPERT U, GRAU P, JOHANSEN H, LEIPNER H S. Pop-in effect as homogeneous nucleation of dislocations during nanoindentation [J]. Physical Review B, 2003, 67: 172101.

[32] LIU Guang-yu, SONG Min, LIU Xin-li, NI Song, WANG Shi-liang, HE Yue-hui, LIU Yong. An investigation of the mechanical behaviors of micro-sized tungsten whiskers using nanoindentation [J]. Materials Science and Engineering A, 2014, 594: 278-286.

[33] QIAO X G, STARINK M J, GAO N. The influence of indenter tip rounding on the indentation size effect [J]. Acta Materialia, 2010, 58: 3690-3700.

压痕尺寸和晶粒/亚晶粒尺寸对高纯钨显微硬度的影响

刘光玉，倪 颂，宋 旼

中南大学 粉末冶金国家重点实验室，长沙 410083

摘  要：通过对不同结构的高纯钨进行微米和纳米压痕实验，发现压痕尺寸和晶粒/亚晶粒尺寸对材料的硬度有重要影响。探讨硬度的晶界效应和压痕尺寸效应。采用Nix-Gao模型，结合尺度因子对实验获得的压痕硬度值进行拟合。结果表明，尺度因子几乎与晶粒或亚晶粒的尺寸无关。塑性变形区与晶界或亚晶界之间的相互作用是导致硬度在某一特定深度增加的原因，而塑性变形区与晶粒或亚晶粒的尺寸几乎无关。当塑性变形区扩展增大到单个晶粒或亚晶粒尺寸时，压痕硬度开始趋于稳定。

关键词：高纯钨；压痕硬度；压痕尺寸效应；晶界；塑性变形区

(Edited by Xiang-qun LI)

Foundation item: Project (51174235) supported by the National Natural Science Foundation of China

Corresponding author: Min SONG; Tel: +86-731-88877677; E-mail: msong@csu.edu.cn

DOI: 10.1016/S1003-6326(15)63958-9