DOI: 10.11817/j.issn.1672-7207.2016.09.013
含碰撞的平面摩擦系统半解析半数值算法研究
王晓笋,巫世晶
(武汉大学 动力与机械学院,湖北 武汉,430072)
摘要:利用含平面库仑摩擦力系统的解析解结果,通过碰撞边界条件和时间的隐式关系,获得精确的碰撞时刻,由此确定从当前时刻到碰撞发生时的步长及平面上的碰撞位置。结合滑移/黏滞转换时位置和时刻的解析解,引入布尔变量B定义系统的状态,建立一种求解含碰撞的平面摩擦系统响应的数值算法。研究结果表明:该算法能够求解滑移/黏滞转换、碰撞以及平面滑移运动存在方向剧烈变化拐点时系统的响应,并有效地提高了系统响应的精度。
关键词:平面摩擦系统;碰撞;滑移/黏滞转换;精确解;数值算法
中图分类号:TH117.1 文献标志码:A 文章编号:1672-7207(2016)09-2997-08
Investigation of semi-analytical numerical algorithm for planar coulomb frictional system involving impacting
WANG Xiaosun, WU Shijing
(School of Power and Mechanical Engineering, Wuhan University, Wuhan 430072, China)
Abstract: The time and position for impacting were determined by studying the implicated relationship between the impacting boundary conditions and the time, and the time step for impacting was accurately solved. The Boolean variable B introduced was used to indicate the slipping, sticking and impacting state, and a new numerical algorithm was proposed by combining the close form solution for position and time of slip/stick transition. The results show that the new algorithm can provide responses involving slip/stick transition, impacting and the slip compromising sharp bending corners in planner slip problems with higher precision.
Key words: planner frictional system; impacting; slip/stick transition; close form solution; numerical algorithm
相互接触的2个部件发生相对运动诱发的摩擦行为对载荷传递和动态响应都会产生重要影响,如航空发动机叶片根部粗糙接触表面间的摩擦滑移消耗叶片系统振动能量而产生的干摩擦阻尼是降低叶片振动、延长发动使用寿命的关键因素[1]。摩擦力还能够引起局部刚度发生变化,诱发出现共振峰随激励量级增大而向低频移动的“频率漂移”典型非线性现象[2-3]。而非接触的2个部件由于相对运动在接触瞬间引发的碰撞能够使系统出现周期倍化序列、擦边分岔和混沌等一系列强非线性现象。虽然人们对于摩擦和碰撞进行了大量研究,但对于同时具有摩擦和碰撞的系统研究较少。通常在机械系统中,摩擦和碰撞往往是同时存在的,而且两者之间存在相互影响[4]。STRONGE[5]通过研究发现若摩擦因数过大,则在碰撞结束时直接进入黏滞状态。碰撞与摩擦都是强非线性因素,因此,含碰撞的摩擦系统具有大量非线性现象[6],如CONE等[7]采用数值法研究了带干摩擦的单自由度双面冲击振子, 结果表明系统存在周期倍化序列、擦边分岔(grazing bifurcation)以及黏滑碰撞运动。VIRGIN等[8]描述了包含库仑摩擦阻尼的双边谐激励碰撞振子的全局动力学,发现由于摩擦和碰撞诱发的擦边分岔与吸引盆等非线性现象。张有强等[9-12]研究了同时含有摩擦和碰撞系统的非线性动力学特性,发现较大的摩擦力使得系统逐渐趋于稳定单周期碰撞运动,而摩擦力较小时系统的运动多呈现为混沌行为。同时,摩擦力的幅值对全局分岔性态的影响比较复杂,尤其对混沌区和分岔点附近系统运动影响明显。目前,所有针对具有摩擦的碰撞系统的研究主要以研究其动态特性为主,而往往忽略了其准静态特性。具有库仑摩擦力的系统在外部载荷激励下可能处于滑移、黏滞和滑移/黏滞转换等不同状态,显然,含摩擦的碰撞系统在碰撞边界内部可能同时处于动态和准静态。为此,沈煜年等[13]使用事件驱动法求解碰撞响应,并通过入射角、法向相对速度、切向接触力与法向接触力的比值等判断碰撞、黏滞及滑移的开始和结束。钱震杰等[14]采用Hertz接触模型和Coulomb摩擦光滑修正模型分别建立法向和切向碰撞模型,根据接触对法向和切向距离建立碰撞/分离切换准则,并采用变步长计算,特别是对碰撞发生时的步长接近10-7时进行计算,由此提高系统的求解精度。显然,数值求解方法的精度依赖于步长,无法非常准确地确定碰撞的位置和时刻,从而影响整个系统响应的求解精度并导致累积误差不断增大。同时,采用数值法求解含有摩擦的碰撞问题时,还会出现黏滞/滑移转换导致的位置漂移和准静态状态下的数值振荡现象[15]。从目前对摩擦碰撞系统的研究发现,所建立的模型一般为一维模型,摩擦和碰撞仅限于1个方向,而工程实际中的摩擦碰撞往往是二维的,因此,采用传统数值方法来判断碰撞的发生和黏滞—滑移转换条件会更加困难,也会产生更大误差。最近,WANG[16]在路径坐标系下获得外载荷恒定时二维库仑摩擦力系统的精确解,准确地建立了黏滞/滑移转化的位置和时间。基于上述解析解,本文作者提出一种针对含摩擦的碰撞系统半解析半数值求解算法,不仅能够确定高精度的黏滞滑移转换位置与时间,而且能够确定准确的碰撞位置、速度与时间,可更加精确地分析摩擦碰撞系统动态和准静态特性。
1 含碰撞的平面摩擦系统动力学模型
含有碰撞的平面摩擦系统如图1所示。质量为m的质点在Oxy平面内通过弹簧及阻尼与边界连接,平面的外部激励载荷为Fe(t)=[Fx(t), Fy(t)]T,质点所受到的正压力为N(t),摩擦因数为m;u(t)=[x(t), y(t)]T表示质点在任意时刻的位置;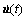 为质点在任意时刻t的运动速度;Fm(t)为平面库仑摩擦力,其定义为
为质点在任意时刻t的运动速度;Fm(t)为平面库仑摩擦力,其定义为
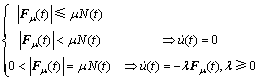 (1)
(1)
本文研究的平面碰撞问题将碰撞边界定义为2条垂直于x方向的直线,质点在Oxy平面运动时,在x方向上存在左边界xL和右边界xR。采用牛顿第二定律,可建立矩阵形式的系统运动方程为
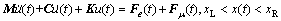 (2)
(2)
其中:M,C和K分别为质量矩阵,阻尼矩阵和刚度矩阵,M=diag[m, m], C=diag[cx, cy], K=diag[kx, ky]。质点的冲击碰撞方程为[11]
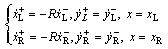 (3)
(3)
其中: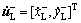 表示质点和左侧刚性边界x=xL发生碰撞之前的瞬时速度;
表示质点和左侧刚性边界x=xL发生碰撞之前的瞬时速度;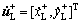 表示发生碰撞之后的瞬时速;
表示发生碰撞之后的瞬时速;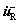 和
和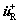 则分别表示质点和右侧刚性边界碰撞之前和之后的瞬时速度;R为速度恢复系数。R=1称为完全弹性碰撞,即没有能量损耗;0<R<1称为非完全弹性碰撞,系统由于碰撞存在能量损耗;R=0称为塑性碰撞,此时系统动能被完全损耗。本文考虑非完全弹性碰撞情况,即R<1。
则分别表示质点和右侧刚性边界碰撞之前和之后的瞬时速度;R为速度恢复系数。R=1称为完全弹性碰撞,即没有能量损耗;0<R<1称为非完全弹性碰撞,系统由于碰撞存在能量损耗;R=0称为塑性碰撞,此时系统动能被完全损耗。本文考虑非完全弹性碰撞情况,即R<1。
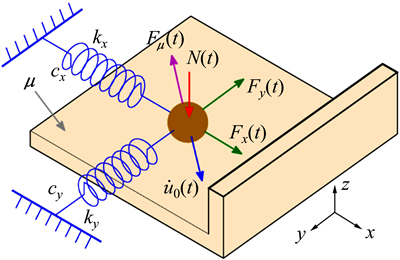
图1 含碰撞的平面摩擦系统模型
Fig. 1 Planner frictional system model involving impacting
2 黏滞滑移位置、时间的建立
滑移—黏附转化发生的时刻ts与对应的位置us(t)=[xs(t) , ys(t)]T可以表示为[16]
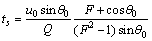 (4)
(4)
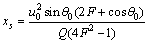 (5)
(5)
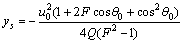 (6)
(6)
其中:u0为初始速度;Q为外部激励力、弹性力和阻尼力的合力,即
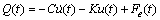 (7)
(7)
F=Fm(t)/Q(t),为量纲一的外部载荷,表示摩擦力与切向荷载的比率;q0为初始时刻u0与Q的夹角。
3 碰撞位置、速度与时间的确定
由文献[16]知该系统在恒定的外部激励力Q和摩擦力f作用下经过时间t后,作用时间t和角度θ存在着下列隐式关系:
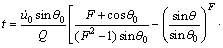
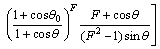 (8)
(8)
动态响应u(t)=[x(t),y(t)]T可以表示为[17]:
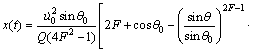
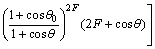 (9)
(9)
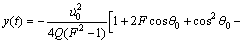
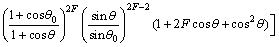 (10)
(10)
式(8)定义了作用时间t与角度θ的关系,若已知时间t,则能够确定当前时刻角度θ;反之,若已知当前时刻角度θ,则可以确定当前时刻t。虽然本文所研究的平面摩擦碰撞系统的外部激励力Q(t)是随时间变化的,但若积分步长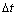 足够小,则在很短的时间内,Q(t)可认为近似恒定不变,因此,式(8)~(10)可以用于计算二维库仑摩擦力系统滑移过程中的动态响应。质点在平面Oxy的滑移过程中在下一个时间步内发生碰撞的条件为
足够小,则在很短的时间内,Q(t)可认为近似恒定不变,因此,式(8)~(10)可以用于计算二维库仑摩擦力系统滑移过程中的动态响应。质点在平面Oxy的滑移过程中在下一个时间步内发生碰撞的条件为
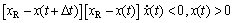 (11)
(11)
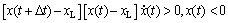 (12)
(12)
假设质点沿x正方向与右侧边界xR发生碰撞,则碰撞时必然存在
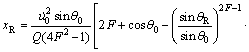
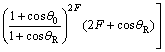 (13)
(13)
可确定xR与角度θR。对于此超越方程,可采用Newton-Raphson迭代法求解θR。求出θR后,将θ=θR代入式(8),可确定碰撞发生的时刻tR,从而确定从当前时刻到碰撞发生时系统的数值积分步长DtR=tR-t。再将θ=θR代入式(10),则可计算出系统在碰撞时质点y方向的位置。质点任意时刻的速度可以描述为[16]
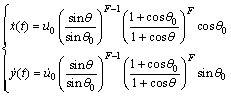 (14)
(14)
将θ=θR代入方程(13)则可以确定质点与右端边界条件碰撞瞬时的速度。根据冲击碰撞方程(3)确定发生碰撞之后的瞬时速度。
4 含碰撞平面摩擦系统的求解算法
含有摩擦力的系统在受到时变平面外部激励力激励时,系统可能处于滑移、黏滞和滑移/黏滞转换等多种状态。若再将碰撞边界引入,则系统的运动状态更加复杂。为此,首先引入1个布尔变量B用于描述二维库仑摩擦力系统的状态:B=1表示滑移状态,B=0表示黏滞状态。碰撞是一个瞬态过程,碰撞必然发生在滑移状态下,即碰撞时B=1。
对于滑移状态下的系统,可以采用定步长积分算法确定步长Dt,由此可以当前状态为初始条件,由式(8)确定t+Dt时刻的角度q,这样可直接由式(9)和(10)计算系统在下一时刻的位置。若B=1且F>1,则系统可能发生滑移/黏滞转换进入黏滞状态。黏滞时刻可以通过式(4)求得。若步长Dt>ts,则系统将会在t+ts时刻发生滑移/黏滞转换。利用式(5)和(6)计算黏滞位置,同时重新设置布尔变量B=0。若碰撞边界条件成立,则此时质点将与左/右边界发生碰撞。通过式(13)确定碰撞时的角度qR或qL,从而进一步确定碰撞发生的时刻(式(8))和y方向的位置(式(10))。而若B=0,则系统处于黏滞状态,但当F=1时,会发生黏滞/滑移转换,确定发生黏滞/滑移转换的时间,重新设置布尔变量B=1,系统进入滑移周期。系统的算法如图2所示。
本文算法中的计算结果是在由外部激励合力Q(t)定义的坐标系(y轴与外部激励力Q(t)的方向正好相反)下获取的,因此,该坐标系随着时间是动态变化。利用上述算法求解获得的响应还需要进行坐标转换,从而最终得到系统的动态响应。
5 算例分析
系统的参数设置如下,质量m=1,刚度系数kx=ky=10,cx=cy=0.1,碰撞边界条件设置为xL=-0.02,xR=0.02。外部激励为
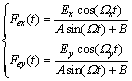 (15)
(15)
外部激励表达式内的参数设置为Ex=Ey=1.0, Wx=Wy=1.0,A=0.5,B=0.4,W=10.0,速度恢复系数R=0.95,mN(t)=1.0。积分步长设置为Dt=10-4。
采用本文所提出的求解算法获得的系统响应如图3~14所示。其中,图3~8所示分别为系统的x和y方向的位移和速度的时间历程曲线。从图3~8可以发现:摩擦力作用下的碰撞过程中能量消耗较大,系统在经历了短暂的瞬态响应之后随即进入稳态响应。从图4和图6的x方向位移及速度的局部放大图可以发现:每个完整的碰撞周期均最终以发生黏滞结束;系统在发生最后1次碰撞之后随即发生滑移—黏滞转换[5],但黏滞位置与碰撞位置之间并未重叠;若速度恢复系数R更小或者摩擦因数m更大,则碰撞过程会更快转换进入黏滞状态。从图7和图8可见:y方向每个周期内出现4次滑移—黏滞转换,而当x方向发生碰撞时,y方向的响应则保持滑移状态不变。
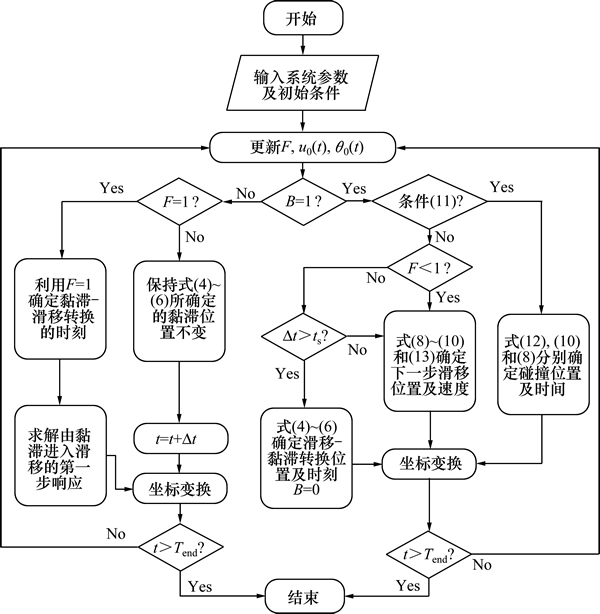
图2 算法程序流程图
Fig. 2 Flowchart of algorithm
图9所示为系统进入稳态响应之后碰撞过程中相邻碰撞点内碰撞周期Ti的变化规律。从图9可见:在库仑摩擦力作用下,在1~32次碰撞之间(图9所示的含有正方形的实线),碰撞周期逐渐减小,频率逐渐增高;在碰撞过程末段,从第33次碰撞开始(图9所示含有圆圈的实线),碰撞周期又逐渐增加,直至最终进入黏滞状态。
质点与碰撞边界发生连续碰撞,是因为外部激励力作用下始终迫使质点朝碰撞边界方向运动。碰撞之后瞬时速度矢量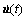 的角度
的角度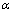 和激励力合力Q(t)的角度β如图10所示。从图10可见:碰撞发生之前
和激励力合力Q(t)的角度β如图10所示。从图10可见:碰撞发生之前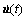 和Q(t)几乎同向,接近于碰撞平面的法线方向,角度差别很小,第1次碰撞之后
和Q(t)几乎同向,接近于碰撞平面的法线方向,角度差别很小,第1次碰撞之后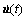 和Q(t)之间的角度接近p;随着碰撞进行,角度
和Q(t)之间的角度接近p;随着碰撞进行,角度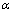 不断减小,而角度b则不断增加,最终角度
不断减小,而角度b则不断增加,最终角度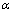 趋近于p/2,即质点近似进行垂直方向运动,而此时角度b也接近p/2,
趋近于p/2,即质点近似进行垂直方向运动,而此时角度b也接近p/2,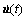 和Q(t)在碰撞过程的末端再次接近同向,且都接近于碰撞平面的切线方向,因此,也导致图9所示碰撞间距在起始阶段较大,但每次碰撞之后初始角度
和Q(t)在碰撞过程的末端再次接近同向,且都接近于碰撞平面的切线方向,因此,也导致图9所示碰撞间距在起始阶段较大,但每次碰撞之后初始角度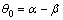 会逐渐减小,因此,碰撞间距也随着q0的减小而变小。在碰撞末段,
会逐渐减小,因此,碰撞间距也随着q0的减小而变小。在碰撞末段,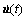 和Q(t)又接近同向,但碰撞和摩擦消耗了大量动能导致此时起始速度
和Q(t)又接近同向,但碰撞和摩擦消耗了大量动能导致此时起始速度 很小,因此,碰撞时间间距在末段有轻微升幅。
很小,因此,碰撞时间间距在末段有轻微升幅。
图11所示为本文计算的碰撞位置与理论碰撞位置之差的绝对值。从图11可见:采用式(13)能够精确地计算出碰撞位置及碰撞时间,而碰撞位置的精度接近10-10。若采用传统的数值积分算法,则无法准确地捕获碰撞位置,导致碰撞数值积分获取的碰撞位置在理论位置附近出现振荡。本文算法所获得的碰撞位置精度远高于传统的数值积分算法所获精度,体现了本文算法在求解碰撞问题响应精度方面的优越性。
图12所示为从起始状态开始直至最终进入稳态的不同时间区间内的运动轨迹。从图12可以发现:碰撞周期内系统的轨迹在每次碰撞发生之后会产生强烈变化,因此多次出现拐点,而这会导致传统的数值积分算法出现积分误差,多次拐点的出现则使得传统积分算法获得的结果出现更大的累积误差。本文所建立的求解算法能够避免拐点处的数值积分误差,从而提高系统动态响应的求解精度。而当系统进入稳态响应之后,随着时间的变化,系统的轨迹曲线包括碰撞点和黏滞位置均反对称于x轴和y轴,这是含碰撞的平面摩擦系统所具有的运动特性。
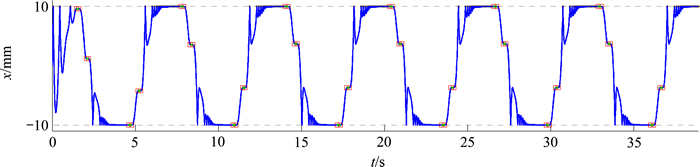
图3 x方向的位移时间历程曲线
Fig. 3 Time history of displacement in x direction
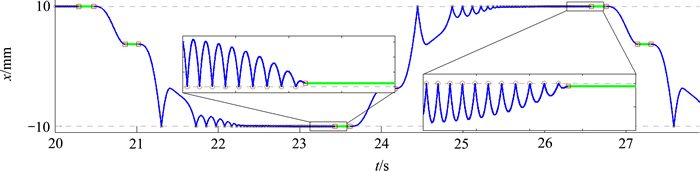
图4 x方向的位移时间历程曲线局部放大图
Fig. 4 Enlarged plot of time history of displacement in x direction
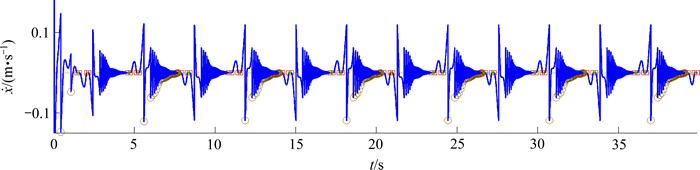
图5 x方向的速度时间历程曲线
Fig. 5 Time history of velocity in x direction
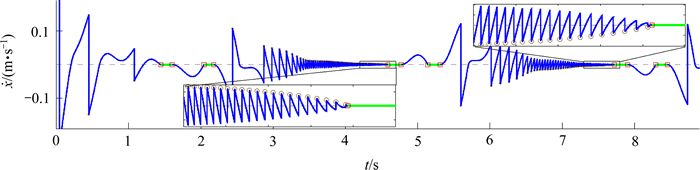
图6 x方向的速度时间历程曲线的局部放大图
Fig. 6 Enlarged plot of time history of velocity in x direction
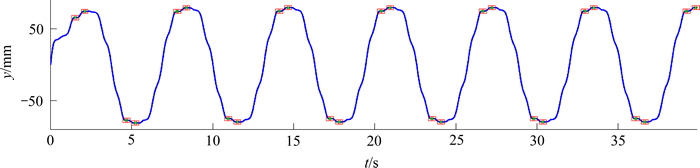
图7 y方向的位移时间历程曲线
Fig. 7 Time history of displacement in y direction
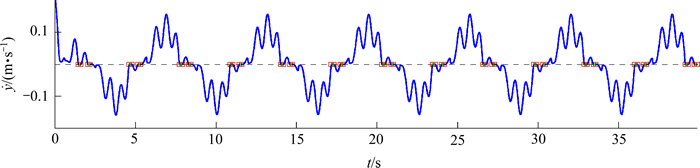
图8 y方向的速度时间历程曲线
Fig. 8 Time history of velocity in y direction
此外,在没有碰撞边界的条件下,式(14)所确定的外部激励力会始终位于单位摩擦圆(已知mN(t)=1.0)的外部[17],因此,系统会保持持续的滑移运动状态。但引入碰撞边界条件之后,在碰撞边界所发生的多次碰撞与摩擦力一起诱发了极大的能量损耗,最终使得平面摩擦系统在碰撞结束之后发生滑移—黏滞转换。
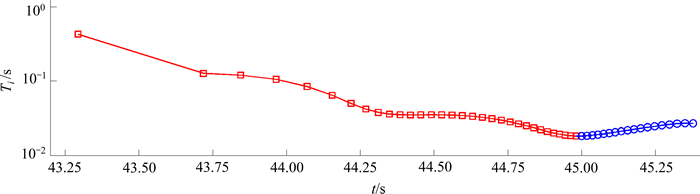
图9 碰撞周期变化规律
Fig. 9 Evolution law of duration between two adjacent impacts
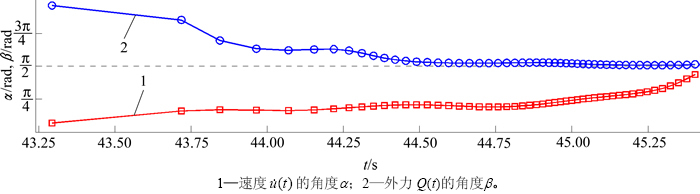
图10 碰撞起始阶段速度 的角度a与外力Q(t)的角度β随时间的变化规律with time
的角度a与外力Q(t)的角度β随时间的变化规律with time
Fig. 10 Variation laws of angle of a and β with time
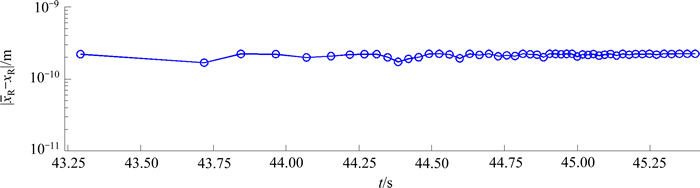
图11 碰撞瞬时计算碰撞位置与理论位置之差
Fig.11 Error between theoretical impacting position and calculated position
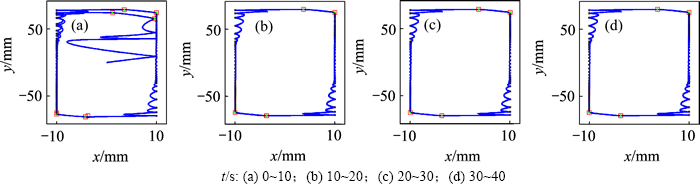
图12 系统轨迹
Fig. 12 Orbits of system
6 结论
1) 含碰撞的二维平面摩擦系统在碰撞周期末段均会发生滑移—黏滞转换并最终进入黏滞状态,但黏滞的位置与碰撞边界并不会完全重合,而是存在微小的偏差。碰撞的存在也诱发了相邻滑移段内的滑移—黏滞转换。在碰撞开始阶段,系统的轨迹多次出现剧烈的方向变化。
2) 建立了含碰撞的平面摩擦系统的滑移—黏滞转换和碰撞的位置和时间的表达式,提出了一种半解析半数值的新算法。该算法在求解系统响应的过程中能够精确地获取系统黏滞—滑移转换及碰撞的位置和时刻,能够克服传统数值积分算法求解该类问题时存在的数值振荡、跳跃等现象,并有效降低累积积分误差,提高求解精度。
参考文献:
[1] WETTERGREN H L. Optimal design to reduce dynamic instability of a turbine generator due to microslip[J]. Journal of Sound and Vibration, 1998, 214(1): 57-66.
[2] OWEN D R. Structured deformations and the refinements of balance laws induced by microslip[J]. International Journal of Plasticity, 1998, 14(1): 289-299.
[3] GAUL L. Nonlinear dynamics of structures assembled by bolted joints[J]. Acta Mechanica, 1997, 125(1): 169-181.
[4] BEGLEY C J. Impact response and the influence of friction[J]. Journal of Sound and Vibration, 1998, 211(5): 801-818.
[5] STRONGE W J. Smooth dynamics of oblique impact with friction[J]. International Journal of Impact Engineering, 2013, 51(1): 36-49.
[6] HINRICHS N. Dynamics of oscillators with impact and friction[J]. Chaos, Solutions & Fractals, 1997, 8(4): 535-558.
[7] CONE K M, ZADOKS R I. A numerical study of an impact oscillator with addition of dry friction[J]. Journal of Sound and Vibration, 1995, 188(5): 659-683.
[8] VIRGIN L N, BEGLEY C J. Grazing bifurcations and basins of attraction in an impact-friction oscillator[J]. Physica D, 1999, 130(1): 43-57.
[9] 张有强, 丁旺才. 干摩擦对碰撞振动系统周期运动的影响分析[J]. 振动与冲击, 2009, 28(6): 110-112, 134.
ZHANG Youqiang, DING Wangcai. Study on effect of dry friction on periodic motion of impact vibration system[J]. Journal of Vibration and Shock, 2009, 28(6): 110-112, 134.
[10] 张有强, 丁旺才, 孙闯. 单自由度含间隙和干摩擦碰撞振动系统的分岔与混沌[J]. 振动与冲击, 2008, 27(7): 102-105, 130.
ZHANG Youqiang, DING Wangcai, SUN Chuang. Bifurcation and chaos of one degree of freedom impact vibration system with clearance and dry friction[J]. Journal of Vibration and Shock, 2008, 27(7): 102-105, 130.
[11] 周鹏, 李贵杰. 干摩擦下含双侧间隙碰撞振动系统的动力学分析[J]. 机械工程与自动化, 2014, 182(1): 4-6.
ZHOU Peng, LI Guijie. Dynamics analysis of vibro-impact system with coupling clearance and dry friction[J]. Mechanical Engineering & Automation, 2014, 182(1): 4-6.
[12] 刘占生, 张敏, 张广辉, 等. 基于LuGre摩擦模型的叶片碰撞摩擦特性研究[J]. 振动与冲击, 2012, 31(12): 172-178.
LIU Zhansheng, ZHANG Min, ZHANG Guanghui, et al. Characteristics of impact-contact and friction between tips of blades based on LuGre model[J]. Journal of Vibration and Shock, 2012, 31(12): 172-178.
[13] 沈煜年, 顾金红. 柔性梁含摩擦斜碰撞的刚体-弹簧-质点混合模型研究[J]. 振动工程学报, 2016, 29(1): 1-7.
SHEN Yunian, GU Jinhong. Research on rigid body-spring- particle hybrid model for flexible beam under oblique impact with friction[J]. Journal of Vibration Engineering, 2016, 29(1): 1-7.
[14] 钱震杰, 章定国. 含摩擦碰撞柔性机械臂动力学研究[J]. 振动工程学报, 2015, 28(6): 879-886.
QIAN Zhenjie, ZHANG Dingguo. Frictional impact dynamics of flexible manipulator arms[J]. Journal of Vibration Engineering, 2015, 28(6): 879-886.
[15] BARBER J R, WANG X S. Numerical algorithms for two-dimensional dynamic frictional problems[J]. Tribology International, 2014, 80: 141-146.
[16] WANG X S. Trajectory of a projectile on a frictional inclined plane[J]. American Journal of Physics, 2014, 82(8): 764-768.
[17] WANG X S, BARBER J R. Numerical frictional algorithm with implementation of closed form analytical solutions[J]. Computer Methods in Applied Mechanics and Engineering, 2016, 300(3): 643-656.
(编辑 陈灿华)
收稿日期:2016-03-01;修回日期:2016-05-02
基金项目(Foundation item):国家重点基础研究发展计划(“973”计划)项目(2014CB239203);国家自然科学基金资助项目(51575403,51375350,51005170) (Project(2014CB239203) supported by the National Basic Research Development Program (973 Program) of China; Projects(51575403, 51375350, 51005170) supported by the National Natural Science Foundation of China
通信作者:王晓笋,副教授,硕士生导师,从事机电传动与智能控制技术、机械摩擦与磨损研究;E-mail: wxs@whu.edu.cn