DOI: 10.11817/j.ysxb.1004.0609.2021-37740

水平层状优势节理石灰岩采空区顶板破坏特征及其影响机制

姜立春^{1, 2}，张  浩¹，王建德³

(1. 华南理工大学 安全科学与工程研究所，广州 510640；

2. 华南理工大学 土木与交通学院，广州 510640；

3. 广东省安全生产科学技术研究院，广州 510640)

摘  要：为研究层状石灰岩采空区顶板的破坏特征及影响机制问题，在梅州某地下矿调研的基础上，构建采空区水平层状优势节理顶板力学模型，推导其应力分量表达式；结合M-C岩体强度准则，给出任意点岩体破坏判定值Z及其峰值数学式，分析顶板可能出现的变形破坏类型及失稳特征。结果表明：顶板的顶部、下部、两侧翼等位置出现4个判定峰值区域，依照Z值大小排序，分别对应脱落型(Ⅰ类)、挠曲型(Ⅱ类)、剪切型(Ⅲ类)等3种可能变形破坏形式。当Ⅰ、Ⅱ类变形破坏时，顶板具有“梯形拱”承载效应；当Ⅲ类变形破坏时，顶板具有类似“工”型承载特征。顶板破坏类型受安全系数m、跨厚比n和侧压系数k₀等因素影响，其中，m、n为可控因素，k₀为不可控因素。当k₀和n既定时，m仅影响Ⅰ、Ⅱ类或Ⅰ、Ⅲ类破坏类型之间的转化，临界处m分别为2.02和1.22；当m和n既定时，k₀影响方式与m的方式相同，临界处k₀分别为1.25和1.33；当m和k₀既定时，n将影响Ⅰ、Ⅱ、Ⅲ类等3种破坏类型之间转化，临界处n为1.6和3.5。采空区现场勘察结果验证理论分析结果的合理性。成果为此类矿山采空区顶板参数选择提供理论依据。

关键词：石灰岩采空区；变形破坏类型；影响机制；顶板安全系数；跨厚比

文章编号：1004-0609(2021)-01-0222-12　　     中图分类号：TU457　　     文献标志码：A

引文格式：姜立春, 张  浩, 王建德. 水平层状优势节理石灰岩采空区顶板破坏特征及影响机制[J]. 中国有色金属学报, 2021, 31(1): 222-233. DOI: 10.11817/j.ysxb.1004.0609.2021-37740

JIANG Li-chun, ZHANG Hao, WANG Jian-de. Analysis of roof failure characteristics and influence mechanism in limestone goaf with horizontal layered dominant joints[J]. The Chinese Journal of Nonferrous Metals, 2021, 31(1): 222-233. DOI: 10.11817/j.ysxb.1004.0609.2021-37740

石灰石是建筑行业的基础原料，具有价格低、赋存量大、分布广等特点，目前国内外普遍采用露天开采方式进行开采^[1]。受环境政策的制约，规模化地下开采石灰石矿，梅州是全国仅有的特例，强力支撑当地水泥行业的发展。经过数年开采，该地区遗留了大量采空区，安全性问题突出^[2-3]。地质调查表明，梅州石灰石矿床普遍为层状节理产出，倾角为水平或缓倾斜，在空间上呈现明显各向异性特征。研究采空区顶板破坏类型及影响机制，有利于矿山安全生产。

目前，国内外采空区顶板领域相关研究涉及金属矿、煤矿等矿床^[4-16]，研究方法主要包括：相似材料实验^[4-6]、数值模拟^[7-9]、理论分析^[10-17]等。在采空区的相似实验研究方面，吴爱祥等^[4-5]通过相似材料实验、位移监测等手段，对采空区的冒落过程、特征以及机理进行深入研究，并提出了相应的控制措施；FU等^[6]结合相似试验和数值模拟方法研究了采空区群形成过程中应力应变演化规律。在数值模拟方面，学者主要采用有限元(ANSYS、MIDAS)、有限差分(FLAC3D)等方法对采空区顶板稳定性进行分析^[7]，如MURPHY等^[8]利用数值模拟方法研究了软弱带位置对石灰石采空区稳定性的影响，发现软弱带位于底板时采空区的稳定性最差；张敏思等^[9]利用RFPA软件模拟了采空区顶板在开挖过程的损伤变化规律，计算了顶板的临界安全厚度。采空区顶板破坏机理方面，有学者提出了压力拱假说^[11-12]、块体理论^[13]、砌体梁理论^[14]等。如姜立春等^[11]基于拱架效应研究了采空区尺寸及充填接顶率对采空区稳定性的影响；BRADY等^[12]发现赋存层状岩体的矿床顶板也具有拱承载效应，提出了层状顶板的三类破坏方式并给出其安全系数计算式；陈虎等^[13]基于梁理论和块体理论，研究了顶板厚度对层状顶板的三类破坏形式变化规律的影响；钱鸣高等^[14]提出了采场上覆围岩“砌体梁”结构力学模型并进行深入研究，使其在煤炭开采领域应用良好。近年来，突变理论被应用到采空区顶板失稳研究中，取得了一定的研究成果^[15-17]。综上所述，相关研究研究鲜有涉及地下石灰石矿采空区领域，尚未关注层状优势节理对此类采空区顶板的稳定影响问题。

本文以梅州某石灰石矿采空区顶板为对象，在现场调查的基础上，将层状优势节理石灰岩视为横观各向同性体，建立水平层状优势节理采空区顶板的力学模型，利用其相容方程，给出顶板任意一点的应力分量表达式。结合Mohr-Coulomb岩体强度准则，分析采空区顶板的破坏类型及特征，研究影响因素对其破坏机制，结合工程实例，验证理论分析结果的科学性，指导矿山安全生产。

1  水平层状节理顶板力学模型及理论求解

1.1  力学模型

梅州地下石灰石矿山采用房柱空场法开采。由于石灰石层状节理在垂直方向上线密度较为接近，水平方向各向异性较弱，因此可将其理想化为横观各向同性体，研究其本构关系^[18]。在现场调研的基础上，以单元采空区为例，构建水平层状优势节理石灰岩顶板力学模型(见图1)。其中，图1(a)所示为单元采空区结构图，图1(b)所示为顶板受力模型图。顶板上部受到上覆岩层重力q作用。

假设顶板两端简支，两侧受支持力F_t以及侧压力F_n。在图1(b)中，顶板厚度h，跨度为2l。坐标系原点位于顶板中心，水平方向为x轴方向，沿顶板垂直向下为y轴正方向。

1.2  应力求解

图1  顶板力学模型

Fig. 1  Mechanical model of roof

对于图1(b)所示的平面应变问题，在不考虑体力的情况下，横观各向同性岩体的相容方程可以表示为^[19]

                    (1)

式中：Ф为应力函数，即Airy应力函数^[19]；E₁、E₂分别为各向同性面(水平面)上与垂直各向同性面(y轴方向)的弹性模量；μ₁、μ₂为水平面上与y轴方向的泊松比；G₂为y轴方向的剪切模量。

为简化代数式，令，。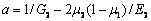

根据弹性力学半逆解法原理^[20]，假设顶板上部的垂直应力均匀分布，即。则水平应力()、垂直应力()、剪切应力()可分别表示为

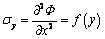，，     (2)

将式(2)积分可得

                      (3)

式中：、、是关于y的待定函数。将式(3)带入式(1)，可得

  (4)

式(4)为x的一元二次方程，因此需满足x的各项系数以及常数项为0，从而可求解得到、、表达式，进而推导出应力函数Ф的表达式：

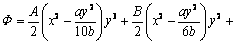
  (5)

式中：A、B、C、D、E、F、G、H、K为待定常数；γ为上覆岩体平均容重；h₀为顶板埋深。

由边界条件及侧压力计算方法^[3]，可以求得积分常数A~K的值，其中，，，，，，，。

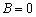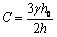侧压系数用k₀表示，即

                                  (6)

式中：F_n为侧压力

整理式(2)和式(4)，并代入积分常数，可求得应力分量、、表达式：

   (7)

式中：压应力方向为正。

2  破坏类型、特征及过程分析

梅州石灰石矿岩呈水平层状产出，岩体结构整体好，采空区顶板有别于其他节理发育破碎的矿体顶板，其破坏形式具有鲜明的特色。因此，本节基于顶板安全系数法，尝试通过计算岩体破坏判定值Z，分析顶板的Z峰值空间分布，研究该类采空区顶板破坏类型、特征及过程。

2.1  顶板岩体破坏判定值Z及峰值求解

1) 顶板岩体破坏判定值Z

Mohr-Coulomb强度准则能较好地反映顶板岩体的破坏方式^[20-21]。这里引入顶板安全系数m作为约束条件，设定顶板岩体破坏判定值为Z，根据M-C强度破坏准则，可得Z的数学表达式为

                        (8)

式中：m为顶板安全系数；为剪应力；c₀为黏聚力；为正应力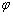；为内摩擦角。

当Z＜0，表示该处岩体未发生破坏；当Z=0，表示该处岩体处于临界破坏状态；当Z＞0，表示该处岩体破坏。

将式(7)中的水平应力()、垂直应力()、剪切应力()代入式(8)，结合莫尔-库伦应力圆的属性^[22]，可得顶板岩体破坏判定值Z的综合表达式：

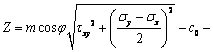
   (9)

综合式(7)和式(9)分析可知，顶板岩体破坏定值Z与弹性模量、泊松比、黏聚力、顶板安全系数、顶板尺寸等参数密切相关。Z越大，则该处岩体越容易破坏。对于某确定的研究对象，式(9)中弹性模量、泊松比、黏聚力等物理力学参数为定值，因此，通过研究顶板的其他参数即可求解顶板任意位置的判定值Z大小。

为了便于后续分析，这里引入跨厚比n来表示采空区跨度与厚度之间的关系，即n=2l/h。

2) 判定值Z峰值

利用MATLAB工具包对式(9)进行极值求解，发现顶板区域判定值Z有4个峰值，分别位于顶板上部、两侧翼和下部的中间。在图1(b)坐标系中分别为(0, -h/2)、(l, 0)、(-l, 0)、(0, h/2)。由模型对称性可知(见图1)，顶板左右两侧判定值应大小相等，即可用Z_a、Z_b、Z_c分别表示上部、侧翼和下部的峰值。结合式(7)与峰值点坐标，整理可得顶板区域判定值Z峰值表达式为

  (10)

式中：a、b为含弹性模量和泊松比的简化式，其中，，。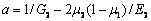

由式(10)可知，对于某特定的研究对象，岩体失稳判定Z峰值大小的影响因素分别为侧压系数k₀、顶板安全系数m及顶板跨厚比n。

2.2  破坏类型、特征

由2.1节分析知，顶板区域岩体破坏判定值Z的4个峰值分别位于顶板上部、下部以及两侧中心位置(见图2)。由于顶板受力具有对称性分布特征，左右两侧Z值相等。因此，4个峰值可分别用Z_a、Z_b、Z_c进行表示。

1) 脱落型变形破坏(Ⅰ类)

由受力分析可知，顶板下部比上部更容易破坏，上部判定值Z_a通常要小于上部判定值Z_c。Z_a、Z_b、Z_c的大小排序存在以下3种情况：Z_a＜Z_c＜Z_c、Z_b＜Z_a＜Z_c、Z_a＜Z_c＜Z_b，对应的可能变形破坏类型分别设定为Ⅰ类、Ⅱ类、Ⅲ类等。

图2  判定值Z峰值分布位置示意图

Fig. 2  Diagram for location of peak value of Z

当Z_a＜Z_b＜Z_c时，顶板先从采空区顶板下部区域开始破坏，再延伸至顶板两侧区域，最后引起顶板上部区域破坏。在实际工程中，采空区顶板由于中间及侧边脱落而破坏，在上部区域破坏前可能已经大面积垮塌。即脱落型破坏。

2) 挠曲型变形破坏(Ⅱ类)

当Z_b＜Z_a＜Z_c时，顶板先从采空区顶板下部区域开始破坏，再延伸至顶板上部区域，最后引起顶板两侧区域破坏。在实际工程中，采空区顶板发生挠曲破坏，在两侧区域发生破坏前已经贯通垮塌，即挠曲型破坏。挠曲型破坏的顶板厚度通常较小。

3) 剪切型变形破坏(Ⅲ类)

当Z_a＜Z_c＜Z_b时，顶板先从采空区顶板两侧区域开始破坏，再延伸至顶板下部区域，最后引起顶板上部区域破坏。在实际工程中，由于采空区顶板从两侧区域先发生破坏，属于典型剪切型破坏。顶板通常在没有预兆的情况下引起大面积垮塌，危险性大。但由于其顶板厚度较大，安全系数储备值也往往过高，发生概率相对较低。

当单元采场回采结束后，采空区上覆岩体将形成应力拱，承载上部围岩的重力荷载^[11]。Ⅰ、Ⅱ类破坏从顶板下部区域开始，在其他部位发生破坏前属于正常冒落，顶板由于拱架效应保持稳定。Ⅲ类破坏没有明显的拱架效应顶板往往发生突发失稳破坏。

2.3  破坏过程

由现场调查及文献[13]知，层状节理岩体巷道顶板垮塌后的形状可视为等腰梯形。当采空区顶板可能发生Ⅰ、Ⅱ类破坏时，考虑内部结构具有对称性的特点，其承载结构可简化为图3所示的梯形拱。

图3  “梯形拱”承载结构示意图

Fig. 3  Diagram for bearing structure of “trapezoid arch”

1) 在Ⅰ类破坏过程中，顶板侧翼区域发生破坏，表明图3中两侧承载结构的承载厚度变小，应力增大。当应力超过承载极限时，两侧承载结构将破坏，承载结构失效。因此，可将顶板侧翼进入破坏视为顶板进入亚稳定状态。

2) 在Ⅱ类破坏过程中，顶板上部区域发生破坏，表明图3中上部承载结构的承载厚度变小，应力增大。当应力超过承载极限时，上部承载结构将破坏，承载结构失效。因此，可将顶板上部进入破坏视为顶板进入亚稳定状态。

3) 在Ⅲ类破坏过程中，顶板承载区域类似“工”型结构，此时，顶板将不呈现出“梯形拱”特征。由“工”型梁的承载方式可知^[22]，采空区结构失效主要由“工”型的翼缘或腹板破坏诱发所致。

为了发挥岩土体自有的拱架效应，在实际工程中，采区顶板应该预留合理的厚度，控制空间形态，在保证安全的前提下提高回采率。对于梅州石灰石矿山而言，应综合考虑回采率和安全性，合理控制变形破坏类型。

2.4  算例分析

1) 工程概况

根据矿山地质资料，梅州某地下石灰石矿体为栖霞组灰岩，呈水平厚层状产出，优势节理走向连续，节理间距小，节理间无充填物，岩体内部结构致密，整体性好，岩石质量指标(RQD)为81.20%。

矿山设计开采+115 m、+95 m、+60 m、+35 m、+7 m、-21 m、-48 m、-75 m等8个水平中段，矿柱宽度为15.0 m。为了确保安全，矿山采取预留厚大顶板和保安矿柱支撑采空区，顶板普遍厚度在12.0 m以上，资源回采率不足30%。目前+7 m水平以上5个中段矿体回采结束，现正开采-21 m水平中段。

下面以+35 m水平中段采空区为例，利用式(9)和式(10)对顶板可能的破坏类型进行分析，计算采空区顶板的最小安全理论厚度，并与之前预留的顶板厚度进行比较，判断其合理性。

2) 参数选取

根据矿山地质资料，石灰石矿体的物理力学参数如表1所列，其中，σ_c、σ_t分别为单轴抗压强度、抗拉强度，其余物理力学参数取值见第1.2节和第2.1节。+35 m水平中段平均赋存深度约为107.0 m，设计矿房跨度15.0 m。这里顶板安全系数取值范围为1.0~3.0，顶板厚度小于或等于跨度，侧压系数k₀取1.0。

3) 数值计算

为研究顶板判定值Z空间分布，先通过求解顶板应力分布，再利用式(9)分析采空区顶板不同跨厚比n和顶板安全系数m组合工况情况。在数值计算过程中，扩大跨厚比n和顶板安全系数m的取值范围，确保计算结果涵盖三种破坏类型，更贴近实际工程。其中，跨厚比n取1.0~3.5，顶板安全系数m取值范围为1.0~4.0。

4) 破坏特征分析

限于篇幅限制，这里直接给出符合Ⅰ类、Ⅱ类、Ⅲ类等3种破坏类型的工况计算结果(见图4)。其中，图4(a)对应Ⅰ类破坏类型，此工况条件下跨厚比n=2.1，顶板安全系数m=1.5；图4(b)对应Ⅱ类破坏类型，此工况条件下跨厚比n=3.0，顶板安全系数m=2.1；图4(c)对应Ⅲ类破坏类型，此工况条件下跨厚比n=1.5，顶板安全系数m=1.5。

由图4(a)、(b)可以发现，在Ⅰ、Ⅱ类破坏类型中，顶板先由下部中心区域开始冒落，形成“梯形拱”。此后破坏有垂直拱轴往下发展的趋势，表明拱架有效承载面积不断缩减小，应力值逐渐增大；当应力增加至一定范围时，“梯形拱”将无法维持自稳发生垮塌。此时，在图4(a)中，白色虚线框以下部分为顶板可能的冒落区域；在图4(b)中，顶板下端、上端、侧边均已发生破坏，顶板极有可能已经发生失稳垮塌。

表1  石灰岩体物理力学参数

Table 1  Mechanical parameters of limestone

图4  顶板3种破坏类型等值线彩云图

Fig 4  Color contour maps for 3 failure types of roof

由图4(c)可以发现，Ⅲ类破坏类型中，顶板中心承载区域类似“工”型，不呈现“梯形拱”特征，侧翼和下部区域的破坏将导致“工”型的腹板和翼缘承载厚度减小，应力值逐渐增大；当顶板翼缘的破坏程度过大，顶板将无法维持稳定。此时，图4(c)中判定值Z均小于0，理论上顶板没有任何部位发生破坏。

5) 最小安全厚度

合理选择顶板厚度可以充分发挥采空区顶板的“梯形拱”效应^[10-11]，同时避免Ⅲ类破坏的发生，有利于提高资源回采率。此时，必须满足Z_a＜0，Z_b＜0。

在顶板跨度既定、无外部动力荷载条件下，顶板取安全系数m=1.8^[10]，则由式(9)计算可得采空区顶板理论最小安全厚度为7.2 m。绘制顶板Z等值线分布彩云图如图5所示。图5中红色虚线框内为可能出现的“梯形”冒落区域。

图5  Z等值线彩云图(n=2.08，m=1.8)

Fig. 5  Color contour map for Z (n=2.08, m=1.8)

6) 对比分析

为了对比分析，取顶板安全系数m=1.8，跨厚比n=1.25，即顶板厚度为12.0 m；同理计算并绘制其顶板判定值Z等值线分布彩云图(见图6)。由图5、图6可以发现，当采空区顶板厚度为7.2 m时，应属于Ⅰ类变形破坏；当厚度为12.0 m时，应属于Ⅲ类变形破坏。

同时，图5中顶板上部和侧翼未发生破坏，说明其“梯形拱”结构完好，而图6中顶板区域判定值Z分布均大幅小于0，表明顶板安全系数储备值过高。

因此，在实际开采过程中，采空区顶板的预留厚度应参照理论最小安全厚度值进行取值，合理平衡安全系数和回采率之间的关系。

图6  Z等值线彩云图(n=1.25，m=1.8)

Fig. 6  Color contour map for Z (n=1.25, m=1.8)

7) 讨论

上述计算过程中，没有考虑岩体内部成分的不均匀性和细小节理的影响，采空区顶板最终破坏形式可能发生局部变化。论文仅从宏观的角度进行分析，岩体内部参数的变化，不影响破坏变形的整体效应。同时，没有考虑采空区是分步形成的影响，没有考虑顶板不断受到爆破应力波作用，导致岩体内部结构可能出现累积损伤问题，这有待于后续深入研究。

3  影响机制分析

研究梅州地下石灰石矿三种破坏类型的内在机制，有利于定量分析各影响因素对顶板破坏作用。

由2.1节分析知，顶板的判定值Z峰值与顶板安全系数m、侧压系数k₀、跨厚比n等参数密切相关，为了对比分析，这里继续以该矿+35 m水平中段采空区为例，分别研究安全系数、侧压系数、跨厚比等因素对破坏类型的影响。

3.1  顶板安全系数m

为研究顶板安全系数对采空区顶板破坏类型可能的影响，在跨厚比n和侧压系数k₀既定的情况下，取不同顶板安全系数m进行分析。为揭示Ⅰ、Ⅱ、Ⅲ类等3种破坏类型的相互转化关系，通过试算对跨厚比进行取值。

限于篇幅，这里直接给出侧压系数和跨厚比取值结果，即侧压系数k₀=1.0，跨厚比n取值分别为1.5和3.0。根据《金属非金属矿山安全规程》^[23]的要求，采空区顶板安全系数须大于1.0，截取如图7所示反映变化的区域进行分析。

图7所示为顶板安全系数m与破坏类型影响关系图。其中图7(a)所示为Ⅰ、Ⅲ类破坏转化关系图，图7(b)所示为Ⅰ、Ⅱ类破坏转化关系图。

图7  顶板安全系数m与破坏类型影响关系图

Fig. 7  Influence of roof safety factor(m) on failure type

由图7(a)可以发现，在跨厚比和侧压系数既定的条件下，随着顶板安全系数不断增加，采空区顶板破坏类型由Ⅰ类转化为Ⅲ类，临界安全系数m=1.22；由图7(b)可以发现，在跨厚比和侧压系数既定的条件下，随着顶板安全系数不断增加，采空区顶板破坏类型由Ⅰ类转化为Ⅱ类，临界安全系数m=2.02。

因此，在跨厚比n和侧压系数k₀既定的条件下，顶板安全系数m仅影响Ⅰ、Ⅱ类或Ⅰ、Ⅲ类破坏类型之间的转化，在实际开采中顶板安全系数m属于可控因素。

3.2  跨厚比n

为研究跨厚比对采空区顶板破坏类型的影响，在顶板安全系数m和侧压系数k₀既定的情况下，取不同跨厚比n值进行分析。同理，经试算，这里给出顶板安全系数m为1.5，侧压系数k₀为1.0，跨厚比n取值范围为1.0~4.0情况下的关系图(见图8)。

图8所示为顶板跨厚比n与破坏类型影响关系图。由图8可以发现，在顶板安全系数和侧压系数既定的条件下，随着跨厚比不断增加，采空区顶板破坏类型由Ⅲ类转化为Ⅰ类，再转化为Ⅱ类。其中，Ⅲ类和Ⅰ类的临界跨厚比n=1.6，Ⅰ类和Ⅱ类的临界跨厚比n=3.5。

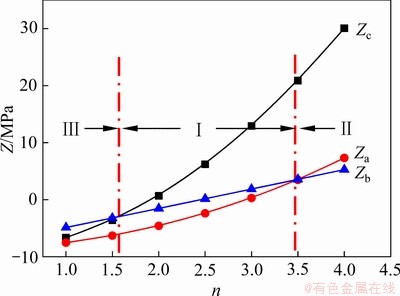
图8  顶板跨厚比n与破坏类型影响关系图

Fig. 8  Influence of roof span-thickness ratio (n) on failure type

因此，在顶板安全系数m和侧压系数k₀既定的条件下，跨厚比可以影响Ⅰ类、Ⅱ类、Ⅲ类等3种破坏类型之间的转化，在实际开采中跨厚比n属于可控因素。

3.3  侧压系数k₀

为研究侧压系数k₀对采空区顶板破坏型的影响，在顶板安全系数m和跨厚比n既定的情况下，取不同侧压系数进行分析。同理，经试算，这里顶板安全系数m取值为1.5，跨厚比n取值分别为1.2和2.4，侧压系数k₀取值范围为1.0~1.5(见图9)。

图9所示为顶板侧压系数k₀与破坏类型影响关系图。其中，图9(a)所示为Ⅰ、Ⅱ类破坏转化关系图，图9(b)所示为Ⅰ、Ⅲ类破坏转化关系图。

图9  顶板侧压系数k₀与破坏类型影响关系图

Fig. 9  Influence of roof lateral pressure factor (k₀) on failure type

由图9(a)可以发现，在顶板安全系数m和跨厚比n既定的条件下，随着侧压系数k₀不断增大，采空区顶板破坏类型由Ⅰ类转化为Ⅱ类，发生转化的临界侧压系数k₀=1.25。从图8(b)可以发现，在顶板安全系数和跨厚比既定的条件下，随着侧压系数不断增大，采空区顶板破坏类型由Ⅰ类转化为Ⅲ类，发生转化的临界侧压系数k₀=1.33。

综上所述，在跨厚比n和顶板安全系数m既定的条件下，侧压系数k₀仅影响Ⅰ、Ⅱ类或Ⅰ、Ⅲ类顶板破坏类型之间的转化。

由于侧压系数k₀与采空区岩层构造、埋深等因素有关，属于不可控因素。

4  工程实例验证

根据矿山初步设计资料，该矿山+35 m、+7 m水平中段采空区顶板设计预留厚度15.0 m，跨度为15.0 m。这里利用式(10)对顶板参数进行计算分析。

若顶板跨度保持不变，顶板安全系数m=1.8，侧压系数取k₀=1.0。此时，必须满足Z_a＜0，Z_b＜0。经计算，+35 m、+7 m水平中段采空区顶板最小理论安全厚度分别为7.2 m和8.5 m。

由于+35 m水平中段石灰石矿体质量好、品位高，其中5^#~8^#采空采场出现超采问题，顶板实际预留厚度为8.0~9.0 m，经计算，仍然满足理论最小安全厚度要求。

1) 对于+35 m水平中段采空区，当顶板厚度 7.2 m时，由式(10)计算知，Z_b=0 MPa，Z_a=-3.00 MPa，Z_c=3.45 MPa，即Z_a＜Z_b＜Z_c，应属于一类变形破坏；当顶板厚度为15.0 m时，Z_b=-4.32 MPa，Z_a=-7.14 MPa，Z_c=-6.62 MPa，即Z_a＜Z_c＜Z_b，可能属于Ⅲ类变形破坏。

2) 对于+7 m水平中段采空区，当顶板厚度8.5 m时，由式(9)计算知，Z_b=0 MPa，Z_a=-3.91 MPa，Z_c=0.623 MPa，即Z_a＜Z_b＜Z_c，岩体应属于Ⅰ类变形破坏；当顶板厚度为15.0 m时，Z_b=-3.19 MPa，Z_a=-6.85 MPa，Z_c=-6.49 MPa，即Z_a＜Z_c＜Z_b，可能属于Ⅲ类变形破坏。

为了验证计算结果，对+35 m、+7 m水平中段采空区进行实地考察，图10(a)所示为+7 m水平中段3^#采空区顶板实景图，由于顶板厚大，该采空区形成后始终保持稳定，现场未发现“梯形拱”冒落现象。图10(b)所示为+35 m水平中段7^#采空区顶板冒落实景图，采空区形成初期顶板局部发生冒落现象，但在形成“梯形拱”后保持整体稳定。

+7 m水平中段1^#、2^#、4^#采空区与3^#采空区相似，稳定程度很高。+35 m水平中段5^#、6^#采空区观察到了“梯形拱”，8^#采空区仅观察到了少量落石现象。

综上现场勘察结果可以判断，顶板的“梯形拱”效应和理论最小安全厚度计算结果基本合理。

图10  采空区顶板冒落实景图

Fig. 10  Roof caving in goaf

5  结论

1) 在梅州某石灰岩采空区调研的基础上，构建水平层状优势节理顶板力学模型，推导了其应力分量表达式；结合Mohr-Coulomb岩体强度准则，给出了任意点岩体破坏判定值Z及其峰值的数学式；依据判定值Z峰值大小排序，分析了顶板可能出现的脱落型(Ⅰ类)、挠曲型(Ⅱ类)、剪切型(Ⅲ类)等3种破坏类型及特征。

2) 采空区顶板Z峰值计算结果表明，位于顶部、下部、两侧翼等位置出现4个峰值区域，顶板可能存在Ⅰ、Ⅱ、Ⅲ类等变形破坏。在Ⅰ、Ⅱ类变形破坏过程中，顶板具有“梯形拱”承载效应；在Ⅲ类破坏过程中，顶板具有类似“工”型承载特征。

3) 顶板破坏类型受顶板安全系数m、跨厚比n和侧压系数k₀等因素影响，m和n为可控因素，k₀为不可控因素。当k₀和n既定时，m仅影响Ⅰ、Ⅱ类或Ⅰ、Ⅲ类间转化变形破坏，临界处m分别为2.02和1.22；k₀影响方式与m的影响情况相似，临界处k₀分别为1.25和1.33。当m和k₀既定时，n影响Ⅰ、Ⅱ、Ⅲ类等3种变形破坏类型之间的转化，临界处n为1.6和3.5。

4) 该矿山+35 m、+7 m水平中段采空区实地勘察表明，1^#~4^#采空区顶板(厚度约15.0 m)符合Ⅲ类破坏特征，采空区基本稳定；5^#~8^#采空区顶板(厚度8.0~9.0 m)符合Ⅰ类变形破坏特征，存在“梯形拱”效应。现场情况验证了理论计算结果的合理性。

REFERENCES

[1] ALAIN D, GILLES F, OLIVIER L, et al. Influence of geomorphological constraints and exploitation techniques on stone quarry spatial organisation: Example of Lutetian underground quarries in Rheims, Laon and Soissons areas[J]. Engineering Geology, 2010, 115(3/4): 268-275.

[2] 姜立春, 曾俊佳, 王国伟. 水平采空区群离散多自由度动力响应模型[J]. 岩石力学与工程学报, 2016, 35(1): 59-67.

JIANG Li-chun, ZENG Jun-jia, WANG Guo-wei. A discrete dynamic response model with multiple degrees of freedom for horizontal goaf group[J]. Chinese Journal of Rock Mechanics and Engineering, 2016, 35(1): 59-67.

[3] 姜立春, 苏 勇. 胶结充填体矿柱失稳的临界爆破振速理论模型及应用[J]. 中国有色金属学报, 2019, 29(11): 2663-2670.

JIANG Li-chun, SU Yong. Theoretical model and application of critical blasting vibration velocity for instability of cemented backfill pillar[J]. The Chinese Journal of Nonferrous Metals, 2019, 29(11): 2663-2670.

[4] 吴爱祥, 沈慧明, 姜立春, 等. 窄长型充填体的拱架效应及其对目标强度的影响[J]. 中国有色金属学报, 2016, 26(3): 648-654.

WU Ai-xiang, SHEN Hui-ming, JIANG Li-chun, et al. Arching effect of long-narrow cemented pastebackfill body and its effect on target strength[J]. The Chinese Journal of Nonferrous Metals, 2016 26(3): 648-654.

[5] MA Hai-tao, WANG Ji-nan, WANG Yun-hai. Study on mechanics and domino effect of large-scale goaf cave-in[J]. Safety Science, 2012, 50(4): 689-694.

[6] FU J X, SONG W D, DU J H. Study of disturbance law for wall rock while goaf group formation in metal mines[J]. Rock and Soil Mechanics, 2013, 34(S1): 508-515.

[7] 陈庆发, 牛文静, 郑文师, 等. 崩落法回采巷道顶板危险区域确定的解构法和数值模拟法[J]. 中国有色金属学报, 2017, 27(5): 1006-1015.

CHEN Qing-fa, NIU Wen-jing, ZHENG Wen-shi, et al. Deconstruction method and numerical simulation method of determination of tunnel roof’s dangerous area in caving stoping process[J]. The Chinese Journal of Nonferrous Metals, 2017, 27(5): 1006-1015.

[8] MURPHY M M, ELLENBERGER J L, ESTERHUIZEN G S, et al. Analysis of roof and pillar failure associated with weak floor at a limestone mine[J]. International Journal of Mining Science and Technology, 2016 26(3): 471-476.

[9] 张敏思, 朱万成, 侯召松, 等. 空区顶板安全厚度和临界跨度确定的数值模拟[J]. 采矿与安全工程学报, 2012, 29(4): 543-548.

ZHANG Min-si, ZHU Wan-cheng, HOU Zhao-song, et al. Numerical simulation for determining the safe roof thickness and critical goaf span[J]. Journal of Mining & Safety Engineering, 2012, 29(4): 543-548.

[10] 姜立春, 王玉丹. 复杂荷载作用下残采矿柱综合安全系 数[J]. 中南大学学报(自然科学版), 2018, 49(6): 1511-1518.

JIANG Li-chun, WANG Yu-dan. Comprehensive safety factor of residual mining pillar under complex loads[J]. Journal of Central South University (Science and Technology), 2018, 49(6): 1511-1518.

[11] 姜立春, 陈 鹏, 吴爱祥. 基于不同充填接顶率的采空区顶板拱架自稳效应[J]. 中国有色金属学报, 2019, 29(1): 187-193.

JIANG Li-chun, CHEN Peng, WU Ai-xiang. Roof self-stabilizing arching effect of goaf based on different roof-contacted filling rate[J]. The Chinese Journal of Nonferrous Metals, 2019, 29(1): 187-193.

[12] BRADY B H G, BROWN E T. Rock Mechanics for underground mining[M]. London: Allen and Unwin, 1985.

[13] 陈 虎, 叶义成, 王其虎, 等. 基于岩梁-块体理论的巷道软弱层直接顶板破坏形式研究[J]. 岩土力学, 2020, 41(4): 1447-1454.

CHEN Hu, YE Yi-cheng, WANG Qi-hu, et al. Study on direct roof failure form of soft layer in roadway based on rock beam-block theory[J]. Rock and Soil Mechanics, 2020, 41(4): 1-8.

[14] 许家林. 岩层控制与煤炭科学开采—— 记钱鸣高院士的学术思想和科研成就[J]. 采矿与安全工程学报, 2019, 36(1): 5-10.

XU Jia-lin. Strata control and scientific coal mining—A celebration of the academic thoughts and achievements of Academician Minggao Qian[J]. Journal of Mining & Safety Engineering, 2019, 36(1): 5-10.

[15] DENG J, GU D S. Buckling mechanism of pillar rockbursts in underground hard rock mining[J]. Geomechanics and Geoengineering, 2018, 13(3): 168-183.

[16] 谢学斌, 邓融宁, 董宪久, 等. 基于突变和流变理论的采空区群系统稳定性[J]. 岩土力学, 2018, 39(6): 1963-1971.

XIE Xue-bin, DENG Rong-ning, DONG Xian-jiu, et al. Stability of goaf group system based on catastrophe theory and rheological theory[J]. Rock and Soil Mechanics, 2018, 39(6): 1963-1971.

[17] YU L, LIU J. Stability of interbed for salt cavern gas storage in solution mining considering cusp displacement catastrophe theory[J]. Petroleum, 2015, 1(3): 82-90.

[18] 狄圣杰, 徐卫亚, 王 伟, 等. 柱状节理岩体横观各向同性本构关系研究[J]. 中国矿业大学学报, 2011, 40(6): 50-56.

DI Sheng-jie, XU Wei-ya, WANG Wei, et al. Transversely isotropic constitute properties of a columnar jointed rock mass[J]. Journal of China University of Mining & Technology, 2011, 40(6): 50-56.

[19] 鲁海峰, 姚多喜. 采动底板层状岩体应力分布规律及破坏深度研究[J]. 岩石力学与工程学报, 2014, 33(10): 2030-2039.

LU Hai-feng, YAO Duo-xi. Stress distribution and failure depth of layered rock mass of mining floor[J]. Chinese Journal of Rock Mechanics and Engineering, 2014, 33(10): 2030-2039.

[20] RUKHAIYAR S, SAMADHIYA N K. Triaxial strength behaviour of rockmass satisfying Modified Mohr-Coulomb and Generalized Hoek-Brown criteria[J]. International Journal of Mining Science and Technology, 2018, 28(6): 901-915.

[21] 罗斌玉, 叶义成, 李玉飞, 等. Mohr-Coulomb准则下倾斜矿柱稳定性的安全系数法[J]. 煤炭学报, 2018, 43(9): 46-53.

LUO Bin-yu, YE Yi-cheng, LI Yu-fei1, et al. Safety factor method for stability of inclined pillars under Mohr-Coulomb criterion[J]. Journal of China Coal Society, 2018, 43(9): 46-53.

[22] 陈 国, 张齐生, 黄东升, 等. 腹板开洞竹木工字梁受力性能的试验研究[J]. 湖南大学学报(自然科学版), 2015, 42(11): 111-118.

CHEN Guo, ZHANG Qi-sheng, HUANG Dong-sheng, et al. Experimental study on mechanical performance of OSB webbed bamboo I shaped joist with web openings[J]. Journal of Hunan University(Natural Sciences), 2015, 42(11): 111-118.

[23] GB 16423—2006. 金属非金属矿山安全规程[S].

GB 16423—2006. Safety regulations for metal and nonmetal mines[S].

Roof failure characteristics and its influence mechanism in limestone goaf with horizontal layered dominant joints

JIANG Li-chun^{1, 2}, ZHANG Hao², WANG Jian-de³

(1. Institute of Safety Science and Engineering, South China University of Technology, Guangzhou 510640, China;

2. School of Civil Engineering and Transportation, South China University of Technology, Guangzhou 510640, China;

3. Guangdong Academy of Safety Science and Technology, Guangzhou 510640, China)

Abstract: In order to study the failure characteristics and influence mechanism of the roof of goaf in layered limestone mine, based on the investigation of a underground limestone mine in Meizhou, a mechanical model of the roof with horizontal layered dominant joints was built, and the expressions of stress components were derived. Combined with the M-C strength criterion of rock mass, the failure judgment value Z at any point in roof and its peak value mathematical formula were given, and the possible failure type and deformation characteristics in instability process were analyzed. The results indicate that, there are four peak areas at the top, the bottom and both sides of the roof. According to the order of peak values of Z, there are three kinds of possible deformation failure forms, spalling type (Ⅰ), deflet type (Ⅱ) and shear type (Ⅲ). In class Ⅰ or class Ⅱ failures, the roof has the bearing effect of trapezoid arch; in class Ⅲ failure, the roof has the bearing effect similar to I-beam. The failure type of roof is affected by some factors, such as safety factor(m), span-thickness ratio(n) and lateral pressure factor(k₀). m and n are controllable factors, and k₀ is uncontrollable factors. When k₀ and n are definite, m only affects the transformation between class Ⅰ and class Ⅱ or class Ⅰ and class Ⅲ failures, and the critical values of m are 2.02 and 1.22. When m and n are definite, k₀ affects the same way as m, and the critical values of m are 1.25 and 1.33. When k₀ and m are definite, n affects the transformation between class Ⅰ, Ⅱ and Ⅲ failures, and the critical values of m are 1.6 and 3.5. The results of field investigation of goaf verify the rationality of theoretical analysis results. The results provide theoretical basis for the selection of roof parameters in goaf of such mines.

Key words: limestone goaf; types of deformation and failure; influence mechanism; roof safety factor; span-thickness ratio

Foundation item: Project(51974135) supported by the National Natural Science Foundation of China; Project (2016YFC0600802) State Key Research Development Program of China; Project (2019-XMZC-0009-04) supported by Special Project of Disaster Prevention and Emergency Management in Guangdong Province, China

Received date: 2020-03-27; Accepted date: 2020-08-31

Corresponding author: JIANG Li-chun; Tel: +86-20-87111039; E-mail: ginger@scut.edu.cn

(编辑  王  超)

基金项目：国家自然科学基金资助项目(51974135)；国家重点研发计划资助项目(2016YFC0600802)；广东省灾害防治及应急管理专项(2019-XMZC-0009-04)

收稿日期：2020-03-27；修订日期：2020-08-31

通信作者：姜立春，教授，博士；电话：020-87111039；E-mail：ginger@scut.edu.cn