DOI: 10.11817/j.issn.1672-7207.2017.05.033
搅拌对冰浆存储冰晶粒径演化的影响
唐艺芳1,刘志强1, 2,王肖肖1,康威1,张静雅1
(1. 中南大学 能源科学与工程学院,湖南 长沙,410083;
2. 湖南省建筑节能与环境控制关键技术协同创新中心,湖南 株洲,412007)
摘要:为研究搅拌作用下冰浆存储过程中冰晶粒径演化的规律,基于冰晶动力学事件核模型,利用Fluent软件、耦合多相流模型与数群平衡模型对冰浆存储过程中冰晶粒径演化进行模拟,将平均粒径模拟值与实验值进行对比分析,并对模型有效性进行验证。基于修正的冰晶动力学事件核模型对搅拌作用下冰浆存储过程中的冰晶粒径演化进行模拟,分析单螺旋桨桨叶直径及位置、双螺旋桨桨叶间距对冰浆存储过程中冰晶体积分数分布、冰晶粒径数量密度分布及冰晶平均粒径演化的影响。研究结果表明:桨叶直径对冰晶体积分数分布、冰晶粒径数量密度分布及冰晶平均粒径均有影响;桨叶间距对冰晶体积分数分布影响显著;双螺旋桨能够使蓄冰槽内冰晶分布更加均匀,更能抑制冰晶粒径增长。
关键词:储能;冰浆;多相流模型;数群平衡模型
中图分类号:TB65 文献标志码:A 文章编号:1672-7207(2017)05-1376-08
Effects of stirring action on ice crystal size evolution during storage
TANG Yifang1, LIU Zhiqiang1, 2, WANG Xiaoxiao1, KANG Wei1, ZHANG Jingya1
(1. School of Energy Science and Engineering, Central South University, Changsha 410083, China;
2. Collaborative Innovation Center of Building Energy Conservation & Environmental Control, Zhuzhou, 412007, China)
Abstract: In order to study the evolution of ice crystal size with stirring action during the process of ice slurry storage, the multiphase flow model and the population balance model (PBM) were coupled to simulate the evolution of ice crystal size based on the ice crystal event nucleus models. The ice crystal event nuclear model parameters were modified based on the comparison of numerical results and experiment results. The effects of the stirring action on the evolution of ice crystal size were studied by analyzing the effect of the blade size and position of single screw, the blade spacing of twin screw on the volume fraction distribution of ice crystal, number density of ice crystal size and average particle size. The results show that the blade size has influence on volume fraction distribution of ice crystal, number density of ice crystal size and average particle size, and the blade position and spacing have significant influence on volume fraction distribution. Twin screw can make the distribution of ice crystal more uniform in the storage tank, and can be more effective to inhibit the growth of ice crystal size.
Key words: energy storage; ice slurry; multiphase flow model; population balance model
冰浆是由载流溶液和冰晶组成的固液两相流,具有流动与传热特性良好、蓄能密度大、无污染等优点,现已应用于区域供冷、蓄冷空调系统及工业冷却等领域,且在化工、医药、环保等领域具有广阔的应用前景[1]。冰浆在存储过程中,在成核、生长、破碎、团聚等作用下,冰晶粒径及分布会随着时间发生变化。冰晶粒径及分布对冰浆流动与换热特性有重要影响,如冰晶的富集容易导致冰浆释冷速度慢且不能完全融化、泵送困难等问题[2-4],人们对冰晶粒径控制等方面进行了研究,目前研究主要集中在冰晶粒径生长抑制添加剂种类及浓度方面,冰浆存储过程特性研究则主要集中在冰浆的富集与分层等宏观方面[5-8]。DELAHAYE等[9]采取向蓄冰槽内通入空气的措施抑制冰晶富集,但该方法容易造成设备腐蚀。加入添加剂溶液能抑制冰晶聚集增长,但会明显降低溶液冷凝温度。而在蓄冰槽中增加扰动能够有效地抑制冰晶聚集,同时又不会引起腐蚀设备与降低溶液冷凝温度等问题[3],因此,螺旋桨搅拌得到了较广泛应用。目前,基于微观层面对冰晶粒径演化已有少量研究。PRONK等[10-11]运用结晶动力学理论对冰浆存储过程冰晶粒径演化机理进行理论分析和实验研究,理论上认为冰晶粒径分布主要是Ostwald熟化作用的结果[3]。赵腾磊等[12-13]运用数群平衡模型研究了破碎与团聚对冰浆存储过程冰晶粒径演化的影响,但均未考虑存储方式及空间等因素的影响。目前,基于微观层面的冰晶粒径演化的研究较少,且已有的冰晶聚集核模型及破碎核模型的理论计算结果与实验结果之间仍存在明显差异。数群平衡模型(population balance model, PBM)是模拟离散系统中离散单元动力学演化过程的有效方法[14],本文综合考虑冰晶的成核、生长、团聚及破碎等微观动力学行为,基于已有的冰晶动力学事件核模型建立冰晶数群平衡模型,耦合多相流模型与数群平衡模型对冰浆存储过程中冰晶粒径演化进行数值模拟,并对模型的有效性进行验证,最后着重分析单螺旋桨桨叶直径及位置、双螺旋桨桨叶间距对冰浆存储过程中冰晶体积分数分布、冰晶粒径数量密度分布及冰晶平均粒径演化的影响。
1 模型
1.1 多相流模型
冰浆在存储过程中,冰晶粒子悬浮在溶液中,不会发生两相完全分层的现象,故选用Euler模型描述冰浆流动。
1.2 冰晶动力学事件核模型
1.2.1 冰晶成核模型
MICHAEL等[3,15]对冰晶初次成核进行了理论分析与实验研究,得出冰晶初次成核率J的计算式为
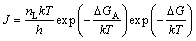 (1)
(1)
同质成核时,△G的表达式为
 (2)
(2)
异质成核时,△G的表达式为
 (3)
(3)
式中:nL为单位体积内分子数;k为波尔兹曼常数,J/K;T为溶液热力学温度,K;h为普朗克常数,J·s;△GA为水分子活化能,J/kg;△G为成核能,J/kg;γiw为冰水之间表面能,mJ/m2;Teq为溶液相变平衡热力学温度,K;ρice为冰晶的密度,kg/m3;hf 为凝固潜热,J/kg;△T为过冷度,K;f(m,R′)为晶核在异质基体表面的接触角、异质基体粒度与临界晶核粒度之比的函数。
1.2.2 冰晶生长核模型
目前应用较多的是PRONK[16]提出的计算冰晶生长率模型,该模型能较准确地计算冰晶的生长率G:
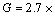
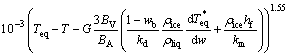 (4)
(4)
式中:BV和BA分别为体积常数和面积常数;wb为溶液中水的质量分数,%;kd为质量传递常数,m/s;ρlid为溶液密度,kg/m3;km为热量传递函数,W/(m2·K)。
1.2.3 冰晶聚集核模型
用布朗聚集核模型表示体积为V的颗粒团聚为体积为 的速率表达式为
的速率表达式为
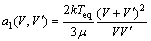 (5)
(5)
式中:μ为冰浆中载流溶液的动力黏度,Pa·s。
1.2.4 冰晶破碎核模型
粒子的破碎受到机械搅动、溶液物性等因素影响,可用下式计算冰晶的破碎率[17]:
 (6)
(6)
式中: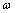 为含冰率;C1和C2为常数,分别取0.004 81和0.080 00;δ为表面张力,J/m2;ρl为溶液密度,kg/m3;ε为扩散耗损率,W/kg;d为冰晶粒径,μm。本文所研究的冰晶破碎为母冰晶破碎成2个子冰晶,体积为
为含冰率;C1和C2为常数,分别取0.004 81和0.080 00;δ为表面张力,J/m2;ρl为溶液密度,kg/m3;ε为扩散耗损率,W/kg;d为冰晶粒径,μm。本文所研究的冰晶破碎为母冰晶破碎成2个子冰晶,体积为 的粒子破碎成体积为V的概率为
的粒子破碎成体积为V的概率为
 (7)
(7)
式中:c为粒子的形状因子,本文假设粒子为球形,即c=1。
2 模型验证
基于PRONK的冰浆存储实验[8]对模型进行验证。依据其中实验3,建立无搅拌蓄冰槽数值模型,直径为640 mm、高为860 mm的圆柱形蓄冰槽内为非均匀存储的冰浆溶液。依据其中实验13,建立有搅拌蓄冰槽数值模型,直径为125 mm、高为130 mm的圆柱形蓄冰槽内为均匀存储的冰浆溶液,蓄冰槽内配备有螺旋桨搅拌器。分别选用颗粒动力学理论模型、标准k-ε混合湍流模型描述冰晶粒子间的相互作用及冰浆湍流作用,建立流体力学模型。
2.1 模拟条件
根据实验条件对模型物性参数进行设置,冰浆的物性参数如表1所示。
表1 冰浆的物性参数
Table 1 Physical parameters of ice slurry solutions

2.1.1 边界条件
1) 假设冰浆存储过程中与外界没有质量和能量交换,蓄冰槽壁面可以认为是理想绝热壁面。2) 假设冰晶成核发生在最小粒径处,添加剂为乙醇、氯化钠时,冰晶粒径计算区域分别取0.01~900 μm和0.01~1 200 μm。不计计算区域以外的冰晶颗粒,即假设在计算区域以外的冰晶粒径数量密度为0 个/m4。
2.1.2 初始条件
1) 假设初始时刻每个空间网格节点处冰晶粒径分布相同,将实验测定的冰晶粒径分布进行拟合得到初始时刻冰晶粒径数量密度的对数正态分布的数学表达式如下:
 (8)
(8)
式中:x为冰晶粒径,μm;x0为初始时刻冰晶平均粒径,μm。x0根据实验结果给定,实验3、实验13中初始时刻冰晶平均粒径分别为97 μm和207 μm。
2) 假定冰晶在粒径最小处的成核率为1 m-3/s。冰晶的生长率与冰晶粒径相关,但在同一种添加剂溶液、过冷度一定的条件下其变化不大,故假设不同粒径的冰晶生长率相同,为10-10 m/s。
2.2 模型验证
冰晶在布朗扩散作用下会发生碰撞导致破碎,粒径越大,其破碎作用越明显,故应考虑布朗扩散的破碎作用,引入布朗扩散耗损率ε0。布朗扩散作用下破碎率公式为
 (9)
(9)
式中:ε0为布朗扩散耗损率,其值为0.000 1 W/kg。
通过选用合适的参数,得到无搅拌作用下冰浆存储2 h后冰晶平均粒径实验拟合曲线与数值模拟曲线,如图1所示。从图1可见:冰晶平均粒径实验拟合曲线与数值模拟曲线基本吻合,验证了模型的有效性。
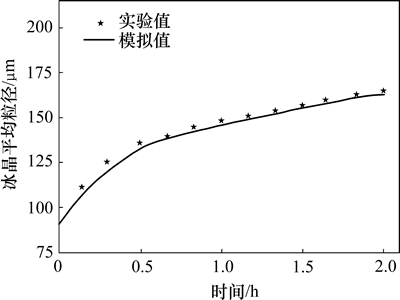
图1 无搅拌作用下冰浆存储2 h后冰晶平均粒径演化的实验拟合结果与数值模拟结果
Fig. 1 Average particle size after 2 h storage with no stirring action obtained by model and experiment
在搅拌作用下,冰晶的聚集受布朗作用与湍流作用影响,故应考虑湍流聚集率,引入湍流聚集参数C3。
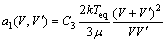 (10)
(10)
通过选用合适的破碎率参数及湍流聚集参数,得到搅拌作用下冰浆存储2 h后冰晶平均粒径演化实验拟合曲线与数值模拟曲线如图2所示,可见两者吻合较好,进一步验证了模型的有效性。
聚集核模型和破碎核模型的选用参数如下:破碎参数C1为4.81×10-6;破碎参数C2为0.080 0;湍流聚集参数C3为0.030 9。

图2 搅拌作用下冰浆存储2 h后冰晶平均粒径演化的实验拟合结果与数值模拟结果
Fig. 2 Average particle size after 2 h storage with stirring action obtained by model and experiment
3 结果与分析
3.1 单螺旋桨对冰浆存储的影响
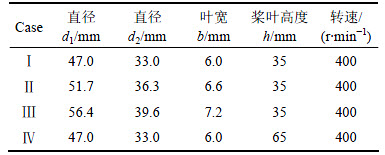
按螺旋桨桨叶直径、位置不同,设置CaseⅠ~ Case Ⅳ共4种桨叶参数,见表2。
表2 单螺旋桨参数
Table 2 Parameters of single propeller
3.1.1 桨叶直径对冰浆存储的影响
在CaseⅠ,Case Ⅱ和Case Ⅲ下,当存储时间分别为1.5 h和3.0 h时蓄冰槽内冰晶体积分数分布见图3。
从图3可见:现桨叶直径越大,蓄冰槽上部和桨叶下边缘冰晶体积分数越小,蓄冰槽底部冰晶体积分数越大,顶部和底部冰晶体积分数之差越小。由于桨叶直径越大,其旋转造成周围流体的流动越剧烈且扰动范围越大,冰晶向上的流动速度随之增大,冰晶粒子的破碎作用显著增强,因此,蓄冰槽上部冰晶粒子数量会随桨叶直径增大而增大,但冰晶总体积反而减小,冰晶富集现象减弱。
在Case Ⅰ,Case Ⅱ和Case Ⅲ下,冰晶粒径数量密度分布曲线见图4。从图4可知:桨叶直径不同,但冰晶数量密度分布曲线均类似于对数正态分布曲线,且随时间逐渐向右推移,出现由“高窄”到“矮宽”的变化,只是推移的程度不同。对比存储时间t= 3 h可发现:桨叶直径越大,同时刻小粒径冰晶数量密度越大,大粒径冰晶数量密度越小;冰晶粒径数量密度的峰值越大,其数量密度峰值对应的粒径越小;当桨叶直径增大时,冰晶粒径数量密度分布曲线向右推移会出现迟缓现象,且桨叶直径越大,迟缓现象越严重。这是由于桨叶直径越大其扰动作用越强,冰晶粒子之间、粒子与蓄冰槽壁面的碰撞概率及能量越大,冰晶碰撞后破碎概率也就越大,因此,螺旋桨桨叶直径越大,冰晶粒子破碎作用越强。但聚集作用始终大于破碎作用,只是两者之差会逐渐减小。由此可见,增大桨叶直径能够增强对冰晶粒径增长的抑制作用。

图3 CaseⅠ~Case Ⅲ冰晶体积分数分布
Fig. 3 Particle volume fraction distributions of CaseⅠ to Case Ⅲ

图4 CaseⅠ~Case Ⅲ冰晶粒径数量密度分布演化曲线
Fig. 4 Curves of particle number density distributions for CaseⅠ to Case Ⅲ
在Case Ⅰ,Case Ⅱ和Case Ⅲ下,冰晶平均粒径随存储时间的变化见图5。从图5可知:冰晶平均粒径随时间逐渐增大,但增长速率随时间逐渐减小。这主要是因为在冰浆储存初期,蓄冰槽内冰晶粒径较小,此时,冰晶粒子的聚集速率较大,破碎速率较小,所以,冰晶的粒径迅速增大;而存储时间越长,冰晶粒径在逐渐增大的同时其破碎速率迅速增大,导致冰晶粒子聚集作用与破碎作用之差逐渐减小,因此,冰晶粒径会增大,但增大速率逐渐降低。经对比可知:桨叶直径越大,冰晶的平均粒径越小,验证了增大桨叶直径能够抑制冰晶粒径增大,且桨叶直径越大,其抑制作用越强。

图5 CaseⅠ~ Case Ⅲ冰晶平均粒径与时间的关系
Fig. 5 Relationship between average particle size and time for CaseⅠ to Case Ⅲ
3.1.2 桨叶位置对冰浆存储的的影响
在Case Ⅳ下,当蓄冰槽内存储时间为1.5 h和3.0 h时冰晶体积分数分布见图6。对比图6与图3可知:桨叶距蓄冰槽底部高度h越大,蓄冰槽上部冰晶粒子体积分数越小,底部冰晶体积分数越大,冰晶富集现象越轻微。这是由于扰动区域越接近冰晶堆积区域,更能够削弱富冰层的形成,且由于冰晶流动在桨叶上部均会形成旋涡,h越大,旋涡越大,旋涡处冰晶流速越大,冰晶越不容易向上流动,故螺旋桨周围冰晶粒子体积分数均呈现上少下多的分布情况;随h增大,其桨叶上下浓度差值变小且冰晶富集分布区域变小。
在CaseⅠ和Case Ⅳ下,冰晶粒径数量密度分布见图7。从图7可知:冰晶数量密度分布曲线均随时间向右推移,出现由“高窄”变为“矮胖”的现象,以t=3 h为例,冰晶粒径数量密度分布曲线几乎重合。这是由于当h变化、桨叶直径不变只会引起扰动区域变化,而扰动强度不变,故冰晶动力学事件的发生速率基本没有变化。可见:桨叶位置的改变主要引起冰晶粒径在空间分布上不同,而对冰晶数量密度分布影响很小。
在CaseⅠ和Case Ⅳ下,冰晶平均粒径随存储时间的变化见图8。从图8可见:桨叶高度h不同,冰晶平均粒径均随时间而逐渐增大,但平均粒径随时间的变化曲线几乎重叠,故h的变化对冰晶平均粒径的影响很小。

图6 Case Ⅳ冰晶体积分数分布
Fig. 6 Particle volume fraction distributions of Case Ⅳ

图7 CaseⅠ及Case Ⅳ冰晶粒径数量密度演化曲线
Fig. 7 Relationship between particle number density distributions and time for CaseⅠ and Case Ⅳ

图8 CaseⅠ及Case Ⅳ冰晶平均粒径演化曲线
Fig. 8 Curves of average particle size with time for CaseⅠ and Case Ⅳ
3.1.3 双螺旋桨对冰浆存储影响分析
按螺旋桨桨叶间距不同,设置CaseⅤ,CaseⅥ和CaseⅦ这3种桨叶参数,见表3。
表3 双螺旋桨参数
Table 3 Parameters of twin propellers

3.1.4 桨叶间距对冰浆存储的影响
在Case Ⅴ,Case Ⅵ和Case Ⅶ下,存储时间分别为1.5 h和3.0 h时蓄冰槽内冰晶体积分数分布见图9。由图9可知:在双螺旋浆搅拌下,冰晶体积分数在蓄冰槽顶部和桨叶下边缘比较大,在蓄冰槽底部和桨叶上边缘比较小;下桨叶下边缘更容易产生冰晶堆积,且下桨叶上、下边缘冰晶体积分数差值较上桨叶大。由此可以看出:螺旋桨旋转在一定程度上抑制了冰晶向上部堆积,下桨叶会阻止一部分冰晶在上桨叶下边缘聚集;在同一时刻,桨叶间距h1不同,蓄冰槽内冰晶体积分数分布大体一致,蓄冰槽顶部和底部冰晶体积分数之差先随桨叶间距增大而减小,随着桨叶间距继续增大,其值反而增大。由于桨叶间距越大,对蓄冰槽上、下部冰浆的搅拌作用越强,但对蓄冰槽中部搅拌作用减弱,导致蓄冰槽内冰晶体积分数分布均匀性先随桨叶间距增大而越来越好,当桨叶间距达到某一值后冰晶体积分数分布均匀性反而越来越差。因此,存在1个最佳的桨叶间距h1使蓄冰槽内冰晶分布均匀。

图9 Case Ⅴ~ Case Ⅶ冰晶体积分数分布
Fig. 9 Particle volume fraction distributions of Case Ⅴ to Case Ⅶ
Case Ⅴ,Case Ⅵ和Case Ⅶ下冰晶粒径数量密度分布见图10。从图10可知:冰晶数量密度分布曲线均类似于对数正态分布,随时间向右推移,出现由“高窄”变为“矮宽”的现象。与t=3 h时对比发现不同桨叶间距下冰晶粒径数量密度分布曲线几乎重叠。这是由于桨叶间距h1的变化主要引起搅拌区域发生变化,影响冰晶在蓄冰槽内的空间分布,而对扰动强度、冰晶粒子总的聚集作用和破碎作用几乎没有影响。
在Case Ⅴ,Case Ⅵ和 Case Ⅶ下冰晶平均粒径随存储时间的变化见图11。从图11可见:冰晶平均粒径均随时间逐渐增大,其增长速率随时间逐渐减小;桨叶间距h1不同,冰晶平均粒径随时间变化曲线几乎重合,表明h1对于冰晶平均粒径演化几乎没有影响。

图10 Case Ⅴ~Case Ⅶ冰晶粒径数量密度演化曲线
Fig. 10 Curves of particle number density distributions in time Case Ⅴ to Case Ⅶ

图11 Case Ⅴ~Case Ⅶ冰晶平均粒径粒径演化曲线
Fig. 11 Curves of average particle size for CaseⅤ to Case Ⅶ
3.2 单、双螺旋桨对冰浆存储影响的对比分析
选取桨叶直径相同、冰晶分布均匀性最好的Case Ⅳ与Case Ⅵ,对比图6中 Case Ⅳ与图9中 Case Ⅵ的冰晶体积分数分布发现:由于双螺旋桨增大了扰动强度和扰动区域,对冰晶粒子的破碎作用增强,使得双螺旋桨蓄冰槽内冰晶数量更大,但每个冰晶粒子的体积会比较小,双螺旋桨蓄冰槽内冰晶总体积比较小,有效地抑制冰晶因受到升力等作用向上运动形成富冰层的趋势,因此,双桨叶螺旋能够使蓄冰槽内冰晶分布更加均匀。
在Case Ⅳ和Case Ⅵ下,冰晶粒径数量密度分布见图12。从图12可知:冰晶数量密度分布曲线均随时间向右推移,经过相同时间其推移量不同。与单螺旋桨相比,由于双螺旋桨有效地增大了扰动强度和扰动区域,双桨叶螺旋桨蓄冰槽内小粒径冰晶数量密度随时间的减小量和大粒径冰晶粒径数量密度增加量均较小,同一时刻冰晶粒径数量密度峰值较大,峰值对应的冰晶粒径比较小。因此,增加桨叶个数能够起到抑制冰晶生长的作用。
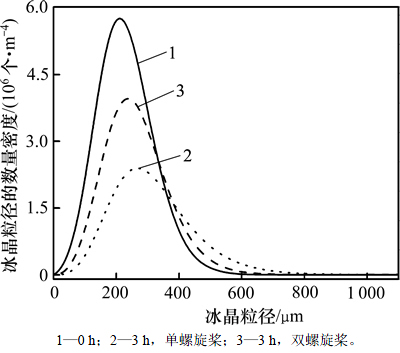
图12 Case Ⅳ及Case Ⅵ冰晶粒径数量密度分布演化曲线
Fig. 12 Curves of particle number density distributions for Case Ⅳ and Case Ⅵ
单、双螺旋桨蓄冰槽内冰晶平均粒径随存储时间的变化见图13。从图13可见:单、双螺旋桨蓄冰槽内冰晶平均粒径均随时间逐渐增大;与单螺旋桨相比,双螺旋桨蓄冰槽中冰晶平均粒径及其增长速率均较小。其原因是双桨叶螺旋桨对冰浆的扰动强度及区域均比单桨叶螺旋桨的大,因此,对冰晶粒径增长的抑制作用越强,冰晶越不容易长大。

图13 Case Ⅳ及Case Ⅵ冰晶平均粒径演化曲线
Fig. 13 Curves of average particle size for Case Ⅴ and Case Ⅶ
4 结论
1) 单螺旋桨桨叶直径对蓄冰槽内冰晶体积分数、冰晶粒径数量密度分布、冰晶平均粒径均有影响。桨叶直径越大,其扰动作用越强,对冰晶的破碎作用越明显,蓄冰槽顶部越不容易形成富冰层。
2) 单螺旋桨桨叶位置对冰晶流动、冰晶体积分数分布影响较大,桨叶距蓄冰槽底部的高度越大,冰晶越不容易在蓄冰槽上部聚集形成富冰层。但桨叶位置对冰晶数量密度分布、冰晶平均粒径影响很小。
3) 双螺旋桨桨叶间距影响蓄冰槽内冰晶分布均匀性,并非桨叶间距越大均匀性越好,而是存在1个最佳值。但桨叶间距对于冰晶平均粒径影响很小。
4) 单、双螺旋桨桨叶直径相同,双螺旋桨能更好地抑制冰晶粒径增长,对冰晶生长的抑制作用更明显。
参考文献:
[1] EGOLF P W, KAUFFELD M. From physical properties of ice slurries to industrial ice slurry applications[J]. International Journal of Refrigeration, 2005, 28(1): 4-12.
[2] KUMANO H, HIRATA T, HAGIWARA Y, et al. Effects of storage on flow and heat transfer characteristics of ice slurry[J]. International Journal of Refrigeration, 2012, 35(1): 122-129.
[3] MICHAEL K, MASAHIRO K. Handbook on ice slurries: fundamentals and engineering[M]. Paris: International Institute of Refrigeration Press, 2005: 11-30.
[4] MIKA L. Ice slurry flow in a poppet-type flow control value[J]. Experimental Thermal and Fluid Science, 2013(45): 128-135.
[5] MASAYUKI T, KOZAWA Y, HIJIKATA K, et al. Prediction of ice storage process in dynamic-type ice storage system[J]. Transactions of the Japan Society of Refrigerating and Air Conditioning Engineers, 2011, 14(1): 87-95.
[6] 青春耀, 肖睿, 宋文吉, 等. 冰浆在蓄冰槽内的蓄冰特性及其均匀度研究[J]. 低温与超导, 2009, 37(5): 41-46.
QING Chunyao, XIAO Rui, SONG Wenji, et al. Study on ice slurry storing characteristics and its uniformity in ice storage tank[J]. Cryogenics & Superconductivity, 2009, 37(5): 41-46.
[7] KANETOSHI H, KASZA K. A method for measuring ice slurry particle agglomeration in storage tanks[J]. Dallas in ASHRAE Transactions, 2000(106): 117-123.
[8] PRONK P, HANSEN T M, INFANTE FERREIRA C A, et al. Time-dependent behavior of different ice slurries during storage[J]. International Journal of Refrigeration, 2005, 28(1): 27-36.
[9] DELAHAYE A, FOURNAISON L, GUILPART J. Characterisation of ice and THF hydrate slurry crystal size distribution by microscopic observation method[J]. International Journal of Refrigeration, 2010, 33(8): 1639-1647.
[10] PRONK P, FERREIRA C A I, WITKAMP G J. Effect of long-term ice slurry storage on crystal size distribution[C]// 5thWorkshop on Ice Slurries of the IIR. Stockholm, Sweden, 2002: 30-31.
[11] HANSEN T M, RADOSEVIC M, KAUFFELD M, et al. Investigation of ice crystal growth and geometrical characteristics in ice slurry[J]. International Journal of HVAC and R Research, 2003, 9(1): 19-32.
[12] 赵腾磊. 冰浆存储过程冰晶动力学演化研究[D]. 长沙: 中南大学能源科学与工程学院, 2013: 21-30.
ZHAO Tenglei. Research on the ice crystal dynamics evolution in ice slurry storage process[D]. Changsha: Central South University. School of Energy Science and Engineering, 2013: 21-30.
[13] XU Aixiang, LIU Zhiqiang, ZHAO Tenglei, et al. Population balance model of ice crystals size distribution during ice slurry storage[J]. International Journal of Air-Conditioning and Refrigeration, 2013, 22(2): 1440001-1-1440001-6.
[14] 赵海波, 郑楚光. 离散系统动力学演变过程的颗粒群平衡模拟[M]. 北京: 科学出版社, 2008: 13-18.
ZHAO Haibo, ZHENG Chuguang. Population balance modeling for the process of the dynamic evolution in dispersed systems[M]. Beijing: Science Press, 2008: 13-18.
[15] JONES G A. Crystallization process systems[M]. London: University College London, 2002: 34-45.
[16] PRONK P. Fluidized bed heat exchangers to prevent fouling in ice slurry systems and industrial crystallizers[D]. Delft: Delft University of Technology, 2006: 22-25.
[17] COULALOGLOU C A, TAVLARIDES L. Description of interaction processes in agitated liquid-liquid dispersions[J]. Chemical Engineering Science, 1977, 32(11): 1289-1297.
(编辑 陈灿华)
收稿日期:2016-06-10;修回日期:2016-08-21
基金项目(Foundation item):国家自然科学基金资助项目(51376198);湖南省自然科学基金资助项目(11JJ22029) (Project(51376198) supported by the National Natural Science Foundation of China; Project(11JJ22029) supported by the Natural Science Foundation of Hunan Province)
通信作者:刘志强,博士,教授,从事储能系统的热动力学研究;E-mail: liuzq@csu.edu.cn