基于遗传蚁群算法的树枝型铁路取送车问题优化

雷友诚^{1, 2}，涂祖耀²，桂卫华¹，吴志飞²，闫福全²

(1．中南大学 信息科学与工程学院，湖南 长沙，410083；

2．湖南大学 电气与信息工程学院，湖南 长沙，410082)

摘要：针对企业铁路货运站的铁路线分布特点和“连送带取”的作业方式，建立树枝型专用线取送车的数学模型，将其归纳为一个典型的旅行商问题。同时提出一种融合遗传算法和蚁群算法特点的遗传蚁群算法(GACA)来解决这种大规模组合优化问题；采用遗传算法生成信息素分布，利用蚁群算法求精确解，有效提高算法的时间效率和求解效率。结合实例计算求得了企业取送车作业问题的最优解。

关键词：遗传蚁群算法；铁路调度；取送车作业；组合优化

中图分类号：U292          文献标志码：A         文章编号：1672-7207(2011)08-2356-07

Optimization of placing-in and taking-out wagons on branch-shaped railway lines based on genetic and ant colony algorithm

LEI You-cheng^{1, 2}, TU Zu-yao², GUI Wei-hua¹, WU Zhi-fei², YAN Fu-quan²

(1. School of Information Science & Engineering, Central South University, Changsha 410083, China;

2. College of Electrical & Information Engineering, Hunan University, Changsha 410082, China)

Abstract: Aiming at the distribution of railway line and a combinatorial mode of placing-in and taking-out wagons at an enterprise railway freight station, a mathematical model of optimal operation for placing-in and taking-out wagons in the branch-shaped private line was established, which is deduced as a typical traveling salesman problem(TSP). Meanwhile, a combination of genetic algorithm and ant colony algorithm called GACA was presented to resolve the large-scale combinatorial optimization problem. The genetic algorithm was adopted to generate pheromone to distribute. And the ant colony algorithm was used to find an accurate solution. As a result, the searching efficiency and the time efficiency of the combinatorial algorithm are both greatly improved. Combined with an example, the optimal solution of the placing-in and taking-out wagons problem is found.

Key words: genetic and ant colony algorithm; railway scheduling; operations for placing-in and taking-out wagons; combinatorial optimization

取送车作业是企业铁路货运站的一项重要工作，对取送车作业的调度安排进行科学优化可以有效压缩车辆在货运站的停留时间，提高企业铁路运输效率，降低企业铁路运营成本。取送车问题按专用线布置形式的不同通常分为放射型(或称为扇形)和树枝型两大类^[1]。本文主要对树枝型专用线取送车问题进行讨论。文献[2]建立了该问题的树形结构模型并提出3个优化目标；文献[3]将其归纳为旅行商问题，提出了一种启发式节约算法；文献[4]将其等同为机器排序问题求解；文献[5]将其抽象为线性矩阵并用模拟退火算法求解；文献[6]运用图论中的汉密尔顿图将其转化为求权值最小的汉密尔顿回路问题；文献[7-8]根据TSP模型分别用遗传算法和蚁群算法求解该问题。这些算法模型成熟可行，但随着装卸作业点的增加，问题求解耗时且难度加大，容易产生组合爆炸。本文作者采用一种遗传算法和蚁群算法融合的遗传蚁群算法(GACA)，针对大型企业自备铁路树枝形专用线的大规模取送车作业问题进行优化研究，并对算法实现和结果进行了  分析。

1  取送车的问题描述

1.1  企业树枝型专用线铁路取送车作业特点

列车在运达铁路货运站完成解体作业后会停在编组站上，等待通过轨道衡检斤并前往各条专用线执行装卸货任务，作业完毕后再原路返回出发轨道集结编组，因而存在取送车作业。树枝形铁路专用线的特点是：在一批作业中间调车机车不用返回编组站，各专用线入线时间不同，但取回时间相同，所以，宜采取连送带取作业方式。某企业铁路货运站树枝型铁路专用线分布如图1所示。图中，V₀代表编组站即调车机车的出发点，V₁~V₆代表各专用线的装卸货场，路段上的数字表示调车机车在专用线各路段的走行时间。

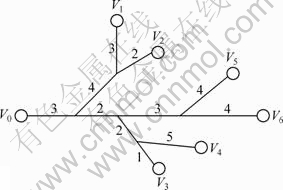
图1  树枝形铁路专用线布置示意图(单位：mm)

Fig.1  Sketch map of branch-shaped railway sidings

1.2  数学模型

在图1中，将机车走行路线上的时间权值加总即得汉密尔顿图中的各边权值，由此得到转化的汉密尔顿图^[6]，如图2所示。

已知编组场只有1台调机，调车机车向各专用线的装卸作业点送车，并且规定仅经过每个作业点1次，最后调机返回编组站。这里只讨论送车顺序，因为送车顺序决定了取车顺序，调车机车送完车回到编组站再沿着已经搜索到的最优路径进行取车作业。由以上分析知本问题变成旅行商问题，即在赋权无向图G中找到调机总走行时间最少的汉密尔顿回路。于是，把问题构造成网络图^[3]，以G=[V，A，C]表示。其中：V={0，1，…，n}表示调机要经过的作业点，V₀为编组站；A={(i，j)|i，j=0，1，…，n，i≠j}表示调机可能走过线路段集合；C={c_ij(i，j)∈A}，c_ij表示调机经过对应弧段(i，j)所需时间，包括调机在(i，j)纯走行时间及在(i，j)作业点进行摘挂、对货位等作业所需时间，通过写实查定，这些时间标准是已知的。设变量：

图2  树枝型专用线的汉密尔顿图

Fig.2  Hamilton graph of branch-shaped railway sidings

以调车机车总行走时间t最小为优化目标，树枝形铁路专用线最优取送顺序问题的数学模型如下。

(1) 目标函数，取送调车作业调机总走行时间t：

           (1)

(2) 约束条件。

           (2)

           (3)

        (4)

2  遗传算法与蚁群算法融合的基本思想

取送车作业优化问题属于典型的NP完全问题，采用经典的数学方法很难求出其精确解。遗传算法(GA)具有快速的全局搜索能力，但同时它对系统中的反馈信息利用不够，而且当求解到一定范围时往往进行多余的冗余迭代，而使得求精确解效率低^[9]。蚁群算法(ACA)具有分布、并行、全局收敛能力，但由于初期信息素匮乏，导致算法速度慢^[10]。

将遗传算法与蚁群算法的优势融合，形成遗传蚁群算法(GACA)来有效解决取送车组合优化问题。融合后的算法其基本思路是：首先利用遗传算法的随机搜索、快速性、全局收敛性等特点，产生有关问题的初始信息素分布；然后，利用蚁群算法的并行性、正反馈机制以及求解效率高等特性求出精确解。这种融合后的遗传蚁群算法比蚁群算法所用时间少、效率高，在求解效率上比遗传算法的高。

3  GACA算法设计

3.1  GACA算法中遗传算法的设计

3.1.1  染色体编码

在进行搜索之前，先将问题解数据表示成遗传空间的基因型串数据结构，每个基因代表1个序列编号。G＝(a₀，a₁，a₂，…，a_n，a₀)表示染色体，代表一个送车方案，其中基因a_i(i=1，2，…，n)为 [1，n]之间的一个互不重复的自然数，它表示第a_i个装卸作业点在调车机车送车路径中的顺序为i。

3.1.2  初始种群生成

为了使取车的等待时间减少，在送车时尽量使装卸量大的作业点排在送车顺序的前面。借用轮盘赌^[11]的思想生成新个体，先计算所有作业点的装卸货量的总和，再计算每个作业点装卸货量在总装卸货量所占的比例，所占比例高的作业点有较大的概率排在送车顺序的前面，由此产生一组取送车方案G_j(j=1，2，…，k)。G_j各不相同，这k个染色体构成第1代种群。

3.1.3  适应度评估

适应度函数采用取送车作业总时间t的倒数，即f=1/t。在算法前期，对一些适应度较高的个体进行控制，降低其适应度，保持种群的多样性，在算法后期对个体的适应度适当放大，提高个体之间的竞争性。

3.1.4  自然选择

采用最优保存的选择策略，将每代种群按个体适应度分为N₁，N₂和N₃部分，适应度最大的N₁个个体直接复制到下一代群体，N₂个中间个体进行交叉变异，适应度最小的N₃个个体直接淘汰，并在一定概率上按启发式知识产生N₃个新个体以保持种群的    规模。

3.1.5  交叉重组

在选择操作之后，根据选择概率P_c选择个体进行交叉重组。交叉规则采用PMX法^[12]，处理方法如下：设父代的2个染色体为G_a=(0 8 4 5 6 7 1 3 2 0)，G_b=(0 7 8 1 2 3 5 4 6 0)。随机选择交配区域如下：G_a=(0 8 4 5|6 7 1|3 2 0)→G_a'=(0 8 4 1|2 3 5|7 6 0)，G_b =(0 7 8 1|2 3 5|4 6 0)→G_b'=(0 3 8 5|6 7 1|4 2 0)。

从上述变换可知：PMX交叉算子能够有效地继承双亲的部分基因成分，实现了进化过程中的遗传    功能。

3.1.6  变异算子

根据变异概率P_M对染色体进行变异操作，取送车问题要求在同一路径中不能有重复的作业点(开始结点和终止结点除外)。一般的变异算子可能会导致非法路径产生，为了不引入非法路径，本文选用逆转变异^[13]的优化策略。

3.2  GACA算法中遗传算法与蚁群算法的衔接

通过遗传算法可以得到若干组优化送车路径，这些路径决定了蚁群算法的初始信息素分布，在初始t₀时刻，作业点(i，j)间的信息素生成规则如下：

        (5)

其中，G_better为遗传算法中得到若干组较优送车路径；τ_C为根据取送车作业优化问题规模(如装卸作业点数量)给定的一个信息素常数；τ_G为遗传算法求解出的若干组优化解转换的信息素值。

3.3  GACA算法中蚁群算法的设计

在GACA算法中，蚁群算法采用最大-最小蚂蚁系统^[14]，该系统有以下2个特点：

(1) 充分利用循环最优解和到目前为止找出的最优的解，在每次循环之后，只有1只蚂蚁进行信息素更新。这只蚂蚁可能是找出当前循环中最优解的蚂蚁(迭代最优的蚂蚁，Iteration-best ant)，也可能是找出从实验开始以来最优解的蚂蚁(Global-best ant)。

(2) 为避免搜索的停滞，在每个解的元素(在TSP中是每条边)上的信息素轨迹量的值域范围被限制在区域[τ_min，τ_max]内。

这种算法在防止算法过早停滞以及有效性方面较蚁群系统^[15-18](Ant colony system, ACS)算法有较大的  改进。

在蚁群算法中，每个蚂蚁根据状态转移规则来选择下一作业点。在路径建立过程中，蚂蚁通过应用局部更新来修改已访问路径上的信息素量。一旦蚂蚁都完成了它们的路径，应用全局更新规则再次对路径上的信息素量进行修改。信息素值全局更新和局部更新规则如下。

3.3.1  状态转移规则

在t时刻，位于作业点i的第k只蚂蚁选择下一作业点j的规则及在作业点i和j间的转移概率  如下：

  (6)

       (7)

上述规则被称为伪随机比例规则。其中，q为在[0，1]区间均匀分布的随机数；q₀为参数(0≤q₀≤1)，若q≤q₀，则按先验知识选择路径。τ_ij(t)表示2个作业点i和j间的信息素值，α(α＞0)表示路径轨迹的相对重要性，β(β＞0)表示路径能见度的相对重要性，allowed_k={0，1，…，n}表示蚂蚁k下一步可以选择的作业点集；η_ij=1/d_ij表示边(i，j)的能见度，d_ij表示机车在作业点i和j间的走行时间。

3.3.2  信息素的全局更新规则

在蚁群系统中，只有全局最优的蚂蚁才被允许释放信息素，全局更新在所有蚂蚁都完成它们的1次路径搜索之后执行，更新公式如下：

      (8)

表示在t时刻作业点i,j间信息素的增加量：

    (9)

其中：ρ(0＜ρ＜1)表示信息素挥发参数；L_best为到目前为止找出的全局最优路径。由式(9)可知：只有那些属于全局最优路径的边上的信息素才会得到增强。

3.3.3  信息素的局部更新规则

在搜索路径的同时，每只蚂蚁应用局部更新规则对它们经过的边进行激素更新，更新公式如下：

     (10)

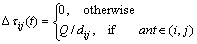     (11)

其中：Q为蚂蚁在经过路径(i，j)上释放的每单位长度的信息素量，若蚂蚁经过路径(i，j) ，则进行信息素的更新。

综上所述，用遗传蚁群算法解决取送车调车作业优化问题的流程如图3所示。

图3  遗传蚁群算法的实现流程

Fig.3  Procedure graph of GACA

4  实例计算与结果分析

已知某企业铁路编组场(编号0)连接专用线14条(编号1~14)。该货运站仅有1台调车机车担当取送作业，现有14列车组要送往各专用线进行装卸作业，已知机车在编组站各作业点之间的走行时间C_ij(见    表1)。

分别运用标准蚁群算法(ACA)和遗传蚁群算法(GACA)对上例问题进行仿真，各自独立运行20次。用15个互不重复的0~14的自然数构建1个染色体，表示1种送车方案。GACA算法的参数设置包括：限定总迭代次数N_Cmax=200为结束条件，遗传算法迭代次数为80(固定)，群体规模N=50，P_C=95%，P_M=5%。蚁群算法中各路径信息素初值τ_C设为60，τ_G=2，转移概率公式中α=1，β=5。轨迹更新公式中ρ=0.7，Q=     1 000。ACA算法中的参数设置同GACA算法中的蚁群部分。运用MATLAB语言上机求解，GACA得到最优的送车顺序为0—2—1—3—7—9—8—14—12—13—6—11—4—5—10—0,送车消耗总行走时分为1.035×10⁴ s≈173 min。最优解优化逼近过程的对比仿真结果如图4所示。记录在GACA算法每个阶段的优化解分布如表2所示。

从图4和表2可知：蚁群算法(ACA)由于初期信息素不足，求解速度慢，搜索过早停滞；而GACA算法在经历了80代的遗传算法快速全局搜索之后，蚁群算法再利用遗传算法遗留的路径信息素进行分布式搜索，找到了更满意的解。GACA算法由于在遗传算法中使用基于知识的初始种群，不仅加快了蚁群算法的速度，而且以一定的概率收敛于最优解；遗传算法与蚁群算法的融合对蚁群算法中的参数调整大大减低，大大减少了盲目实验的次数。

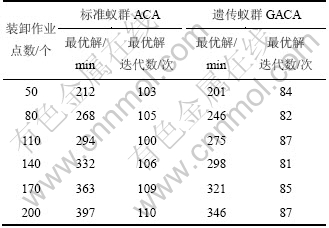
为验证GACA算法在大规模取送车作业问题上应用的可行性，分别运用标准蚁群算法(ACA)和遗传蚁群算法(GACA)对装卸点大规模增加的情况进行仿真，对比结果如表3所示。

由表3可以看出：随着装卸作业点个数的增加，GACA的寻优性能明显优于ACA，不仅收敛速度更快，而且找到的最优解也更令人满意。

表1  编组场与各作业点间的行走时间

Table 1  Travel time between marshalling yard and operating points                     min

表2  GACA算法优化解数据的逼近过程

Table 2  Process of optimal data approximation of GACA algorithm                   min

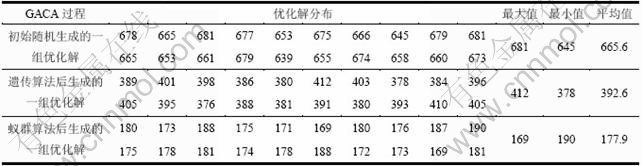
图4  GACA和ACA的最优解演化对比结果

Fig.4  Comparison of optimal solution between GACA and ACA

表3  算法规模扩大时GACA和ACA的对比仿真结果

Table 3  Comparison of simulation results between GACA and ACA when scale of algorithm increases

5  结论

(1) 经过遗传算法的初步搜索并生成初始信息素分布，增强了蚁群算法的正反馈机制，使得蚁群算法中的参数调整程度大大降低。

(2) 遗传算法与蚁群算法结合后，在算法的收敛速度加快的同时，蚁群算法中的参数α，β和ρ对取送车问题规模变化的敏感度降低，提高了算法的鲁    棒性。

(3) 在蚁群算法阶段使用最大-最小蚂蚁系统(MMAS)，而且同时采用信息素的局部更新和全局更新规则，使得算法在一定程度上避免陷入局部最优。

参考文献：

[1] 彭其渊, 王慈光.铁路行车组织[M].北京: 中国铁道出版社, 2007: 62-63.
PENG Qi-yuan, WANG Ci-guang. Train operation organization[M]. Beijing: China Railway Publishing House, 2007: 62-63.

[2] 王慈光. 树枝型专用线取送车问题的研究[J]. 西南交通大学学报, 1996, 31(6): 675-680.
WANG Ci-guang. A study on placing-in and taking-out of wagons on brached-shaped sidings[J]. Journal of Southwest Jiaotong University, 1996, 31(6): 675-680.

[3] 余少鹤, 李夏苗. 货物作业车取送车模型及算法研究[J]. 铁道运输与经济, 2002, 24(12): 46-48.
YU Shao-he, LI Xia-miao. The model of placing-in and taking-out for working wagons and the calculation methods[J]. Railway Transport and Economy, 2002, 24(12): 46-48.

[4] 敬媛媛. 树枝型专用线取送车算法的研究[J]. 成都大学学报: 自然科学版, 1998, 17(4): 36-42.
JING Yuan-yuan. A study on the sequence of placing-in and taking-out wagons of branch-shaped siding line[J]. Journal of Chengdu University: Natural Science Edition, 1998, 17(4): 36-42.

[5] 潘灵巧, 林志安. 关于树枝型专用线取送车问题的探讨[J]. 内蒙古科技与经济, 2008(6): 288-289.
PAN Ling-qiao, LIN Zhi-an. The discussion of the sequence of placing-in and taking-out wagons of branch-shaped siding line[J]. Inner Mongolia Science Technology & Economy, 2008(6): 288-289.

[6] 石红国, 彭其渊, 郭寒英. 树枝型专用线取送车问题的哈密尔顿图解法[J]. 中国铁道科学, 2005, 26(2): 132-135.
SHI Hong-guo, PENG Qi-yuan, GUO Han-yin. An algorithm by using hamilton graph to resolve wagons’ placing-in and taking out on branch-shaped sidings[J]. China Railway Science, 2005, 26(2): 132-135.

[7] 杨云贵, 王慈光, 薛峰. 树枝型专用线取送车问题的遗传算法研究[J]. 计算机工程与应用, 2008, 44(12): 210-211.
YANG Yun-gui, WANG Ci-guang. Study on genetic algorithm for railway placing-in and taking-out wagons in branch-shaped private silding[J]. Computer Engineering and Applications, 2008, 44(12): 210-211.

[8] 李智. 基于改进型蚁群算法的货物作业车取送模型优化[J]. 铁道运输与经济, 2004, 26(4): 73-76.
LI Zhi. Optimization of Placing-in and taking-out wagon operation model based on enhanced ant colony algorithm[J]. Railway Transport and Economy, 2004, 26(4): 73-76.

[9] 李敏强, 徐博艺, 寇纪松. 遗传算法与神经网络的结合[J]. 系统工程与实践, 1999, 19(2): 65-69.
LI Ming-qiang, XU Bo-yi, KOU Ji-song. On the combination of genetic algorithms and neural networks[J]. Systems Engineering Theory & Practice, 1999, 19(2): 65-69.

[10] 吴庆洪, 张纪会, 徐心和. 具有变异特征的蚁群算法[J]. 计算机研究与发展, 1999, 36(10): 1240-1245.
WU Qing-hong, ZHANG Ji-hui, XU Xin-he. An ant colony algorithm with mutation features[J]. Journal of Computer Research and Development, 1999, 36(10): 1240-1245.

[11] 陈有青, 徐蔡星, 钟文亮, 等. 一种改进选择算子的遗传算法[J]. 计算机工程与应用, 2008, 44(2): 44-49.
CHEN You-qing, XU Cai-xing, ZHONG Wen-liang, et al. Genetic algorithm with improved selection operator[J]. Computer Engineering and Applications, 2008, 44(2): 44-49

[12] Goldberg D E, Jr Lingle R. Alleles, loci and the traveling salesman problem[C]//Second Int Conf on Genetic Algorithms and Their Applications Pittsburgh, 1985: 154-159.

[13] 余伶俐, 蔡自兴. 改进混合离散粒子群的多种优化策略算法[J].中南大学学报: 自然科学版, 2009, 40(4): 1047-1053.
YU Ling-li, CAI Zi-xing. Multiple optimization strategies for improving hybrid discrete particle swarm[J]. Journal of Central South University: Science and Technology, 2009, 40(4): 1047-1053.

[14] Stutzle T, Hoos H H. MAX-MIN ant system[J]. Future Generation Computer System, 2000, 16(8): 889-914.

[15] Dorigo M, Gambardella Luca Maria. Ant colony: a cooperative learning approach to the traveling salesman problem[J]. IEEE Trans on Evolutionary, 1997, 1(1): 53-66.

[16] Chang P C, Huang W H, Ting C J. Dynamic diversity control in genetic algorithm for mining unsearched solution space in TSP problems[J]. Expert Systems with Applications, 2010, 37: 1863-1878.

[17] Lee Z J, Su S F, Chuang C C, et al. Genetic algorithm with ant colony optimization (GA-ACO) for multiple sequence alignment[J]. Applied Soft Computing, 2008, 8: 55-78.

[18] Chen S M, Chien C Y. Parallelized genetic ant colony systems for solving the traveling salesman problem[J]. Expert Systems with Applications, 2011, 38: 3873-3883.

(编辑 赵俊)

收稿日期：2011-01-17；修回日期：2011-04-07

基金项目：湖南省自然科学基金资助项目(11JJ3068)；长沙市科技计划项目(K0802079-11)

通信作者：雷友诚(1964-)，男，湖南邵阳人，副研究员，博士研究生，主要从事智能控制与优化研究；电话：13055161017；E-mail：jt_lyc@hnu.cn