高围压高孔隙水压作用下岩石蠕变特性
刘东燕1,蒋海飞1,李东升1,赵宝云2
(1. 重庆大学 土木工程学院,重庆,400045;
2. 重庆科技学院 建筑工程学院,重庆,401331)
摘要:对重庆某地深部砂岩进行高围压和高孔隙水压作用下分级加载蠕变试验。结果表明:加载初期的一较短时间内,孔隙水压力在一定程度上延缓轴向变形,随后整个加载过程表现为增强岩石轴向变形。相同围压下,有孔隙水压和无孔隙水压时岩石蠕变可能存在一个相同的应力强度比阀值,当应力强度比超过该阀值后便会出现加速蠕变破坏。选取三元件广义Kelvin模型描述高围压高孔隙水压作用下加载应力低于屈服应力σs时的岩石蠕变特性,效果较为理想。基于高围压高孔隙水压作用下砂岩加速蠕变试验曲线特性,采用拟合、类比的方法引入一个二元件黏塑性模型,将其与三元件广义Kelvin模型串联组成一个新的可以描述岩石加速蠕变全过程的非线性黏弹塑性蠕变模型。采用基于Quasi-Newton非线性优化算法(BFGS)的Matlab编程,实现对高围压高孔隙水作用下岩石加速蠕变全过程曲线进行辨识,对比试验曲线和模型拟合曲线,二者吻合较好,验证非线性黏弹塑性模型的正确性。
关键词:高围压;高水压;砂岩;蠕变;非线性蠕变模型
中图分类号:TU458 文献标志码:A 文章编号:1672-7207(2014)06-1916-08
Creep properties of rock under high confining pressure and high water pore pressure
LIU Dongyan1, JIANG Haifei1, LI Dongsheng1, ZHAO Baoyun2
(1. College of Civil Engineering, Chongqing University, Chongqing 400045, China;
2. School of Civil Engineering and Architecture, Chongqing University of Science and Technology,
Chongqing 401331, China)
Abstract: Step loading triaxial creep test was carried out for deep sandstone from somewhere in Chongqing under high confining pressure and high pore water pressure. The result shows that the pore water pressure delays the rock creep deformation to some extent at the initial stage, but then to enhance performance of rock creep deformation; with or without pore water pressure, there might be a definite threshold of stress strength ratio under which the tertiary stage of creeps in different loading conditions begin to occur. The three component modified Kelvin model is selected to describe the characteristics of rock creep when the loading stress is below the yield stress. Based on the action of sandstone accelerating creep curves under the loading condition of high confining pressure and high pore water pressure, a two-component viscoplastic model is acquired by the method of fitting and anology, which is connected with three- component modified Kelvin model in series, and then a new nonlinear viscoelastic-plastic constitutive model is obtained. The Matlab programming based on Quast-Newton nonlinear optimization algorithm (BFGS) is adopted to identify the model parameters. Comparing testing curves with fitting curves, it is shown that this new model is suitable to describe the three creep stages of rocks.
Key words: high confining pressure; high pore water pressure; sandstone; creep; nonlinear creep model
蠕变特性是岩石的一个重要力学性质,与工程的长期稳定和安全密切相关。大量工程实践表明,岩石蠕变是工程产生大变形乃至失稳的重要原因之一[1]。近年来随着基础工程建设中深长隧道不断涌现,如秦岭隧道、锦屏引水隧道、青藏铁路新关角隧道等,高地应力与高孔隙水压力作用下隧道围岩开挖变形稳定性问题日益突出。因此加强对高应力高孔隙水压力作用下岩石蠕变特性的研究,提出一种适用的蠕变模型,不仅可以加强对复杂环境下岩体流变规律的进一步认识,还能为岩土工程的设计、施工和运行提供更全面、更可靠的基础资料。目前国内外对岩石蠕变模型方面的研究已经取得很多成果。使用较多的有Kelvin模型、Burgers模型和西原模型等。然而元件理论所用的基本元件都是线性的,无论构成模型的元件怎么多、组合方式多么复杂,最终得到的本构关系还是线性的,不能研究非线性蠕变[2],也就无法描述岩石加速蠕变阶段。因此需要对其改进以建立非线性蠕变模型。目前,建立岩石非线性蠕变模型的方法主要有以下2种:一是通过对常规线性蠕变模型中的蠕变参数建立与时间的非线性关系,以获得对加速蠕变阶段的描述;二是提出新型蠕变模型,建立对应的本构关系,并将其与传统模型串联组成新的非线性黏弹塑性蠕变模型。国内具有代表性的岩石非线性蠕变模型有徐卫亚等[3]通过将岩石非线性黏塑性体与五元件黏弹性模型串联,建立了岩石七元件非线性黏弹塑性蠕变模型;王来贵等[4]提出采用非线性牛顿体模型来取代稳定蠕变过程中的线性牛顿体模型,得到了能够描述岩石加速蠕变状态的理论模型;曹树刚等[5]通过将黏滞体模型中的黏滞系数修正为非线性,提出了一种组合模型,能较好的反应岩石的加速蠕变特性。陈沅江等[6]提出了适用于软岩的裂隙塑性体模型和用于描述岩石加速蠕变的蠕变体模型,并对裂隙性体和蠕变体的本构关系进行了定量描述。夏才初等[7-8]提出了同时包含黏弹性、黏塑性、黏性、黏弹塑性4种基本流变力学性态的流变模型,并对模型的参数识别进行了研究。袁海平等[9]基于Mohr-Coulomb准则提出改进的Burgers蠕变模型。以上这些研究均对岩石蠕变过程给出了定量的描述,并通过试验加以验证,取得了较为丰硕的成果,但总体来说,目前这方面的研究仍有待于进一步丰富和完善。特别是在深部岩体开挖过程中,水的作用使得围岩的结构和力学性能恶化,实际载荷高于表观载荷使得由高地应力引起的岩体的蠕变变形大大增加,给工程带来了极大的安全隐患。目前对于高围压高孔隙水压作用下的岩石蠕变特性研究较少,对于高围压高孔隙水压作用下的岩石蠕变模型更是鲜见报道。
基于此,本文作者选取重庆地区某深基坑砂岩为研究对象,对其进行高围压以及高围压高孔隙水压作用下三轴压缩蠕变试验,在对试验结果分析的基础上,采用三元件广义Kelvin模型描述高围压高孔隙水压作用下,加载应力低于屈服应力时的黏弹性蠕变特性;并基于高围压高孔隙水压作用下砂岩的加速蠕变试验曲线特性,采用拟合、类比的方法推导了二元件黏塑性模型的非线性本构关系,将得到的二元件非线性黏塑性模型与三元件广义Kelvin模型串联组成一个新的非线性黏弹塑性蠕变模型。采用基于Quasi-Newton非线性优化算法(BFGS)的Matlab编程,实现对高围压高孔隙水压作用下岩石加速蠕变全过程试验曲线进行辨识。研究结果可为高应力高水压地区深部岩体的开挖提供一定的理论指导。
1 三轴压缩蠕变试验与成果分析
1.1 试验设备
本次试验采用RLW-2000岩石三轴流变试验系统,如图1所示。该系统由轴向加载系统、围压加载系统、孔压加载系统、伺服系统、控制系统、数据采集和自动绘图系统等部分组成。轴向加载系统和围压加载系统的控制部分采用全数字伺服控制器(EDC)。

图1 试验装置
Fig. 1 Test device
1.2 试验设计
本次蠕变试验设计了2种加载方式,三轴蠕变试验工况见表1。岩样按照国际岩石力学会(ISRM)试验规程,制备成直径50 mm、高度100 mm的圆柱体。
试验中,1号试件不受孔隙水压力作用,看作参照试件。若2号试件蠕变试验结果与1号试件蠕变试验结果相近,则说明2号试件几乎不受孔隙水压力的影响;若两者差异很大则说明孔隙水压力对岩石蠕变有影响[10]。
在试验之前分别对2种工况下岩石进行了常规三轴压缩试验,得到3种工况下岩石的峰值破坏强度σmax、屈服强度σs、轴向极限应变εmax,表2所示为砂岩三轴压缩试验结果。
表1 三轴蠕变试验工况
Table 1 Work conditions of triaxial creep test

表2 砂岩三轴压缩试验结果
Table 2 Test result of sandstone under triaxial compression

1.3 试验过程
在试验开始之前对2号试件进行了饱水处理:先用真空饱水机饱水24 h,再放入水中浸泡7 d。试验过程如下:
(1) 首先用热缩管套住岩石试件,并用电吹风使热缩管与试件紧密接触;
(2) 将用于施加水压的进出水管安装在试件上;
(3) 将试件置于三轴室圆形底座上,安装好径向和轴向引伸计,封闭三轴室腔体。
(4) 待所有准备工作就绪后,向三轴室内充油,充油完毕,通过电脑控制系统输入试验所需围压、轴压和孔隙水压力。
(5) 在进行有孔隙水压的岩石蠕变试验中,先施加围压,待围压达到设定值后,再施加孔隙水压。当围压和孔隙水压力都达到预设值时,保持当前加载状态,直到出水口有少许水珠滴出。这是为了保证整个岩石试件内部均充满孔隙水压力。
(6) 完成上述步骤后,开始分级施加轴向荷载进行蠕变试验。
1.4 蠕变特征分析
由试验获得的不同加载条件下轴向蠕变试验曲线见图2。由图2可见:2种加载条件下,蠕变增量随着应力水平的增加而增加,而且每一级轴向蠕变量与每一级瞬时弹性变形量之比也同样在增加,即随着应力水平的提高,蠕变量在总变形中所占的比例增加。加载初期两蠕变曲线比较接近,但随着试验的进行,二者逐渐偏离。

图2 不同加载条件下砂岩分级加载蠕变曲线
Fig. 2 Creep strains under different loading conditions
在第一级应力水平加载初期的一段时间内(约8 h),有孔隙水压作用的2号试件蠕变曲线位于相同围压下无孔隙水压作用的1号试件蠕变曲线下方。
变试验加载初期,应力水平较低,岩石内部孔隙大都处于相互隔绝状态或是通过极微小的裂隙连接,且受到高围压的限制,孔隙水排出极为缓慢,孔隙水会在裂纹面上产生一个反向的抵抗作用,延缓轴向变形,即短时间内含孔隙水压力的试件变形模量有所提高。文献[11]也得到相似结论。这就解释了图2中2号试件蠕变曲线在第一级应力水平作用初期,位于1号试件蠕变曲线下方的现象。
另一方面,孔隙水压也会在孔隙的裂纹尖端形成一个附加的拉力,增强裂纹的扩展能力,随着裂纹的不断扩展,原生孔隙间不断连通,连接孔隙的裂纹在应力作用下也不断增大,水被挤压排出孔隙的速度加快,孔隙水压抵抗轴向变形的能力将逐渐减弱直至消失,此后,岩石强度不断劣化,岩石中孔隙水转而起到促进岩石变形的作用。宏观表现为2号试件蠕变曲线从第一级应力水平加载后期逐渐超越并偏离1号试件蠕变曲线,且偏离程度越来越大。
1号试件在应力强度比达到0.812 5时,出现了加速蠕变阶段。2号试件在应力强度比达到0.807 6时,在经历短暂的衰减蠕变和稳态蠕变后也出现了加速蠕变。2种情况下出现加速蠕变阶段的应力强度比非常接近,据此推断,相同围压下,有孔水压力和无孔隙水压2种条件下,岩石蠕变可能存在一个相同的应力强度比阀值,当应力强度比超过该阀值后便会出现加速蠕变破坏。
2 三元件广义Kelvin模型
由于采用了分级加载方式,因此需利用Boltzmann叠加原理,将分级加载条件下的蠕变曲线转化为分别加载条件下的蠕变曲线,转化后得到的高围压高孔隙水压作用下砂岩蠕变曲线如图3所示。

图3 高围压高孔隙水压作用下砂岩三轴压缩蠕变试验曲线与理论曲线对比
Fig. 3 Comparison between theoretical curves and triaxial compression creep curves under high confining pressure and high pore water pressure
由试验结果可知:当加载偏应力低于屈服应力水平时,蠕变具有明显的黏弹性特征。元件模型中的Kelvin模型和Burgers模型弹性体都可以较好的描述具有衰减蠕变和稳定蠕变特征的蠕变曲线,并且模型简单实用[12]。由于三元件广义Kelvin模型参数相对较少,便于参数的识别,故本文采用三元件广义Kelvin模型描述砂岩在应力低于屈服强度时的蠕变特性。一维条件下,三元件广义Kelvin蠕变模型的公式为:
 (1)
(1)
岩石在三维应力状态下,其内部的应力张量可分解为球应力张量σm和偏应力张量Sij,其表达式分别如下:
 (2)
(2)
式中:δij为Kronecker函数,由式(2)可得:
 (3)
(3)
通常认为,球应力张量σm只能改变物体体积;而偏应力张量Sij只引起形状变化。因此也可以将应变张量分解成球应变张量εm和偏应变张量eij,表达式如下:
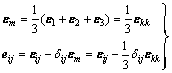 (4)
(4)
由式(4)可得:
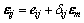 (5)
(5)
对应三维应力状态下的虎克体有:
 (6)
(6)
式中:K为体积模量,G为剪切模量。假定岩石各向同性,弹性应变由应力球张量引起,蠕应变主要由应力偏张量引起。结合前面各式可得三维应力状态下三元件广义Kelvin蠕变模型公式:
 (7)
(7)
据此可以得到等围压三轴压缩时岩石在恒定应力条件下的蠕变方程:
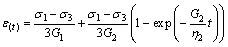 (8)
(8)
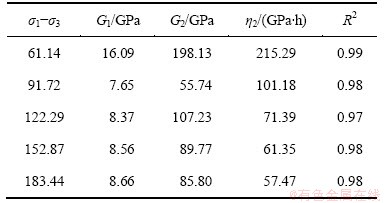
采用Origin8.0数据分析软件对蠕变力学参数进行辨识,辨识结果见表3,对应的拟合曲线见图3。拟合相关性系数的平方R2均在0.97以上,拟合效果较好,说明三元件广义Kelvin蠕变模型可以表征高围压高水压条件下是砂岩的黏弹性三轴压缩蠕变特性。
表3 三元件广义Kelvin蠕变模型参数
Table 3 Parameters identification of modified three-Component Kelvin creep model
3 非线性黏弹塑性蠕变模型
3.1 非线性黏塑性模型
三元件广义Kelvin模型无法描述加速蠕变阶段的变化规律,而加速蠕变是岩石破坏的关键环节,因此有必要对高围压高孔隙水压作用下加速蠕变阶段蠕变模型作进一步研究。
加速蠕变阶段,应变与时间呈非线性关系,元件模型中,用来表示应变-时间关系的为黏性元件,因此可以用非线性黏性元件代替模型中线性黏性元件[13]。基于此,本文通过拟合、类比的方法提出一个非线性黏性元件,采用应力触发方式,将其与塑性元件并联,组成一个新的非线性黏塑性元件。
采用指数函数对高围压高孔隙水压作用下砂岩三轴压缩加速蠕变曲线进行拟合,其表达式为
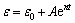 (9)
(9)
式中:ε0为加速蠕变之前的应变;A为拟合参数,代表应力历时参数;t为蠕变时间;n为加速蠕变参数。
图4所示为应用式(9)得到的高围压高孔隙水压作用下砂岩三轴压缩蠕变试验加速蠕变段曲线与理论曲线的对比,对应的拟合参数ε0,A和n分别为0.007 4,8.661 5×10-5和0.371 8;曲线拟合相关系数平方R2为0.999 7。
从拟合结果可以看出:采用指数函数对高围压高孔隙水压作用下砂岩三轴压缩蠕变的加速蠕变曲线进行拟合,其拟合线型吻合效果很好。

图4 加速蠕变曲线与理论曲线对比
Fig. 4 Comparison between theoretical curve and accelerate creep curve
对于二元件黏塑性蠕变模型,当σ>σs时,其蠕变方程可表示为:
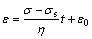 (10)
(10)
对比式(9)与(10),令两式相等,并取 ,则可以得到黏性元件η的非线性表达式:
,则可以得到黏性元件η的非线性表达式:
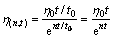 (11)
(11)
式中:t0为参考时间,这里设为1;η0为加速蠕变初始黏性系数;n为加速蠕变指数。
经过处理后得到的非线性黏塑性模型如图5所示。该模型可以充分反映岩石在不同应力状态下的加速蠕变特征,其相应的蠕变本构方程可表示为:
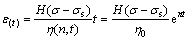 (12)
(12)
式中:σs为岩石的屈服强度;函数H(σ-σs)的表达式如下:
 (13)
(13)
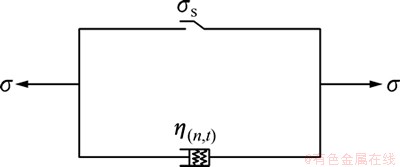
图5 非线性黏塑性模型
Fig. 5 Nonlinear visco-plastic model
3.2 非线性黏弹塑性模型
将上述非线性黏塑性模型与三元件广义Kelvin蠕变模型串联起来,构建一个新的五元件非线性黏弹塑性蠕变模型,如图6所示。该模型也可以看作一种改进的西原模型。

图6 五元件非线性黏弹塑性蠕变本构模型
Fig. 6 Five-component nonlinear viscoelasto-Plastic creep constitutive model
一维条件下,当σ≤σs时,非线性黏滞系数牛顿体不起作用,仅有1,2部分参与蠕变,此时蠕变模型为三元件广义Kelvin模型。
当σ>σs时,1,2和3部分均参与蠕变,此时蠕变模型为五元件非线性黏弹塑性模型,其相应状态方程如下:
 (14)
(14)
整理上式得相应本构方程为:

 (15)
(15)
式中:σ与ε分别为模型的总应力与总应变;σ1,σ2和σ3分别为图6中1,2和3对应部分的应力;ε1,ε2和ε3分别为1,2和3对应部分的应变;E1和E2为岩石材料的弹性参数;η2和η0为岩石黏性参数,其中η0为图6中η(n,t)的初值。
在常应力作用下,假设σ=σ0,将σ=σ0代入式(15),对上述本构方程求解,采用Laplace变化及其逆变换,可以得到五元件非线性黏弹塑性模型一维情况下的蠕变方程:
 (16)
(16)
结合等围压三维应力状态下,三元件广义Kelvin模型公式,得到非线性黏弹塑性蠕变模型公式如下:

 (17)
(17)
3.3 非线性黏弹塑性模型的蠕变特性
对式(17)两边同时对时间进行一次和二次求导,可得:
 (18)
(18)

 (19)
(19)
从式(18)和(19)可以得出:当n=0时,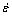 >0,
>0, <0,这时蠕变模型只能反映岩石蠕变全过程曲线中的衰减蠕变和稳态蠕变,而不能反映岩石的加速蠕变;而当n>0时,
<0,这时蠕变模型只能反映岩石蠕变全过程曲线中的衰减蠕变和稳态蠕变,而不能反映岩石的加速蠕变;而当n>0时,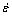 恒大于0,
恒大于0, 可以小于0、等于0或大于0,因此能够描述岩石蠕变全过程曲线的衰减蠕变、稳态蠕变和加速蠕变;此外,n反映了加速蠕变速率,n越大,表示加速蠕变速率越大。
可以小于0、等于0或大于0,因此能够描述岩石蠕变全过程曲线的衰减蠕变、稳态蠕变和加速蠕变;此外,n反映了加速蠕变速率,n越大,表示加速蠕变速率越大。
3.4 模型参数识别及验证
采用好的拟合技术,提高拟合精度,使拟合曲线更好的与试验资料相吻合,对正确选择蠕变模型及确定相应的参数是至关重要的[14]。最小二乘法在岩石蠕变模型参数估计法中一直被广为使用。但是,该方法对于解决非线性问题,效果不甚理想。目前,不少学者对非线性蠕变模型中的加速蠕变阶段采取单独拟合的方法[15-16],通过这样处理虽取得了较好的拟合效果,但破坏了岩石非线性蠕变模型的整体性。因此,本文作者采用基于Quasi-Newton非线性优化算法(BFGS)的Matlab编程,实现对高围压高孔隙水作用下岩石加速蠕变全过程曲线的辨识,辨识得到的五元件非线性黏弹塑性模型参数如表4所示。从表4可以看出:参数拟合相关系数平方R2为0.99,拟合效果相当理想,验证了本文提出的蠕变模型的正确性和适用性。
表4 非线性蠕变模型参数
Table 4 Parameter identification of nonlinear creep model
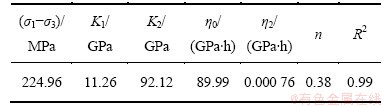
图7所示为高围压高孔隙水压作用下蠕变的模型拟合曲线与试验曲线对比。从图7可以看出:模型拟合曲线与试验曲线吻合效果较好。模型拟合曲线既反映了第1阶段的衰减蠕变特性与第2阶段的稳定蠕变特性,又反映了第3阶段的加速蠕变特性。由此可见,本文提出的五元件非线性黏弹塑性模型可以准确描述高围压高孔隙水压作用下砂岩在高于屈服应力水平下的蠕变力学特性。
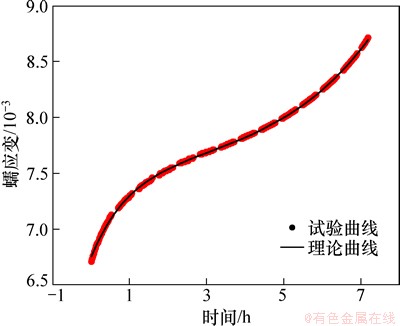
图7 非线性蠕变试验曲线与理论曲线对比
Fig. 7 Comparison between nonlinear creep test curve and theoretical curve
4 结论
(1) 高围压高孔隙水压作用下,由于高围压对孔隙水的限制、岩石原生孔隙和裂隙等缺陷相对分散隔绝,以及岩石本身渗透率很低,导致孔隙水的排除极其缓慢,加载初期,在一定程度上会延缓蠕变变形;但随着裂纹的不断扩展,原生孔隙间不断连通,孔隙水加速排除,孔隙水压力延缓变形的能力将逐渐减弱直至消失,转而起到促进岩石变形的作用。
(2) 高围压条件下,无论有无孔隙水压力,可能存在统一的应力强度比阀值,当应力强度比超过该阀值后,便会产生加速蠕变破坏。
(3) 推导了常规三轴应力状态下的三元件广义Kelvin模型,并用该模型对高围压高孔隙水压作用下,加载偏应力低于屈服应力时砂岩的线性黏弹性蠕变特性进行描述,对比模型拟合曲线与试验曲线,二者吻合较好。
(4) 采用指数函数对高围压高孔隙水压作用下砂岩加速蠕变曲线进行拟合,并通过类比的方法引入非线性黏塑性元件,将其与三元件广义Kelvin模型串联起来,构建一个新的非线性黏弹塑性蠕变模型。该模型可以表述岩石在不同应力水平作用时的衰减蠕变、稳定蠕变和加速蠕变。
(5) 根据高围压高孔隙水压作用下砂岩三轴压缩全过程蠕变试验数据,采用基于Quasi-Newton非线性优化算法(BFGS)的Matlab编程,对所提出的非线性黏弹塑性蠕变模型进行了辨识,辨识结果和试验结果吻合较好。验证了本文中提出的蠕变模型的正确性和适用性。
(6) 本次试验过程中,横向传感器出现故障,导致本次试验未能监测到试样的横向应变,也就没有考虑本文提出的模型对横向蠕变的适用性,作者将在后续研究中对其完善。此外,本文试验所用岩样取自重庆地区某深基坑,由于不同岩石蠕变性质千差万别,因此,提出的蠕变本构模型是否适用于其他种类岩石还有待进一步研究和探讨。
参考文献:
[1] 蔡美峰, 何满潮, 刘东燕. 岩石力学与工程[M]. 北京: 科学出版社, 2009: 8-9.
CAI Meifeng, HE Manchao, LIU Dongyan. Rock mechanics and engineering[M]. Beijing: Science Press, 2009: 8-9.
[2] 孙钧. 岩土材料流变及其工程应用[M]. 北京: 中国建筑工业出版社, 1999: 26-31.
SUN Jun. Rheological behavior of geomaterials and its engineering applications[M]. Beijing: China Archtecture and Building Press, 1999: 26-31.
[3] 徐卫亚, 杨圣奇, 谢守益, 等. 绿片岩三轴流变力学特性的研究(Ⅱ):模型分析[J]. 岩土力学, 2005, 26(5): 693-698.
XU Weiya, YANG Shengqi, XIE Shouyi, et al. Investigation on triaxial rheological Mechanical properties of green schist specimen(Ⅱ): Model analysis[J]. Rock and Soil Mechanics, 2005, 26(5): 693-698.
[4] 王来贵, 何峰, 刘向峰, 等. 岩石试件非线性蠕变模型及其稳定性分析[J]. 岩石力学与工程学报, 2004, 23(10): 1640-1642.
WANG Laigui, HE Feng, LIU Xiangfeng, et al. Nonlinear creep model and stability analysis of rock[J]. Chinese Journal of Rock Mechanics and Engineering, 2004, 23(10): 1640-1642.
[5] 曹树刚, 边金, 李鹏. 岩石蠕变本构关系及改进的西原正夫模型[J]. 岩石力学与工程学报, 2002, 21(5): 632-634.
CAO Shugang, BIAN Jin, LI Peng. Rheologic constitutive relationship of rocks and a modified model[J]. Chinese Journal of Rock Mechanics and Engineering, 2002, 21(5): 632-634.
[6] 陈沅江, 潘长良, 曹平, 等. 软岩流变的一种新力学模型[J]. 岩土力学, 2003, 24(2): 209-214.
CHEN Yuanjiang, PAN Changliang, CAO Ping, et al. A new mechanical model for soft rheology[J]. Rock and Soil Mechanics, 2003, 24(2): 209-214.
[7] 夏才初. 统一流变力学模型的若干问题研究[C]//中国岩石力学与工程学会. 第六次全国岩石力学与学术大会论文集. 北京: 科学出版社, 2000: 199-202.
XIA Caichu. A study on some problem of unitized rheology model[C]//Chinese Society for Rock Mechanics and Engineering. Proceeding of the 6th Rock Mechanics and Engineering Conference. Beijing: Science Press, 2000: 199-202.
[8] 夏才初, 许崇帮, 王晓东, 等. 统一流变力学模型参数的确定方法[J]. 岩石力学与工程学报, 2009, 28(2): 425-532.
XIA Caichu, XU Chongbang, WANG Xiaodong, et al. Method for Parameters determination with unified Rheological mechanical model[J]. Chinese Journal of Rock Mechanics and Engineering, 2009, 28(2): 425-532.
[9] 袁海平, 曹平, 许万忠, 等. 岩石黏弹塑性本构关系及改进的Burgers蠕变模型[J]. 岩土工程学报, 2006, 28(6): 796-799.
YUAN Haiping, CAO Ping, XU Wanzhong, et al. Visco-elasto-plastic constitutive relationship of rock and modified Burgers creep model[J]. Chinese Journal of Geotechnical Engineering, 2006, 28(6): 796-799.
[10] 佘成学, 崔旋. 高孔隙水压力对岩石蠕变特性的影响[J]. 岩石力学与工程学报, 2010, 29(8): 1603-1609.
SHE Chengxue, CUI Xuan. Influence of high pore water pressure on creep properties of rock[J]. Chinese Journal of Rock Mechanics and Engineering, 2010, 29(8): 1603-1609.
[11] 邢福东, 朱珍德, 刘汉龙, 等. 高围压高水压作用下脆性岩石强度变形特性试验研究[J]. 河海大学学报: 自然科学版, 2004, 32(2): 184-187.
XING Fudong, ZHU Zhende, LIU Hanlong, et al. Experimental study on strength and deformation characteristics of brittle Rocks under high confining pressure and Hydraulic pressure[J]. Journal of Hohai University :Natural Science, 2004, 32(2): 184-187.
[12] 孙钧. 岩石流变力学及其工程应用研究的若干进展[J]. 岩石力学与工程学报, 2007, 26(6): 1081-1106.
SUN Jun. Rock rheological mechanics and its advance in engineering applications[J]. Chinese Journal of Rock Mechanics and Engineering, 2007, 26(6): 1081-1106.
[13] 李亚丽, 于怀昌, 刘汉东. 三轴压缩下粉砂质泥岩蠕变本构模型研究[J]. 岩土力学, 2012, 33(7): 2035-2040.
LI Yali, YU Huaichang, LIU Handong. Study of creep constitutive model of silty Mudstone under triaxial compression[J]. Rock and Soil Mechanics, 2012, 33(7): 2035-2040.
[14] 李青麒. 软岩蠕变参数的曲线拟合计算方法[J]. 岩石力学与工程学报, 1998, 17(5): 559-564.
LI Qingqi. Curve fitting method for creep Parameter of soft rock[J]. Chinese Journal of Rock Mechanics and Engineering, 1998, 17(5): 559-564.
[15] 王来贵, 赵娜, 何峰, 等. 岩石蠕变损伤模型及其稳定性分析[J]. 煤炭学报, 2009, 34(1): 69-74.
WANG Laigui, ZHAO Na, HE Feng, et al. RockCreep damage model and its stability analysis[J]. Journal of China Coal Society, 2009, 34(1): 69-74.
[16] 佘成学, 崔璇. 岩石非线性蠕变模型[J]. 武汉大学学报: 工学版, 2009, 42(1): 25-28.
SHE Chengxue, CUI Xuan. Research on Nonlinear creep model of rock[J]. Journal of Wuhan University: Engineering, 2009, 42(1): 25-28.
(编辑 陈爱华)
收稿日期:2013-08-28;修回日期:2013-11-25
基金项目:国家自然科学基金资助项目(41302223);中央高校研究生创新基金资助项目(CDJXS12200004);重庆市基础与前沿研究计划项目(cstc2013jcyjA90004);重庆科技学院教授、博士生导师启动基金资助项目(CK2013B27)
通信作者:蒋海飞(1982-),男,安徽合肥人,博士研究生,从事岩石力学理论与工程研究;电话:15320346970;E-mail:jhfworld@163.com