Trans. Nonferrous Met. Soc. China 23(2013) 543-547
Thermodynamic approach to synthesis of silver nanocrystalline by mechanical milling silver oxide
Gholam Reza KHAYATI1, Kamal JANGHORBAN2
1. Department of Material Science and Engineering, Shahid Bahonar University of Kerman, P. O. Box 76135-133, Kerman, Iran;
2. Materials Science and Engineering Department, School of Engineering, Shiraz University, Zand Avenue, Shiraz, Iran
Received 7 March 2012; accepted 16 April 2012
Abstract: Thermodynamic analysis of the possibility of silver nanocrystalline preparation by high energy milling silver oxide was investigated. The molar Gibbs free energy function of mechanically activated samples was calculated from the structural defects such as amorphization, dislocation and surface energy. According to the molar Gibbs free energy function, the equilibrium temperature of mechanical reduction of silver oxide milled for 21 h was estimated at about 304 K. Consequently, at this temperature silver oxide cannot be stable and will transform to silver during the milling.
Key words: silver nanocrystalline; silver oxide; Gibbs free energy function; mechanical activation
1 Introduction
Mechanochemistry is a branch of science dealing with the chemical and physicochemical changes of materials due to the effect of mechanical energy [1]. Recently, mechanochemistry has been widely applied in many fields, such as preparation of intermetallic compounds, composites and complex oxides, nanocrystalline substances and nanomaterials [2-5]. According to the literature, the science base of mechanochemistry suffers from conceptual principles [6-9], especially the thermodynamics. Hence, finding a set of systematic and appropriate theory to explain the thermodynamic of mechanochemical process may be very useful.
During the mechanical milling over a very short time and space scale, the reactants may emit radiations to form a special plasmatic state and start chemical reaction under the action of great quantity of energy which is set free at the high-speed impacts. Once this step is over, the systematic energy drops rapidly and then structure relaxation occurs, where the rest energy is accumulated in solid in the form of structural disordering and structural mobility [10-12]. During mechanical treatment, non-equilibrium intermediate phase may be created [6,13] and consequently the formation of final product may lag behind the structural changes. Thus, in order to better explain the thermodynamic process of mechanochemical reaction, besides considering the classical chemical reaction thermodynamic, the thermodynamic of structural evolution should be employed as well.
In this study, the fundamental thermodynamic relations are proposed to impose in mechanochemical research areas, aiming to improve the conceptual principles of mechanochemical reaction thermodynamics. Taking for an example, the mechanochemical preparation of silver nanocrystalline by high energy ball milling silver oxide powders, and the thermodynamic analysis of the possibility of transformation are investigated.
2 Experimental
Ag2O powders (99%, 5-40 μm) were used as starting materials for mechanical milling in a planetary ball mill. Details of ball milling process are given in Table 1. The phase identification and structural changes of the products were investigated by Philips PW-1730 X-ray diffractometer (XRD) using Cu Kα radiation. The line broadening owing to the instrument was computed from Warren’s method [14]. Peak position (2θ), the full-width at half maximum (FWHM), and area under peak (A) were obtained from the XRD spectra. The OriginPro 8 software was used to obtain these parameters, among which the Ag2O planes were selected for the profile analysis.
Table 1 Details of ball mill machine and milling conditions
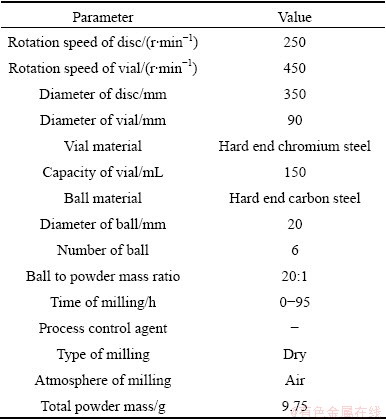
3 Results and discussion
Figure 1 shows the XRD patterns of milled samples with milling time. The patterns of powders milled up to 20 h show only the presence of Ag2O phase. During the first 20 h of milling, the peak intensity was decreased due to the decrease of the size of silver oxide crystallites. The traces of silver could be observed after 21 h milling.
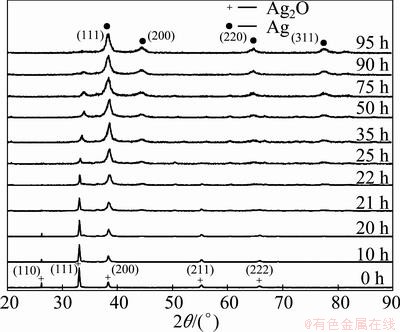
Fig. 1 XRD patterns of milled samples as function of milling time
Backscattered electron image of milled powders after 21 h in Fig. 2 qualitatively confirmed the presence of Ag particles by contrast phases between Ag (bright spots) and Ag2O (gray flakes). Also, the Ag2O particles were crashed and displayed brittle fracture surfaces that are the characteristics of brittle ionic crystals. While, the Ag particles were generally round and spherical in shape and displayed more homogenous size distribution compared with Ag2O particles.

Fig. 2 Backscattered electron image of milled powders after 21 h
According to the literature, the energetic condition of mechanically activated materials could be generally explained by the following structural defects [15]: the specific energy of dislocation density, the energy of amorphization, the specific energy of surface area to the surroundings or to a second phase.
The contribution of amorphization energy to the total energy changes is 93%-98.5%. Similar energy distributions are reported for quartz, calcite, magnesite, kaolinite, iron and periclase [16].
3.1 Calculation of specific energy of dislocation density
The classical energy balance observations of Griffith on crack propagation of an elastically isotropic substance show a functional relationship between the critical tensile stress of crack propagation and crack length. Other studies suggested that such ideal behavior does not apply to the majority of crack sensitive materials and must be modified [17]. The modifications of Griffith’s ideas for mechanical activation condition can result in a recast relation in terms of fracture mechanics concepts [18].
 (1)
(1)
where KIC is the critical stress intensity factor for crack propagation; Y is a geometrical factor related to the shape of the crack; σc is the critical tensile stress for crack propagation; a is the crack length. According to Eq. (1), by decreasing the crack length, the tensile stress of crack propagation increases. Hence, primary fracture and size reduction of silver oxide occur by propagation of the largest cracks at relative low σc. With increasing the stored energy by milling, the particle and its crack length decrease to micron or submicron in which σc becomes very large. Consequently, rather than fracture, generation of dislocations is the predominant phenomenon in mechanical activation [18].
The change in molar Gibbs free energy of milled silver oxide due to dislocations, ΔGd, is a function of molar enthalpy of dislocations, ΔHd, and molar entropy of dislocations, ΔSd, as Eq. (2) [18]
ΔGd =ΔHd-TΔSd (2)
According to Cottrell hypothesis, dislocations are essentially one-dimensional defects, and estimation was proposed that their entropy effect is significantly small. Therefore, T△Sd becomes negligible with respect to △Hd [19]. Hence, ΔGd is almost equal to Eq. (3):
 (3)
(3)
where b is the Burgers vector of the dislocation; μs is the elastic shear modulus; MV is the molar volume; ρ is the dislocation density [18]. The direction of Burger's vector of silver oxide is similar to cuprite [18,20]. Thus, the value of Burger’s vector for silver oxide in direction (100) is found to be 4.81×10-10 m [20]. MV=3.245×10-5 m3/mol is the molecular mass of silver oxide, 231.735×10-3 kg/mol, divided by its density, 7140 kg/m3, [15,21]. In order to determine the μs, the value of elastic modulus of silver oxide, E, must be calculated using
E=3K(1-2ν) (4)
where K is the bulk modulus of Ag2O (74 GPa), and ν is Poisson ratio and is about 0.3 [18,22]. From Eq. (4) elastic modulus of Ag2O is estimated to be 88.8 GPa. Consequently, the μs of Ag2O is calculated to be 34.2 GPa using
μs=E/2(1+v) (5)
The dislocation density ρ was calculated from the relationship ρ=<ρDρε>0.5, where ρD=(3/D2) (dislocation due to domain size), ρε=k(ε2)/b2 (dislocation due to lattice strain); D is the crystallite size; k is a material constant of about 2; ε is the lattice strain; b is the Burger’s vector. The average crystallite size and internal strain were calculated using Williamson–Hall plot [23].
Figure 3 shows the changes in crystallite size and lattice strain with milling time. Clearly, one can decompose the time dependence of the microstructure in two domains.
For time up to 20 h, the crystallite size of Ag2O decreases rapidly to a value near 23 nm as a result of mechanical shocks induced by the milling process. At the same time, the strain increases to 0.75%. During the first 20 h, the energy provided by the milling was consumed to generate the crystal imperfections such as dislocations and grain boundaries.
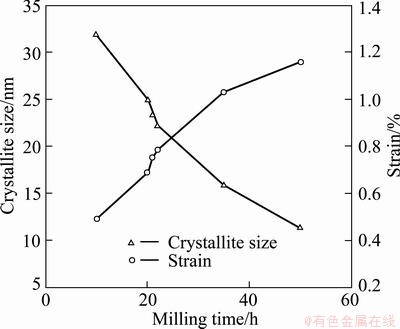
Fig. 3 Evolutions of size and strain with milling time
Between 21 h and 50 h, after preparation of Ag crystallites, the rate of size decreasing and the rate of strain increasing of Ag2O crystallites are decreased as a result of thermal annealing. In other words, as expected the strain should increase with milling time because the material is put under increasing stress. Simultaneously, the temperature within the vial rises and the thermal energy anneals the sample, namely, the strain reduces. If one of these two parameters dominates, the time dependence of strain and size would be more drastic than the observed one. So it seems that under the specific conditions of our synthesis, increasing temperature relatively decreases the rates of changes of size and strain with milling time.
3.2 Calculation of amorphization energy
The degree of crystallinity (DOC) is defined as
DOC=(At/A0) (6)
where A0 and At are the areas under the (111) plane diffraction peak of non-activated and activated samples in time t, respectively [24,25]. Thus, the amorphization energy of milled Ag2O could be calculated from
 (7)
(7)
where 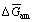 is the molar amorphization energy of Ag2O and can be estimated as follows [18]:
is the molar amorphization energy of Ag2O and can be estimated as follows [18]:
 (8)
(8)
 where
where  is the molar enthalpy of melting Ag2O at Tm. Although the value of
is the molar enthalpy of melting Ag2O at Tm. Although the value of  is unknown due to the decomposition of Ag2O at about 553 K, since the crystal structure of Cu2O is similar to Ag2O, the enthalpy change in melting Ag2O can be assumed to be the same as that of Cu2O (56.9 kJ/mol) [26], consequently:
is unknown due to the decomposition of Ag2O at about 553 K, since the crystal structure of Cu2O is similar to Ag2O, the enthalpy change in melting Ag2O can be assumed to be the same as that of Cu2O (56.9 kJ/mol) [26], consequently:
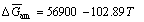 (9)
(9)
3.3 Calculation of specific energy of surface area to surroundings or to a second phase
The surface energy of particles in thermodynamics is estimated from [1]
△Gsurf=σ△A (10)
where σ is the specific surface and △A is the change of overall surface energy of a solid. It was estimated for mechanical activation of ionic crystals that the surface energy, △Gsurf, corresponds approximately to 10% of overall Gibbs energy of mechanically activated samples [1], thus
△Gsurf=0.1(△Gam+△Gd) (11)
3.4 Calculation of molar Gibbs free energy of mechanically activated Ag2O
The following reaction has been considered to estimate the molar Gibbs free energy of milled silver oxide:
Ag2O(s)=2Ag(s)+(1/2)O2(g) (12)
where the standard Gibbs free energy of reaction (12) is [7]
 (13)
(13)
Consequently, at the atmosphere pressure, p(O2)=21.27825 kPa, the Gibbs free energy change of non- activated Ag2O was estimated from
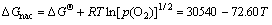 (14)
(14)
The molar Gibbs free energy change of mechanically activated Ag2O after time t, i.e. ΔGT, can be calculated from Eq. (15) [1]
 (15)
(15)
where △Gac is estimated from
 (16)
(16)
Consequently, ΔGT is computed from.
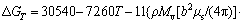
 (17)
(17)
The values of ρ and A21/A0 of the sample milled for 21 h are measured to be 7.31×1014 m2 and 0.91, respectively. Figure 4 shows the ΔG values of non-activated and mechanically activated samples milled for 21 h with temperature according to Eqs. (15) and (17). As shown, the equilibrium temperature of the 21 h-milled sample was 304 K. Accordingly, between 304 to 461 K, the Gibbs free energy change of reaction (12) in mechanically activated condition was negative while the Gibbs free energy change of unmilled sample was positive. Thus, by extending the milling time the Ag2O phase is not stable and the reaction proceeds toward the formation of Ag. This result was also confirmed by the vial temperature after 21 h milling that was measured by thermometer at about 305 K.
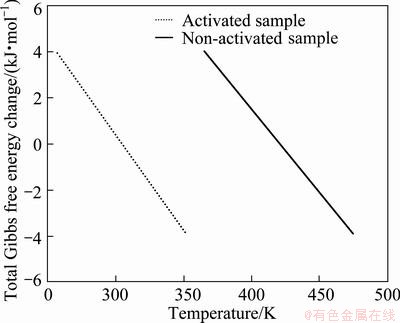
Fig. 4 Total Gibbs free energy of mechanochemical reaction before and after 21 h milling
4 Conclusions
The thermodynamic principles of mechanochemical reaction were investigated using fundamental thermodynamic relations. Mechanochemical reduction of Ag2O was studied as a case. According to the calculated total Gibbs free energy function of mechanochemical reaction after 21 h milling, the transformation temperature is about 304 K. The negative value of ΔG near 304 K shows that the formation of silver has started a few moment before the 21 h milling and the reduction reaction proceeds toward the production of silver. The results showed that the amorphization energy was the most affecting parameter on Gibbs free energy function of mechanically activated Ag2O.
References
[1] BALAZ P. Mechanochemistry in nanoscience and minerals [M]. Berlin: Springer-Verlag, 2008: 18.
[2] WIECZOREK-CIUROWA K, GAMRAT K. Some aspects of mechanochemical reactions [J]. Mater Sci Poland, 2007, 25: 219-232.
[3] KHAYATI G R, JANGHORBAN K. The nanostructure evolution of Ag powder synthesized by high energy ball milling [J]. J Adv Powder Technol, 2012, 23(3): 393-397.
[4] KHAYATI G R, JANGHORBAN K. An investigation on the application of process control agents in the preparation and consolidation behavior of nanocrystalline silver by mechanochemical method [J]. Adv Powder Technol, 2012, 23(6): 808-813.
[5] KHAYATI G R, JANGHORBAN K, SHARIAT M H. Isothermal kinetic study of mechanochemically and thermally synthesized Ag from Ag2O [J]. Transactions of Nonferrous Metals Society of China, 2012, 22(4): 935-942.
[6] IVANOV E, SURYANARAYANA C. Materials and process design through mechanochemical routes [J]. Mater Synth Process, 2000, 8: 235-244.
[7] KONOPKA M, TURANSKY R, REICHERT J, FUCHS H, MARX D, STICH I. Mechanochemistry and thermochemistry are different, stress-induced strengthening of chemical bonds [J]. Phys Rev Lett, 2008, 100: 115503-115507.
[8] ROSEN B M, PERCEC V. Mechanochemistry: A reaction to stress, [J]. Nature, 2007, 446: 381-382.
[9] BOLDYREV V V. Mechanochemistry and mechanical activation of solids [J]. Russ Chem Rev, 2006, 75(3): 177-189.
[10] BUTYAGIN P Y. Disordered structures and mechanochemical reactions in solids [J]. Uspechi Chimiji, 1984, 53: 1769–1781.
[11] CHEN Zhen-hua, CHEN Ding. Mechanical alloying and solid-liquid reaction milling [M]. Beijing: Chemical Industry Press, 2006: 439. (in Chinese)
[12] MILOSEVIC S, RISTIC M M. Thermodynamics and kinetics of the mechanical activation of materials [J]. Sci Sinter, 1998, 30: 29.
[13] BOLDYREV V V, TKAKOVA K. Mechanochemistry of solids: Past, present, and prospects [J]. Mater Synth Process, 2000, 8: 121-132.
[14] CULLITY B D, STOCK S R. Elements of X-ray diffraction [M]. NJ: Prentice Hall, Upper Saddle River, 2001: 399.
[15] HEEGN H, BIRKENEDER F, KAMPTNER A. Mechanical activation of precursors for nanocrystalline materials [J]. Cryst Res Technol, 2003, 38: 7–20.
[16] POURGHAHRAMANI P, FORSSBERG E. Comparative study of microstructural characteristics and stored energy of mechanically activated hematite in different grinding environments [J]. Int Miner Process, 2006, 79: 120-139.
[17] DIETER G E. Mechanical metallurgy [M]. 3rd ed, McGraw-Hill. 2001: 430.
[18] TROMANS D, MEECH J A. Enhanced dissolution of minerals: Stored energy, amorphism and mechanical activation [J]. Miner Eng, 2001, 14: 1359-1377.
[19] COTTRELL A H. Dislocations and plastic flow in crystals [M]. Oxford University, 1958: 37.
[20] PEI F, WU S, WANG G, XU M, WANG S, CHEN L. Electronic and optical properties of noble metal oxides M2O (M=Cu, Ag and Au): First-principles study [J]. Korean Med Sci, 2009, 55(3): 1243-1249.
[21] LIDE D R. Handbook of chemistry and physics [M]. Boca Raton, FL: CRC Press, 1998: 4.
[22] GEBRANDE H. Elastic wave velocities and constants of elasticity of rocks at room temperature and pressures <1 GPa [M]. Springer Materials, The  Database: (http://www. sprigermaterials.com), 1982: 1.
Database: (http://www. sprigermaterials.com), 1982: 1.
[23] WILLIAMSON K, HALL W H. X-ray line broadening from filed aluminum and wolfram [J]. Acta Metall, 1953, 1: 22–31.
[24] PALANIANDY S, AZIZLI M K A. Mechanochemical effects on talc during fine grinding process in a jet mill [J]. Inter Miner Process, 2009, 92: 22–33.
[25] ARBAIN R, OTHMAN M, PALANIANDY S. Preparation of iron oxide nanoparticles by mechanical milling [J]. Miner Eng, 2011, 24(1): 1–9.
[26] PARK J H, MIN D J. Quantitative analysis of the relative basicity of CaO and BaO by silver solubility in slags [J]. Metall Mater Trans B, 1999, 30(4): 689-694.
机械球磨氧化银制备银纳米晶的热力学分析
Gholam Reza KHAYATI1, Kamal JANGHORBAN2
1. Department of Material Science and Engineering, Shahid Bahonar University of Kerman,P. O. Box No. 76135-133, Kerman, Iran;
2. Materials Science and Engineering Department, School of Engineering, Shiraz University, Zand Avenue, Shiraz, Iran
摘 要:对高能球磨氧化银制备银纳米晶的可行性进行热力学分析。根据结构缺陷如非晶化、位错和表面能,计算机械活化样品的摩尔吉布斯自由能函数。根据摩尔吉布斯自由能函数,计算得到机械球磨21 h还原氧化银的平衡温度约为304 K。在304 K下,氧化银不稳定,在球磨过程中会还原成银。
关键词:银纳米晶;氧化银;吉布斯自由能函数;机械活化
(Edited by Hua YANG)
Corresponding author: Gholam Reza KHAYATI; Tel: 0098-915-1903477, Fax: 0098-341-2111860; E-mail: rezakhayyati@yahoo.com
DOI: 10.1016/S1003-6326(13)62497-8