Trans. Nonferrous Met. Soc. China 22(2012) 164-169

3D modeling and deformation analysis for electromagnetic sheet forming process

CUI Xiao-hui, MO Jian-hua, ZHU Ying

State Key Laboratory of Material Processing and Die & Mould Technology,

Huazhong University of Science and Technology, Wuhan 430074, China

Received 29 December 2010; accepted 17 March 2011

Abstract: Electromagnetic forming (EMF) is a high-speed forming method which can be quite effective in increasing the forming limits of metal sheet. However, the EMF process is complicated due to magnetic-structure coupling analysis. Numerical simulation offers an opportunity to overcome the problem. Nevertheless, most present models for EMF process are limited to 2D axisymmetric model. So, a three-dimensional (3D) finite element model was established to analyze the electromagnetic sheet bulging. The contact between the sheet and the die and the effect of sheet deformation on the magnetic field analysis were both taken into consideration during the forming process. The simulation results of deflection at the sheet center and 20 mm away from the center were in agreement with the experimental ones. The plastic strain energy and plastic strain were analyzed.

Key words: electromagnetic forming; high velocity forming; numerical simulation; finite element mode; magnetic force

1 Introduction

Electromagnetic forming (EMF) is one of the high-speed forming methods. During the EMF process, the discharge current runs through a coil which produces intense transient magnetic field around it. According to Faraday's law of electromagnetic induction, when the metal work piece is placed on a magnetic field, eddy current will be produced on the surface. The two currents flow in the opposite direction and a large magnitude magnetic repulsion force is created between the coil and the workpiece. This force is used to launch the workpiece at a very high speed [1, 2]. Since the electromagnetic forming process can promote significant increases in strain to failure in low-ductility materials due to high strain rate and inertial effect, which can improve the formability of metal plate and reduce spring-back and wrinkling [3-5].

During the past few years, researchers mainly adopted experimental and numerical study for EMF process. The pioneer work on the electromagnetic forming process was presented by AL-HASSANI [6]. He analyzed magnetic pressure distribution caused by different coils on flat plates. Then, IMBERT et al [7] analyzed the effect of tool-sheet interaction on damage evolution in electromagnetic forming from the work by AL-HASSANI [6]. TAKATSU et al [8] carried out both experiment a and numerical study on the high-speed free forming of a clamped circular disk in an electromagnetic forming process. The numerical results showed fairly good agreement with the experiment ones.

With the development of commercial finite element codes, some approaches have been proposed. FENTON and DAEHN [9] used a two-dimensional (2D) arbitrary Lagrangian Eulerian (ALE) finite-difference computer code to predict electromagnetic sheet metal forming process. Their results coincided with the experimental data. In order to get a more precise simulation result, the effect of workpiece deformation on magnetic analysis must be considered. YU et al [10-12] adopted a sequential coupling method to analyze electromagnetic tube compression process. The simulation results were accurate due to considering the effect of the tube deformation on the electromagnetic field analysis. BARTELS et al [13] demonstrated that the simple loose-coupled approach can only be used as a good approximation for relatively fast deformation process and small displacement. Otherwise, the more accurate sequential-coupled model which considers the effect of the workpiece deformation should be used. But the sequential coupling method was mainly used in tube forming.

Up to now, modeling approaches established for EMF process in the literature are mainly restricted to 2D models. By drawing a comparison between the 2D and 3D simulation results, BAHMANI et al [14] found an increase of about 15% in the amplitude of the magnetic flux density. Moreover, for industrial applications, the modeling of 3D forming operation becomes crucial for an effective process design.

In this work, a three-dimensional (3D) finite element model and sequential coupling method are used to simulate the electromagnetic sheet free bulging according to the experimental results. The contact between the sheet and the die, and the effect of sheet deformation on the magnetic field analysis are both taken into consideration during the forming process.

2 Flowchart of simulation method

The schematic flowchart of the simulation method is illustrated in Fig. 1. In each time step, ANSYS/EMAG is used to model the time—current curves in order to obtain the transient magnetic forces generated on the sheet. The forces are then used as loading condition to predict the high-rate deformation using ANSYS/ MECHANICAL code. Whereafter, the sheet geometry is updated according to the sheet deforming result. The deformed sheet is imported to ANSYS/MEAG again to calculate the magnetic forces in the next time step.

3 Three-dimensional finite element model

3.1 Electromagnetic field model

In order to prove the accuracy of the simulation method, the models and experimental results are cited from Ref. [8]. The experimental condition contains a 5-turn spiral coil. The coil separation is 5.5 mm. The thickness of the sheet is 0.5 mm. The distance between the sheet and the coil is 1.6 mm. The diameter of the sheet is 110 mm. Figure 2 shows the 3D model for electromagnetic field analysis. Figure 3 shows the detailed region including the coil and the sheet (1/4 model). The surrounding air is meshed in order to propagate the magnetic field generated by the coil. To improve the accuracy of numerical simulation, the air is divided into many hexahedrons.

3.2 Structural field model

The forces calculated by ANSYS/MEAG are used as boundary condition to the ANSYS/MECHANICAL software, an implicit dynamic finite element code, which is used in sheet deformation analysis. The transient dynamic equilibrium equation and the Newmark time integration method are used to solve it.

                          (1)

where M is the structural mass matrix; C is the structural damping matrix; u is the nodal displacement vector; K is the structure stiffness matrix; F^a is the load vector.

When a complicated three dimensional model is considered, implicit method requires a relatively large amount of computer time to calculate the structural mass matrix, which may cause convergence problem. So, the value of penalty stiffness is increased to overcome the convergence problem.

4 Simulation result analysis

As shown in Fig. 4, sheet forming is analyzed by using numerical simulation method, which provides finite element mesh deforming figures at different time steps. According to the deformed shape of the sheet, the geometry of electromagnetic model is updated. Since the simulation results show that the distortion is reasonable, it can improve the precision of magnetic field analysis.

Fig. 1 Flowchart of implemented algorithm

The contact conditions are considered between the die and the sheet as well as the sheet and holder during the simulation process. Therefore, the method can be used to large deformation analysis and contact analysis.

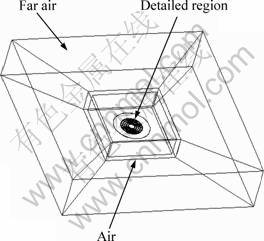
Fig. 2 3D model for electromagnetic field analysis

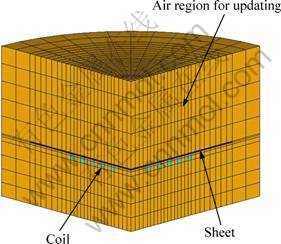
Fig. 3 Detailed region including coil and sheet

Figure 5 shows the changes of magnetic force on the sheet at different time. At the initial condition, the direction of magnetic force is almost perpendicular to the surface of the sheet. When the time is prolonged, the direction of the magnetic force varies with the change of sheet geometry. According to the simulation results of Fig. 4 and Fig. 5, we can conclude that the 3D simulation method overcomes the electromagnetic- structure coupling problem.

Figure 6 shows the deflection at the sheet center (r=0 mm) with time, and Figure 7 shows the deflection at  20 mm away from the center with time, in which the triangular marks are the experimental results [8], the dotted lines are the calculation results [8], and the solid lines are the present results. As shown in Fig. 6 and Fig. 7, the present results are slightly greater than the experimental ones. Moreover, the tendency of deformation using finite element method is in agreement with the experimental ones. However, the calculated results [8] are different from the experimental ones to some extent. Therefore, the method can better predict the electromagnetic forming process.

Figure 8 shows the velocity change with time. The deformation at 20 mm away from the center firstly arises due to the maximum pressure at this region. The center of the sheet is almost driven by surroundings, and moves later because the magnetic pressure is equal to zero at the sheet center. In the initial stage, opposite flowing direction is found at the center and 20 mm away from the center. Then the motions of the surrounding parts drive the sheet center to deform. So, the inertial force plays a key role in electromagnetic forming [15, 16]. With increasing the time, the magnetic force on the sheet reduces rapidly due to the gradual decay of the transient current and the increased distance between the coil and the sheet. The peak radial velocities at the center and a distance of 20 mm away from the center are 179 m/s and 108 m/s, respectively. The velocity shocks repeatedly between positive and negative after 220 μs.

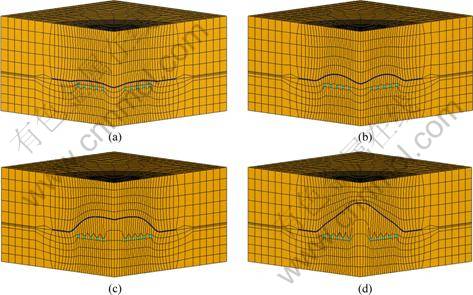
Fig. 4 Change of meshes in electromagnetic simulation at different time: (a) t=40 μs; (b) t=80 μs; (c) t=150 μs; (d) t=300 μs

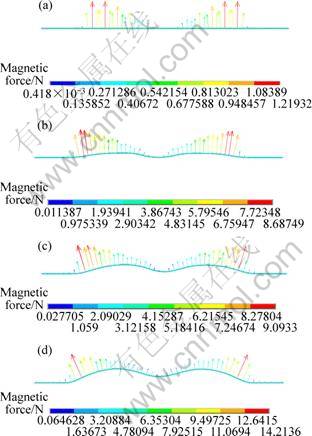
Fig. 5 Change of magnetic force on sheet at different time: (a) t=0 μs; (b) t=40 μs; (c) t=60 μs; (d) t=80 μs

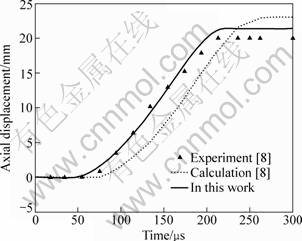
Fig. 6 Deflection of sheet center with time

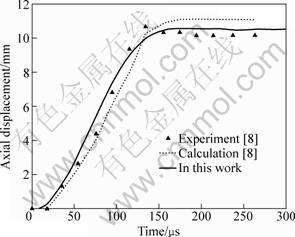
Fig. 7 Deflection at 20 mm away from center with time

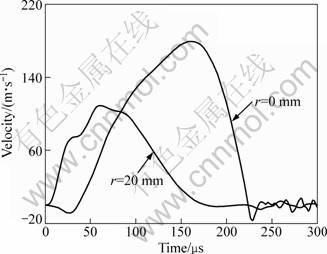
Fig. 8 Velocity changes with time

Figure 9 shows the changes of three plastic strain components: ε₁ (radial component), ε₂ (hoop component), ε₃ (axial component). The radial component is almost the same with the hoop component at the center. The radial component is greater than the hoop component at 20 mm away from the center. There are tensile strains in two directions at the center and 20 mm away from the center. As shown in Fig. 9, there is a negative velocity at the center before 40 μs. The plastic strain at the center is increasing before 50 μs. Therefore, the inertial force plays a leading role in the EMF process. From 50 μs to 150 μs, the plastic strain at the center stays the same, while plastic strain at 20 mm away from the center increases gradually. At the initial condition, the maximum magnetic force occurs at 20 mm away from the center. As shown in Fig. 5, the direction of the magnetic force varies with the change of sheet geometry. Resulting from this, the plastic strain of ε₁ is larger than ε₂ after 50 μs. From 150 μs to 220 μs, the plastic strain increases sharply at the center due to high speed changes. Then the plastic strain of the center stays the same after 220 μs due to the end of deformation.

Figure 10 shows the changes of strain rate with time at the center. There are two peak values in strain rate during the forming process. The first one occurs due to the extrusion force at the center before 40 μs. The second one occurs due to the high velocity. The maximum strain rate is 6890 s^-1.

Figure 11 shows the final plastic strain along radial direction. The maximum of plastic strain appearing at the center of the sheet is 0.472. Therefore, the failure may firstly occur in the center of the sheet due to high plastic

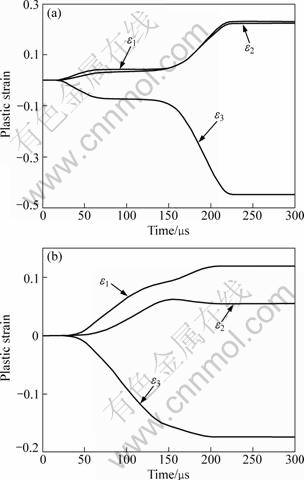
Fig. 9 Change of plastic strain at specified locations with time: (a) Change of plastic strain at center point; (b) Change of plastic strain at 20 mm away from center

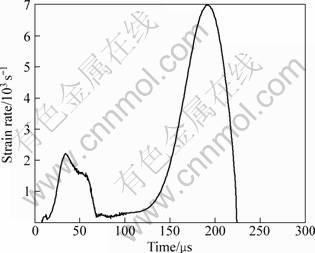
Fig. 10 Change of strain rate with time at center

strain. With increasing the sheet radius, the plastic strain becomes smaller. But the strain is slightly increased at a distance of about 40 mm away from the center. The reason why this happens is that frictional forces exist between the die and the sheet in this region. During electromagnetic sheet bulging, the failures mainly exist in the center and the die entry radius at the base of the part. This is in agreement with the simulation result    [7, 17]. In order to analyze the formability of metal plate, it requires damage-based constitutive equations. This is a goal to be achieved in the follow-up study.

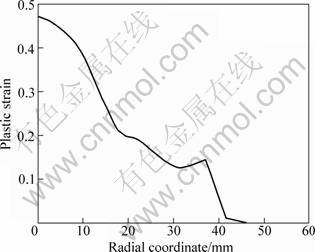
Fig. 11 Change of plastic strain along radial direction

Figure 12 shows the plastic strain energy of sheet deformation as a function of time. The value of discharge energy is 720 J. The plastic strain energy rapidly increases after 50 μs and remains the same after 220 μs. At the time of 300 μs, the plastic strain energy is 26.9 J and the energy utilization ratio is 3.73%. The efficiency of electromagnetic sheet bulging is much lower than that of electromagnetic tube forming [10]. Therefore, how to improve the energy utilization efficiency is another goal to be achieved in the follow-up study.

Fig. 12 Change of plastic strain energy with time

5 Conclusions

1) A three-dimensional finite element model is used to analyze the electromagnetic sheet bulging. The effect of sheet deformation on magnetic analysis and the contact between the sheet and the die are considered in electromagnetic model. The simulation results are in agreement with the experimental ones.

2) There are tensile strains in two directions at the center and 20 mm away from the center. The maximum plastic strain occurs at the center of the sheet. Therefore, the failure may firstly arise at the center. In order to analyze the formability of metal plate, it requires damage-based constitutive equations.

3) The plastic rate energy is 26.9 J and the energy efficiency is 3.73%. The energy efficiency is much lower than that of electromagnetic tube forming.

4) The 3D finite element model can also be used to form non-axisymmetrical parts, which provides a rational method for industrial application.

References

[1] MAMALIS A G, MANOLAKOS D E, KLADAS A G. KOUMOUTSOS A K. Electromagneitc forming and powder processing: Trends and developments [J]. Applied Mechanics Reviews, 2004, 57(4): 299-324.

[2] CORREIA J P M, SIDDIQUI M A, AHZI S, BELOUETTAR S, DAVIES R. A simple model to simulate electromagnetic sheet free bulging process [J]. International Journal of Mechanical Sciences, 2008, 50: 1466-1475.

[3] MAMALIS A G, MANOLAKOS D E, KLADAS A G, KOUMOUTSOS A K. Electromagnetic forming tools and processing conditions: Numerical simulation [J]. Materials and Manufacturing Processes, 2006, 21: 411-423.

[4] HAN Fei, MO Jian-hua, HUANG Shu-huai. Theoretical study and application of electromagnetic forming technology [J]. Forging and Stamping Technology, 2006, 31(6): 4-8. (in Chinese)

[5] SETH M, VOHNOUT V J, DAEHN G S. Formability of steel sheet in high velocity impact [J]. Journal of Material Processing Technology, 2005, 168(3): 390-400.

[6] Al-HASSANI S T S. Magnetic pressure distribution in the sheet metal forming [C]//Electrical Methods of Machining, Forming and Coating, Institute of Electrical Engineering Conference, 1975: 1-10.

[7] IMBERT J M, WRINKLER S L, WORSWICK M J, OLIVERIA D A, GOLOCASHCHENKO S. The effect of tool-sheet interaction on damage evolution in electromagnetic forming of aluminum alloy sheet [J]. Journal of Engineering Materials and Technology, 2005, 127: 145-153.

[8] TAKATSU N, KATO M, SATO K, TOBE T. High-speed forming of metal sheets by electromagnetic force [J]. Japan Society of Mechanical Engineers International Journal: Series Ш, 1988, 31(1): 142-148.

[9] FENTON G K, DAEHN G S. Modeling of electromagnetically formed sheet metal [J]. Journal of Materials Processing Technology, 1998, 75: 6-16.

[10] YU H P, LI C F, DENG J H. Sequential coupling simulation for electromagnetic mechanical tube compression by finite element analysis [J]. Journal of Materials Processing Technology, 2009, 209: 707-713.

[11] YU H P, LI C F. Effects of current frequency on electromagnetic tube compression [J]. Journal of Materials Processing Technology, 2009, 209: 1053-1059.

[12] YU Hai-ping, LI Chuan-feng. Effects of coil length on tube compression in electromagnetic forming [J]. Transactions of Nonferrous Metals Society of China, 2007, 17(6): 1270-1275.

[13] BARTELS G, SCHATZING W, SCHEIBE H P, LEONE M. Comparison of two different simulation algorithms for the electromagnetic tube compression [J]. International Journal of Material Forming, 2009, 2: 693-696.

[14] BAHMANI M A, NIAYESH K, KARIMI A. 3D simulation of magnetic field distribution in electromagnetic forming systems with field-shaper [J]. Journal of Materials Processing Technology, 2009, 209: 2295-2301.

[15] HUANG Shang-yu, CHANG Zhi-hua, WANG Zhong-ren, WANG Li-feng, YANG Mei. A finite element analysis of electromagnetic sheet metal expansion process [J]. Transactions of Nonferrous Metals Society of China, 1998, 8(3): 490-495.

[16] WANG L, CHEN Z Y, LI C X, HUANG S Y. Numerical simulation of the electromagnetic sheet metal bulging process [J]. The International Journal of Advanced Manufacturing Technology, 2006, 30: 395-400.

[17] OLIVEIRA D A, WORSWICK M J, FINN M, NEWMAN D. Electromagnetic forming of aluminum alloy sheet: Free-form and cavity fill experiments and model [J]. Journal of Materials Processing Technology, 2005, 170: 350-362.

电磁平板自由胀形3D数值模拟

崔晓辉，莫健华，朱 莹

华中科技大学 材料成形与模具技术国家重点实验室，武汉 430074

摘  要：电磁成形是一种高速率成形方法，它能够有效提高金属板材的成形极限。但是电磁成形过程复杂，涉及到磁场-结构场之间的耦合分析。数值模拟提供一种手段去解决耦合问题。然而，大多数的数值模拟都限于2D。建立3D有限元模型去分析电磁平板胀形。成形过程中考虑了板料与底模的接触和板料变形对磁场的影响。板料中心节点和半径20 mm处节点的位移随着时间的变化与实验结果一致。分析了塑性应变能和塑性应变。

关键词：电磁成形；高速率成形；数值模拟；有限元模型；电磁力

(Edited by YANG Hua)

Foundation item: Project (50875093) supported by the National Natural Science Foundation of China

Corresponding author: CUI Xiao-hui; Tel: +86-13477081759; E-mail: cuixh_hust@163.com

DOI: 10.1016/S1003-6326(11)61156-4