
DOI: 10.11817/j.issn.1672-7207.2019.10.013
基于SHEPWM阶段控制的航空电磁发射波形研究
于生宝1,高丽辉1,陈楠1,黄勇2
(1. 吉林大学 仪器科学与电气工程学院,吉林 长春,130026;
2. 吉林省博安智能科技有限公司,吉林 长春,130013)
摘要:为保证低开关频率条件下发射电流质量,提出半周期镜像对称选择性谐波消除脉冲宽度调制(SHEPWM)阶段控制策略来平衡发射电流质量与开关损耗。基于发射电流及发射线圈阻感负载的时频域信息,建立半周期镜像对称SHEPWM阶段控制非线性超越方程组,利用神经网络递归算法求解出对应交变梯形波电流的开关时刻序列。仿真和实验验证表明:半周期镜像对称SHEPWM阶段控制策略在保证发射波形质量及探测精度的前提下,能有效降低开关损耗。
关键词:时间域航空电磁法;选择性谐波消除脉冲宽度调制技术(SHEPWM);非线性超越方程组;神经网络;傅里叶变换;阶段控制;开关损耗
中图分类号:P631 文献标志码:A 开放科学(资源服务)标识码(OSID)
文章编号:1672-7207(2019)10-2446-09
Research on airborne electromagnetic emission waveform via SHEPWM subsection control
YU Shengbao1, GAO Lihui1, CHEN Nan1, HUANG Yong2
(1. College of Instrumentation and Electrical Engineering, Jilin University, Changchun 130026, China;
2. Jilin Province Bo'an Intelligent Technology Limited Company, Changchun 130013, China)
Abstract: To ensure the quality of the transmitting current under the low switching frequency condition, a semi-periodic mirror symmetry selective harmonic elimination pulse width modulation(SHEPWM) subsection control approach was proposed to balance transmitting current quality and switching loss. Semi-periodic mirror symmetry SHEPWM nonlinear equations were established based on the time-frequency domain information of transmitting current and transmitting coil, and then the neural network recursive algorithms was used to solve switching time series of trapezoidal wave current. The simulation and experimental results show that the semi-periodic mirror symmetry SHEPWM subsection control strategy can effectively reduce the switching loss on the basis of ensuring the quality of the transmitted waveform and the accuracy of the detection.
Key words: helicopter-borne time-domain electromagnetic method (HTEM); selective harmonic elimination pulse width modulation (SHEPWM); nonlinear transcendental equations; neural network; Fourier transform; subsection control; switching loss
直升机式航空时间域电磁法(helicopter-borne time-domain electromagnetic method, HTEM)是一种基于直升机的资源勘查的时间域电磁物探方法[1-2]。其原理是利用系统在发射线圈中产生交变电流,激发空间的一次电磁场,若地下含有电磁敏感矿体(如金属矿),则会产生二次感应场。系统由接收线圈获取二次感应电压,分析电压衰减情况可获得地下矿体的位置、形态和构造等信息。直升机方式探测效果接近地面方式,在崎岖地区的大面积、高效率的矿产资源勘查方面,有取代地面方式的趋势[3-6]。时间域航空电磁系统采用空中发射和接收的测量方式,与地面方法相比,航空发射系统有限蓄电能力要求逆变电源具有效率高、体积小和质量小等特点[7]。HTEM的物探效果与发射的梯形波电流质量密切相关,下降沿线性度越高,反向过冲越小,平顶端波形稳定性越好,越能更好地反映矿体近地表信息[8-9]。目前,国内外普遍采用脉冲宽度调制(pulse width modulation, PWM)控制方法获得双极性梯形波发射电流,提高载波频率可以有效改善发射波形质量,但载波频率提高意味着开关损耗增加,这将造成功率管发热严重、许用电流下降等不利影响,发射系统的效率也无法提高。为此,本文提出半周期镜像对称选择性谐波消除脉冲宽度调制(selective harmonic eliminated pulse width modulation, SHEPWM)技术阶段控制方法。该方法根据发射电流的时域特性建立SHEPWM非线性方程组的左侧多项式,基于发射电流及发射线圈阻感负载的频域信息建立SHEPWM非线性方程组的右侧多项式,从而得到控制发射电流频域特性(谐波幅值、相位和直流分量)及时域特性(上升沿、平顶端和下降沿)的半周期镜像对称SHEPWM阶段控制非线性超越方程组。选用神经网络算法获得对应交变梯形波的开关时刻序列,控制发射系统逆变器,得到平顶端稳定、下降沿无反向过冲以及开关损耗小的发射电流。
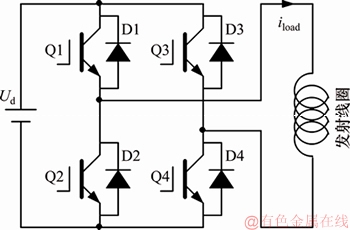
图1 HTEM发射电路框图
Fig. 1 Block diagram of HTEM transmitting circuit
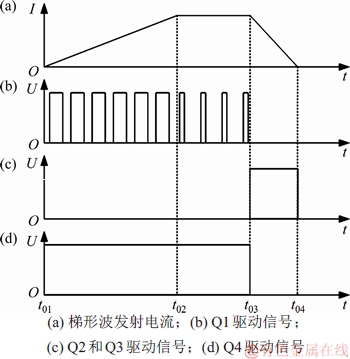
图2 发射电路驱动信号及输出电流波形
Fig. 2 Driving signal and transmitter current waveforms of launch system
1 半周期镜像对称SHEPWM阶段控制发射系统
1.1 发射电路工作过程
图1所示为HTEM发射电路框图。由图1可见:发射线圈为阻感负载,开关器件Q1,Q2,Q3和Q4的类型为绝缘栅双极型晶体管(insulated gate bipolar transistor, IGBT),开关器件和反并联二极管构成H桥电路,Q1和Q4及Q2和Q3交替导通,从而在发射线圈中产生交变的梯形波电流。
图2所示为发射电路驱动信号及输出电流波形。由于双极性梯形波电流在正向和负向的控制原理一样,因此,只对正向梯形波电流进行控制原理说明。由图2可见:t01~t02期间为电流上升沿控制阶段,开关器件Q1和Q4导通,控制Q1以一定开关频率与占空比进行开关,Q4常开,为发射线圈提供正向电压,使电流上升;t02~t03期间为电流平顶端控制阶段,保持Q4常开,调整Q1的占空比,使得输出电压减小,维持平顶端电流稳定;t03~t04期间为电流下降沿控制阶段,控制Q1和Q4关断,Q2和Q3常开,为发射线圈提供反向电源电压,使电流快速下降。
1.2 半周期镜像对称SHEPWM阶段控制方法
SHEPWM是一种控制逆变器输出波形谐波的重要技术,在许多应用领域如可再生能源系统和电力电子领域,被用来消除不必要的低阶谐波,提高逆变器的性能和效率。通过对逆变器输出的相电压进行傅里叶分解,强制其基波幅为期望值、选定的低频次谐波为零,建立非线性超越方程组,求解方程组来得到满足要求的开关切换角,并用这些开关切换角控制逆变器,实现所期望的正弦输出电压[10-12]。为了降低方程的复杂性,输出电压波形通常设置为1/4对称。然而,对于航空时间域电磁勘探,输出波形的谐波分量是有用信号,因此,在研究中,半周期镜像对称SHEPWM阶段控制方法被用来增强有用的谐波成分,消除不必要的谐波成分。
SHEPWM周期输出电压波形可以展开成收敛傅里叶级数形式,表示成直流分量、基频分量和一系列谐波分量的叠加:
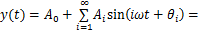
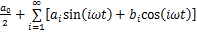 (1)
(1)
式中:y(t)为SHEPWM输出电压;A0为直流分量;i为谐波次数,i=1,2,3,…;Ai为谐波幅度; 为谐波相位;ω=2
为谐波相位;ω=2 f,为角频率;f为输出电压波形频率。ai,bi,a0,A0,Ai和
f,为角频率;f为输出电压波形频率。ai,bi,a0,A0,Ai和 有如下关系:
有如下关系:
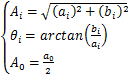 (2)
(2)
式(2)中的傅里叶系数ai和bi及直流分量a0可从下式中获得:
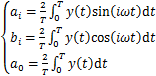 (3)
(3)
式中:T为输出电压波形周期,i=1, 2, 3, …。
图3所示为HTEM发射波形半周期镜像对称阶段控制。由图3(a)可见:HTEM的理想发射波形为双极性梯形波,具有半周期镜像对称特点,且0~t01,t04~T/2+t01和T/2+t04~T阶段发射电流为零,其中,t01=3.80 ms,t02=7.80 ms,t03=10.00 ms,t04=11.43 ms,T=40.00 ms。根据被控发射波形特点,相应的SHEPWM脉冲电压如图3(b)和3(c)所示,具有半周期镜像对称性质,同时0~t01,t04~T/2+t01和T/2+t04~T阶段无脉冲电压。
由图3(b)和3(c)可见:Ud=300 V为逆变器直流侧电压;N为半个周期内的切换角总数。对于图3(b)和3(c)的脉冲,式(3)可重写如下。
1) N为奇数时,
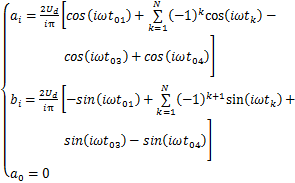 (4)
(4)
2) N为偶数时,
 (5)
(5)
式中:i=1, 3, 5, …。
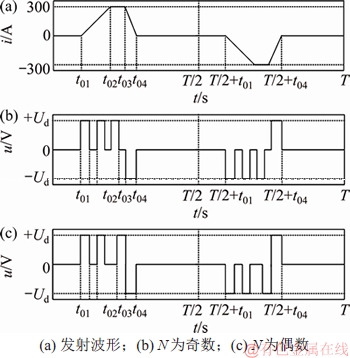
图3 HTEM发射波形半周期镜像对称阶段控制
Fig. 3 HTEM inverter output waveform under subsection control and the semi-periodic mirror symmetric
对图3(a)中发射电流进行傅里叶变换,可得发射电流的频域特性为
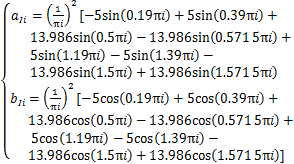 (6)
(6)
式中:i=1, 2, 3, …。
发射线圈阻感负载的频域特性为
 (7)
(7)
式中:R=0.06  ;L=1.5 mH。
;L=1.5 mH。
将式(4)~(7)代入式(2),可得HTEM半周期镜像对称SHEPWM阶段控制非线性方程组如下。
1) N为奇数时,
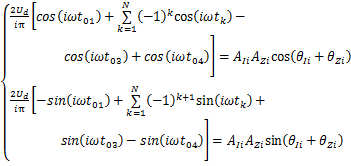 (8)
(8)
2) N为偶数时,
 (9)
(9)
式中:i=1, 3, 5, …。
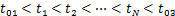 (10)
(10)
式(8)和(9)的左边是与开关角相关的多项式,右边是与发射电流及发射线圈频域特性相关的多项式。式(10)为式(8)和(9)的限定条件。因此,可以通过求解式(8)和(9),精确计算出符合发射要求的开关控制角度。
1.3 神经网络求解SHEPWM非线性方程组
SHEPWM非线性超越方程中的切换角可以通过数值迭代技术进行求解,如随机搜索方法和Newton-Raphson等,这些技术依赖于初始值的选取[13-14],若没有提供适当的初始值,则迭代求解过程不收敛。随着计算机技术的发展,科研工作者提出智能算法求解SHEPWM非线性方程组,如遗传算法[15-16]、蜂群算法[17]和神经网络算法[18]等。本文选取人工神经网络(artificial neural network, ANN)求解SHEPWM非线性方程组。与其他方法相比,该方法不依赖于初始值的选取,而且计算简单[19]。
以式(9)为例,说明利用ANN求解SHEPWM方程组的原理。将式(9)转化为如下形式:
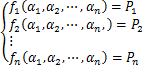 (11)
(11)
式中:fn(·)是变量(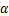 1,
1, 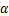 2,
2, ,
, 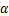 n)的函数;(
n)的函数;(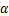 1,
1, 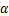 2,
2,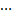 ,
, 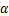 n)
n) R,R为实常数;Pn是由给定的发射电流及发射线圈频域特性得到的实常数。
R,R为实常数;Pn是由给定的发射电流及发射线圈频域特性得到的实常数。
定义式(11)的能量函数为
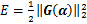 (12)
(12)
式中:
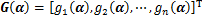 (13)
(13)
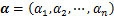 (14)
(14)
 (15)
(15)
显然,当非线性方程组式(11)的解为α*时,其能量函数式(12)的极小点也为α*。引入式(12),将解析问题转化为求解能量函数极小值的优化问题,从而可建立如下神经网络模型:
 (16)
(16)
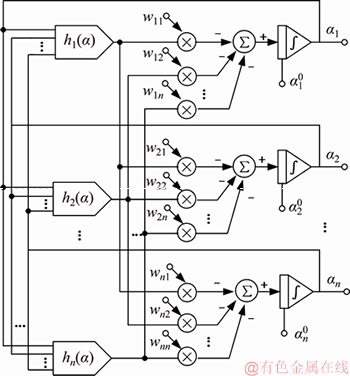
图4 式(16)的神经网络结构框图
Fig. 4 Diagram of ANN for Eq. (16)
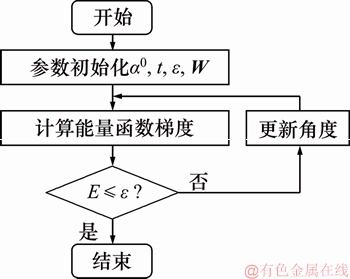
图5 神经网络求解非线性方程组流程图
Fig. 5 Flow chart of solution process with ANN
式中:W=(wij)nm是正定矩阵,通常W是对角元素均为正数的对角矩阵。E(α)为能量函数的梯度,
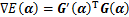 (17)
(17)
令H(α)= E(α),H(α)=(h1(α), h2(α), 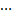 , hn(α))T,可得式(16)的单层反馈神经网络。图4所示为式(16)的神经网络结构框图。由图4可见:该神经网络有n个神经元,这些神经元通过矩阵H(α)和W相互连接。此外,在反馈结构中,α既是网络的输入向量,也是网络的输出向量。
, hn(α))T,可得式(16)的单层反馈神经网络。图4所示为式(16)的神经网络结构框图。由图4可见:该神经网络有n个神经元,这些神经元通过矩阵H(α)和W相互连接。此外,在反馈结构中,α既是网络的输入向量,也是网络的输出向量。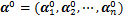 是α的初始值,在满足式(10)的条件下可任意设置。在寻找最优解时,利用循环迭代算法不断更新α,迭代规则为
是α的初始值,在满足式(10)的条件下可任意设置。在寻找最优解时,利用循环迭代算法不断更新α,迭代规则为
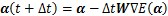 (18)
(18)
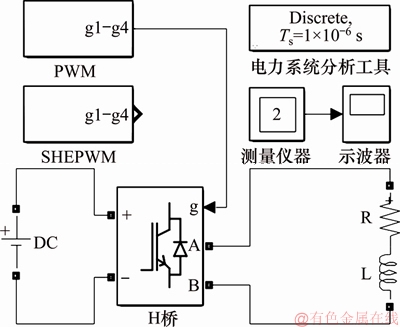
图6 HTEM发射电路仿真结构
Fig. 6 Simulation diagram of transmitting circuit
式中: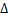 t为步长,通常为小数,如0.001。通过计算能量函数判断是否满足收敛条件。当能量函数小于或等于收敛精度时,循环结束。
t为步长,通常为小数,如0.001。通过计算能量函数判断是否满足收敛条件。当能量函数小于或等于收敛精度时,循环结束。
根据以上理论分析,给出基于ANN求解SHEPWM非线性方程组的具体步骤,如图5所示。
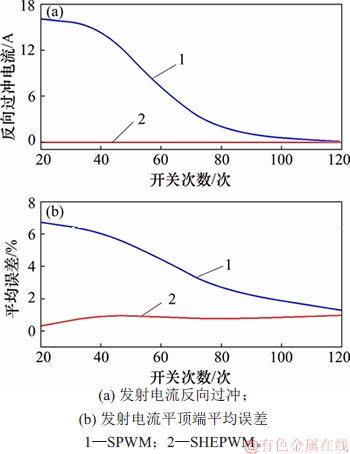
图7 2种控制策略下发射电流质量仿真对比图
Fig. 7 Simulation comparison of emission current quality under two control strategies
2 仿真结果
为了验证半周期镜像对称SHEPWM阶段控制发射方法的性能,使用MATLAB/SIMULINK研究计算机仿真。图6所示为仿真结构。由图6可见:4个IGBT组成全桥拓扑,直流侧电压为300 V。PWM及SHEPWM控制方法的开关信号分别来源于2个开关子系统,其中PWM方法的切换时刻通过被控电压波形与三角载波比较得到,SHEPWM方法的切换时间通过ANN求解式(9)得到。
在相同开关次数下,2种控制策略对发射波形的控制质量有所不同。图7所示为2种控制策略下发射电流质量仿真对比图。由图7(a)可见:随着开关次数增加,PWM方法的反向过冲逐渐减小;当周期内开关次数为120次时,反向过冲降为零。对于HTEM物探方法,发射电流的反向过冲会干扰二次场早期形成的信号,引起探测盲区。因此,在PWM方法下,为了保证反向过冲为零,要求周期内开关次数大于等于120次;而SHEPWM方法发射电流反向过冲恒为零,不受开关次数的限制。由图7(b)可见:SHEPWM方法误差维持在1%以下,不受开关次数的影响。PWM方法的误差与开关次数密切相关,随着开关次数增加,误差逐渐减小,当周期内开关次数大于等于120次时,PWM方法的误差与SHEPWM方法的误差相当,满足发射波形质量要求。
产生以上现象的原因如下:PWM方法是通过比较拟合被控波形,当开关次数过低时,拟合效果会失真。而SHEPWM方法是根据发射波形时频信息计算得到与HTEM相对应的开关时刻序列,因此,即使在较少的开关序列下,仍能实现最优的控制效果。
根据上述分析,以1个周期内开关次数分别为40和120次为例给出PWM和SHEPWM仿真结果。如图8所示为HTEM仿真结果。由图8(a)和8(b)可见:PWM控制策略的开关频率约为1.6 kHz,电压波形在1个周期内开关次数为40次,由于开关频率过低,导致电压波形在t=11.43 ms处有震荡现象,发射电流反向过冲为-15.0 A,电流平顶端平均为281.5 A。由图8(c)和8(d)可见:PWM控制策略的开关频率约为4.8 kHz,电压波形在1个周期内开关次数为120次,由于开关频率增大2倍,在 t=11.43 ms处无震荡电压,作用在发射线圈上后,电流反向过冲现象得以消除,电流平顶端平均为296.1 A。由图8(e)和8(f)可见:电压波形在1个周期内开关次数为40次,切换时刻序列如表1所示,电压波形在t=11.43 ms处降为零,电流波形无反向过冲现象,电流平顶端平均为302.8 A。图9所示为仿真电流波形局部放大图,对比分析发射电流在平顶端及下降段可得,SHEPWM(开关次数为40次)在平顶端平稳,下降沿无反向过冲,与PWM(120)发射电流质量相当,明显优于PWM(40)。仿真结果与理论分析结果相符。
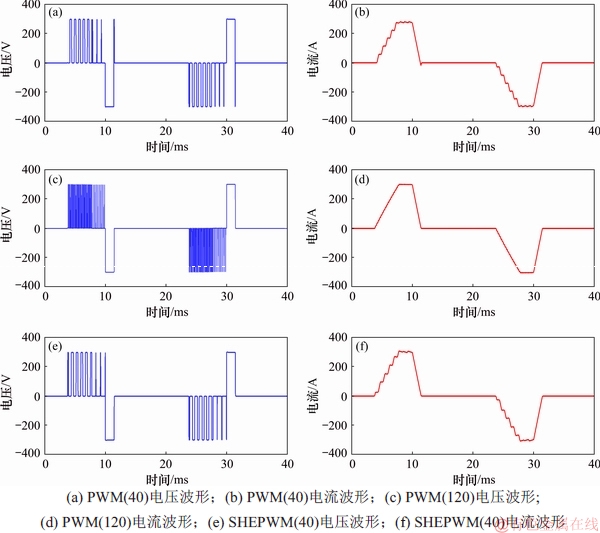
图8 HTEM仿真结果
Fig. 8 Simulation results of HTEM
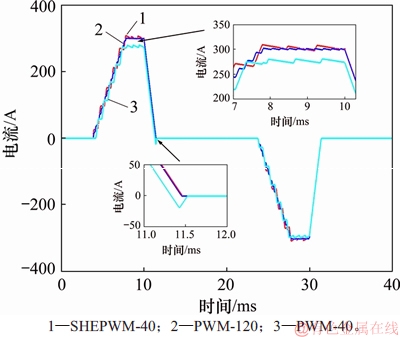
图9 仿真电流波形局部放大图
Fig. 9 Local amplification of simulated current waveform
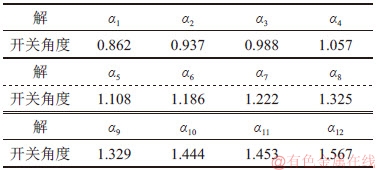
表1 式(9)的切换时刻序列
Table 1 Switching angles for Eq. (9) rad
3 实验结果
为了验证半周期镜像对称SHEPWM阶段控制发射方法的可行性,搭建了如图10所示的实验装置。实验样机主控制芯片为Altera公司FPGA EP3C25E144C8,功率变换器为三菱公司IPM-PM50B4LA060,输入直流电压为10 V,负载电阻为0.06  ,负载电感为1.5 mH。控制方法为PWM和SHEPWM,PWM控制策略的开关频率分别约为1.6 kHz和4.8 kHz,1个周期开关次数分别为40和120次,SHEPWM控制策略1个周期开关次数为40次,如表1所示。
,负载电感为1.5 mH。控制方法为PWM和SHEPWM,PWM控制策略的开关频率分别约为1.6 kHz和4.8 kHz,1个周期开关次数分别为40和120次,SHEPWM控制策略1个周期开关次数为40次,如表1所示。

图10 实验装置
Fig. 10 Experimental device
图11所示为采用Tektronix DPO3052示波器获得HTEM实验结果。由图11(a)和11(b)可见:PWM(40)控制策略的发射电流波形平顶端平均约为8 A,反向过冲约为1 A。由图11(c)和11(d)可见:PWM(120)控制策略的发射电流在平顶端平均约为10 A,无反向过冲。由图11(e)和11(f)可见:SHEPWM(40)控制策略的发射电流在平顶端平均约为10 A,无反向过冲。图12所示为实验电流波形局部放大图。由图12可见:SHEPWM(40)发射电流与PWM(120)的发射电流相当。
由于仿真是在理想环境下进行的,因此,实验结果与仿真结果略有偏差,但实验结论与仿真结论相符,验证了本文所提出的半周期镜像对称SHEPWM阶段控制方法能在低开关频率下发射高质量电流。
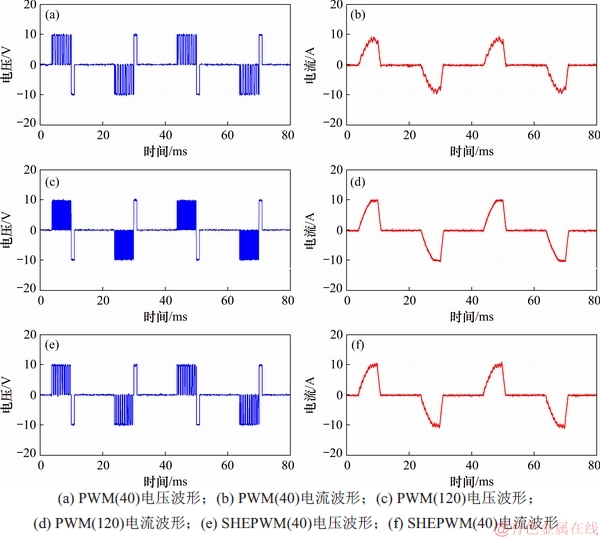
图11 HTEM实验结果
Fig. 11 Experimental results of HTEM
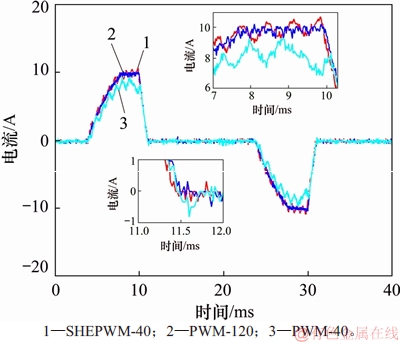
图12 实验电流波形局部放大图
Fig. 12 Local amplification of the experimental current waveform
4 结论
1) 数学模型计算结果、仿真结果和实验结果相符,验证了本文直升机时间域SHEPWM阶段控制方法的有效性。
2) 与常规的PWM控制方法相比,SHEPWM阶段控制方法在发射电流平顶段稳定性控制及发射电流反向过冲抑制方面有明显的优势,在低开关频率下,提高发射波形质量及探测精度。
参考文献:
[1] EADIE T W, PRIKHODKO A, IZARRA C. Mapping buried aquifers with HTEM in the fort McMurray, Alberta region[J]. Journal of Environmental & Engineering Geophysics, 2017, 22(1): 25-33.
[2] FOUNTAIN D. Airborne electromagnetic systems - 50 years of development[J]. Exploration Geophysics, 1998, 29(2): 1-11.
[3] RAICHE A. Modeling the time-domain response of AEM systems[J]. Exploration Geophysics, 1998, 29(2): 103-106.
[4] WITHERLY K, IRVINE R. The VTEM heli-time domain EM system-four case studies. ASEG Extended Abstracts, 2006, 2006(1): 1-4.
[5] LOKE M H, BARKER R D. Rapid least-squares inversion of apparent resistivity pseudosections by a quasi-Newton method1[J]. Geophysical Prospecting, 1996, 44(1): 131-152.
[6] PFAFFLING A, HAAS C, REID J E. Direct helicopter EM: Sea-ice thickness inversion assessed with synthetic and field data[J]. Geophysics, 2007, 72(4): F127-F137.
[7] DANIEL S. An Overview of helicopter time-domain em systems. ASEG Extended Abstracts, 2009, 2009(1): 1-6.
[8] S RENSE K I, AUKEN E. Sky TEM. a new high-resolution helicopter transient electromagnetic system[J]. Exploration Geophysics, 2004, 35(3): 194-202.
RENSE K I, AUKEN E. Sky TEM. a new high-resolution helicopter transient electromagnetic system[J]. Exploration Geophysics, 2004, 35(3): 194-202.
[9] JAMES R, JULIAN V. Footprints of airborne electromagnetic systems over one dimensional earths[J]. ASEG Extended Abstracts, 2004(1): 1-4.
[10] ZHAO Zhengming, ZHONG Yulin, GAO Hongwei, et al. Hybrid selective harmonic elimination PWM for common-mode voltage reduction in three-level neutral-point-clamped inverters for variable speed induction drives[J]. IEEE Transactions on Power Electronics, 2012, 27(3): 1152-1158.
[11] ZABALETA M, BURGUETE E, MADARIAGA D, et al. LCL grid filter design of a multi-megawatt medium-voltage converter for offshore wind turbine using SHEPWM modulation[J]. IEEE Transactions on Power Electronics, 2015, 31(3): 1993-2001.
[12] WELLS J R, NEE B M, CHAPMAN P L, et al. Selective harmonic control: A general problem formulation and selected solutions[J]. IEEE Transactions on Power Electronics, 2005, 20(6): 1337-1345.
[13] AHMADI D, ZOU KE, LI CONG, et al. A universal selective harmonic elimination method for high-power inverters[J]. IEEE Transactions on Power Electronics, 2011, 26(10): 2743-2752.
[14] SUNDARESWARAN K, CHANDRA M. Evolutionary approach for line current harmonic reduction in AC/DC converters[J]. IEEE Transactions on Industrial Electronics, 2002, 49(3): 716-719.
[15] LEE S S, CHU B, IDRIS N R N, et al. Switched-battery boost-multilevel inverter with GA optimized SHEPWM for standalone application[J]. IEEE Transactions on Industrial Electronics, 2015, Early Access(4: 1-10.
[16] MAHESWARAN D, RAJASEKAR N, PRIYA K, et al. Application of bacterial foraging algorithm and genetic algorithm for selective voltage harmonic elimination in PWM inverter[J]. Journal of Electrical Engineering and Technology, 2015, 10(3): 944-951.
[17] KAVOUSI A, VAHIDI B, SALEHI R, et al. Application of the bee algorithm for selective harmonic elimination strategy in multilevel inverters[J]. IEEE Transactions on Power Electronics, 2012, 27(4): 1689-1696.
[18] KARUVELAM P S, RAJARAM M. Real time implementation of SHE PWM in single phase matrix converter using linearization method[J]. Journal of Electrical Engineering and Technology, 2015, 10(4): 1682-1691.
[19] BALASUBRAMONIAN M, RAJAMANI V. Design and real-time implementation of SHEPWM in single-phase inverter using generalized hopfield neural network[J]. IEEE Transactions on Industrial Electronics, 2014, 61(11): 6327-6336.
(编辑 秦明阳)
收稿日期: 2019 -03 -18; 修回日期: 2019 -06 -20
基金项目(Foundation item):国家重点研发计划项目(2017YFC0601802) (Project(2017YFC0601802) supported by the National Key Research and Development Program of China)
通信作者:陈楠,博士,从事电力变换与电磁兼容研究;E-mail:chennan16@mails.jlu.edu.cn