


Trans. Nonferrous Met. Soc. China 22(2012) 411-418
Optimization of AZ80 magnesium alloy squeeze cast process parameters using morphological matrix
GUO Zhi-hong1, HOU Hua1, ZHAO Yu-hong1, QU Shu-wei2
1. School of Materials Science and Engineering, North University of China, Taiyuan 030051, China;
2. School of Mechanical Engineering and Automation, North University of China, Taiyuan 030051, China
Received 4 June 2010; accepted 30 August 2011
Abstract: The squeeze cast process parameters of AZ80 magnesium alloy were optimized by morphological matrix. Experiments were conducted by varying squeeze pressure, die pre-heat temperature and pressure duration using L9(33) orthogonal array of Taguchi method. In Taguchi method, a 3-level orthogonal array was used to determine the signal/noise ratio. Analysis of variance was used to determine the most significant process parameters affecting the mechanical properties. Mechanical properties such as ultimate tensile strength, elongation and hardness of the components were ascertained using multi variable linear regression analysis. Optimal squeeze cast process parameters were obtained.
Key words: AZ80 magnesium alloy; squeeze cast; process parameters; morphological matrix; optimization
1 Introduction
Squeeze casting (SC) is a general term to specify a fabrication technique where liquid metal is fed into a permanent die and pressure is applied via a hydraulic ram until solidification is complete [1]. It has a number of advantages over sand-casting and gravity die casting. Squeeze forming process is a special casting technique that combines the advantages of traditional high pressure die casting, gravity permanent mold die casting and common forging technology. It is a relatively new casting process and otherwise called squeeze forming, liquid forging, liquid pressing, extrusion casting, liquid metal stamping, pressure crystallization and corthias casting. The process is first discovered by the Russians and later develops in USA, Europe and Japan. This advanced casting method is applied to the processing of ferrous and non-ferrous materials besides composites. The microstructural refinement of squeeze cast products is desirable in many critical applications. This process is simple, economical and it can be automated easily [2].
SC is a hybrid metal forming process, in which the molten metal solidifies under pressure within the die cavity. The applied pressure forces the molten metal to have an intimate contact with the mould metal which in turn leads to rapid heat transfer that yields pore-free and fine grains [3-10], and close dendrite arm spacing components with mechanical properties approaching those of a wrought product. The most important parameters in SC have been identified as melt temperature, melt quality (i.e., the absence of oxide films and inclusions) and quantity, die temperature, applied pressure and pressure duration [11].
The aerospace and the automobile sectors have been the main driving force behind the SC process using light metals to obtain components with improved mechanical properties. The majority of investigations to assess the effect of SC process parameters have considered magnesium alloys and their composites. Among the magnesium-based alloys, AZ80 (8.4% Al, 0.48% Zn, 0.02% Mn, 0.0026% Cu, 0.0006% Ni, 0.0014% Fe, 0.026% Si, 0.0007% Be and Mg balance, mass fraction) is preferred to obtain components with good mechanical properties. The magnesium alloy AZ80 is associated with excellent pressure tightness, good hot tear resistance, good ductility, good weldability, good machinability and high corrosion resistance [12-13]. The SC process parameters such as squeeze pressure, die pre-heat temperature and pressure duration have been considered to optimize the ultimate tensile strength (UTS), elongation and hardness.
Design optimization is the process to find the maximum/minimum of the parameters called the objective function and it must satisfy a certain set of specified requirements within constraints. In multi-objective optimization, all the components of vectors which store the different objectives should be optimized simultaneously [14].
Morphology is a method of thinking introduced by the astrophysicist ZWICKY [15]. One of the ideas of morphology is to systematically search for a solution to a problem by trying out all possible combinations in a matrix. ZWICKY named the matrix a “morphologic box”, but it is also known as a morphological matrix or morphological chart. The fact that the search also reveals unorthodox combinations is one of the basic ingredients of creativity, which is also similar to the theory of inventive problem solving.
The morphological matrix is created by decomposing the main functions of the product into sub-functions which are listed on the vertical axis of the matrix. Possible solution principles for each function are then listed on the horizontal axis. Different concepts are created by combining various solution principles to form a complete system concept [15].
ZWICKY did not use the words function and solution but called both function and solution as parameters. In this work, sub-systems on the vertical axes were used instead of functions. However, the basic principle of the morphological matrix stays the same to span all possible solutions to a problem.
The optimization methodology adopted in this work was a morphological approach. Morphological matrix (MM) efficiently exploited useful information to generate new solutions with better performance.
2 Experimental
AZ80 alloy was used as the casting material and its pouring temperature was maintained at 750 °C. The molten metal in the die was subjected to pressure after pouring and the pressure duration varied from 15 to 45 s. The cylindrical squeeze castings (d 40 mm×200 mm) with high height-to- thickness ratio were obtained finally.
A 40 t universal testing machine was employed for the application of pressure and the applied pressure level varied from 40 to 110 MPa. H13 die steel was used as the die material, and the die cavity was coated by graphite. The die set-up was fitted on the hydraulic table of the universal testing machine by base plate. The punch was fitted in the middle crosshead of the universal testing machine for the application of pressure, whereas the ejector was used to enable the removal of castings. The ceramic electrical heater was used to preheat the die and the castings, followed by pre-heating of the die at 160 and 320 °C, respectively. The photos of experimental set-up are shown in Fig. 1.
It was observed that a squeeze pressure below 40 MPa did not considerably improve the mechanical properties and the die was designed to withstand a maximum squeeze pressure of 110 MPa. Hence, the bound for squeeze pressure was set as 40 MPa≤p≤110 MPa. The die pre-heat temperature varied from ambient temperature and up to a maximum temperature of 320 °C. If the die was heated above this temperature, it was found that increasing solidification time led to the loss of production. Hence, the bound for die pre-heat temperature θ was set as 35 °C≤θ≤320 °C. It was found experimentally that the minimum time required for complete solidification of casting was 15 s and it was not expected to go beyond 45 s due to any change under operating conditions. Hence, the pressure duration bound t was fixed as 15 s≤t≤45 s.

Fig. 1 Photos of experimental set-up: (a) Upper die; (b) Lower die; (c) Overall die
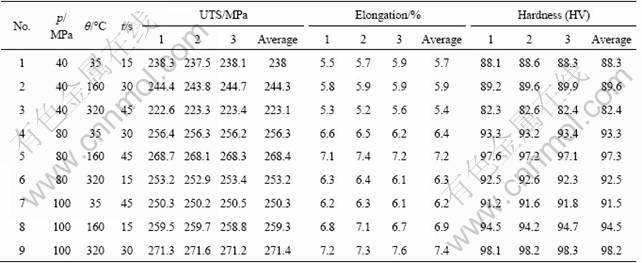
Taguchi method is one of the efficient problem solving tools to upgrade the performance of products and processes with a significant reduction in cost and time involved [16]. By opting Taguchi method, the number of experiments to be conducted was reduced to 9, instead of the actual 21 experiments for the above chosen 3 parameters with 3 levels in this work. The experiments were conducted as per trial data sheet of L9 (33) orthogonal array. The castings were made under different conditions and the tensile strength, elongation and hardness values along with the average response values were ascertained.
3 Results and discussion
3.1 Development of mathematical model
The squeeze cast process parameters, namely pressure, die preheating temperature and pressure duration at 3 levels are considered in this work and the details are presented in Table 1. Selection of an appropriate orthogonal array based on the chosen process parameters is the prime aim in the Taguchi method. The total degrees of freedom for 3 parameters in each of the 3 levels are 6. Then, a 3-level orthogonal array (L9 33) with 9 experimental runs (degree of freedom = 9 - 1 = 8) is selected for the present research. Orthogonal array (OA) is the shortest possible matrix of combinations in which all the parameters vary at the same time and their effect and performance interactions are studied simultaneously.
The name of an array indicates the number of rows and columns, and also the number of levels in each of the columns. Thus, the array L9 33 has 9 rows and 3 columns of 3 levels. The array is based upon the theory of orthogonality. It states that each and every level of each and every parameter is in combination with each and every level of every other parameter at least once [17]. A well designed experiment can reduce substantially the number of experiments required [18]. With the selection of (L9 33) orthogonal array, using 3 parameters and 3 levels for each, the number of experiments required can be drastically reduced to 9, which in classical combination method using full factorial experimentation would require 33=27 experiments to capture the influencing parameters. The SC process parameters, namely squeeze pressure (A), die preheating temperature (B) and pressure duration (C) are assigned to the first, second and third columns of (L9 33) array, respectively.
3.2 Analysis of results
After the collection, the data are analyzed by calculating signal/noise (S/N) ratio. The S/N ratio is simply a quality indicator by which the effect of changing a particular process parameter on the performance of the process or product is evaluated. In general, a better signal is obtained when the noise is smaller, so that a larger S/N ratio yields better final results. This means that the divergence of the final results becomes smaller. The S/N ratio (η) of each experimental run is calculated based on the following equation and the values are listed in Table 2.
Table 1 Results of (L933) orthogonal array experiments
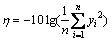
where n is the number of measurements in a trial (here n=3) and yi is the ith measured value in a row.
After the collection of raw data, average effect response values are calculated based on the following procedure. Typically, the average effect for level 1 of the squeeze pressure is computed using the data from No. 1-3 in Table 2. Similarly, the average effects for levels 2 and 3 of squeeze pressure were computed using data from No. 4-6 and 7-9 in Table 2, respectively. The average effects of die preheating temperature and pressure duration are computed for all the levels as illustrated above and listed in Table 3. The average effect responses for S/N ratios for each level of process parameters are summarized in Table 4.
Pareto ANOVA computation is done for the quality characteristics of ultimate tensile strength, elongation and hardness to study the contribution ratio of the process parameters as listed in Table 5. The Pareto analysis shows that squeeze pressure has a larger impact suggests that the optimum level of process parameters as on the ultimate tensile strength, elongation and hardness, as shown in Fig. 2. Further, Pareto ANOVA calculation squeeze pressure of 100 MPa, die preheating temperature of 160 °C and pressure duration of 30 s are the proposed levels to improve the ultimate tensile strength, elongation and the hardness.
Table 2 Computation of S/N ratio for ultimate tensile strength, elongation and hardness
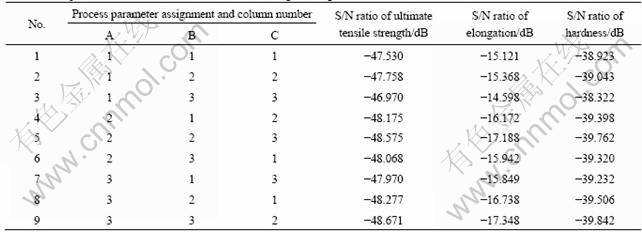
Table 3 Average effect response for raw data
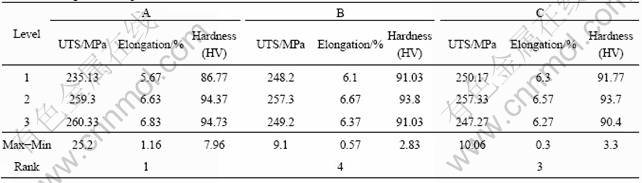
Table 4 Average effect response for S/N ratio
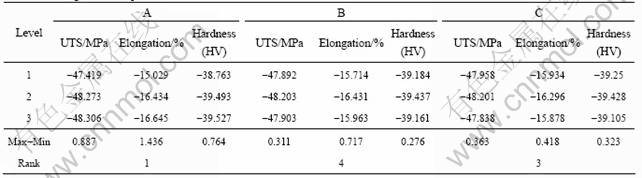
Table 5 Computation of Pareto ANOVA for surface ultimate tensile strength and hardness
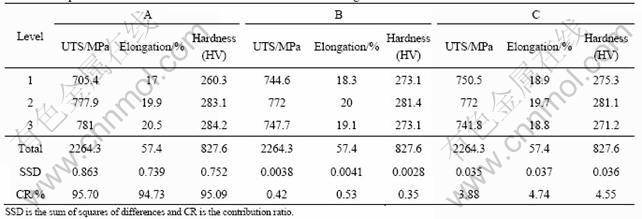
3.3 Response graphs and morphological matrix
The response graphs exhibit a pictorial view of variation of each parameter and describe the effect on the system performance when a parameter shifts from one level to another. Figures 3(a) and (b) show the response for two parameters, namely squeeze pressure and die preheating temperature. Figures 4(a) and (b) show the response for S/N ratio, as an example, level 3 for squeeze pressure (100 MPa, see No. 7-9 in Table 2) has the highest S/N ratio value, which indicates that the casting performance at such level produces the minimum variation of the ultimate tensile strength, elongation and hardness.
There are many types of crossover operators like edge recombination crossover and partially mapped crossover, ordered crossover, simulated binary crossover. In this work, edge recombination crossover is used. This type of crossover results in faster convergence of optimal solution.
The test runs are carried out on MM by varying different MM input parameters. After several test runs, the following final MM input parameters are found to give better solution.
The steady increase in ultimate tensile strength, elongation and hardness of the best solution in each generation to a best possible value can be attributed to the selection procedure used, namely roulette wheel selection. Final optimized AZ80 SC process parameters are given as squeeze pressure 100 MPa, die temperature 160 °C and pressure duration 30 s.
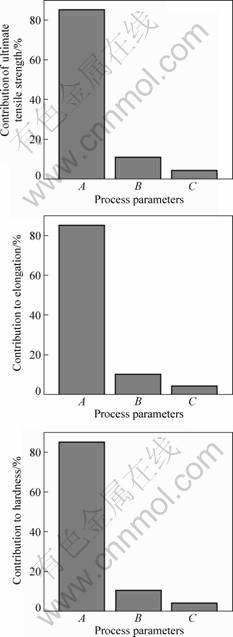
Fig. 2 Pareto diagrams of contribution of ultimate tensile strength (a), elongation (b) and hardness (c)
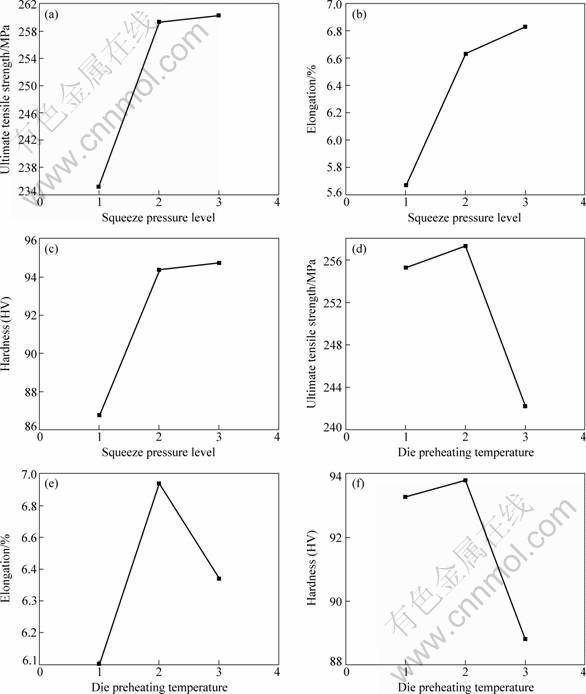
Fig. 3 Response of squeeze pressure (a-c) and die preheating temperature (d-f) levels to ultimate tensile strength (a, d), elongation (b, e), hardness (c, f)
4 Conclusions
1) The application of MM is aimed at the maximization of mechanical properties of the SC components and the developed morphological matrix successfully searches the maximum possible ultimate tensile strength and hardness values and the input process parameters that can yield those specific values.
2) The proposed MM approach is efficient and gives promising results. The heuristic is also found to give better solutions in shorter experimental time. In this method, edge recombination crossover is used and gives better results.
3) Squeeze pressure has a larger impact on the ultimate tensile strength, elongation and hardness of the AZ80 alloy. The optimized AZ80 SC process parameters is squeeze pressure of 100 MPa, die temperature of 160 °C, pressure duration 30 s.
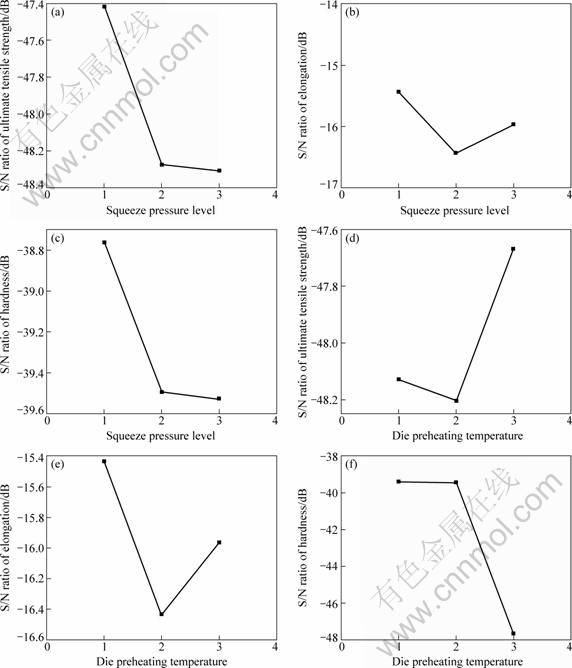
Fig. 4 Response of S/N ratio of squeeze pressure (a-c) and die preheating temperature (d-f) levels to ultimate tensile strength (a, d), elongation (b, e), hardness (c, f)
References
[1] CHADWICK G A, YUE T M. Principles and applications of squeeze castings [J]. Met Mater Int, 1989, 5(1): 6-12.
[2] VIJAYARAM T R, SULAIMAN S, HAMOUDA A M S, AHMAD M H M. Fabrication of fiber reinforced metal matrix composites by squeeze casting technology [J]. J Mater Process Technol, 2006, 178(14): 34-38.
[3] CHEN Guo-qin, XIU Zi-yang, MENG Song-he, WU Gao-hui, ZHU De-zhi. Thermal expansion and mechanical properties of high reinforcement content SiCp/Cu composites fabricated by squeeze casting technology [J]. Transactions of Nonferrous Metals Society of China, 2009, 19(S1): s600-s604.
[4] ZHANG Ke-wu, ZHAO Hai-dong, OUYANG Xiao-xian, ZHANG Wei-wen, LI Yuan-yuan. Microstructures and mechanical properties of Al-Si-Cu-T4 solidified at different squeeze pressures [J]. The Chinese Journal of Nonferrous Metals, 2009, 19(4): 625-632. (in Chinese)
[5] LI Run-xia, LI Rong-de, BAI Yan-hua, QU Ying-dong, YUAN Xiao-guang. Effect of specific pressure on microstructure and mechanical properties of squeeze casting ZA27 alloy [J]. Transactions of Nonferrous Metals Society of China, 2010, 20(s1): s59-s63.
[6] ZHANG Ming, ZHANG Wei-wen, ZHAO Hai-dong, ZHANG Da-tong, LI Yuan-yuan. Effect of pressure on microstructures and mechanical properties of Al-Cu-based alloy prepared by squeeze casting [J]. Transactions of Nonferrous Metals Society of China, 2007, 17(3): 496-501.
[7] WU Gao-hui, CHEN Guo-qin, ZHU De-zhi, ZHANG Qiang, JIANG Long-tao. Effect of particle size on thermo-physical properties of SiCp/Cu composites fabricated by squeeze casting [J]. Transactions of Nonferrous Metals Society of China, 2005, 15(2): 217-220.
[8] HU Mao-liang, ZHAO Mi, JI Ze-sheng, SUN Guang-bin, PIAO Yong-ji. Effect of squeezing casting technology on structures and properties of air-conditioner swaying tray of automobile [J]. The Chinese Journal of Nonferrous Metals, 2006, 16(3): 400-405. (in Chinese)
[9] SUKUMARAN K, RAVIKUMAR K K, PILLAI S G K. Studies on squeeze casting of Al2124 alloy and 2124-10%SiCp metal matrix composite [J]. Mater Sci Eng A, 2008, 490(1-2): 235-241.
[10] LEE K H, KWON Y N, LEE S H. Effects of eutectic silicon particles on tensile properties and fracture toughness of A356 aluminum alloys fabricated by low-pressure-casting, casting-forging, and squeeze-casting processes [J]. Journal of Alloys and Compounds, 2008, 461(1-2): 532-541.
[11] CHADWICK G A, STUBBINGTON C A. High quality squeeze casting of monolithic and reinforced aluminium alloys [J]. Foundryman 1991, 84 (12): 471-474.
[12] YONG M S, CLEGG A J. Process optimization for a squeeze cast magnesium alloy [J]. J Mater Process Technol, 2004, 145(1): 134-141.
[13] YONG M S, CLEGG A J. Evaluation of squeeze cast magnesium alloy and composite [J]. Foundryman, 1998, 92(3): 71-75.
[14] ANDRESTORO B, GIRONSIERRA J M. Multi objective optimization and multivariable control of the beer fermentation process with the use of evolutionary algorithms [J]. J Zhejiang Univ Sci, 2003, 5(4): 378-389.
[15] OLVANDER J, LUNDEN B, GAVEL H. A computerized optimization framework for the morphological matrix applied to aircraft conceptual design [J]. J Computer-Aided Design, 2009, 41(3): 187-196.
[16] TSAO C C, HOCHENG H. Taguchi analysis of delamination associated with various drill bits in drilling of composite material [J]. Int J Mach Tools Manuf, 2004, 44(10): 1085-1090.
[17] GANDHI A. Problem solving using Taguchi DOE techniques [J]. Indus Eng J, 2003, 32 (4): 16-25.
[18] ALAUDDIN M, BARADIE M E, HASHMI M S J. Computer aided analysis of a surface roughness model for end milling [J]. J Mater Process Technol, 1995, 55(2): 123-127.
AZ80镁合金挤压铸造工艺参数的形态学矩阵优化
郭志宏1,侯 华1,赵宇宏1,屈淑维2
1. 中北大学 材料科学与工程学院,太原 030051;
2. 中北大学 机械工程与自动化学院,太原 030051
摘 要:运用形态学矩阵对AZ80镁合金挤压铸造工艺参数进行优化。采用L9(33)田口方法中的正交列对不同挤压压力、模具预热温度和压力持续时间进行组合。采用一个3水平正交阵列确定信噪比,通过方差分析确定影响力学性能最重要的工艺参数,并利用多变量线性回归分析确定拉伸强度、伸长率和硬度,获得了最佳的挤压铸造工艺参数。
关键词:AZ80镁合金;挤压铸造;工艺参数;形态学矩阵;优化
(Edited by FANG Jing-hua)
Foundation item: Project (50975263) supported by the National Natural Science Foundation of China; Project (2011DFA50520) supported by International Science Technology Cooperation Program of China
Corresponding author: HOU Hua; Tel: +86-351-3557118; E-mail: houhua@263.net
DOI: 10.1016/S1003-6326(11)61192-8