DOI： 10.11817/j.issn.1672-7207.2020.12.014
基于三质点模型的仿人机器人节能步行
何杰，张晓晖，肖晓晖，丁加涛
(武汉大学 动力与机械学院，湖北 武汉，430072)
摘要：为了实现高能效的双足步行，提出基于三质点线性倒立摆模型(3MLIPM)的步态生成与优化策略。首先，定义表征单位能耗的步态周期(UEWC)，利用三质点模型，对机器人进行运动学建模与步行能耗评估，建立机器人步行过程的能耗评价模型，分析各质量块的运动性质，提出基于质心(CoM)加速度优化的二次型步行能耗评价指标；其次，对3MLIPM进行动力学建模，将CoM运动分为稳定分量与不稳定分量，CoM最优轨迹求解转化为求解运动分量误差项，通过跟踪参考的零力矩点(ZMP)轨迹，利用无约束优化算法求解对应的能耗最低的CoM轨迹；最后，实现了步态的在线生成，并且为消除腿部质量摆动导致的躯干质心附加运动，通过二分搜索的修正算法，修正3MLIPM的步行参数输入(步长和步宽)，进一步降低了双足步行的能量消耗。通过仿真和试验验证了算法的可行性和有效性。研究结果表明：提出的能耗评价指标能够表征三质点步行系统的真实能耗，并且能够用于指导最优CoM轨迹生成；利用双足稳定支撑域，可以优化参考ZMP轨迹以实现低能耗步行；通过修正三质点模型的名义步行参数输入，消除等效ZMP产生的附加运动，针对不同形式ZMP参考轨迹，修正后的三质点模型相比于传统单质点模型，可以有效降低步行能耗。
关键词：三质点线性倒立摆模型(3MLIPM)；零力矩点(ZMP)；能量效率；双足步行；仿人机器人
中图分类号：TP242 文献标志码：A 开放科学(资源服务)标识码(OSID)
文章编号：1672-7207（2020）12-3396-11
Energy-efficient bipedal walking for humanoid robots based on a three-mass model
HE Jie, ZHANG Xiaohui, XIAO Xiaohui, DING Jiatao
(School of Power and Mechanical Engineering, Wuhan University, Wuhan 430072, China)
Abstract: With the aim of realizing the energy-efficient bipedal walking, a novel strategy was proposed for gait generation and optimization based on the three-mass linear inverted pendulum model(3MLIPM). Firstly, walking cycle of unit energy cost(UEWC) was defined, and the mathematical model for evaluating the energy cost of humanoid robots during the walking process was derived by exploiting the three-mass model. After analyzing the motion property of each lumped mass, the quadratic evaluation index was proposed based on the optimization of the acceleration of center of mass(CoM). Secondly, the dynamic model of the 3MLIPM was built to decompose the motion of CoM into stable component and unstable component. Therefore, the solution of the CoM optimal trajectory was transformed into the solution of the motion component error term. By tracking the reference zero moment point(ZMP) trajectory, the corresponding CoM trajectory of the minimal energy consumption was solved by an unconstrained optimization algorithm. Finally, the walking pattern was generated online. To eliminate additional movement of torso CoM caused by the mass swing of the legs, the nominal step parameters, including step length and step width, were modified by modifying binary search algorithm. Therefore, the energy cost would be reduced to a further degree. The feasibility and effectiveness of the proposed method were demonstrated by simulation and experiment results. The results show that the proposed evaluation index can characterize the actual energy consumption of the three-mass walking system and can be used to guide the optimal CoM trajectory generation. Besides, by utilizing the allowable support region, reference ZMP trajectories can be optimized to realize energy-efficient walking. Furthermore, through modifying the nominal step parameters inputs of the 3MLIPM, additional motion generated by equivalent ZMP is eliminated. Compared with traditional single-mass model, the modified three-mass model can effectively reduce walking energy consumption for different forms of ZMP reference trajectories.
Key words: three-mass linear inverted pendulum model(3MLIPM); zero moment point(ZMP); energy efficiency; bipedal walking; humanoid robot
仿人机器人具有人类的外观特征以及良好的环境适应性，在家庭服务、抢险救灾和野外探测等领域有着广阔的应用前景。近年来，国内外在仿人机器人样机研制[1]、步态规划[2-3]和步行控制[4-5]等方面取得了一定的研究成果。但是，为满足实际应用需求，需进一步降低步行过程中的能量消耗。被动步行和欠驱动机器人在节能行走方面有一定的优势[6-7]，但是被动步行的地形适应能力差，只能实现下坡或者平地行走；而欠驱动步行机器人需要特殊的结构设计并依赖复杂的步行控制策略。为此，本文针对全驱动机器人，研究低能耗的步态生成与优化策略。给定目标行走距离，传统的能耗优化方法首先使用能耗评价函数估算初始步行参数(包括步长、步宽等)下所需能耗，然后，沿着降低系统总能耗的梯度方向更新步行参数以实现节能行走。事实上，总步行能耗取决于每个步行周期的单位能耗(unit energy cost，UEC)[8]。
为评估UEC，首先需要提出能耗评价指标。一般来说，可使用机器人的关节功率作为UEC能耗评价函数。为计算关节功率，ZHANG等[9-10]首先规划出步态(包括质心(center of mass，CoM)轨迹和摆动腿轨迹)，然后，从理论上分析期望的关节角速度和力矩。但是，该方法需要进行逆运动学迭代，耗时较长。SHIN等[11]建立电机电压和电流与关节角度之间的关系模型来估计UEC，但是，建模过程比较繁杂。此外，关节功率本身难以直接指导机器人CoM轨迹的生成。因此，一些研究者[12]利用动力学简化模型，把集中质量块运动所需要的能量作为系统能耗。例如，基于线性倒立摆模型(linear inverted pendulum model，LIPM)，BRANDAO等[13]把集中质点跟踪目标CoM轨迹所需要的能耗当做UEC，从而实现能耗优化，但是，该工作并没有建立CoM运动与UEC之间的数学模型。针对步态生成，首先需要保证步行稳定性。最常用且有效的做法是保证零力矩点(zero moment point，ZMP)始终在足部支撑多边形内部[14]。仿生学研究表明，人类在步行过程中能通过移动ZMP位置(在双足支撑域内)降低能耗[10]。基于此，研究者们提出不同形式的参考ZMP轨迹以实现高效行走。SHIN等[11]在单足支撑相(single support phase，SSP)使用零ZMP位移并限定双足相(double support phase，DSP)期间CoM加速度为零，最终通过优化可行域内的ZMP运动获得较低能耗。此外，ERBATUR等[15-16]等使用了直线形和三角函数形的ZMP参考轨迹。虽然以上工作都提高了能量效率，但是并没能解释利用ZMP移动能够降低能耗的机理。在之前的工作中，针对LIPM模型，建模分析步行能耗，提出了以质心加速度最小化为目标的能耗评价函数。在此基础上证明了合理规划参考ZMP轨迹能有效降低步行能耗。但是以上工作都是基于单质点模型，存在较大的模型误差。当腿部质量比较大时，可能导致步态失稳。由于未能考虑躯干质量的运动，容易导致较大的关节力矩并降低能量效率。为平衡计算复杂度和模型精度，研究者提出了三质点线性倒立摆模型(three-mass linear inverted pendulum model，3MLIPM)[17-18]。虽然文献[19]利用该模型研究了能耗规律，但与文献[11]的研究类似，该工作同样没能充分利用双足支撑域。
因此，本文基于3MLIPM，研究高能效步态的生成与优化。首先，研究3MLIPM下机器人步行能耗模型，提出适合三质点模型的能耗评价指标；然后，引入等效ZMP和等效自然频率的概念，利用无约束控制方法实现最优CoM轨迹的生成，比较不同形式的参考ZMP轨迹对应的单位能耗，揭示ZMP运动与能耗之间的关系；最后，修正步态参数输入，进一步降低使用3MLIPM时双足步行的能量消耗。
1 双足步行能耗建模
1.1 单位能耗步行周期-UEWC
为便于分析行走过程中的能量消耗，定义表征单位能耗的步态周期(walking cycle of unit energy cost，UEWC)，如图1所示。该周期由前半单足支撑相(pre-half SSP，SSPpre)，过渡双足支撑相(transitional DSP, DSPtr)和后半单足支撑相(post-half SSP，SSPpost)组成。
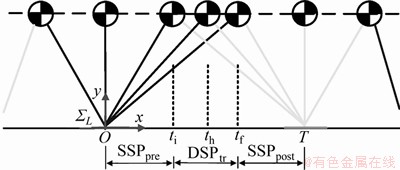
图1 单位能耗步行周期
Fig. 1 Definition of UEWC
由图1可见：SSPpre从倒立摆中心经过当前支撑腿正上方位置开始，一直持续到摆动腿落地；DSPtr为双足支撑阶段；SSPpost从下一摆动腿离地开始，直到倒立摆中心运动到下一支撑腿正上方位置。
在重力和地面反力作用下，不考虑踝关节力矩输入，可以推断：在SSPpre阶段，倒立摆中心做加速运动；在SSPpost阶段，倒立摆中心做减速运动。同时，不难控制倒立摆中心在DSPtr前半段加速而在后半段减速。因此，相对于局部坐标(图1中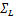
所示)，可以得到
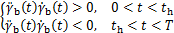(1)
式中：
为时间；th为半周期时刻；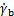
和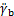
分别为倒立摆中心沿x轴或y轴的水平速度和加速度；
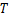为单个周期时间。
1.2 3MLIPM运动学建模
LIPM假设机器人全部质量集中在质心[12]。虽然有利于简化计算，但是该模型不能反映实际质量分布对双足步行的影响。而3MLIPM假设3个分布于躯干、左腿和右腿的集中质量块[17-18]。双足步行三质点线性倒立摆模型如图2所示。图2中，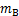
，
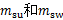分别表示躯干、支撑腿和摆动腿的质量。
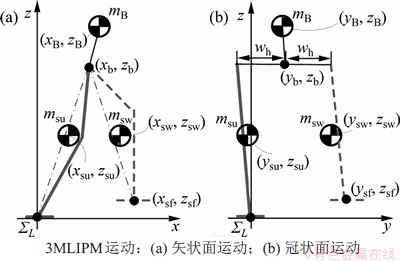
图2 双足步行三质点线性倒立摆模型
Fig. 2 3MLIPM for bipedal walking
考虑机器人实际结构的质心偏移，可计算三质心位置如下(以SSPpre阶段运动右腿支撑为例)：
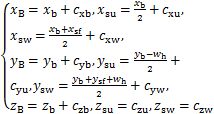(2)
式中：
，
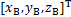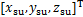和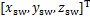
分别为躯干、支撑腿和摆动腿质心位置；
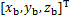和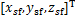
分别为髋部中心位置和摆动足位置；
，
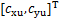和
分别为躯干、支撑腿和摆动腿质心水平偏移量；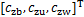
分别为躯干高度偏移量、支撑腿质心高度和摆动腿质心高度(3MLIPM中假设各质量块的质心高度为恒定值)；wh为髋关节到髋部中心的侧向水平距离。
从式(2)可见：在SSPpre阶段，躯干和支撑腿质心运动只取决于髋部中心运动，摆动腿质心运动由髋部中心运动和摆动足部运动共同决定。此外，在SSPpost阶段，也能得出同样地结论。在DSPtr阶段，三质点运动都只由髋部中心运动来决定。为简化篇幅，这里不进行详细推导。
1.3 3MPLIPM下步行能耗评估
由于3MLIPM假设各质点高度恒定，在不考虑地面摩擦导致额外能耗的情况下，步行过程中的能耗为推动3个质量块跟踪期望的水平CoM轨迹所需要的能量输入。因此，UEC的名义表达式如下：
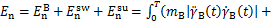
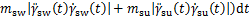(3)
式中：
为运动总耗能；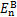
，
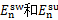分别为躯干、摆动腿和支撑腿质心运动消耗的能量，
，
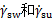分别为躯干、摆动腿和支撑腿质心水平速度，
，
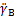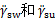分别为躯干、摆动腿和支撑腿质心水平加速度。
1.3.1 躯干质量块名义单位能耗
假定水平质心偏移量为恒定值的情况下，结合式(1)~(3)，得出：
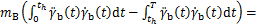
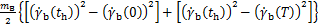(4)
由于机器人上半身质量一般远大于各腿部质量，可以把髋部中心等效为上一节中倒立摆中心。由于倒立摆中心在[0，th]一直加速而在[th，T]一直减速，可作出如下推断：
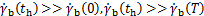(5)
由此，式(4)可以进一步简化为
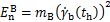(6)
因此，使得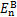取最小值的条件是中间时刻髋部中心(倒立摆中心)速度最小。结合式(1)中的运动性质，可推断出需要倒立摆中心在整个周期内加速度最小。因此，本文提出如下能耗最优指标：
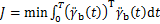(7)
式中：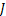
为单位周期内的最优能耗指标。
1.3.2 支撑腿质量块名义单位能耗
以在UEWC的初始时刻由左腿支撑为例，由图1的定义可知，在SSPpost期间，左腿将变成摆动腿而右腿将转变为支撑腿。该部分所指的摆动腿质量块，是从所处的运动阶段来考虑的，并不是针对左腿或者右腿。由1.2节的分析可知，支撑腿质心的运动只由髋部中心的运动决定。因此，在1个UEWC内，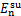
只取决于髋部中心运动：
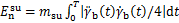
(8)
同样，式(7)是使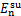取最小值的条件。
1.3.3 摆动腿质量块名义单位能耗
同支撑腿一样，本文从运动状态的角度定义摆动腿(跟左腿还是右腿无关)。以在UEWC的初始时刻由左腿支撑为例，在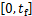
时间段内，右腿为摆动腿；在
时间段内，左腿为摆动腿。但无论是左腿还是右腿，摆动腿质心的运动都由式(2)决定，即由躯干中心和摆动足部的运动共同决定。其中，在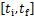
内，摆动腿质心的运动方程的中
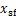和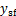
都为固定值，此时，摆动腿质心的速度和加速度都只由躯干中心的速度和加速度决定。
因此，针对摆动腿质量块，结合式(2)，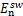
由下式决定：
(9)
式中：
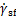和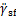
分别为摆动足水平速度和加速度。
在冠状面内无侧偏行走时，摆动足侧向速度和加速度都为0。因此，冠状面运动需要的能耗只取决于倒立摆中心运动，能耗最优指标已经由式(7)给出。
在矢状面内，根据图1定义，以向前行进为例，摆动足运动满足如下约束：
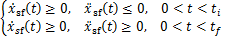(10)
同时，受冠状面运动的启发，要想获得较小的能耗，期望摆动足前向加速度为尽可能小。本文近似为0。由此，式(9)可以近似为：
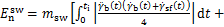
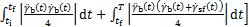(11)
考虑前向运动过程中，髋部中心和摆动足速度一直不小于0。因此，式(11)取得最小值的必要条件是髋部中心加速度最小，即式(7)。
最终，本文以髋部中心全局加速度平方和最小作为能耗最优指标，即式(7)。虽然推导过程经过大量简化，但是该目标函数只是用做能耗评估而不是能耗精确计算，所以，这些简化是可以接受的。
2 质心轨迹优化
给定步行参数，如步长、步宽和迈步周期等，摆动足轨迹可以由多项式插值得出。为生成节能步态，该部分集中在CoM轨迹的生成。为保证步行稳定性，ZMP轨迹应保持在在双足支撑区域以内，如图3所示。
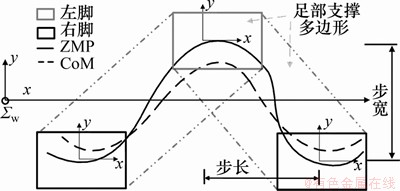
图3 双足步行足部支撑多边形
Fig. 3 Foot support polygon of bipedal walking
由此，问题转化为：给定参考ZMP轨迹，求解最优的CoM轨迹以获得最小的单位能耗。
2.1 3MLIPM动力学建模
使用3MLIPM模型，ZMP位移计算如下：
(12)
式中：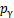
为ZMP位移；
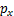和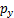
分别为沿x轴(向前为正)和沿y轴(向左为正)的ZMP位置；
，
，
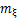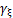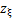和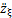
分别为三质点的质量、质心水平位置、竖直高度和竖直方向加速度；g为重力加速度。
因此，给定参考ZMP轨迹和摆动足轨迹，倒立摆中心轨迹可以由式(2)和式(12)决定。由于线性倒立摆模型中假定固定的高度，式(12)可以整理为
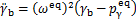(13)
式中：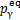
为等效ZMP轨迹，
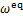为等效自然频率，计算如下：
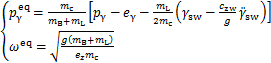(14)
式中：mL为腿部质量(mL=msu=msw)；mc为机器人总质量(mc=mB+msu+msw)；ex，ey和ez计算如下：
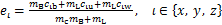(15)
如果假设msu=msw=0，式(13)~(15)的结果将与文献[12]计算结果一致。
2.2 质心轨迹生成
给定参考的ZMP轨迹，对应最小能耗的CoM轨迹应该满足式(7)提出的目标函数。在文献[8]中，通过改进文献[20]中的无约束优化方法，提出了能跟踪多种参考ZMP轨迹的CoM轨迹求解算法，并在LIPM模型中得到了应用。本文中，由于在式(13)中引用了等效ZMP和等效自然频率，仍然可以采用这种方法来求解3MLIPM下最优的质心轨迹。
2.2.1 问题描述
参考文献[21]，定义质心运动的不稳定成分(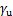
)和稳定成分(
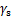)如下：
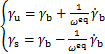(16)
利用式(13)，可以推导各分量的动力学模型：
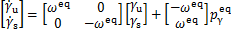(17)
跟踪参考的ZMP轨迹(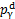
)，存在如下特解：
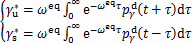(18)
定义各运动分量的误差项如下：
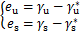(19)
由此，CoM轨迹可以通过下式决定：
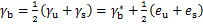(20)
其中，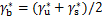
，为CoM的特解。
由此，给定参考ZMP轨迹后，由式(18)决定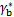
。然后，由误差项eu和es决定最优的CoM轨迹。
2.2.2 求解推导
根据UEWC定义，CoM轨迹被分为3段。为缩短篇幅，只讨论在SSPpre阶段质心轨迹的生成。其他具体推导过程可参见文献[8]。
结合式(17)和(19)，各分量误差求解如下：
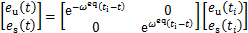(21)
因此，给定SSPpre终止时刻稳定运动分量的边界条件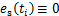
，式(20)中CoM轨迹计算如下：
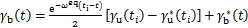(22)
考虑式(13)，该阶段的质心加速度求解如下：
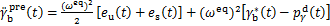
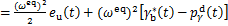(23)
不失普遍性，使用多项式型ZMP参考轨迹，表达形式如下：
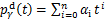(24)
式中：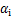
为多项式系数。
在文献[8]中，发现抛物线形ZMP轨迹(n=2)能充分地利用步行稳定支撑域并且能够简化计算。因此，本文也采用2次型函数。有
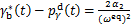(25)
最终，可以计算式(7)所示的目标函数如下：
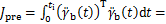
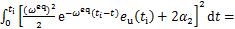
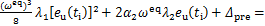
(26)
其中：W1，H1和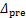
分别为二次项系数，一次项系数和常数项，
，
。
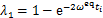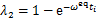为便于表达，引入以下变量：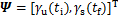
和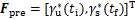
，则式(26)可以写成：
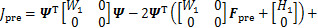
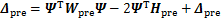(27)
式中：Wpre和Hpre分别为海森(Hessian)矩阵和一次项系数矩阵。
类似地，在SSPpost阶段，可以推导出：
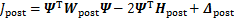(28)
式中：Wpost，Hpost和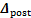
分别为对应的海森(Hessian)矩阵，一次项系数矩阵和常数项。具体推导过程可以见文献[8]。
在DSPtr阶段，可以推导出：
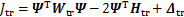(29)
式中：Wtr，Htr和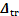
分别为对应的海森(Hessian)矩阵，一次项系数矩阵和常数项。
最终，式(7)中全局最优指标可以表达为
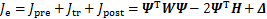(30)
式中：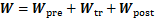
，
，
。
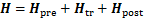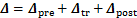最优边界条件求解为：
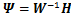(31)
利用该边界条件，可以求解出对应最小UEC的质心轨迹。
3 仿真与试验
3.1 数值仿真
利用Nao-H25机器人模型，进行步态生成和能耗评估的数值仿真。机器人样机和对应的三质点模型如图4所示。机器人总高度为58 cm，总质量为5.12 kg，每条腿各有5个自由度，行走过程中髋关节高310 mm。其他基本步行参数如表1所示。式(2)中躯干、支撑腿和摆动腿质心水平偏移量为0，躯干质心高度偏移量也为0。默认的步行周期为1.5 s，步长(L)为60 mm，步宽(W)为100 mm，摆动腿最大摆高为40 mm。
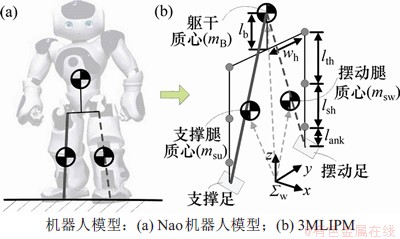
图4 Nao机器人与三质点模型
Fig. 4 Nao humanoid robot and three-mass model
表1 仿真参数设置
Table 1 Parameters setup for simulation
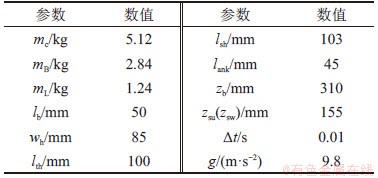
3.1.1 轨迹生成
为比较不同参考ZMP轨迹对步态生成结果和能耗的影响，文献[8]在3种常见ZMP参考轨迹的基础上提出一种抛物线形轨迹。本文也使用这4种轨迹。以前向运动为例，这4种参考轨迹分别为：ZMP在单足相无位移且瞬间切换(ZMP-dot(无DSP))，有双足支撑但ZMP在单足相期间无位移(ZMP-dot)，有双足支撑且ZMP在单足相期间做直线运动(ZMP-line)，有双足支撑且ZMP在单足相期间做抛物线运动(ZMP-parabola)。以步长6 cm为例，参考ZMP轨迹如图5(a)所示(双足相占整个周期15%)。此外，行走过程中，摆动腿水平轨迹通过2次多项式插值获得。在有双足支撑相和无双足支撑相时，左足和右足的水平摆动轨迹如图5(b)所示。
从图5(a)可见：利用足部稳定支撑域，可以给出不同形式的ZMP轨迹。本例中，在直线和抛物线形ZMP参考轨迹中，在SSPpre和SSPpost阶段，ZMP分别移动10 mm。跟踪该参考轨迹，生成的躯干质心位置、速度、加速度和等效ZMP轨迹见图6。
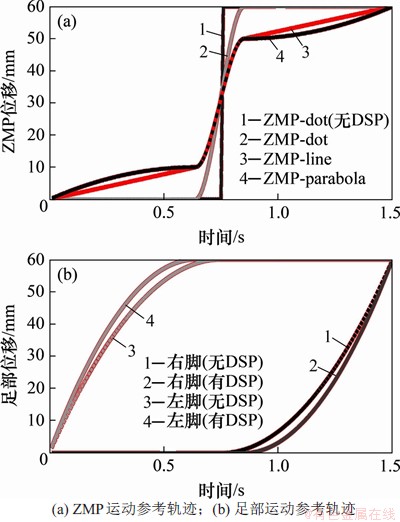
图5 ZMP与足部运动参考轨迹
Fig. 5 Reference trajectories for ZMP movement and foot movement
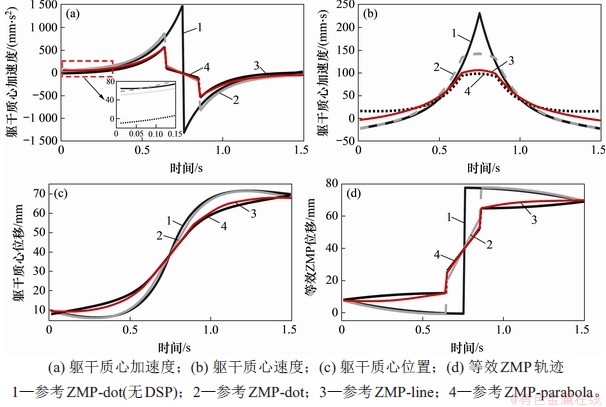
图6 不同参考ZMP轨迹下生成的质心加速度，速度，位置和对应的等效ZMP轨迹
Fig. 6 Generated CoM accelerations, velocities, positions and equivalent ZMP trajectories when using different ZMP trajectories
结合图6(a)(尤其是局放大图)和图6(b)可以发现，当使用这4种参考ZMP轨迹时，由于摆动腿质量的运动，在UEWC开始阶段，式(1)所假设的质心运动关系不严格成立。此外，当UEWC临近结束时，也出现同样的现象。但是，进一步分析图6(a)和图6(b)，发现该阶段只持续很短一段时间，并且这段时间内质心加速度和速度都很小。因此，这一段的运动对总体能耗的影响有限。仍然可以认为式(1)在整个UEWC内成立。
观察图6(b)可发现：无论使用何种参考轨迹，在初始和终止时刻的躯干质心速度都远小于中间时刻的躯干质心速度。因此，式(5)的推论成立，可以认为得到最优指标(7)的推导过程合理。
在一个UEWC内，各ZMP参考轨迹下对应的评价函数值(Je)和名义单位能耗(En)见表2。作为对比，同样使用图5(a)所示的ZMP参考轨迹，单质点LIPM模型对应的评价函数值和名义单位能耗也一并列出。
表2 不同ZMP参考下前向运动所需能耗
Tab.2 Energy costs needed by forward motion when using different reference ZMP trajectories
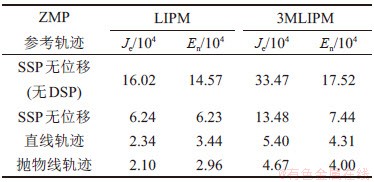
从表2可见：无论是利用LIPM还是3MLIPM，系统名义能耗(En)都随着ZMP可行域的充分利用而降低，并且抛物线形ZMP轨迹所对应的能量消耗最小。同样地，相应的能耗评价函数(Je)也逐渐减小，表明本文提出的基于质心加速度优化的能耗评价函数能反映步行系统实际能耗。
但是，从图6(d)中看出，由于考虑了腿部质量块的摆动，使用3MLIPM时的等效ZMP轨迹产生了明显的附加运动，进而导致了额外的躯干质心运动(图6(c))和额外的能量消耗。以同样使用抛物线形ZMP参考轨迹为例，3MLIPM对应的单位能耗En为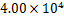
，明显大于LIPM对应的
。下文将修正3MLIPM的迈步参数输入，进一步减少步行能耗。
3.1.2 不同模型总体能耗性能分析
综合考虑矢状面和冠状面内的运动，比较LIPM和3MLIPM时的单位步行总能耗。针对腿部质量块摆动导致的躯干质心附加运动，提出用于3MLIPM的修正算法以跟踪目标落脚点并降低能量消耗。
给定参考步长、步宽、步行周期以及单足相期间ZMP的期望移动距离，即可确定参考ZMP轨迹。上述分析发现，直接利用3MLIPM时，等效的ZMP轨迹产生了附加运动并且最终导致更多的能耗。由图7所示3MLIPM对应的等效ZMP曲线可见：此等效轨迹对应的等效步长和步宽与期望步长和步宽有较大的偏差(图7中3个圆点代表期望落脚点)。因此，为实现预定的行走目标(即跟踪参考步长和步宽)并降低所需的能量消耗，提出一种基于二分搜索的修正算法(称为3MLIPM-mod)，用于校正名义步长和步宽输入。以步长校正为例，校正算法流程可分为3步：
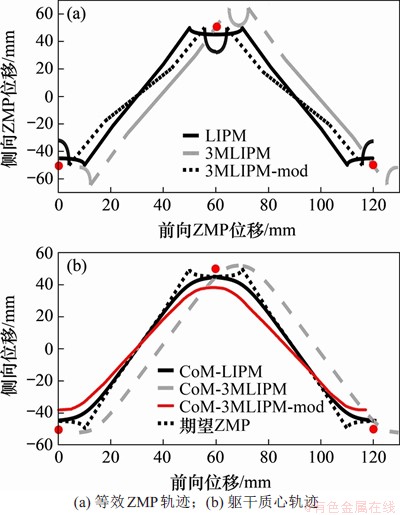
图7 3种方法生成的等效ZMP轨迹与躯干质心轨迹
Fig. 7 Equivalent ZMP trajectories and body CoM trajectories generated by three methods
1) 设定目标步长和0步长为初始的步长上边界和下边界，分别记为Lmax和Lmin，使用式(14)计算等效ZMP轨迹，并记录2条等效ZMP轨迹终止时刻的位移分别为Pmax和Pmin；
2) 取Lmax和Lmin的1/2作为新的步长，计算对应的等效ZMP轨迹，并按照二分法思想更新Pmax和Pmin以及Lmax和Lmin；
3) 循环步骤2)，直到Pmax与Pmin与目标落脚点的误差小于给定的边界，以对应的步长作为校正后的步长输入。
以期望步长为60 mm，步宽为100 mm为例，经校正后输入步长和步宽应分别为58 mm和78 mm。
最终，3种方法生成的等效ZMP轨迹对比如图7(a)所示。观察3MLIPM-mod对应的等效ZMP曲线，基本实现以预定落脚点为中心的运动。生成的躯干质心轨迹如图7(b)所示(圆点为目标落脚点位置)。其中“期望ZMP”表示LIPM和3MLIPM的参考ZMP轨迹。从图7(b)可见：利用3MLIPM-mod方法生成的质心轨迹侧向偏摆明显减少。以2个UEWC为例，3种策略下名义能耗对比见图8。显然，经过修正，3MLIPM-mod获得最佳的能耗表现。同时，利用抛物线形ZMP参考轨迹，获得了最小能耗。
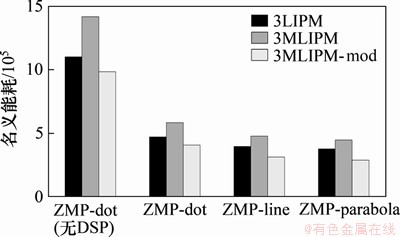
图8 3种方法下不同ZMP参考轨迹对应的能耗
Fig. 8 Nominal energy cost needed by three methods when using different ZMP references
3.2 样机试验
3.2.1 试验环境设置
试验中，机器人行走过程中的能量消耗反映在各关节所消耗的电能上。在一定时间内，机器人总能耗计算如下：
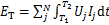(32)
式中：N为关节总数；Uj和Ij分别为各关节电机电压和电流；T1和T2分别为步行的开始和终止时间。
默认的行走步长为60 mm，步宽为100 mm，步行周期为1.5 s，双足相占比为15%。机器人底层通讯频率为100 Hz。试验过程中机器人行走总距离为500 mm。为了减轻躯干摆动，采用PD反馈控制器调整上半身姿态。为保证试验结果的准确性，每组步态分别进行5次试验，将平均值作为最终结果。使用python语言进行编程，在主频2.8 GHz的单核CPU上，每个控制循环(包括CoM轨迹生成和关节角度的逆运动学求解)在2 ms内完成，因此，本文提出的步态生成算法能够满足实时应用需求。
3.2.2 试验结果
考虑机器人驱动能力和关节运动范围限制，只使用带有双足相的参考ZMP轨迹。此外，通过3.1节的分析，使用3MLIPM-mod策略以生成三质点模型下的躯干质心轨迹。同时，也进行单质点模型试验以作为对比。以使用抛物线形ZMP参考轨迹为例，利用3MLIPM-mod策略时机器人某次行走的实际ZMP和CoM轨迹如图9所示(长方形代表每个足部落脚区域)。从图9可见：虽然实际ZMP和CoM有比较大的晃动，但是ZMP轨迹始终处在步行支撑域以内，实现了稳定行走。
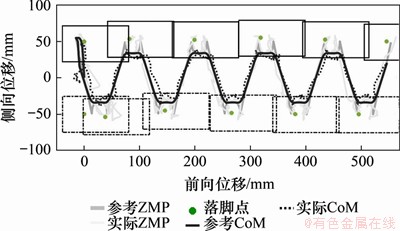
图9 抛物线形参考ZMP轨迹下参考轨迹与实际轨迹对比
Fig. 9 References and real trajectories of bipedal walking when using the parabolic ZMP reference
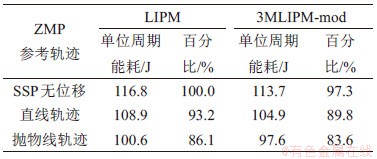
表3所示为使用LIPM和3MLIPM-mod下机器人在使用不同参考ZMP轨迹对应的能量消耗。由表3可见：抛物线形参考轨迹可以更好地利用足部支撑域以实现节能行走。如利用LIPM和3MLIPM-mod时，抛物线形ZMP对应的能耗分别是固定ZMP轨迹时能耗的86.1%和85.8%。此外，在同一参考ZMP轨迹下，3MLIPM-mod所需的能耗都比LIPM的要小，因此，修正三质点模型后，可以有效降低系统能耗。结合ZMP稳定域的利用，最终，使用抛物线参考轨迹的三质点模型比使用固定ZMP参考轨迹的单质点模型节能16.4%。
表3 不同模型下机器人实际能耗
Tab.3 Actual energy cost of bipedal walking when using different models
4 结论
1) 面向三质点模型，以集中质量跟踪目标轨迹所需要的能量输入作为系统能耗，提出了以加速度平方和最小为目标的二次型能耗评估函数。该指标能反映系统能耗，并且能够直接指导质心轨迹的生成。
2) 基于二次型能耗评价函数，提出求解最优质心轨迹的无约束优化算法，该算法能跟踪不同形式的参考ZMP轨迹并能给出CoM解析解。试验表明该步态生成算法能满足实时性需求，生成的轨迹可行。
3) 为消除腿部质量摆动对导致的躯干质心的附加运动，使用基于二分搜索的修正算法，修正三质点线性倒立摆的步行参数输入。抛物线形参考轨迹能有效提高能量效率。修正后的三质点模型也有助于降低能耗。
参考文献：
[1] 颜云辉, 徐靖, 陆志国, 等. 仿人服务机器人发展与研究现状[J]. 机器人, 2017, 39(4): 551-564.
YAN Yunhui, XU Jing, LU Zhiguo, et al. Development and research status of humanoid service robots[J]. 2017, 39(4): 551-564.
[2] 张继文, 刘莉, 陈恳. 面向全方位双足步行跟随的路径规划[J]. 自动化学报, 2016, 42(2): 189-201.
ZHANG Jiwen, LIU Li, CHEN Ken. Omni-directional bipedal walking path planning[J]. Acta Automatica Sinica, 2016, 42(2): 189-201.
[3] 孙广彬, 王宏, 陆志国, 等. 仿人足底肌电特征的机器人行走规划[J]. 自动化学报, 2015, 41(5): 874-884.
SUN Guangbin, WANG Hong, LU Zhiguo, et al. Humanoid walking planning based on EMG from human foot-bottom[J]. Acta Automatica Sinica, 2015, 41(5): 874-884.
[4] 丁加涛, 何杰, 李林芷, 等. 基于模型预测控制的仿人机器人实时步态优化[J]. 浙江大学学报: 工学版, 2019, 53(10): 1843-1851.
DING Jiatao, HE Jie, LI Linzhi, et al. Real-time walking pattern optimization for humanoid robot based on model predictive control[J]. Journal of Zhejiang University (Engineering Science), 2019, 53(10): 1843-1851.
[5] 易江, 朱秋国, 吴俊, 等. 基于最优控制的仿人机器人行走振动抑制[J]. 机器人, 2018, 40(2): 129-135.
YI Jiang, ZHU Qiuguo, WU Jun, et al. Walking vibration suppression for humanoid robot based on optimal control[J]. Robot, 2018, 40(2): 129-135.
[6] COLLINS S, RUINA A, TEDRAKE R, et al. Efficient bipedal robots based on passive-dynamic walkers[J]. Science, 2005, 307: 1082-1085.
[7] 姚道金, 王杨, 姚渊, 等. 基于质心运动状态的双足机器人欠驱动步行稳定控制[J]. 机器人, 2017, 39(3): 324-332.
YAO Daojin, WANG Yang, YAO Yuan, et al. Stable control of underactuated bipedal walking based on motion state of center-of-mass[J]. 2017, 39(3): 324-332.
[8] DING Jiatao, ZHOU Chengxu, XIAO Xiaohui. Energy-efficient bipedal gait pattern generation via CoM acceleration optimization[C]// 2018 IEEE-RAS 18th International Conference on Humanoid Robots(Humanoids). Beijing, China: IEEE, 2018: 238-244.
[9] ZHANG Running, LIU Huaxin, MENG Fei, et al. Energy efficiency and speed optimization by squad-unit genetic algorithm for bipedal walking[C]// IEEE International Conference on Robotics and Biomimetics(ROBIO). Kuala Lumpur, Malaysia. IEEE, 2018: 661-667.
[10] ZHU Hongbo, LUO Minzhou, MEI Tao, et al. Energy-efficient bio-inspired gait planning and control for biped robot based on human locomotion analysis[J]. Journal of Bionic Engineering, 2016, 13(2): 271-282.
[11] SHIN H K, KIM B K. Energy-efficient gait planning and control for biped robots utilizing the allowable ZMP region[J]. IEEE Transactions on Robotics, 2014, 30(4): 986-993.
[12] KAJITA S, KANEHIRO F, KANEKO K, et al. The 3D linear inverted pendulum mode: a simple modeling for a biped walking pattern generation[C]// International Conference on Intelligent Robots and Systems. Expanding the Societal Role of Robotics in the the Next Millennium Maui, HI, USA: IEEE, 2001: 239-246.
[13] BRANDAO M, HASHIMOTO K, SANTOS-VICTOR J, et al. Footstep planning for slippery and slanted terrain using human-inspired models[J]. IEEE Transactions on Robotics, 2016, 32(4): 868-879.
[14] VUKOBRATOVIC M, BOROVAC B. Zero-moment point: thirty five years of its life[J]. International Journal of Humanoid Robotics, 2004, 1(1): 157-173.
[15] ERBATUR K, KURT O. Natural ZMP trajectories for biped robot reference generation[J]. IEEE Transactions on Industrial Electronics, 2009, 56(3): 835-845.
[16] LI T H S, SU Yute, LIU S H, et al. Dynamic balance control for biped robot walking using sensor fusion, Kalman filter, and fuzzy logic[J]. IEEE Transactions on Industrial Electronics, 59(11): 4394-4408.
[17] SATO T, SAKAINO S, OHNISHI K. Real-time walking trajectory generation method with three-mass models at constant body height for three-dimensional biped robots[J]. IEEE Transactions on Industrial Electronics, 2011, 58(2): 376-383.
[18] SATO T, SAKAINO S, OHNISHI K. Real-time walking trajectory generation method at constant body height in single support phase for three-dimensional biped robot[C]// 2009 IEEE International Conference on Industrial Technology. Gippsland, VIC, Australia: IEEE, 2009: 1-6.
[19] SHIN H K, KIM B K. Energy-efficient gait planning and control for biped robots utilizing vertical body motion and allowable ZMP region[J]. IEEE Transactions on Industrial Electronics, 2015, 62(4): 2277-2286.
[20] LANARI L, HUTCHINSON S. Optimal double support zero moment point trajectories for bipedal locomotion[C]// 2016 IEEE/RSJ International Conference on Intelligent Robots and Systems(IROS). Daejeon, South Korea: IEEE, 2016: 5162-5168.
[21] TAKENAKA T, MATSUMOTO T, YOSHIIKE T, et al. Real time motion generation and control for biped robot-2nd report: Running gait pattern generation-[C]// 2009 IEEE/RSJ International Conference on Intelligent Robots and Systems. St. Louis, MO, USA: IEEE, 2009: 1092-1099.
(编辑 秦明阳)
收稿日期： 2019 -12 -19; 修回日期： 2020 -02 -26
基金项目(Foundation item)：国家自然科学基金资助项目(51675385，51175383) (Projects(51675385, 51175383) supported by the National Natural Science Foundation of China)
通信作者：丁加涛，博士，从事双足步行研究；E-mail：jtdingx@163.com
