Reliability analysis of supporting pressure in tunnels based on three-dimensional failure mechanism
来源期刊:中南大学学报(英文版)2016年第5期
论文作者:李闻韬 罗卫华
文章页码:1243 - 1252
Key words:rectangular tunnel; limit analysis; failure mechanism; reliability analysis
Abstract: Based on nonlinear failure criterion, a three-dimensional failure mechanism of the possible collapse of deep tunnel is presented with limit analysis theory. Support pressure is taken into consideration in the virtual work equation performed under the upper bound theorem. It is necessary to point out that the properties of surrounding rock mass plays a vital role in the shape of collapsing rock mass. The first order reliability method and Monte Carlo simulation method are then employed to analyze the stability of presented mechanism. Different rock parameters are considered random variables to value the corresponding reliability index with an increasing applied support pressure. The reliability indexes calculated by two methods are in good agreement. Sensitivity analysis was performed and the influence of coefficient variation of rock parameters was discussed. It is shown that the tensile strength plays a much more important role in reliability index than dimensionless parameter, and that small changes occurring in the coefficient of variation would make great influence of reliability index. Thus, significant attention should be paid to the properties of surrounding rock mass and the applied support pressure to maintain the stability of tunnel can be determined for a given reliability index.
J. Cent. South Univ. (2016) 23: 1243-1252
DOI: 10.1007/s11771-016-0374-7
LUO Wei-hua(罗卫华)1, LI Wen-tao(李闻韬)2
1. College of Civil Engineering, Hunan University, Changsha 410082, China;
2. School of Civil Engineering, Central South University, Changsha 410075, China
 Central South University Press and Springer-Verlag Berlin Heidelberg 2016
Central South University Press and Springer-Verlag Berlin Heidelberg 2016
Abstract: Based on nonlinear failure criterion, a three-dimensional failure mechanism of the possible collapse of deep tunnel is presented with limit analysis theory. Support pressure is taken into consideration in the virtual work equation performed under the upper bound theorem. It is necessary to point out that the properties of surrounding rock mass plays a vital role in the shape of collapsing rock mass. The first order reliability method and Monte Carlo simulation method are then employed to analyze the stability of presented mechanism. Different rock parameters are considered random variables to value the corresponding reliability index with an increasing applied support pressure. The reliability indexes calculated by two methods are in good agreement. Sensitivity analysis was performed and the influence of coefficient variation of rock parameters was discussed. It is shown that the tensile strength plays a much more important role in reliability index than dimensionless parameter, and that small changes occurring in the coefficient of variation would make great influence of reliability index. Thus, significant attention should be paid to the properties of surrounding rock mass and the applied support pressure to maintain the stability of tunnel can be determined for a given reliability index.
Key words: rectangular tunnel; limit analysis; failure mechanism; reliability analysis
1 Introduction
Because of its practical importance, the analysis of tunnel stability has received great attention in the literature. Limit analysis theory have been successively applied to the study of this problem. FRALDI and GUARRACINO [1-3] firstly introduced an exact solution for the evaluation of collapse mechanisms in the cross-section tunnel. The collapse mechanism of tunnel vault established under three-dimensional condition. The works are of significant importance but they ignored the supporting pressure when the virtual work equation performed. YANG et al [4-7] extended this collapse mechanism and other factors were considered in their researches. Based on the previous studies and through a detailed analysis, this work presents a more practical collapse mechanism of tunnel vault under three- dimensional condition.
Over the decades, reliability assessments have been widely used to evaluate the stability of tunnels. In reliability analysis, the first-order reliability method (FORM) and Monte Carlo method are frequently applied. MOLLON et al [8-10] studied the failure probability of tunnel face stability via the FORM with reference to Mohr-Coulomb failure criterion. This work presents an analysis of the possible collapse of tunnel roof in Hoek- Brown rock mass. Random variables are considered as independently distributed to compute the reliability index and the probability of failure of the tunnel. Sensitivity analysis and the study of the coefficient of variation and partial safety factors are also performed.
2 Three-dimensional limit analysis of tunnels with nonlinear criterion
2.1 Nonlinear Hoek-Brown criterion
Hoek and Brown introduced their failure criterion which links the equation to the actual characteristics of the rock mass in 1980. The criterion started from the research of intact rock so it was generally used to evaluate tightly interlocked hard rock mass. Factors were then introduced to Hoek-Brown criterion on the basis of the characteristics of joints in a rock mass. Through decades of development, the latest Hoek-Brown criterion defined by [11-12]
 (1)
(1)
where σ1 and σ3 are the major and minor effective principal stresses at failure; σci is the uniaxial compressive strength of the intact rock material; mb , s and a are material constants, where s=1 for intact rock. On the other hand, Hoek-Brown criterion can also be used to relate normal and shear stresses. In this situation, Hoek-Brown criterion can be defined by
 (2)
(2)
where A and B are material constants; σn is the normal effective stress, and σt is the tensile strength of the rock mass. Hoek-Brown failure criterion was widely used to analyze the property of rock mass [13-15]. In applying the Hoek-Brown failure criterion, expressed in effective stress terms, to practical design problems it is necessary to determine the property of the rock mass. There is no preferred failure direction in Hoek-Brown criterion and the rock mass is treated as isotropic. For these features, Hoek-Brown criterion can be used to incorporate real rock properties in a limit analysis procedure.
2.2 Limit analysis theory
Limit methods, including limit analysis method, limit equilibrium method, and slip line method are based on closely simple model of soil, and their major advantage is to solve the stability problem of rock-soil. In these methods, both limiting equilibrium method and slip line method focus on stress equilibrium and yield condition rather than on the fact that stress-stain relationship is the fundamental element in continuum theory of solid. As a matter of fact, the main difficulties arising in these methods lie in modeling and validation of results. Essentially, the boundary condition of rock-soil should include both stress and strain in order to get relatively precise consequence. Limit analysis was studied as a subtopic in metal plastic theory. Unlike the methods given above, limit analysis method regards rock-soil as ideal elastic-plastic material and the relationship between stress and strain was introduced to the stability analyses of rock-soil in the associated flow rule. YANG et al [16-19] had extensively applied limit analysis in stability analysis of tunnels and rock slopes. Specifically, limit analysis theory is composed of two parts as upper bound theorem and lower bound theorem and the upper bound theory could be concluded. In a kinematically admissible velocity field which satisfies the velocity boundary condition and the compatibility between the strain rates and velocity, according to virtual work-rate equation [20-22]:
 (3)
(3)
where 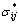 and
and  are the rate of stress and the rate of train in a kinematically admissible velocity field respectively; Ti and Xi are the surface force and the body force of studied object, respectively; Vi is the velocity vector in a kinematically admissible velocity field. The determined load Ti and Xi are not lower than the collapse load.
are the rate of stress and the rate of train in a kinematically admissible velocity field respectively; Ti and Xi are the surface force and the body force of studied object, respectively; Vi is the velocity vector in a kinematically admissible velocity field. The determined load Ti and Xi are not lower than the collapse load.
2.3 Three-dimensional failure mechanism
FRALDI and GUARRACINO [1-3] firstly introduced an exact solution in the realm of the plasticity for the evaluation of collapse mechanisms in the cross- section of a rectangular tunnel. The advantage of the procedure lies in the extreme simplicity of the calculations required, which can give a meaningful physical insight into the parameters that hold the problem at hand. This method focuses on the kinematic of collapse rather than on the onset of plasticity, so it is precisely correspond to the actual collapse mechanism. Besides the Hoek-Brown criterion, other nonlinear failure criterion [23-26] was also applied in the analysis of failure mechanism. With reference to previous achievements, the collapse mechanism of tunnel vault was established in three-dimensional condition. Their works are of significant importance but they ignored the supporting pressure when equating the rate of external work with the rate of internal dissipation of energy. In tunnel engineering, supporting pressure offered by tunnel lining is a significant factor which may greatly influence the collapse mechanism.
Based on the previous studies [27-29] and through a detailed analysis, this work presents a more practical collapse mechanism of tunnel vault under three- dimensional condition. In this work, a deep buried rectangular tunnel was taken into analysis and the work rate of supporting pressure was used in the virtual work equation. Additional, the surrounding rock mass is supposed to be completely uniform.
With reference to Hoek-Brown failure criterion, plastic potential, ξ, can be written in the form as
 (4)
(4)
where A and B are dimensionless parameters characterizing the rock mass; τn and σn are shear stress and principal effective stress, respectively; σc and σt are the compressive and tensile stresses at failure, respectively.
According to flow rule and the physical equation of collapse surface, the dissipation density of the internal forces on the detaching surface at impending collapse is

 (5)
(5)

Fig. 1 Profile of three-dimensional collapse
where f ′(x) is the first derivative of the unknown detaching curve in X-Z plane; v is the velocity of collapse rock mass. A dot denotes differentiation with respect to time. The lateral area of collapsing rock mass is:
 (6)
(6)
The rate of internal dissipation of energy in collapsing surface is
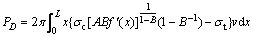 (7)
(7)
Gravity power is:
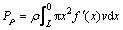 (8)
(8)
where ρ is the weight per unit volume of the rock mass; L is the radius of the collapsing underside. The power of supporting pressure is
 (9)
(9)
The rate of internal dissipation of energy minus the rate of external work so a function is defined as
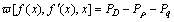 (10)
(10)
It can also be written as


 (11)
(11)
where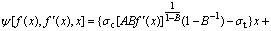
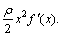 The first variation of the total dissipation
The first variation of the total dissipation  can be written as
can be written as
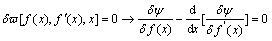 (12)
(12)
that is
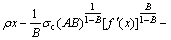
 (13)
(13)
After twice integrations, the form of collapsing curves f(x) is
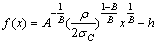 (14)
(14)
where h is the maximum height of the collapsing block. By equating the total dissipation Eq. (11) to zero and by means of some algebraic manipulations:
 (15)
(15)
Let f(L)=0, there is
 (16)
(16)
The collapsing curve f(x) in cross-section is then obtained as
 (17)
(17)
Expanding previous work to three-dimensional collapse mechanism, the equation of detaching curve is
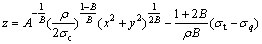 (18)
(18)
3 Reliability analysis of tunnels based on principle of maximum entropy
3.1 Principle of maximum entropy
The entropy of random variables means its uncertainty in the whole definition region. The greater value of entropy indicates the greater uncertainty of random variables. This is the so called principle of maximum entropy. According to the principle of maximum entropy, we can pick up such a distribution whose entropy could reach its maximum in order to obtain a distribution which is closer to the real distribution of random variables [30-34].
For continuous random variable X, entropy can be defined as
 (19)
(19)
where H is the entropy of random variable X; f(x) is the possibility density function of random variable X; R is the domain of definition. In order to get the maximum of target function H, Lagrange multiplier method could be used to construct Lagrange function.
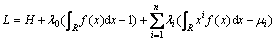 (20)
(20)
where λi is Lagrange multiplier. In order to obtain the maximum of Eq. (20), the following equation must be satisfied:
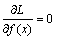 (21)
(21)
After a purely mathematic computation, the function of maximum entropy can be written as
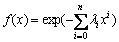 (22)
(22)
The constraint condition of function Eq.(7) is
 (23)
(23)
By substituting Eq.(8) into Eq.(9), there is
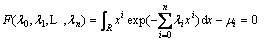
 (24)
(24)
Equation (24) could be solved via Newton iteration method, probability density function f(x) can be obtained by substituting λi into Eq.(22).
According to recent research achievement, it can be concluded that: 1) when the mean value and the variance of random variable X are constant, the probability density function (PDF) of X obeys the normal distribution; 2)when the geometric mean and the logarithmic standard deviation of random variable X are constant, the PDF of X obeys the lognormal distribution. In later discussion, the PDF of rock-soil parameters is assumed to be normally distributed or lognormally distributed with regard to the principle of maximum entropy.
3.2 Reliability analysis of tunnels
The first order reliability method (FORM) was firstly proposed, and was found of high acceptance as an approximation technique to assess the reliability of structure. Design point method was recommended by joint committee on structural safety (JCSS) so it is also called JCSS method.
In order to apply Rackwitz and Flessler method (RF method), non-normal random variables should generally transformed into standard normal ones through equivalent normalize transformations. According to equivalent normalization conditions, mean value  of equivalent normal distribution is:
of equivalent normal distribution is:
 (25)
(25)
And standard deviation  of equivalent normal distribution is
of equivalent normal distribution is
 (26)
(26)
where Φ(·) is the standard normal distribution function; and f(·) can be obtained from the table of standard normal distribution. After the equivalent normalization, the calculation steps of reliability index β can be calculated by following procedures.
Firstly, let the limit state equation be composed of several mutually independent random variables.
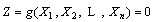 (27)
(27)
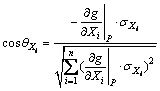 (28)
(28)
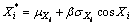 (29)
(29)
 (30)
(30)
 (31)
(31)
The new value of  should be substituted into computation steps (Eqs. (27) to (31)) until a constant
should be substituted into computation steps (Eqs. (27) to (31)) until a constant  occurred. In fact, errors may happen through equivalent normalize transformations so that Monte- Carlo simulation method (MCSM) was also widely used in engineering.
occurred. In fact, errors may happen through equivalent normalize transformations so that Monte- Carlo simulation method (MCSM) was also widely used in engineering.
In MCSM, large amounts of samples are generated according to the probability density of each variable. MCSM was supposed to be a relatively accurate method. According to the law of large numbers, we assume x1, x2, …, xn as individual random variables that obey to the same distribution. In another word, x1, x2, …, xn have the same mathematic expectation of μ and variance σ2. So, for any ε>0, there is
 (32)
(32)
Supposing in the n-times individual experiments, the frequency that event A occurs is m/n. For any ε>0, there is:
 (33)
(33)
where P(A) expresses the possibility that random event A occurred. In order to employ Monte-Carlo method to calculate the reliability index, we should presume the distribution type of random variables which influence the reliability of structure; use rational procedure to sample these random variables and substitute them to structure function; and count the number of times that structure failed to fing the frequency that structure failed is nf in the n-times individual experiments. The reliability of structure could be regard as
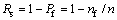 (34)
(34)
The reliability index obtained by MCSM could be seen as a precise value when the sample size of MCSM is big enough. The key to MCSM procedure lies in the generation of random variables. In this work, several small procedures based on MATLAB have been coded to calculate the reliability index according to MCSM.
3.3 Reliability analysis model of supporting pressure
According to the failure mechanism given above, it is easy to figure out the pressure caused by collapse block, so the minimum support pressure can be determined with reference to the degree of reliability. By following a purely geometry calculation, the weight of collapse block can be written as

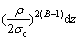


 (35)
(35)
Assuming the support pressure in the area of collapsing rock mass is

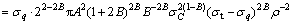 (36)
(36)
Let the weight of collapse block equals the corresponding support pressure, then
 (37)
(37)
After necessary simplification, one can get
 (38)
(38)
With reference to calculations above, the minimum support pressure that rectangular tunnel needed to maintain stability depends on the parameters of surrounding rock mass. It can also be written in the form as 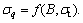
The aim of this paper is to perform a reliability analysis of the vault of deep buried rectangular tunnel. Due to the fact that the properties of rock mass are generally varied within a relatively wide range, objective function was solved by deterministic reliability requirement in different surrounding rock mass. The minimum results obtained are the necessary support pressure that rectangular tunnel needed to avoid collapse.
was solved by deterministic reliability requirement in different surrounding rock mass. The minimum results obtained are the necessary support pressure that rectangular tunnel needed to avoid collapse.
The deterministic failure model is based on the upper-bound method of the limit analysis theory. According to the objective function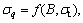 scalar parameter B and tensile strength σt are assumed as random variables in the calculations. The performance function utilized in reliability analysis is given as
scalar parameter B and tensile strength σt are assumed as random variables in the calculations. The performance function utilized in reliability analysis is given as
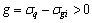 (39)
(39)
where σq is the support pressure and σgi is the weight of collapsing rock mass.
One may use another form of performance function 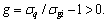 However, this leads exactly to the same value of the reliability index. In summary, the reliability model of deep buried rectangular tunnel can be defined as
However, this leads exactly to the same value of the reliability index. In summary, the reliability model of deep buried rectangular tunnel can be defined as
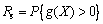 (40)
(40)
4 Probabilistic numerical results
For the analysis above, the minimum support pressure to maintain stability has significant correlation to the properties of surrounding rock mass. In particular, the difficulty of finding acceptable parameters for the given rock mass has been a problem since the publication of the Hoek-Brown criterion in 1980. In order to guarantee the accuracy of reliability index, both RF method and MCSM were adopted to analyze complex random variables, and the results obtained by these methods were then used for mutual authentication. In the following calculations, supporting pressure was substituted in the computation of reliability index as a random variable. By varying the applied support pressure, different reliability index and partial safety factors are calculated.
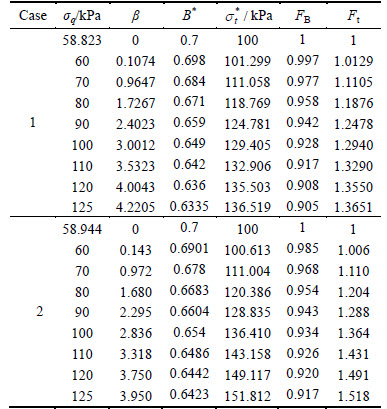
In the calculation to determine the reliability index corresponding to the given failure mechanism, the basic random variables should be identified firstly. As discussed above, the necessary supporting force given by tunnel lining only associated with tensile strength σt and dimensionless coefficient B of rock mass. In realistic geological environments, those parameters generally varied within a relatively wide range. For the probability distribution of those random variables, two cases are studied in the later discussion. In the first case, referred as to normal variables, σt and B are considered as normal variables. In the second case, referred to as non-normal variables, σt and B are considered to be lognormally distributed and these cases are listed in Table 1 in detail. It is also necessary to point out that the value of those two parameters are slightly lower than the typical properties for the average quality rock mass given by HOEK et al [11] and all the random variables are assumed to be independent. However, σq is regarded as normal variables in the calculation of both cases and the coefficient of variation is defined as 0.1 according to engineering data.
Table 1 Statistical values of random variables used in analysis

In order to determine the reliability index by the proposed algorithm, several small computer procedures have been coded to handle the repeatedly computation and iteration. In these calculations, support pressures are varied from 60 to125kPa to assess the influence of support pressure on the reliability results. Results are listed in Table 1.
For the failure mechanism given above, the collapse pressure of rock mass corresponding to normal variables was 58.823 kPa. On the other hand, for the lognormal variables, the collapse pressure was found to be 58.944 kPa.
Figure 2 shows that the plot of the reliability index versus the support pressure σq for both normal and non-normal rock parameters. It is easily observed that the reliability index increases with an increasing support pressure. One can also conclude that the results of non-normal variables are smaller than the one of normal variables so that supposing parameters to be lognormally distributed is conservative. For instance, results show that, when the support pressure is 120 kPa, the reliability index based on normal distributed parameters is 4.0 while the one based on lognormally distributed parameters is 3.75. It is also necessary to point out that the difference of reliability index between case 1 and case 2 is growing greater with the increase of support pressure. These results are of great importance, one can determine a target reliability index and then the minimum supporting pressure to maintain stability is able to be obtained.

Fig. 2 Reliability index versus σt for normal and non-normal variables
The values of the design points corresponding to increasing applied support pressure can give results of the partial safety factors of rock parameters σt and B as follows:
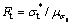 (41)
(41)
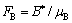 (42)
(42)
Table 2 shows the Rackwitz-Fiessler reliability index and the corresponding design point for increasing applied support pressure. All these results for normal and non-normal rock parameters are presented. In both cases, the partial safety factors increases with the applied support pressure varies from 60 to 125 kPa. This table also presents the tendency of partial factors according to increasing support pressure. In both case, the value of Ft is increasing with the increase of applied support pressure, while the value of FB is slightly decreases. The value of Ft varies from 1 to 1.5, and the value of FB is always slightly less than 1. As can be seen from the different values of reliability index β in two cases, it is clear that supposing σt and B as lognormally distributed variables is conservative to assuming as normally distributed variables. For partial safety factors, FB obtained in case 1 is always smaller than the one in case 2; to the contrary, Ft obtained in case 2 is always smaller than the one in case 1.
Table 2 Reliability index, design point, and partial safety factors
5 Influence factor analysis and result discussions
5.1 Influence of coefficient of variation
An additional practical problem is that the coefficient of variation (COV) of rock parameters always varies in a large range. For the better understanding of the influence of COV on reliability index, different statistical properties of random variables have been employed in the following research. In these researches, different values of COV of σt and B were used in the calculation of reliability index. As can be seen in Figs. 3 and 4, the COV of σt (or B) varies from 0.05 to 0.25 with a constant value of B (or σt) in case1 and case 2 to compute the reliability index.
Figures 3 and 4 show that the increase of COV of σt and B would cause the decrease of reliability index. For instance, with an applied support pressure of 120 kPa in case 1, the reliability index decreases from 4.839 to 3.154 when the COV of σt varies from 0.05 to 0.25.
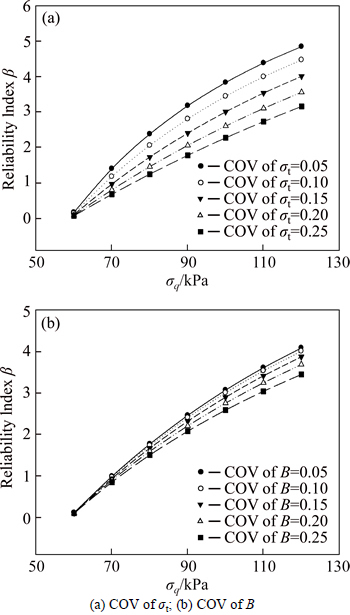
Fig. 3 Influence of coefficient of variation on reliability in Case 1:

Fig. 4 Influence of coefficient of variation on reliability in Case 2:
The decreases occur in case 2 by the change of COV are even more amazing. With the applied support pressure equals to 120 kPa, the reliability index decreases by 44.2% (4.84 to be compared to 2.70) if the COV of σt changes from 0.05 to 0.25. One can also observe that the same change happens in the COV of σt makes greater influence of reliability index than that of dimensionless parameter B in both case 1 and case 2. We can conclude that the COV of random variables (especially σt) would result in huge impact on reliability index so that great attention should be paid to the tensile strength.
5.2 Sensitivity discussions
The sensitivity factors give the importance of different variables in valuing reliability so that sensitivity analysis plays an increasingly vital role in reliability based design. Since KIUREGHIAN firstly indicated how to compute the sensitivity of the random variables, many approaches came up in recent studies. This paper chooses cosθXi to assess the relative importance of different affecting parameters, as shown in Eq.(28). The calculation results are listed in Table 3, where γt and γB represent the sensitivity of σt and B, respectively.
Table 3 Sensitivities and design points for different support pressures

As expected, the absolute value of γt is nearly three times larger than γB so it can be easily concluded that tensile strength σt plays a much more important role in reliability index. In both two cases, γt generally decreases with the increasing value of applied support pressure while γB only changes a little. With the support pressure increases from 60 to 120 kPa, the value of γt decreases by 26.7% (0.8061 to be compared to 0.5911), and the value of γB only changes from -0.2244 to -0.2285. It means that the influence of σt on reliability index is growing down on the condition of higher support pressure. One can also observe that the decreasing rate of γt in case 1 is faster than that in case 2, so great attentions should also be paid when variables are assumed as lognormally distributed.
5.3 Failure probability
In recent study of reliability problems, Monte-Carlo simulation method (MCSM) was considered as an efficient and accurate tool. In this work, MCSM was also selected to evaluate failure probability Pf according to different applied support pressure, but also to check the accuracy of RF method. As mentioned above, the accuracy of results obtained by MCSM based on the number of Monte-Carlo sample size. At first, a small research has been taken to test whether the sample size of Monte-Carlo simulation method is enough. In this research, the coefficient of variation (COV) of the failure probability versus the different sample sizes of MCSM was obtained when the applied support pressure equals to 80 kPa. Some computer programs have been written in MATLAB for these computations. In these procedures, a large amount of samples can be generated for the estimation of failure probability. Figure 5 plots the convergent tendency of COV of the failure probability.

Fig. 5 Coefficient of failure probability versus number of samples for correlated variables as given by MCSM
In both two cases, COV of the failure probability generally decreases with the increasing number of Monte-Carlo sample size. As can be seen from Fig. 5, the value of COV becomes smaller than 2% in both cases when the sample size increases to 20×104. What’s more, with the sample size comes to 40×104, the corresponding value of COV of failure probability was smaller than 1%.In the following calculations, failure probability is obtained from MCSM with a sample size of 100×104, so the result can be supposed as an exact value.
By varying the applied support pressure on tunnel lining, the failure probability was calculated by using RF method and MCSM for both two cases and the results are plotted in Fig. 6. As seen from Fig. 6, the plots of failure probability obtained by different methods are all in good agreement. For instance, the failure probability obtained by RF method is found to be 1.3×10-4 in case 1 with an applied support pressure of 100 kPa, while the failure probability obtained by MCSM equals to 1.6×10-4. This observation could be a demonstration for the accuracy of these two methods. For this reason, both RF method and MCSM can be seen as accuracy tool to analyze the value of reliability index. With an applied support pressure of 120 kPa, the failure probability of tunnel was less than 1×10-4 and the corresponding reliability index is found to be 3.719. This value of failure probability may be seen as safe enough in tunnel engineering.

Fig. 6 Comparison of failure probability obtained by RF method and MCSM
6 Conclusions
1) Based on the achievements of predecessors, the effective shape of the collapsing block is determined by equating the rate of external work with the rate of internal dissipation of energy. A rectangular tunnel is taken into three-dimensional analysis with the aim to construct a more practical collapse failure mode for the consideration of support pressure.
2) In the consideration of the randomness of soil parameters and its influence, reliability theory is utilized to calculate the failure probability of pressurized tunnel. The reliability index increases with the increasing of the applied support pressure. According to the reliability analysis, acceptable reliability index can be selected and the minimum supporting force of tunnel to maintain equilibrium was then obtained. For the failure mechanism, the collapse pressure of rock mass corresponding to different parameters of surrounding rock mass is obtained.
3) The small changes occurred in the coefficient of variation (COV) would greatly influence the reliability index. In the sensitivity analysis of random variables, the increase of COV of σt and B would result in the decrease of reliability index. One should also notice that tensile strength σt plays a much more important role in reliability index than dimensionless parameter B. In order to obtain a more precise result, the properties of surrounding rock should be well studied.
4) MCSM with a sample size of 100×104 is employed to calculate the reliability index. The reliability indexes obtained by RF method and MCSM are in satisfactory agreement, so these methods can be seen as accuracy tools to analyze the value of reliability index. For higher applied support pressure, the collapse reliability index becomes more acceptable.
References
[1] FRALDI M, GUARRACINO F. Evaluation of impending collapse in circular tunnels by analytical and numerical approaches [J]. Tunnelling and Underground Space Technology, 2011, 26(4): 507–516.
[2] FRALDI M, GUARRACINO F. Analytical solutions for collapse mechanisms in tunnels with arbitrary cross sections [J]. International Journal of Solids and Structures, 2010, 47(2): 216–223.
[3] FRALDI M, GUARRACINO F. Limit analysis of collapse mechanisms in cavities and tunnels according to the Hoek-Brown failure criterion [J]. International Journal of Rock Mechanics and Mining Sciences, 2009, 46(3): 665–673.
[4] YANG X L, HUANG F. Collapse mechanism of shallow tunnel based on nonlinear Hoek-Brown failure criterion [J]. Tunnelling and Underground Space Technology, 2011, 26(6): 686–691.
[5] YANG X L, HUANG F. Three-dimensional failure mechanism of a rectangular cavity in a Hoek–Brown rock medium [J]. International Journal of Rock Mechanics and Mining Sciences, 2013, 61: 189–195.
[6] YANG Xiao-li, QIN Chang-bing. Limit analysis of supporting pressure in tunnels with regard to surface settlement [J]. Journal of Central South University, 2015, 22(1): 303–309.
[7] YANG Xiao-li, LONG Ze-xiang. Roof collapse of shallow tunnels with limit analysis method [J]. Journal of Central South University, 2015, 22(5): 1929–1936.
[8] MOLLON G, DIAS D, SOUBRA A H. Range of the safe retaining pressures of a pressurized tunnel face by a probabilistic approach [J]. Journal of Geotechnical and Geoenvironmental Engineering, 2013, 139(11): 1954–1967.
[9] MOLLON G, DIAS, D, SOUBRA, A. Rotational failure mechanisms for the face stability analysis of tunnels driven by a pressurized shield [J]. International Journal for Numerical and Analytical Methods in Geomechancs, 2011, 35(12): 1363–1388.
[10] MOLLON G, DIAS D, SOUBRA A H. Probabilistic analysis and design of circular tunnels against face stability [J]. International Journal of Geomechanics, 2009, 9(2): 237–249.
[11] HOEK E, BROWN E T. Practical estimates of rock mass strength [J]. International Journal of Rock Mechanics and Mining Sciences, 1997, 34(8): 1165–1186.
[12] HOEK E, CARRANZA-TORRES C, CORKUM B. Hoek-Brown failure criterion [M]. Toronto: University of Toronto Press, 2002: 267–273.
[13] YANG X L, YIN J H. Upper bound solution for ultimate bearing capacity with a modified Hoek-Brown failure criterion [J]. International Journal of Rock Mechanics and Mining Sciences, 2005, 42(4): 550–560.
[14] YANG X L, YIN J H. Slope equivalent Mohr-Coulomb strength parameters for rock masses satisfying the Hoek-Brown criterion [J]. Rock Mechanics and Rock Engineering, 2010, 43(4): 505–511.
[15] SENENT S, MOLLON G, JIMENEZ R. Tunnel face stability in heavily fractured rock masses that follow the Hoek-Brown failure criterion [J]. International Journal of Rock Mechanics and Mining Sciences, 2013, 60(1): 440–451.
[16] YANG X L, WANG J M. Ground movement prediction for tunnels using simplified procedure [J]. Tunnelling and Underground Space Technology, 2011, 26(3): 462–471.
[17] YANG X L. Seismic passive pressures of earth structures by nonlinear optimization [J]. Archive of Applied Mechanics, 2011, 81(9): 1195–1202.
[18] YANG X L. Seismic bearing capacity of a strip footing on rock slopes [J]. Canadian Geotechnical Journal, 2009, 46(8): 943–954.
[19] YANG X L, LI L, YIN J H. Seismic and static stability analysis for rock slopes by a kinematical approach [J]. Geotechnique, 2004, 54(8): 543–549.
[20] YANG Xiao-li, LI Wen-tao, PAN Qiu-jing. Influences of anisotropy and in homogeneity on supporting pressure of tunnel face with kinematical approach [J]. Journal of Central South University, 2015, 22(9): 3536-3543.
[21] SOUBRA A H. Three-dimensional face stability analysis of shallow circular tunnels [C]// International Conference on Geotechnical and Geological Engineering. Melbourne, Australia: ICGGE, 2000: 19–24.
[22] SOUBRA A H, DIAS D. Three-dimensional face stability analysis of circular tunnels by a kinematical approach [J]. Geotechqiuue, 2008, 30(5): 894–901.
[23] YANG X L, YIN J H. Slope stability analysis with nonlinear failure criterion [J]. Journal of Engineering Mechanics, 2004, 130(3): 267–273.
[24] YANG X L, LONG Z X. Seismic and static 3D stability of two-stage rock slope based on Hoek-Brown failure criterion [J]. Canadian Geotechnical Journal, 2016, 53(3): 551-558.
[25] YANG X L. Seismic displacement of rock slopes with nonlinear Hoek-Brown failure criterion [J]. International Journal of Rock Mechanics and Mining Sciences, 2007, 44(6): 948–953.
[26] YANG X L. Upper bound limit analysis of active earth pressure with different fracture surface and nonlinear yield criterion [J]. Theoretical and Applied Fracture Mechanics, 2007, 47(1): 46–56.
[27] GEREMEW A M. Pore-water pressure development caused by wave-induced cyclic loading in deep porous formation [J]. International Journal of Geomechanics, 2011, 13(1): 65–68.
[28] VIRATJANDR C, MICHALOWSKI R L. Limit analysis of submerged slopes subjected to water drawdown [J]. Canadian Geotechnical Journal, 2006, 43(8): 802–814.
[29] PAUL M, Hoek E. Estimating the geotechnical properties of heterogeneous rock masses such as flash [J]. Bulletin of Engineering Geology and the Environment, 2001, 60(2): 85-92.
[30] ZHANG D B, SUN Z B, ZHU C Q. Reliability analysis of retaining walls with multiple failure modes [J]. Journal of Central South University, 2013, 20(10): 2879–2886.
[31] YANG X L, XU J S, LI Y X, YAN R M. Collapse mechanism of tunnel roof considering joined influences of non linearity and non-associated flow rule [J]. Geomechanics and Engineering, 2016, 10(1): 21-35.
[32] LOW B K, LACASSE S, NADIM F. Slope reliability analysis accounting for spatial variation [J]. Assessment and Management of Risk for Engineered Systems and Geohazards, 2007, 11(4): 177–189.
[33] ABDEL Y, MASSIH D S, SOUBRA A H. Reliability based analysis of strip footings using response surface methodology [J]. International Journal of Geomechanics, 2008, 8(2): 134–143.
[34] SU Y H, LI X, XIE Z Y. Probabilistic evaluation for the implicit limit-state function of stability of highway tunnel in China [J]. Tunnelling and Underground Space Technology, 2011, 26(2): 422–434.
(Edited by DENG Lü-xiang)
Foundation item: Project(2013CB036004) supported by National Basic Research Program of China
Received date: 2015-03-07; Accepted date: 2015-09-23
Corresponding author: LI Wen-tao; Tel: +86-15575965278; E-mail: 410801807@qq.com

