DOI: 10.11817/j.issn.1672-7207.2019.02.013
基于粒子群的改进智能算法在载荷识别中的应用
谢兵1, 2，谢博群3，张猛3，曲先强3
(1. 湘西南农村信息化服务湖南省重点实验室，湖南 邵阳，422000；
2. 湖南大学 信息科学与工程学院，湖南 长沙，410082；
3. 哈尔滨工程大学 船舶工程学院，黑龙江 哈尔滨，150001)
摘要：针对粒子群优化算法(PSO)无法处理反求问题中的病态问题，基于粒子群优化算法，通过遗传算法对粒子群优化算法进行改进，提出一种改进的粒子群优化算法(GAPSO)，通过载荷识别对该方法进行验证，并应用于静态载荷识别和动态载荷识别算例中。研究结果表明：改进后的粒子群优化算法既能使粒子群优化算法处理病态问题，又提高了反求问题的求解精度。
关键词：载荷识别；反问题；粒子群优化算法(PSO)；遗传算法
中图分类号：O342；TP311 文献标志码：A 文章编号：1672-7207(2019)02-0343-07
Application of improved intelligent algorithm based on particle swarm in load identification
XIE Bing1, 2, XIE Boqun3, ZHANG Meng3, QU Xianqiang3
(1. Key Laboratory of Information Service of Hunan Province for Rural Area of Southwestern Hunan,Shaoyang 422000, China;
2. College of Computer Science and Electronic Engineering, Hunan University, Changsha 410082, China;
3. College of Shipbuilding Engineering, Harbin Engineering University, Harbin 150001, China)
Abstract: Considering that particle swarm optimization algorithm(PSO) cannot deal with ill-posed problem, an improved particle swarm optimization algorithm(GAPSO) was proposed by genetic algorithm based on particle swarm optimization. This method was verified by common inversion problems such as load identification. Finally, the improved optimization algorithm was applied in static load identification and dynamic load identification. The results show that the improved particle swarm optimization algorithm can not only solve ill-posed problems, but also improve the accuracy of inverse problem.
Key words: load identification; inverse problem; particle swarm optimization algorithm(PSO); genetic algorithm
在工程结构分析中，经常需要在已知载荷情况下分析结构是否达到要求，但缺少有效的手段来获取载荷。一般地，获取结构应变相对简单，通过传感器获取应变，再利用有效的载荷识别方法获取实际的载荷形式。载荷识别是一类典型的反求问题，反求问题中存在病态现象[1]，即对于数据产生任意一种随机的扰动(例如传感器的测量误差)都会对识别结果产生很大的影响。当病态达到一定程度时，会使识别的载荷形式与实际载荷形式差别很大。反问题中都会存在1个目标函数，该目标函数一般表示为测量应变和识别应变之间的范数，通过合适的优化算法处理目标函数就可以得到实际载荷形式，因此，优化算法在在处理载荷识别问题中起着非常重要的作用。SUN等[2]提出了一种新的改进正则化算法，这种算法将改进正则化算子和L_curve方法混合用于处理病态情况下的载荷重新构建。WANG等[3]提出了一种新的迭代Tikhonov正则化方法，该方法被用于作用于实际工程结构中的多源动态载荷识别。LIU等[4]提出了一种基于Gegenbauer多项式展开和正则化方法的改进方法，该方法被用于随机结构中的动态载荷识别。CHOI等[5]使用正则化方法来研究并识别条件数的阈值，从而提高识别精度。朱南海等[6]提出了一种基于遗传算法的正则化方法，使用GCV准则、L曲线准则和Engl误差极小化准则作为优化函数，计算结果表明采用该方法可以很快达到优化解。马超等[7]提出了一种改进的正则化方法，针对噪声引起的载荷识别不适定性问题，可以有效抑制噪声，更可精确地识别载荷。姜鑫等[8]利用Tikhonov正则化方法(正则化参数由L曲线法确定)，针对工程结构中的Bernoulli-Euler梁结构，根据模态理论由梁上测点响应识别各阶模态激励，得到分布动载荷的各阶时间函数系数，还原Bernoulli-Euler梁结构上承受的分布动载荷。TONG等[9]提出了一种基于光滑约束的正则化方法，通过这种方法获取同震滑移反演的稳定解。ZHANG等[10]探究了在一定数量载荷模式下的5种反求方法的特性，然后使用这些方法来确定冰载荷的分布。随着对自然界优化现象的不断研究，一些用于描述自然界生物特性与正则化算法完全不同的智能优化算法被开发，包括粒子神经网络算法、模拟退火法、遗传算法等。其中，对于神经网络法[11]和遗传算法[12]已经有完整的matlab工具箱，通过优化算法之间不断融合，各种优化算法取长补短，在载荷识别中得到应用并取得了较好的识别效果。CAO等[13]采用一种人工神经网络方法用于载荷识别，发现不仅可以很快地收敛，而且精度较高。GHAJARI等[14]提出了一种人工神经网络方法用于冲击载荷历史进程构建。LEE[15]采用有限单元法和耦合遗传算法的反求方法，识别作用在桥面的动态载荷。NOH等[16]提出了一种使用耦合遗传算法的反求方法，这种方法使全局搜索成为可能。袭著有等[17]利用遗传算法，针对结构动载荷反演问题中的不适定问题，避免了传统载荷识别过程中产生的矩阵求逆病态、对初值敏感性以及累计误差等问题。但当载荷识别牵涉到病态问题时，粒子群优化算法的识别效果并不理想。为此，本文作者对粒子群优化算法进行改进，使该算法可以在病态问题中获得较好的识别效果。
1 优化算法的改进
1.1 基础算法
粒子群优化算法中每个粒子位置和速度的迭代方式为[11]：
(1)
(2)
式中：
和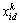
分别为粒子i在第k次时d维度下的速度和位置；
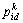为d维度下第i个个体在第k次时的最优位置；
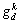为粒子群d维度下第k次时的最优位置；c1和c2为学习因子，在一般情况下，c1=c2=2；r1和r2为随机因子。
遗传算法的主要操作包括编码、确定适应度函数、选择、交叉和变异。通过使用GAOT遗传工具箱[12]中的相关函数来改进算法。
1.2 流程改进
在粒子群优化算法中，每一次迭代运算都会依据前一次迭代获取的粒子速度来更新现有的粒子速度，这种迭代更新方式保证粒子群优化算法有相对稳定的搜索方向，但这种稳定性在很大程度上降低了粒子群的多样性，因此，在病态问题中，添加一点波动都会使粒子群优化算法的结果严重偏离精确解。而相对于遗传算法这种启发式算法，虽然其内部的变异操作、交叉操作等具有概率性以及不定向性，表现为操作后子代可能好也可能坏，但这些操作也增加了种群的多样性，并且在一定程度上使遗传算法可以跳出局部最优解，搜索到优化解的可能性也会大大增加。因此，在该混合算法中，每次迭代除了使用粒子群优化算法本身的迭代方法以外，还通过遗传算法中的变异算子、交叉算子、选择算子针对粒子的位置和速度进行再次优化。该混合算法的具体操作流程如下。
1) 随机生成粒子群中每个粒子的速度与位置。首先给定粒子的位置和速度搜索范围，在这个范围内生成随机初始位置以及初始速度。
2) 确定粒子群中每个粒子的初始适应度并比较适应度较高的粒子作为当前最优粒子。
3) 进行迭代处理。粒子的位置和速度都作为染色体，通过RANKING函数对种群中染色体的适应度进行排序；通过SELECT函数对父代种群中的染色体进行选择以产生子代染色体；通过RECOMBINE函数对父代种群中的染色体进行交叉运算以产生子代染色体；通过MUT函数对父代种群中的染色体进行变异操作；通过REIN函数进行选择操作，从子代种群中选取染色体插入父代种群中组成新的种群，并且补足之前SELECT函数操作过程中去除的染色体数。
4) 对迭代后更新的每一个粒子位置以及粒子的速度使用粒子群优化算法更新。首先确定权重系数，针对每个粒子进行迭代。设定2个权重参数，其取值为[0.5，1.0]区间内的随机数，随后比较这2个参数，通过下式确定该次迭代的权重参数w：
(3)
式中：M为设定的迭代次数；t为当前迭代次数。
利用式(2)和式(4)迭代更新粒子群中各个粒子的位置和速度，式(1)改进形式如下：
(4)
在粒子群优化算法中，粒子的位置就是所需要的优化解，而粒子的速度决定了粒子位置的优化程度，因此，在遗传算法优化中，需要对粒子的速度以及位置同时进行优化。
5) 判定更新后最优解的适应度是否达到规定适应度或者迭代次数是否达到限定最大迭代次数。当有其中1项条件符合时即停止迭代，输出当前的优化解，否则，继续进行迭代更新直到满足1项条件为止。
在确定算法流程之后使用Matlab软件进行编程运算。图1所示为GAPSO的流程图。
2 优化算法的应用
在钢制闸门静态载荷识别和复合材料板冲击载荷识别的2个算例中，使用GAPSO与传统的正则化算法和粒子群优化算法进行计算和比较，以验证改进后优化算法的优势。
2.1 钢制闸门静态载荷识别
图2(a)所示为钢制闸门实物图，图2(b)所示为钢制闸门的有限元模型。
在闸门结构中，次横梁、小梁采用Q235钢，其余全采用Q345钢，在保证三维模型精度的前提下，采用壳体单元shell281 对三维模型进行网格划分，得到有限元模型。该有限元模型共有398 918个单元，1 190 776个节点。在有限元模型中，将闸门支臂尾端刚性固定于铰支点并约束铰支点所有线位移、铰支点绕x轴与y轴的角位移和闸门底部约束沿y方向的位移[18]。根据规范确定闸门的受力区域并将整块载荷加载区域划分成26个小的载荷加载区域，分别表示为A1~A26。图3所示为这26个载荷加载区域的分布位置。对A6区域施加载荷，图4所示为对A6区域施加载荷后的有限元仿真结果。
在获取仿真结果后，提取模拟钢板计的平均应变组成1列。类似于A6，依次对剩余的25个载荷加载区域依次施加载荷并提取平均应变组成系数矩阵，再利用优化算法识别出载荷并得到应变。最后，通过间接评估应变误差来确定载荷识别精度。利用下式对识别精度
进行判定：
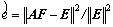(5)
式中：A为传递矩阵；F为载荷；E为测量应变。
利用2017-12-21，2018-01-05和2018-01-21这3 d的测量应变，应用GAPSO，PSO，tikh+gcv和tikh+l_curve进行载荷识别并得出各加载区域的载荷。在2017-12-21，2018-01-05和2018-01-21这3 d中，不同算法的载荷识别结果分别见图5、图6和图7。应用GAPSO和PSO以及2种正则化方法tikh+gcv和tikh+l_curve进行载荷识别并得出误差比较结果。因为PSO的误差相对其他3种(GAPSO，tikh+gcv，tikh+1_curve)反求算法的误差较大，因此，单独对PSO和GAPSO进行讨论。图8所示为GAPSO和PSO应变误差比较结果，图9所示为GAPSO和正则化方法应变误差比较结果。
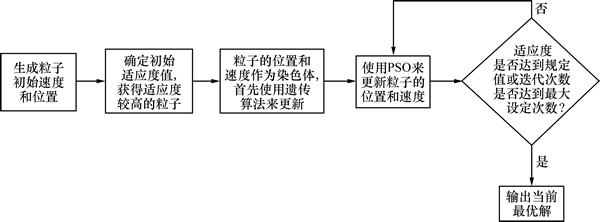
图1 GAPSO的流程图
Fig. 1 Flow chart of GAPSO
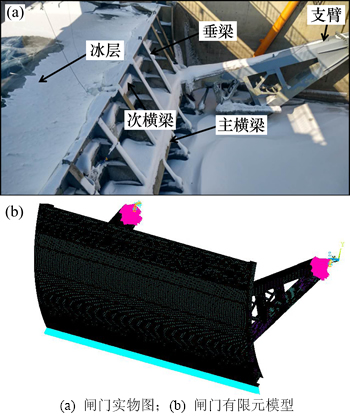
图2 闸门实物图和闸门有限元模型
Fig. 2 Three-dimensional model of steel gate
图3 载荷加载区域划分
Fig. 3 Loading area division
图4 A6区域施加载荷后仿真结果
Fig. 4 Simulation results of applied load at A6 area
图5 2017-12-21不同算法的载荷识别结果
Fig. 5 Load identification results of different algorithms on December 21,2017
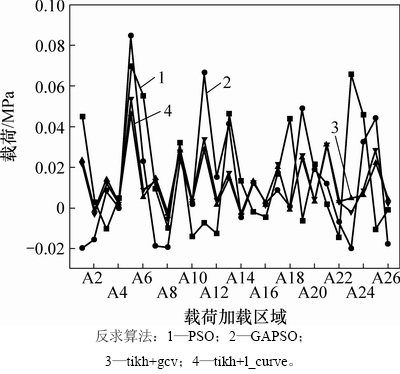
图6 2018-01-05不同算法的载荷识别结果
Fig. 6 Load identification results of different algorithms on January 5,2018
从图5~7可见：载荷的分布形式倾向于锯齿状，即在大多数情况下，上层板受到的载荷大于下层板受到的载荷。因为实际情况是上层板承受的是冰载荷，而下层板承受的是水压，冰载荷大于水压，故这4种方法的识别结果都与实际结果相符合。从图8可见：在2017-12-21，2018-01-05和2018-01-21这3 d中，GAPSO的应变误差远比PSO的小，该误差几乎可以忽略。从图9可见：由GAPSO得到的应变误差与tikh+gcv和tikh+1_curve正则化方法得到的应变误差相比，2017-12-21算法识别精度相当，而在2018-01-05，tikh+gcv的识别误差最大，tikh+l_curve和GAPSO的识别精度几乎相当；在2018-01-21，tikh+gcv的识别误差同样最大，其次是tikh+l_curve，误差最小的是GAPSO。综上可以得出：GAPSO的识别精度远比PSO的高；GAPSO的识别精度在最低的情况下也与tikh+gcv和tikh+l_curve这2种正则化方法相当。因此，可以认为GAPSO的识别精度最高。
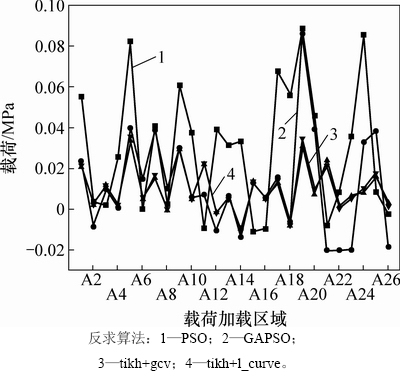
图7 2018-01-21不同算法的载荷识别结果
Fig. 7 Load identification results of different algorithms on January 21,2018
图8 GAPSO和PSO应变误差比较
Fig. 8 Comparison of strain error between GAPSO and PSO
图9 GAPSO和正则化方法应变误差比较
Fig. 9 Comparison of strain error between GAPSO and regularization methods
2.2 复合材料板冲击载荷识别
图10所示为复合材料板示意图。复合材料板上共有20个参考点，3个PZT传感器，传感器每隔0.02 s采集1个点；在参考点周边共划分88个敲击区域。首先由敲击20个参考点获取敲击载荷的时间以及由PTZ获取传感器的应变，依据载荷波动形式的范围构建参考系数矩阵。将参考点对应的3个参考系数矩阵叠放在一起，从而获得每个参考点的传递矩阵。表1所示为具体矩阵条件数。每个参考点附近有4个敲击面，敲击任意1个敲击面可获取应变，利用相邻参考点的传递矩阵可获取敲击面的冲击载荷时间，通过下式得出识别精度：
(6)
式中：Ai为第i个PZT传感器对应的传递矩阵；F为载荷；Ei为第i个PZT传感器对应的测量应变；S为PZT传感器的数量。
图10 复合材料板示意图
Fig. 10 Diagram of composite plate
由于敲击面过多，本文只列出3个敲击面(敲击面11，14和20)的敲击载荷识别结果。其中敲击面11和敲击面20靠近参考点2，敲击面14靠近参考点3，而参考点2和参考点3对应的参考矩阵条件数均大于1 000，故可以认为是病态问题[19]。应用GAPSO，PSO，tikh+l_curve和tikh+gcv这4种算法进行载荷识别。敲击面11，14和20的载荷-时间关系分别如图11~13所示。
表1 各参考点系数矩阵条件数
Table 1 Condition number of coefficient matrices
从图11~13可见：tikh+l_curve和tikh+gcv的识别结果几乎重合，在波峰部分比较接近真实值，而在非波峰部分则出现很大差异；PSO在波峰部分的识别结果与真实结果相差很大，而非波峰部分的结果接近真实结果；GAPSO在波峰部分的识别结果比2种正则化算法的识别结果好，在非波峰部分的识别结果同样接近真实值。从图12可以看出：在tikh+l_curve和tikh+gcv识别精度相对较低的情况下，GAPSO的识别精度仍提高。综上可以得出以下结论：GAPSO在波峰和非波峰部分都有较好的识别结果；tikh+l_curve和tikh+gcv在波峰部分有较好的识别效果；PSO在非波峰部分有较好的识别结果。因此，可以认为GAPSO的识别精度最高。
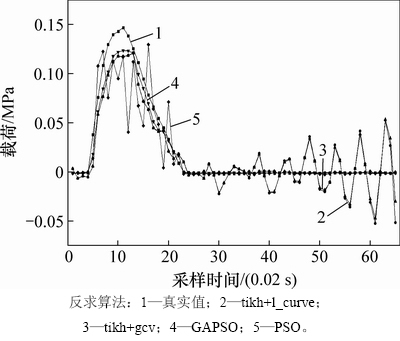
图11 敲击面11载荷与时间的关系
Fig. 11 Relationship between load and time at percussion surface 11
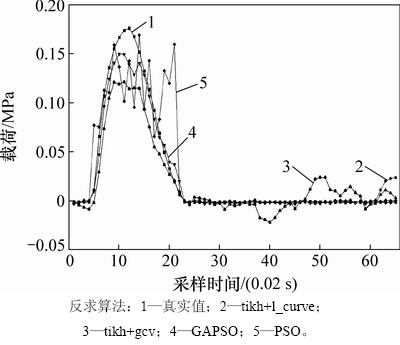
图12 敲击面14载荷与时间的关系
Fig. 12 Relationship between load and time at percussion surface 14
图13 敲击面20载荷与时间的关系
Fig. 13 Relationship between load and time at percussion surface 20
综合2个算例可以看出：改进后的粒子群优化算法(GAPSO)由于利用了遗传算法特有的处理方法，增大了粒子群算法中粒子的多样性，从而提高了粒子群优化算法的求解精度，该算法识别效果优于传统粒子群优化算法，尤其在处理病态问题时效果更加明显，甚至比传统正则化识别算法的识别效果好。
3 结论
1) 与PSO相比，GAPSO无论是在钢制闸门静态载荷识别算例中还是在复合材料板冲击载荷识别算例中，识别效果都有很大提高。与tikh+l_curve和tikh+gcv这2种正则化算法相比，GAPSO在静态载荷识别中具有相似的识别效果，在动态载荷识别中具有更好的效果，所以，总体上，GAPSO的识别效果最好。
2) 复合材料板冲击载荷识别算例是1个病态问题，从反求结果可以看出GAPSO的识别效果很好，而没有经过改进的粒子群优化算法识别效果很差，故GAPSO可以处理反求问题中的病态问题。
参考文献：
[1] TIKHONOV A N, GONCHARSKY A V, STEPANOV V V, et al. Numerical methods for the solution of ill-posed problems[M]. Dordrecht: Kluwer Academic Publishers, 1995: 28-34.
[2] SUN Xingsheng, LIU Jie, HAN Xu, et al. A new improved regularization method for dynamic load identification[J]. Inverse Problems in Science and Engineering, 2014, 22(7): 1062-1063.
[3] WANG Linjun, CAO Huiping, XIE Youxiang. An improved iterative Tikhonov regularization method for solving the dynamic load identification problem[J]. International Journal for Computational Methods in Engineering Science and Mechanics, 2015, 31(2): 292-293.
[4] LIU Jie, SUN Xingsheng, HAN Xu, et al. Dynamic load identification for stochastic structures based on Gegenbauer polynomial approximation and regularization method[J]. Mechanical Systems and Signal Processing, 2015, 56/57: 35-36.
[5] CHOI H G, THITE A N, THOMPSON D J. A threshold for the use of Tikhonov regularization in inverse force determination[J]. Applied Acoustics, 2006, 67(7): 700-702.
[6] 朱南海, 赵晓华. 基于遗传算法的Tikhonov正则参数优化计算[J]. 工程力学, 2009, 26(5): 26-27.
ZHU Nanhai, ZHAO Xiaohua. Optimal calculation of Tikhonov regularization parameter based on genetic algorithm[J]. Engineering Mechanics, 2009, 26(5): 26-27.
[7] 马超, 华宏星. 基于改进正则化方法的状态空间载荷识别技术[J]. 振动与冲击, 2015, 34(5): 146-147.
MA Chao, HUA Hongxing. State space load identification technique based on an improved regularized method[J]. Journal of Vibration and Shock, 2015, 34(5): 146-147.
[8] 姜鑫, 张方, 姜金辉. 基于模态坐标变换梁分布动载荷识别技术[J]. 国外电子测量技术, 2016, 35(2): 90-91.
JIANG Xin, ZHANG Fang, JIANG Jinhui. Technology in identification of distributed load for beam model based on model coordinate transform[J]. Foreign Electronic Measurement Technology, 2016, 35(2): 90-91.
[9] TONG Xiaozhong, XIE Wei, GAO Dawei. Regularized inversion for coseismic slip distribution with active constraint balancing[J]. Journal of Central South University, 2017, 24(12): 2962-2963.
[10] ZHANG Meng, QU Xianqiang, KALHORIB H, et al. Indirect monitoring of distributed ice loads on a steel gate in a cold region[J]. Cold Regions Science and Technology, 2018, 151: 267-287.
[11] 龚纯, 王正林. 精通MATLAB最优化计算[M]. 3版. 北京: 电子工业出版社, 2014: 38-60.
GONG Chun, WANG Zhenlin. Well versed in MATLAB optimization calculation[M]. 3rd ed. Beijing: Electronic Industry Press, 2014: 38-60.
[12] 雷英杰, 张善文, 李续武, 等. MATLAB遗传算法工具箱及应用[M]. 2版. 西安: 西安电子科技大学出版社, 2014: 40-51.
LEI Yingjie, ZHANG Shanwen, LI Xuwu, et al. MATLAB genetic algorithm toolbox and its application[M]. 2nd ed. Xi’an: Xidian University Press, 2014: 40-51.
[13] CAO X, SUGIYAMA Y, MITSUI Y. Application of artificial neural networks to load identification[J]. Computers and Structures, 1998, 69(1): 63-64.
[14] GHAJARI M, SHARIF-KHODAEI Z, ALIABADI M H, et al. Identification of impact force for smart composite stiffened panels[J]. Smart Materials and Structures, 2013, 22(22): 1-2.
[15] LEE S Y. An advanced coupled genetic algorithm for identifying unknown moving loads on bridge decks[J]. Mathematical Problems in Engineering, 2014, 9(4): 1-2.
[16] NOH M H, LEE S Y. Moving load identification in time domain using a coupled genetic algorithm[C]//International Conference, GST and SIA. Jeju, Korea: CCIS, 2012: 136-137.
[17] 袭著有, 闫云聚, 常晓通. 基于遗传算法的动态载荷识别优化方法[J]. 机械强度, 2015, 37(4): 594-595.
XI Zhuyou, YAN Yunju, CHANG Xiaotong. Optimization method of dynamic load identification based on genetic algorithm[J]. Journal of Mechanical Strength, 2015, 37(4): 594-595.
[18] 谢博群, 崔洪斌, 于泉海, 等. 松花江大顶子山弧形钢闸门静力数值仿真[J]. 邵阳学院学报(自然科学版), 2016, 13(4): 77-78.
XIE Boqun, CUI Hongbin, YU Quanhai, et al. Static numerical simulation of gate steel arc in Songhua River,Dadingzi Mountain[J]. Journal of Shaoyang University(Natural Science Edition), 2016, 13(4): 77-78.
[19] 曾群意, 欧吉坤. 用遗传算法解算病态方程[J]. 大地测量与地球动力学, 2003, 23(3): 94.
ZENG Qunyi, OU Jikun. Study on application of genetic algorithms in solving ill-conditioned equations[J]. Journal of Geodesy and Geodynamics, 2003, 23(3): 94.
(编辑 陈灿华)
收稿日期：2018-06-01；修回日期：2018-07-27
基金项目(Foundation item)：西部交通建设科技项目(2014364554050)；国家自然科学基金资助项目(61672356)(Project(2014364554050) supported by the Science and Technology Program of Western Transportation Construction,Ministry of Transport; Projects(61672356) supported by the National Natural Science Foundation of China)
通信作者：曲先强，博士，副教授，从事结构健康监测研究；E-mail：quxianqiang@hrbeu.edu.cn
