基于精细有限元分析的既有RC框架结构破坏机理
雷拓1,钱江2,刘成清3
(1. 长安大学 建筑工程学院,陕西 西安,710061;
2. 同济大学 土木工程防灾国家重点实验室,上海,200092;
3. 西南交通大学 土木工程学院,四川 成都,610031)
摘要:在三层既有框架结构现场推覆试验的基础上,建立该试验框架的精细化有限元模型。通过动力特性分析及Pushover分析,讨论试验框架的动力特性、荷载-位移曲线、钢筋应力及混凝土损伤分布,得到结构破坏过程中底层框架柱的剪力需求,并与各主要国家规范的抗剪承载力计算结果进行比较。研究结果表明:精细化模型能较好地模拟剪切破坏发生前试验框架的荷载-位移曲线,反映试验框架由于底层柱端配箍不足而导致的弯-剪破坏;各规范公式计算的抗剪承载力存在一定的离散性。
关键词:既有结构;钢筋混凝土;框架;精细化有限元;破坏机理
中图分类号:TU311.3 文献标志码:A 文章编号:1672-7207(2014)01-0214-09
Failure mechanism of an existing RC frame structure based on detailed finite element analysis
LEI Tuo1, QIAN Jiang2, LIU Chengqing3
(1. School of Civil Engineering, Chang’an University, Xi’an 710061, China;
2. State Key Laboratory of Disaster Reduction in Civil Engineering, Tongji University, Shanghai 200092, China;
3. School of Civil Engineering, Southwest Jiaotong University, Chengdu 610031, China)
Abstract: Based on the in-situ pushover test of a three-story existing frame,a finite element model of the testing frame was established. By means of dynamic property analysis and pushover analysis, the dynamic property, load-displacement curves, reinforcement stress and concrete damage distribution of the frame were studied. The shear demand of bottom columns during the failure process was obtained and then compared with the shear capacity calculated with several national design codes. The results show that the detailed finite element model can accurately simulate load-displacement curves of the test before shear failure happening and reflect flexure-shear failure pattern of the testing frame characterized by insufficient transverse reinforcement of bottom columns well. There are some discrepancies of shear capacity among the national codes.
Key words: existing structure; reinforced concrete; frame; detailed finite element; failure mechanism
GB 50011—2010(《建筑抗震设计规范》)的颁布实施,以及将要颁布的新版《中国地震动参数区划图》无疑将进一步提升我国新建建筑的抗震防灾能力。对于大量仍在使用的既有结构,由于所依据的设计标准较低,往往具有较高的易损性,因此,对此类结构的抗震性能重新评价及加固,成为减轻未来地震灾害的重要途径。为探究既有结构的破坏机理,我国台湾地震工程研究中心2005—2007年先后完成一系列学校建筑的现场推覆试验[1-3]。Corte等[4]进行一栋二层钢筋混凝土框架(含填充墙及楼梯)加固前后的现场推覆试验。Sharma等[5]进行一栋四层既有混凝土框架结构的足尺模型试验和计算分析。田颖等[6-7]基于通用梁柱有限元模型研究既有结构的抗震性能。区别于新结构设计,既有结构的体系、材料、截面和构造不能改变,既有结构性能化抗震评估面临更大的困难[8]。震害和试验研究表明:既有钢筋混凝土框架结构普遍的破坏特征是柱发生弯-剪破坏、剪切破坏以及节点区的剪切破坏[5, 9-10]。鉴于通用梁柱单元模型在模拟上述破坏时存在的不足,对既有结构破坏机理的研究,需要更精细的分析模型,以考虑结构、构件各种可能的破坏模式。本文作者在已完成的三层混凝土框架结构现场推覆试验的基础上,建立该框架的精细化有限元模型,讨论试验框架的动力特性、荷载-位移曲线、钢筋应力及混凝土损伤分布等,以期为后续建立可靠的既有结构简化分析模型提供依据。
1 试验框架概况
同济大学机电厂厂房为一栋建于1983年的3层钢筋混凝土框架结构。结构平面尺寸为40.48 m×33.40 m,层高分别为4.84 m(底层)、4.18 m(第2层)、4.18 m(第3层)。楼板为120 mm厚混凝土预制板,上铺60 mm厚现浇层;外墙厚240 mm,烧结普通砖砌筑。推覆试验时,选取厂房东南角切割而成的单跨单开间框架为试验对象(图1),保留梁L7-1和L7-2位置处的外墙。P1~P6为试验的6个加载点。各框架梁、柱尺寸及配筋详见文献[9]。从梁、柱配筋看,试验框架不满足现行抗震设计规范[11]的构造要求。
2 精细有限元模型的建立
2.1 梁和柱的模拟
梁、柱混凝土采用ABAQUS程序的C3D8R实体单元模拟。选用混凝土损伤塑性模型,模型参数取值如表1所示。表1中: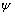 为膨胀角,取30°[12];
为膨胀角,取30°[12];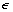 为塑性势偏心率;
为塑性势偏心率;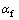 为双轴极限抗压强度与单轴极限抗压强度的比值;Kc为拉伸子午面上和压缩子午面上的第二应力不变量的比值;μ为黏性系数。
为双轴极限抗压强度与单轴极限抗压强度的比值;Kc为拉伸子午面上和压缩子午面上的第二应力不变量的比值;μ为黏性系数。
表1 混凝土模型参数
Table 1 Parameters of the concrete model

选用《混凝土结构设计规范》[13]推荐的混凝土单轴受压应力-应变曲线。基于应力-开裂应变的方式定义混凝土的受拉软化,并假定混凝土达到受拉峰值应力前,为线弹性;峰值应力后,混凝土受拉应力-应变关系由式(1)确定[14]。
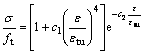 (1)
(1)
其中:ft为混凝土抗拉强度;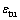 为极限拉应变,为考虑钢筋与混凝土黏结力对混凝土抗拉的效果,
为极限拉应变,为考虑钢筋与混凝土黏结力对混凝土抗拉的效果,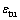 取0.005;c1和c2分别取 9.0和5.0[14]。关于损伤因子,目前还没有公认的确定方法。参考文献[15],采用式(2)~(4)定义混凝土受压损伤因子dc和受拉损伤因子dt。
取0.005;c1和c2分别取 9.0和5.0[14]。关于损伤因子,目前还没有公认的确定方法。参考文献[15],采用式(2)~(4)定义混凝土受压损伤因子dc和受拉损伤因子dt。
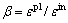 (2)
(2)
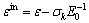 (3)
(3)
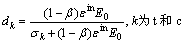 (4)
(4)
其中:下标t和c分别代表混凝土拉伸和压缩状态;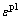 和
和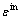 分别为混凝土的塑性应变和非弹性应变(考虑损伤后,
分别为混凝土的塑性应变和非弹性应变(考虑损伤后,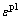 ≠
≠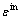 );
);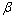 为塑性应变与非弹性应变之比,受压取0.35~0.70,受拉取0.50~0.95;
为塑性应变与非弹性应变之比,受压取0.35~0.70,受拉取0.50~0.95;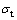 和
和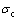 则分别为与混凝土应变
则分别为与混凝土应变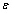 相应的拉、压应力;E0为混凝土初始弹性模量。
相应的拉、压应力;E0为混凝土初始弹性模量。
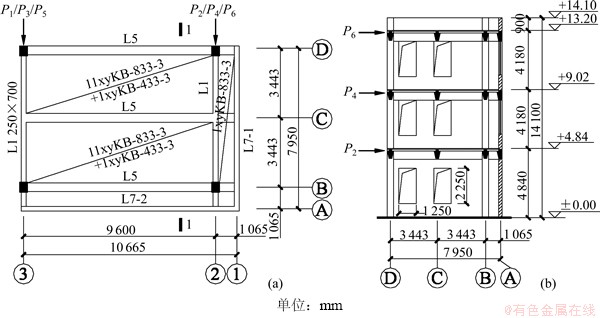
图1 试验框架结构布置
Fig. 1 Structural layout of testing frame
混凝土抗压强度以钻芯取样试验结果为准[9],抗拉强度ft取抗压强度的10%。当应力小于0.3~0.4倍抗压强度时,混凝土受压应力-应变曲线基本上接近直线;取0.4倍抗压强度前混凝土受压应力-应变曲线为直线,此时的割线刚度定义为初始弹性模量。
钢筋采用T3D2桁架单元模拟,将钢筋单元嵌入到混凝土实体单元中。钢筋材料模型选用ABAQUS的双线性随动强化模型,钢筋屈服后弹性模量取初始弹性模量的1%。钢筋材料强度及弹性模量以材性试验为准[9]。建模时,梁柱的纵筋、箍筋、弯起筋等与原型结构保持一致。
2.2 楼板和砖墙的模拟
楼板采用S4R壳单元模拟。从试验现象看,在整个试验过程中,楼板未发生明显的开裂。故在有限元分析时,楼板按弹性材料考虑,取弹性模量E为3.0×104 MPa,泊松比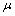 为0.2。
为0.2。
关于砖墙(砌体)的模拟,目前主要基于连续模型和等效斜撑模型。等效斜撑模型因其简单、高效而被广泛应用于框架填充墙结构的整体分析,但不能很好地模拟墙体裂缝的发展过程。连续模型计算精度较高,却又存在计算工作量繁重等问题;根据砖墙建模方式的不同,又分为2种:一种是将砖砌块、砂浆分别建模,并引入二者之间的黏结单元[16];另一种途径是将砖砌块、砂浆2种材料通过等效体积单元[17]的方法或试验方法等效成1种均质材料。本文作者采用连续S4R壳单元模拟砖墙。砖砌体材料用混凝土损伤塑性模型代替,模型参数如表2所示。
选用刘桂秋等[18]提出的砌体受压应力-应变关系,见式(5)~(6)。
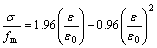 , 0≤
, 0≤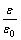 ≤1 (5)
≤1 (5)
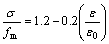 , 1≤
, 1≤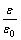 ≤1.6 (6)
≤1.6 (6)
其中,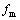 为砖砌体抗压强度;
为砖砌体抗压强度;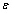 为砌体压应变,
为砌体压应变,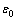 为砌体峰值应力
为砌体峰值应力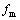 对应的应变,取0.003。
对应的应变,取0.003。
砌体受拉应力-应变的研究目前还不充分,为避免计算收敛困难,采用应力-断裂能的方式定义砌体的受拉行为,砖砌体的断裂能取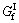 =20 N/m[19]。由于砌体材料缺乏损伤因子的研究,故未考虑砖砌体的受压损伤,受拉损伤的定义基于断裂能的方式。砖砌体抗压强度
=20 N/m[19]。由于砌体材料缺乏损伤因子的研究,故未考虑砖砌体的受压损伤,受拉损伤的定义基于断裂能的方式。砖砌体抗压强度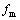 取3.0 MPa,抗拉强度为0.25 MPa。
取3.0 MPa,抗拉强度为0.25 MPa。
表2 砖墙模型参数
Table 2 Parameters of brick masonary model

2.3 梁与墙体及楼板的连接
试验框架的墙体位于主体框架外侧,且仅与梁L7-1和L7-2连接。准确模拟框架与砖墙的连接边界是比较困难的,从现有研究成果看,一种是采用线性界面单元[20],目前该方法还仅限于平面问题;另一种是采用接触单元[21]来处理砖墙与框架的连接,该方法的突出问题是参数确定困难且计算效率较低。本文采用铰接近似模拟砖墙与梁的连接,即通过ABAQUS的Tie Constraint建立外砖墙壳单元与框架梁实体单元的铰接连接。
从试验过程看,楼板未出现明显的开裂,说明试验过程中楼板处于较低的应力水平。故采用ABAQUS的Shell-to-Solid耦合实现楼板支撑边壳单元与梁实体单元的刚接连接。
2.4 有限元模型
图2所示为所建立的试验框架精细有限元模型。模型中采用实体单元55 632个,壳单元14 602个,杆单元53 370个,单元总数123 604个。
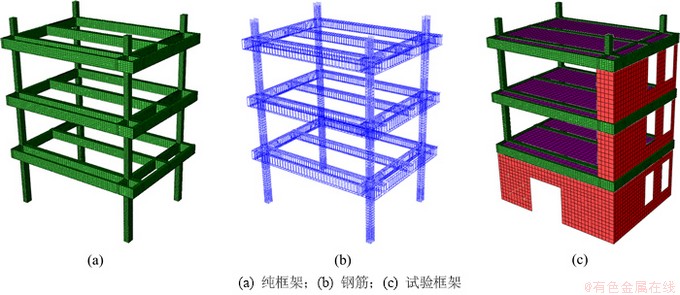
图2 试验框架有限元模型
Fig. 2 Finite element model of testing frame
3 计算结果与试验的对比
3.1 动力特性
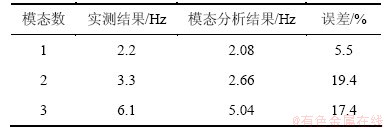
表3所示为模态分析与推覆试验前现场实测的试验框架动力特性对比情况,与实测结果较为吻合。
表3 动力特性对比
Table 3 Comparison of dynamic characteristics
3.2 荷载-位移曲线
图3所示为计算和试验所得荷载-位移曲线对比情况。从试验框架的基底剪力-顶点(P5点、P6点)位移曲线看,计算得到的结构极限承载力为859. 90 kN,P5点、P6点相应位移分别为162.75 mm和41.33 mm;与试验结果相比,极限承载力相对误差为0.18%,位移相对误差分别为9. 94%和21.81%。当P5点、P6点位移分别达到163.88 mm和41.43 mm时,因结构软化段的收敛性问题,计算终止;此时结构的基底剪力为850.01 kN。图3还给出试验框架基底剪力-位移(P1,P3,P2和P4点)曲线对比。总体来看,在底层③-B轴柱发生剪切破坏之前,计算结果与试验结果较吻合,计算模型能较好地模拟试验框架的整体性能。
4 结构应力及损伤
4.1 钢筋应力分析
图4和图5所示为加载历史中第11和14加载步时框架纵筋的应力变化云图。从图4和图5可见:
(1) 第11加载步时,③-B轴底层柱底部纵筋首先达到屈服,纵筋最大应力为328.1 MPa,此时,柱上部纵筋尚未屈服,最大应力为207.4 MPa。
(2) 第14加载步时,纵筋屈服最严重的区域位于③-D轴底层柱底部;而此时③-B轴底层柱上端及节点区内4根受压纵筋均已屈服,最大von Mises应力为328.2 MPa。
(3) 计算的纵筋最大屈服区域出现顺序(③→②)与试验框架退出工作的顺序(③→②)一致;计算的③-B柱上端纵筋屈服现象与试验时的破坏较吻合。
图6和图7所示为加载历史中第12和14加载步时框架箍筋的应力变化云图。从图6和图7可见:
在第12加载步时,结构首次出现箍筋屈服,主要位于③-B柱底层节点域内,最大von Mises应力为257.4 MPa。
在第14加载步时,结构中屈服箍筋主要位于③轴框架底层柱底部、顶部及顶部节点域内,最大von Mises应力为266.3 MPa,此时,③-B柱上端箍筋也已屈服,最大Mises应力为259.1 MPa。
比较框架纵筋、箍筋的屈服顺序不难发现:试验框架底层柱纵筋最先屈服,纵筋屈服后不久,则相应位置处的箍筋也很快进入屈服状态;当第14加载步结构达到极限承载力时刻,③轴框架底层柱上、下端的纵筋和箍筋均已进入屈服状态。究其原因,主要是框架柱的配箍不足,导致试验框架的延性发展受到限制,可见试验框架不能满足“强柱弱梁”、“强剪弱弯”、“强节点弱构件”的抗震设计原则。
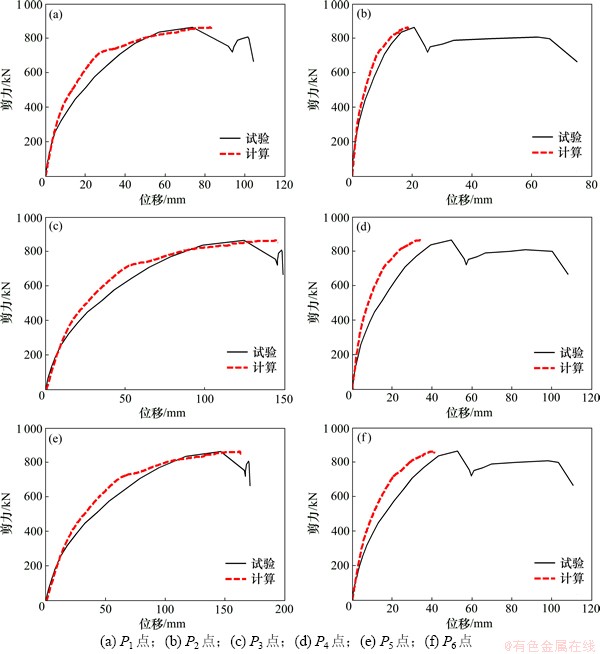
图3 试验框架荷载-位移曲线
Fig. 3 Load-displacement curves of the testing frame
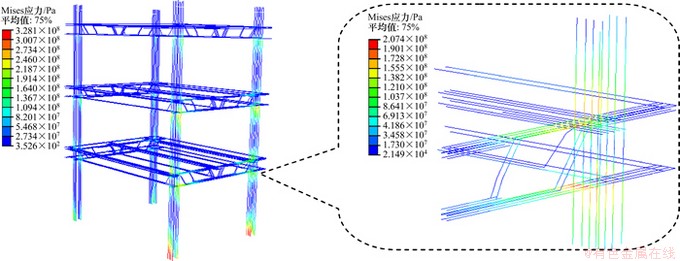
图4 第11加载步纵筋应力
Fig. 4 Stress of longitudinal rebar in 11th load step
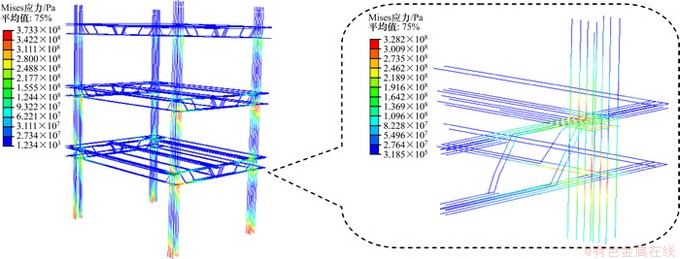
图5 第14加载步纵筋应力
Fig. 5 Stress of longitudinal rebar in 14th load step
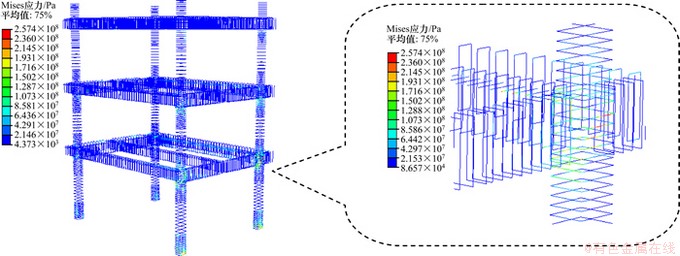
图6 第12加载步箍筋应力
Fig. 6 Stress of stirrup rebar in 12th load step
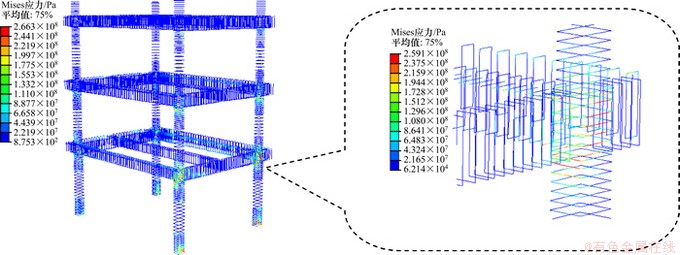
图7 第14加载步箍筋应力
Fig. 7 Stress of stirrup rebar in 14th load step
4.2 损伤分析
分别沿③和②轴线剖分框架,提取混凝土受拉损伤变量TDAMAGE,得到两榀框架梁、柱内部最终损伤情况,如图8所示。从图8可知:框架的损伤呈“上轻下重”的分布特征,主要集中在框架的底层和二层;柱的损伤较梁严重,且损伤主要集中在框架的底层柱;由于外砖墙的参与作用,使得③轴框架较②轴框架损伤严重。从损伤分布结果对比看,与试验观察现象较吻合。
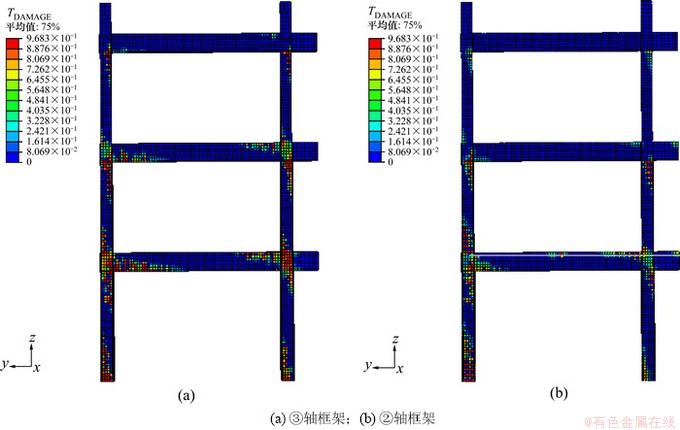
图8 第14加载步混凝土损伤分布
Fig. 8 Damage distribution of concrete in 14th load step
5 构件抗剪承载力
通过关键词*Section Print,从实体单元模型中提取用户自定义截面处的混凝土应力积分效果-轴力、剪力等。由于此处的截面内力是基于实体单元积分点的应力状态,考虑它们之间的耦合作用,所以较一维梁单元计算结果有更高的计算精度。首先,根据底层框架柱截面配筋情况,按偏压柱正截面的抗弯承载力计算柱的抗剪承载力,取底层③-B柱第11加载步时的轴力,按下式计算:
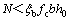 (7)
(7)
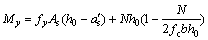 (8)
(8)
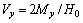 (9)
(9)
通过计算可得:纵筋屈服时,相应的剪力为129.73 kN。通过钢筋的应力分析得知,第11加载步时,框架柱底层首先出现纵筋屈服;在第14加载步时,底层框架柱端纵筋和箍筋均已出现屈服。
提取每个加载步下数值计算得到的加载方向底层框架柱剪力需求,并与分别按我国混凝土结构设计规范(GB 50011—2010)[22]、美国(ACI318—08)[23]、欧洲规范(Eurocode 8)[24]及新西兰规范(NZS3101)[25]规范的框架柱塑性铰区抗剪承载力计算结果绘在同一图中,如图9和图10所示。从图9和图10可见:
(1) 中国、美国规范公式对试验框架柱的抗剪承载力估计过高,因而偏于不安全;而欧洲、新西兰规范计算结果显示试验框架柱在塑性发展阶段会发生剪切破坏。
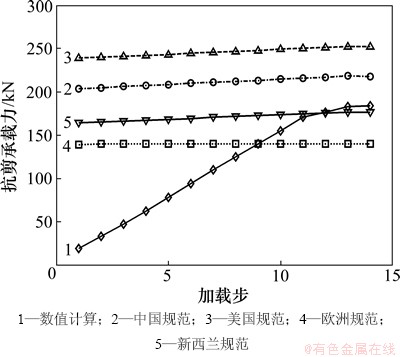
图9 ③-B柱抗剪承载力
Fig. 9 Shear strength of column ③-B
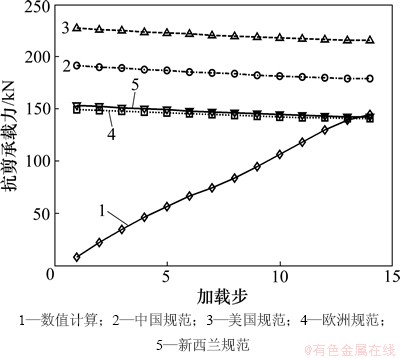
图10 ③-D柱抗剪承载力
Fig. 10 Shear strength of column ③-D
(2) 各国规范关于框架柱抗剪承载力计算结果的离散性较大,并且在处理塑性铰区发展与抗剪承载力退化关系时缺乏定量的指标,仅仅是给出不同延性要求下的临界值。框架柱弯曲屈服以后,在要求的变形能力(延性)范围内是否会发生剪切破坏问题值得深入研究。
6 结论
(1) 精细化模型较好地模拟了剪切破坏发生前试验框架的荷载-位移曲线。
(2) 试验框架的破坏模式是底层框架柱发生弯-剪破坏。首先,试验框架底层柱上端部纵筋屈服,此时框架柱的变形以弯曲变形为主;随着柱端受拉区混凝土不断开展,由于框架柱端箍筋不足,箍筋很快发生屈服,框架柱的弯曲延性发展受到限制,最终导致剪切破坏的发生。
(3) 各主要国家规范关于框架柱抗剪承载力计算结果的离散性较大,直接基于构件层次判断剪切破坏的发生可能存在一定的误差。
(4) 鉴于精细有限元模型模拟整体结构的计算工作量和收敛性问题,建立可靠的既有结构简化分析模型是下一步研究的重点。
参考文献:
[1] 江文卿, 邱聪智, 萧辅沛, 等. 花莲县新城国中校舍现场单向推覆试验[R]. 台湾, 中国: 国家地震工程研究中心, 2008: 1-65.
JIANG Wenqing, QIU Congzhi, XIAO Fupei, et al. In-situ pushover test of school building structure in Sin-Chen junior high school[R]. Taiwan, China: National Center for Research on Earthquake Engineering, 2008: 1-65.
[2] 江文卿, 邱聪智, 萧辅沛, 等. 云林县口湖国小校舍现场推覆试验[R]. 台湾, 中国: 国家地震工程研究中心, 2008: 1-43.
JIANG Wenqing, QIU Congzhi, XIAO Fupei, et al. In-situ pushover test of school building structure in Kao-Hu elematary school[R]. Taiwan, China: National Center for Research on Earthquake Engineering, 2008: 1-43.
[3] Ko Yungyen, Chen Chenghsing. Soil-structure interaction effects observed in the in situ forced vibration and pushover tests of school buildings in Taiwan and their modeling considering the foundation flexibility[J]. Earthquake Engineering and Structural Dynamics, 2010, 39(9): 945-966.
[4] Corte G D, Fiorino L, Mazzolani F M. Lateral-loading tests on a RC building including masonry infill panels with and without FRP strengthening[J]. Journal of Materials in Civil Engineering, 2008, 20(6): 419-431.
[5] Sharma A, Reddy G R, Vaze K K, et al. Pushover experiment and analysis of a full scale non-seismically detailed RC structure[J]. Engineering Structures, 2013, 46(1): 218-233.
[6] 田颖, 钱稼茹, 刘凤阁. 在用RC框架结构基于位移的抗震性能评估[J]. 建筑结构, 2001, 31(1): 53-56, 59.
TIAN Ying, QIAN Jiaru, LIU Fengge. Displacement-based seismic behavior evaluation for existing RC frame structures[J]. Building Structure, 2001, 31(1): 53-56, 59.
[7] 黄超, 季静, 韩小雷, 等. 基于性能的既有钢筋混凝土建筑结构抗震评估与加固技术研究[J]. 地震工程与工程振动, 2007, 27(5): 72-79.
HUANG Chao, JI Jing, HAN Xiaolei, et al. Research on performance-based seismic evaluation and strengthening for existing reinforced concrete structures[J]. Journal of Earthquake Engineering and Engineering Vibration, 2007, 27(5): 72-79.
[8] Kreslin M, Fajfar P. Seismic evaluation of an existing complex RC building[J]. Bulletin of Earthquake Engineering, 2010, 8(2): 363-385.
[9] 雷拓, 吕西林, 钱江, 等. 既有钢筋混凝土框架原位推覆试验研究[J]. 建筑结构学报, 2009, 30(5): 23-30.
LEI Tuo, L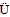 Xilin, QIAN Jiang, et al. In-situ pushover test of an existing reinforced concrete frame[J]. Journal of Building Structures, 2009, 30(5): 23-30.
Xilin, QIAN Jiang, et al. In-situ pushover test of an existing reinforced concrete frame[J]. Journal of Building Structures, 2009, 30(5): 23-30.
[10] 孙治国, 王东升, 李宏男, 等. 汶川地震钢筋混凝土框架震害及震后修复建议[J]. 自然灾害学报, 2010, 19(4): 114-123.
SUN Zhiguo, WANG Dongsheng, LI Hongnan, et al. Damage investigation of RC frames in Wenchuan earthquake and suggestions for post-earthquake rehabilitation[J]. Journal of Natural Disasters, 2010, 19(4): 114-123.
[11] GB 50011—2010, 建筑抗震设计规范[S].
GB 50011—2010, Code for seismic design of buildings[S].
[12] Lee J, Fenves G L. A plastic-damage model for cyclic loading of concrete structures[J]. J Eng Mechanics, 1998, 124(8): 892-900.
[13] GB 50010—2002, 混凝土结构设计规范[S].
GB 50010—2002, Code for design of concrete structures[S].
[14] 江见鲸, 陆新征, 叶列平. 混凝土结构有限元分析[M]. 北京: 清华大学出版社, 2005: 50-52.
JIANG Jianjing, LU Xinzheng, YE Lieping. Nonlinear finite element analysis of concrete structures[M]. Beijing: Tsinghua University Press, 2005: 50-52.
[15] 张劲, 王庆扬, 胡守营, 等. ABAQUS混凝土损伤塑性模型参数验证[J]. 建筑结构, 2008, 38(8): 127-130.
ZHANG Jin, WANG Qingyang, HU Shouying, et al. Parameters verification of concrete damaged plastic model of ABAQUS[J]. Building Structure, 2008, 38(8): 127-130.
[16] 李英民, 韩军, 刘立平. ANSYS在砌体结构非线性有限元分析中的应用研究[J]. 重庆建筑大学学报, 2006, 28(5): 90-96, 105.
LI Yingmin, HAN Jun, LIU Liping. Application of ANSYS to finite element analysis for nonlinear masonry structures[J]. Journal of Chongqing Jianzhu University, 2006, 28(5): 90-96, 105.
[17] Zucchini A, Lourenco P B. A micro-mechanical homogenisation model for masonry: Application to shear walls[J]. International Journal of Solids and Structures, 2009, 46(3): 871-886.
[18] 刘桂秋, 施楚贤, 刘一彪. 砌体及砌体材料弹性模量取值的研究[J]. 湖南大学学报(自然科学版), 2008, 35(4): 29-32.
LIU Guiqiu, SHI Chuxian, LIU Yibiao. Analyses of the elastic modulus values of masonry[J]. Journal of Hunan University (Natural Sciences), 2008, 35(4): 29-32.
[19]  P B. Analysis of masonry structures with interface elements: Theory and applications[R]. Delft: Faculty of Civil Engineering, Delft University of Technology. 1994: 1-80.
P B. Analysis of masonry structures with interface elements: Theory and applications[R]. Delft: Faculty of Civil Engineering, Delft University of Technology. 1994: 1-80.
[20] Stavridis A, Shing P B. Finite element modeling of nonlinear behavior of masonry-infilled RC frames[J]. Journal of Structural Engineering, 2010, 136(3): 285-296.
[21] 戴绍斌, 余欢, 黄俊. 填充墙与钢框架协同工作性能非线性分析[J]. 地震工程与工程振动, 2005, 25(3): 24-28.
DAI Shaobin, YU Huan, HUANG Jun. Non-linear analysis of coordinated working performance between infilled wall and steel frame[J]. Journal of Earthquake Engineering and Engineering Vibration, 2005, 25(3): 24-28.
[22] GB 50010—2010, 混凝土结构设计规范[S].
GB 50010—2010, Code for design of concrete structures[S].
[23] ACI 318—08. Building code requirements for structural concrete and commentary[S].
[24] Eurocode 8. Design provisions for earthquake resistance of structures[S].
[25] NZS3101, Part 1: The design of concrete structures[S].
(编辑 邓履翔)
收稿日期:2012-12-15;修回日期:2013-04-06
基金项目:国家自然科学基金资助项目(51278428);中国博士后科学基金资助项目(2012M511957)
通信作者:雷拓(1973-),男,陕西岐山人,博士,从事工程结构抗震及数值计算方面研究;电话:18710379516;E-mail:leituo616@163.com