DOI: 10.11817/j.issn.1672-7207.2017.04.024

地铁盾构近距离后行洞施工对先行洞影响的力学效应

刘代国，左昌群，唐霞，丁少林，陈建平

(中国地质大学(武汉) 工程学院，湖北 武汉，430074)

摘要：为揭示苏州地铁4号线区间隧道盾构近距离施工双洞之间的影响，采用数值计算和现场监测相结合的手段，获得后行洞施工条件下引起的先行洞附加应力及变形变化规律。研究结果表明：后行洞近距离施工会引起先行洞管片的二次附加应力，且在三维方向均有作用；其中径向附加应力主要呈受压状态，环向附加应力主要呈受拉状态，轴向附加应力由受压状态转化为受拉状态，且附加应力随着后行洞盾构的掘进逐渐增大并趋于稳定状态；由后行洞施工引起的径向附加应力最大约为0.028 MPa，环向附加应力最大约为0.270 MPa，轴向附加应力最大为0.700 MPa；管片及地层变形受土仓压力及注浆压力的影响明显，盾构连续施工过程中先行洞管片整体变形较大，最大变形约为6 mm；地层由隆起逐渐转为沉降，最大隆起量约为1.45 mm，随着盾构的远离，地表沉降逐渐增大，最大达14 mm左右；结合相关施工经验，后行洞施工对先行洞的影响处于可接受范围内，能保障隧道施工和结构受力稳定。

关键词：盾构隧道；盾构管片；附加应力；地层变形；土仓压力

中图分类号：TU94             文献标志码：A         文章编号：1672-7207(2017)04-1027-08

Mechanical effects of adjacent metro shield construction of the first hole on the second hole

LIU Daiguo, ZUO Changqun, TANG Xia, DING Shaolin, CHEN Jianping

(Faculty of Engineering, China University of Geosciences, Wuhan 430074, China)

Abstract: To reveal the impacts between double holes of Suzhou Metro Line 4 adjacent tunnel shield construction, the change laws of deformation and additional stress of the first hole were obtained by using the combination of numerical calculation and field monitoring method under the construction of the second hole. The results show that adjacent construction of the second hole can cause additional secondary stress to the first hole segment in three dimensions. Among them the radial additional stress is mainly in a state of compression, the circumferential additional stress is mainly in tension state, the axial additional stresses change from compressed state to a state of tension and three kinds of stresses gradually increase and stabilize with shield tunneling of the second hole. The maximum radial additional stress caused by the construction of the second hole is about 0.028 MPa, the maximum circumferential additional stress is about 0.270 MPa, and the maximum axial additional stress is about 0.700 MPa. The deformation of segment and ground soil is affected by the soil pressure and grouting pressure significantly. The overall deformation of segment of the first hole is larger during the shield continuous construction process and the maximum deformation is about 6 mm. The ground surface changes from uplift to settlement gradually and the maximum uplift is about 1.45 mm. The surface subsidence value is bigger with the shield tunneling away and the maximum value is about 14 mm. Combined with relevant experience in construction, the impact of construction of the second hole on the first hole is acceptable, which can guarantee the stability of the structure stability and the tunnel construction.

Key words: shield tunnel; shield segment; additional stress; stratum deformation; chamber earth pressure

随着我国城市地铁建设进入快速发展时期，盾构法施工因具有对周围环境影响小、施工速度快、工程质量优良、施工安全环保等优势，在城市地铁建设中得到了广泛应用。受地上或者地下空间的影响，盾构隧道不可避免地会形成近距离施工状况^[1-3]，在近距离施工条件下，先行洞会再次受到后行洞施工的影响，因此，研究近距离施工条件下后行洞施工对先行洞受力及变形的影响规律对隧道安全施工具有重要意义。目前人们对近距离盾构施工研究的成果较多，陈先国等^[4]针对近距离双孔平行隧道，采用二维有限元分析不同开挖方法管片弯矩图，探讨了第2孔隧道的修建对已建的第1孔隧道拱顶沉降的影响；王明年等^[5]用位移变化速率准则对盾构隧道重叠段进行了纵向近接分区；张海波等^[6]对近距离叠交情况下后建隧道盾构施工引起老隧道衬砌的应力和变形进行了模拟；白海卫等^[7]推导了正交下穿施工条件下既有隧道极限沉降变形公式，对其进行了安全评价；何川等^[8]采用模型试验和有限元分析探讨了隧道净距，顶推力等因素对已建平行隧道的变形和附加内力变化规律。通过对上述研究成果的调研发现，在管片受力方面研究的内容较变形研究的少，并且在管片受力方面主要着重于管片的整体受力状况，而在实际情况中管片处于三向受力状态，在径向、环向和轴向均表现出不同的受力状态。为确保近距离条件下盾构的正常施工需要对管片不同方向的受力情况进行及时掌握和了解，这就使得对相关问题的研究成为目前研究的重点和难点问题。为此，本文作者以苏州地铁4号线春申湖路站—阳澄湖路站盾构区间为研究对象，结合有限元数值模拟和现场监测手段，对近距离后行隧道施工条件下地表变形规律及先行隧道管片受力及变形变化规律进行研究，较全面地揭示近接施工条件下先行洞结构受力变形的综合力学效应，研究结论可为保障施工安全和掘进效率提供参考依据。

1  工程背景

1.1  工程概况

苏州市轨道交通4号线(主线)总体呈南北走向，春申湖路站—阳澄湖路站区间范围为测设里程右CK4+188.763~右CK5+447.142，全长1 258.379 m，为双向隧道，隧道中心距离10.00~15.50 m，隧道有效净距为3.8~9.3 m。盾构施工平面图见图1。

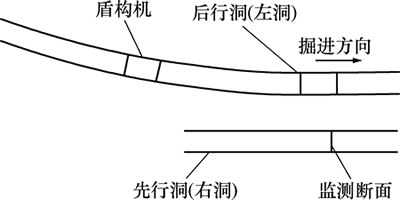
图1  盾构施工平面图

Fig. 1  Shield construction plan

1.2  施工方案

区间采用盾构法施工，采用2台土压平衡式盾构机向前推进，盾构直径为6.34 m，隧道衬砌采用C55预制钢筋混凝土管片，管片厚度为0.35 m，隧道外径为6.2 m，内径为5.5 m。为减小对土体的扰动，右洞较左洞早施工2月。

1.3  工程地质条件

隧道区间以第四系沉积地层为主，地下水位高，湖相沉积层厚。按其成因类型、岩性和工程性能依次为：素填土、湖相沉积粉质黏土、粉土层。区间地面标高一般在1.79~5.64 m之间，地势较平坦，局部桥梁部位稍有起伏。图2所示为隧道所处的地层图，表1所示为土体物理力学参数，盾构隧道处于④₁粉质黏土层中。

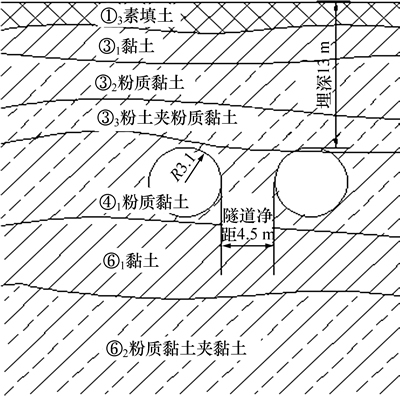
图2  地层剖面图

Fig. 2  Geological profile

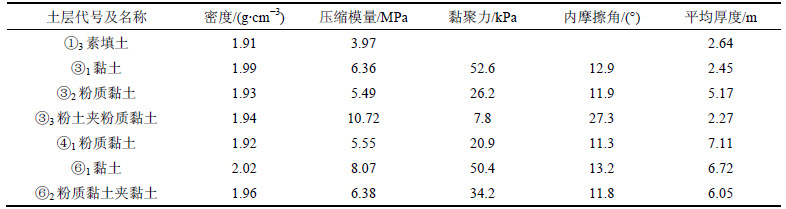
表1  土体物理力学参数

Table 1  Physical and mechanical parameters of soils

2  近接段后行洞对先行洞影响的数值分析

2.1  计算模型建立

采用有限元分析软件ABAQUS进行计算，以CK4+942~CK5+014段的CK4+978断面作为研究对象；此断面隧道埋深为13 m，隧道净距为4.5 m。取隧道外边界与模型边界距离为20 m，计算模型长×宽×高为57.3 m×72.0 m×40.0 m，计算模型如图3所示。盾构沿x方向掘进，掘进长度为72 m。考虑到衬砌接头对衬砌结构刚度的影响，将衬砌管片刚度折减0.15，得到管片的弹性模量为30 GPa，泊松比为0.2，管片宽度为1.2 m。由于土体、浆体向盾尾空隙充填情况以及隧道壁面受扰动程度和范围难以进行量化，因此，将它们等效为均质、等厚、弹性的等代层^[9-10]，根据文献[10]取等代层厚度为0.1 m，弹性模量为3 MPa，泊松比为0.2，盾构机、等代层和衬砌看作为弹性材料，土体为弹塑性材料，屈服准则采用Drucker-Prager准则。土体、盾构机、等代层及衬砌单元类型均为C3D8。

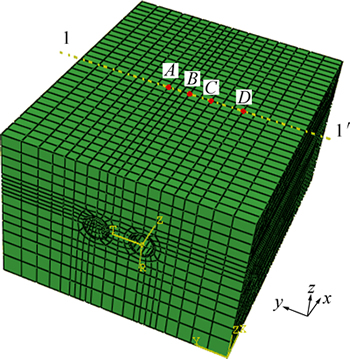
图3  三维有限元模型

Fig. 3  3D FEM model

2.2  计算工况条件

在实际施工中，每次掘进1.2 m，为简化模型，在模拟过程中，每次掘进2.4 m，将管片共分为30环。采用刚度迁移法^[11]模拟盾构的施工过程。为减小边界效应^[12]的影响，盾构机距端部5环开始推进，此时激活衬砌单元和等代层单元。将接下来3环土体挖去，激活盾构单元并施加土仓压力维持工作面稳定，进而模拟盾构动态掘进过程，每步开挖1环，时间步长设为1，共掘进27环，消耗总时间步长为22。盾构推进模拟图^[13-14]如图4所示，其主要推进步见表2，并依次循环下去直至隧道贯通。根据盾构推进记录，土仓压力设定范围为0.17~0.21 MPa，注浆压力取值范围为0.25~0.35 MPa，本文模拟中取土仓压力为0.18 MPa，注浆压力为0.3 MPa。

表2  计算步骤

Table 2  Calculation steps

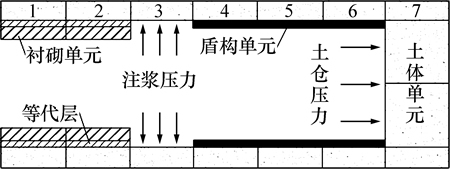
图4  有限元模拟过程图

Fig. 4  FEA simulation process

2.3  监测工况

为和实际情况相吻合，选取模型中部第15环作为分析断面，选取管片外环拱顶、拱底、左拱腰及右拱腰进行径向应力监测，即埋设压力盒位置处。选取与后行洞(左洞)近接处，即管片内环水平位置、±45°位置处进行环向应力和轴向应力监测，即安装应变计位置处，应力监测点具体布置如图5所示。另外，选取监测断面正上方地表处1-1’测线及测线上的A，B，C和D共4点作为研究对象，A~Ｄ所处位置依次为左洞拱顶正上方、两隧道中轴线处、右洞拱顶正上方及右洞拱顶向右约7 m处，分析盾构掘进过程中其变形规律，地表变形监测点布置如图3所示。

图5  监测点布置图

Fig. 5  Monitoring points layout

2.4  计算结果分析

2.4.1  附加应力分析

图6所示为后行洞施工引起先行洞分析断面处径向附加应力变化时程曲线。后行洞施工引起先行洞管片所受的径向附加应力整体上呈增大的趋势，在推进时间步为11时，后行洞工作面到达分析断面处，在到达之前，拱顶、拱底处径向附加应力值向负方向增大，表明其相对初始径向应力有减小的趋势，减小量为3 kPa；右拱腰处呈现直线增加的趋势，而在左拱腰处，在盾构到达分析断面之前基本上保持不变；随着盾构机的通过其增加速率陡增，最大径向附加应力为28 kPa，受盾构开挖影响较大。随着盾构机的远离，监测点的径向附加应力基本保持不变。

图6  径向附加应力时程曲线

Fig. 6  Radial additional stress-time curve

图7所示为后行洞施工引起先行洞管片环向附加应力变化时程曲线。从图7可见：环向附加应力总体上沿负方向增大，在土仓压力及注浆压力的作用下，对前方及周边土体产生挤压作用，使得先行洞管片内环受拉效应明显。盾构推进时间步为9即距离分析断面为2环之前，管片环向附加应力受盾构机影响较小，变化曲线基本保持水平；随着盾构机达到并穿过分析断面，其应力受盾构机影响较大，影响范围约为8环；随着盾构机的远离，分析断面环向附加应力受盾构机影响减小。对比3处监测点，水平位置处变化幅度最大，约为0.25 MPa，-45°位置处变化幅度最小，为9 kPa。

图7  环向附加应力时程曲线

Fig. 7  Circumferential additional stress-time curves

图8所示为后行洞施工引起先行洞管片轴向附加应力变化时程曲线。监测点处轴向附加应力有拉应力也有压应力，其中+45°位置和水平位置处变化规律较一致，相对-45°位置处，由受压状态转化为受拉状态存在一定的滞后性；在距离分析断面为1环附近，水平位置和+45°位置处压应力达到最大，在开挖结束时拉应力达到最大，变化幅度约为0.65 MPa；-45°位置处随着工作面远离分析断面6环时其拉应力达到最大，随着盾构机的继续掘进其拉应力有减小的趋势。

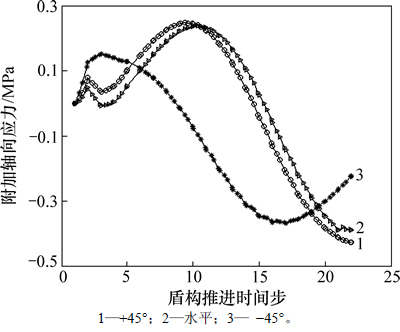
图8  轴向附加应力时程曲线

Fig. 8  Axial additional stress-time curves

2.4.2  变形分析

图9所示为后行隧道分析断面处管片拱腰处水平位移时程曲线。从图9可见：随着后行洞的施工，先行洞管片整体向右移动较大，左拱腰与右拱腰水平位移差值较小，表明其净收敛量较小；管片向右最大水平位移约为6 mm，而其净收敛量低于1 mm。

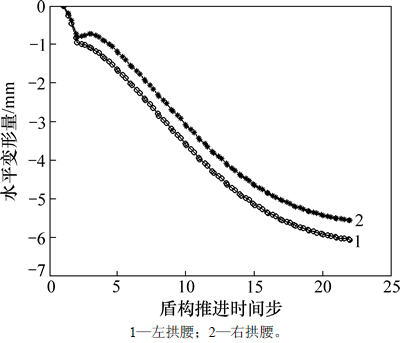
图9  管片水平位移图

Fig. 9  Horizontal displacement of segment

图10所示为横向监测线1-1’变形曲线图。从图10可见：在工作面到达监测断面之前，土体受土仓压力和注浆压力的挤压作用，地表变形表现为隆起现象，在到达监测断面时，地表隆起量最大，约为1.6 mm；随着盾构的继续掘进，受土仓压力和注浆压力的影响逐渐减小，地表变形表现为沉降现象，在盾构开挖结束时即开挖到27环时，地表沉降量最大，约为12.8 mm。

图10  地表沉降曲线

Fig. 10  Surface subsidence curves

图11所示为监测线1-1’上A，B，C和D共4点竖向位移时程曲线。从图11可见：在盾构机到达监测断面前，地表变形以隆起为主，在穿越过程中，地表沉降迅速增大，随后变形量趋于稳定状态；后行洞正上方A点处沉隆值最大，向着先行洞方向沉降逐渐减小，在D点处，变形曲线图近似平直线，受后行洞施工影响较小。

图11  监测点竖向位移时程曲线

Fig. 11  Vertical displacement-time curves of monitoring points

3  盾构近距离施工相互影响的现场监测分析

为研究近距离条件下后行洞施工对先行洞管片受力的影响，通过在先行洞管片上埋设压力盒和应变计的方式进行监测记录。当后行洞工作面距监测断面为50环时，记录此时的应力作为初始值，观察盾构在掘进过程中先行洞管片附加应力变化情况，盾构机实际掘进过程中每天6~12环，在累计时间为7 d时，后行洞工作面到达监测断面。

3.1  附加应力监测分析

图12所示为实际监测中管片径向附加应力变化时程曲线。从图12可见：实际监测得到的附加径向力变化规律与模拟得到的较为类似；随着工作面的到达及远离，径向附加应力逐渐变大并趋于稳定，在左拱腰处增量最大，在拱底处增量最小。模拟结果中，左拱腰、拱顶、拱底和右拱腰达到稳定状态时径向附加应力分别为28， 11，7和9 kPa，在实际监测中，相应值约为23，10，4和12 kPa，右拱腰处影响程度次于左拱腰处影响程度。

图12  径向附加应力监测曲线

Fig. 12  Monitoring curves of radial additional stress

图13所示为实际监测中管片环向附加应力变化时程曲线。从图13可见：后行洞施工引起先行洞水平位置处环向附加应力最大，-45°处最小；水平位置及+45°位置处应力随着盾构机的到达增量较大；随着盾构机远离监测断面约40环时，应力趋于稳定，而-45位置处随着后行洞施工应力变化值较小，趋于稳定较快；+45°、水平和-45°位置处环向附加应力稳定时应力分别为0.14，0.27和0.025 MPa，数值模拟结果中，相应应力为0.17，0.23和0.05 MPa，3处均处于受拉状态。

图14所示为实际监测中管片轴向附加应力变化时程曲线。从图14可见：随着后行洞的施工，在数值模拟和实际监测中先行洞管片+45°、水平位置处轴向附加应力均由压应力转化为拉应力，而-45°位置处在实际监测中则始终处于受拉状态。在实际监测中，3处应力状态在后行洞工作面到达监测断面时应力基本处于最大值；随后轴向附加应力趋于稳定状态。+45°，0°和-45°位置处轴向附加应力变化幅度约为0.6，0.7和0.4 MPa。在数值模拟结果中，在盾构穿越监测断面之后3点处应力达到最大并趋于稳定甚至减小，3处相应的变化幅度约为0.60，0.65和0.50 MPa。

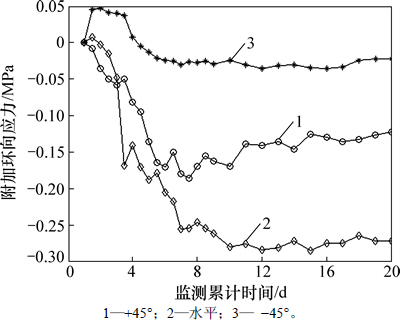
图13  环向附加应力监测曲线

Fig. 13  Monitoring curves of circumferential additional stress

图14  轴向附加应力监测曲线

Fig. 14  Monitoring curves of axial additional stress

3.2  地表变形监测分析

图15所示为后行洞施工过程中监测断面处地表变形曲线，图15中的中心距负值对应后行洞一侧，正值对应先行洞一侧，d为工作面距离监测断面的距离。盾构到达监测断面之前地表以隆起为主，隆起值为1.45 mm，较数值模拟得到的隆起值小。随着盾构穿过监测断面地表沉降逐渐增大，在后行洞上方地表沉降最大，当d=32 m时，地表最大沉降为14.42 mm。

图15  地表沉降监测曲线

Fig. 15  Monitoring curves of surface subsidence

4  盾构近距离施工后行洞对先行洞影响规律

在后行盾构隧道施工过程中，随着近接距离逐渐减小，周围土体受到因盾构机推进引起的开挖方向前方及盾构机周围的土压平衡力、界面摩擦阻力及盾尾注浆压力等力的作用。由于盾壳与地层之间的摩擦阻力作用，必然会产生1个滑动面。临近滑动面的土层中就会产生剪切应力，当盾构刚通过受剪切破坏的地层时，因受剪切而产生的拉应力导致土体立刻向盾构后的空隙移动。要保持盾构能与隧道轴线一致，在推进过程中盾构所经之处必须压缩一部分土体，松弛另一部分土体。压缩部分抵挡了盾构偏离，而松驰部分则带来了先行洞受力和位移的变化。

在实际监测中，径向、环向、轴向附加应力变化时程曲线可分为急剧变化阶段、波动阶段和稳定阶段，数值模拟结果中则可分为急剧变化阶段和稳定阶段。通过数值模拟和实际监测可以得到：盾构在即将穿越监测断面时，附加应力变化速率较大，在穿越之后附加应力达到最大值，随着盾构机的远离附加应力逐渐趋于稳定状态。受后行洞盾构施工的影响，管片左拱腰和右拱腰处径向应力增量值较其他监测点大。盾构切削挤压土体过程中，使得先行洞管片内环处于受拉状态，在管片内环处引起的环向附加应力和附加轴向应力沿负方向逐渐增大，其中在水平位置处影响最明显，在-45°位置处受盾构施工影响较弱。

由后行隧道盾构施工引起先行隧道管片径向最大附加应力为0.028 MPa，环向最大附加应力0.27 MPa，轴向最大附加应力为0.70 MPa。轴向附加应力和环向附加应力明显大于径向附加应力，说明在双孔平行隧道近距离施工条件下，盾构对土体的推挤力在先行隧道管片横断面上所产生的分力较小，在软黏土地层中，管片与土体之间存在较好的黏结性，盾构在纵向产生的较大的推挤力，使得管片轴向附加应力较大。因此，在近距离施工的软土地层中，对盾构土仓压力的控制更为重要。3种附加应力比盾构土仓压力小，对管片的安全使用影响很小，3种附加应力均处于合理范围之内。

5  结论

1) 在近距离施工条件下，后行洞盾构的土仓压力及注浆压力对前方及周边土体形成挤压作用，使得先行洞管片附加径向应力呈增大趋势，近接处管片内环环向附加应力呈受拉状态，而轴向附加应力由受压状态转化为受拉状态。随着盾构远离监测断面，管片受盾构施工的影响减小，3种附加应力基本上处于稳定状态。总体上，后行洞盾构施工对先行洞管片近接水平位置影响最大，对-45°位置处影响最小。

2) 先行洞管片整体水平位移较大，左拱腰处位移大于右拱腰处位移，受后行洞施工的影响，先行洞收敛值较小，低于1 mm。

3) 后行洞工作面到达监测断面之前，地表变形出现隆起现象，隆起值约为1.45 mm；随着盾构穿过监测断面，地表变形以沉降为主，且变形幅度较大，最大沉降量在后行洞上方，约为14.42 mm；随着工作面远离监测断面，地表沉降逐渐增大并趋于稳定。

参考文献：

[1] 陶连金, 孙斌, 李晓霖. 超近距离双孔并行盾构施工的相互影响分析[J]. 岩石力学与工程学报, 2009, 28(9): 1856-1862.

TAO Lianjin, SUN Bin, LI Xiaolin. Interaction analysis of double holes extremely close approaching parallel shield tunnels construction[J]. Chinese Journal of Rock Mechanics and Engineering, 2009, 28(9): 1856-1862.

[2] FANG Qian, ZHANG Dingli, LI Qianqian, et al. Effects of twin tunnels construction beneath existing shield-driven twin tunnels[J]. Tunnelling and Underground Space Technology, 2015, 45: 128-137.

[3] SHI Jiangwei, NG C W W, CHEN Yonghui. Three-dimensional numerical parametric study of the influence of basement excavation on existing tunnel[J]. Computers and Geotechnics, 2015, 63: 146-158.

[4] 陈先国, 高波. 地铁近距离平行隧道有限元数值模拟[J]. 岩石力学与工程学报, 2002, 21(9): 1330-1334.

CHEN Xianguo, GAO Bo. 2D FEM numerical simulation for closely-spaced parallel tunnels in metro[J]. Chinese Journal of Rock Mechanics and Engineering, 2002, 21(9): 1330-1334.

[5] 王明年, 张晓军, 苟明中, 等. 盾构隧道掘进全过程三维模拟方法及重叠段近接分区研究[J]. 岩土力学, 2012, 33(1): 273-279.

WANG Mingnian, ZHANG Xiaojun, GOU Mingzhong, et al. Method of three-dimensional simulation for shield tunneling process and study of adjacent partition of overlapped segment[J]. Rock and Soil Mechanics, 2012, 33(1): 273-279.

[6] 张海波, 殷宗泽, 朱俊高. 近距离叠交隧道盾构施工对老隧道影响的数值模拟[J]. 岩土力学, 2005, 26(2): 282-286.

ZHANG Haibo, YIN Zongze, ZHU Jungao. Numerical simulation of influence of new tunnel on short distance overlapped old tunnel during shield tunneling[J]. Rock and Soil Mechanics, 2005, 26(2): 282-286.

[7] 白海卫, 何海健, 李玲. 正交下穿施工对上部既有隧道安全的影响研究[J]. 地下空间与工程学报, 2014, 10(2): 434-440.

BAI Haiwei, HE Haijian, LI Ling. Study on longitudinal deformation and internal forces of upper existing metro tunnel caused by undercrossing tunneling[J]. Chinese Journal of Underground Space and Engineering, 2014, 10(2): 434-440.

[8] 何川, 苏宗贤, 曾东洋. 盾构隧道施工对已建平行隧道变形和附加内力的影响研究[J]. 岩石力学与工程学报, 2007, 26(10): 2063-2069.

HE Chuan, SU Zongxian, ZENG Dongyang. Research on influence of shield tunnel construction on deformation and secondary inner force of constructed parallel tunnel[J]. Chinese Journal of Rock Mechanics and Engineering, 2007, 26(10): 2063-2069.

[9] 张云, 殷宗泽, 徐永福. 盾构法隧道引起的地表变形分析[J]. 岩石力学与工程学报, 2002, 21(3): 388-392.

ZHANG Yun, YIN Zongze, XU Yongfu. Analysis on three-dimensional ground surface deformations due to shield tunnel[J]. Chinese Journal of Rock Mechanics and Engineering, 2002, 21(3): 388-392.

[10] 陈卫忠, 伍国军, 贾善坡. ABAQUS在隧道及地下工程中的应用[M]. 北京: 中国水利水电出版社, 2010: 87-91.

CHEN Weizhong, WU Guojun, JIA Shanpo. Application of ABAQUS in tunnel and underground engineering[M]. Beijing: China Water Power Press, 2010: 87-91.

[11] 王敏强, 陈胜宏. 盾构推进隧道结构三维非线性有限元仿真[J]. 岩石力学与工程学报, 2002, 21(2): 228-232.

WANG Minqiang, CHEN Shenghong. Three-dimensional nonlinear finite element simulation of tunnel structure for moving-forward shield[J]. Chinese Journal of Rock Mechanics and Engineering, 2002, 21(2): 228-232.

[12] 贾善坡. Boom Clay泥岩渗流应力损伤耦合流变模型、参数反演与工程应用[D]. 武汉: 中国科学院研究生院(武汉岩土力学研究所), 2009: 129-142.

JIA Shanpo. Hydro-mechanical coupled creep damage constitutive model of Boom clay, back analysis of model parameters and its engineering application[D]. Wuhan: Graduate School of Chinese Academy of Sciences (Wuhan Institute of Rock and Soil Mechanics), 2009: 129-142.

[13] 林志, 朱合华, 夏才初. 双线盾构隧道施工过程相互影响的数值研究[J]. 地下空间与工程学报, 2009, 5(1): 85-89.

LIN Zhi, ZHU Hehua, XIA Caichu. Numerical modeling study on interaction between twin shields tunneling[J]. Chinese Journal of Underground Space and Engineering, 2009, 5(1): 85-89.

[14] 李磊, 张孟喜, 吴惠明, 等. 近距离多线叠交盾构施工对既有隧道变形的影响研究[J]. 岩土工程学报, 2014, 36(6): 1036-1043.

LI Lei, ZHANG Mengxi, WU Huiming, et al. Influence of short-distance multi-line overlapped shield tunnelling on deformation of existing tunnels[J]. Chinese Journal of Geotechnical Engineering, 2014, 36(6): 1036-1043.

(编辑  杨幼平)

收稿日期：2016-04-06；修回日期：2016-06-15

基金项目(Foundation item)：国家自然科学基金资助项目(41202201，51379194)；中央高校基本科研业务费专项资金资助项目(CUGL110215) (Projects (41202201, 51379194) supported by the National Natural Science Foundation of China; Project (CUGL110215) supported by the Fundamental Research Funds for the Central Universities)

通信作者：左昌群，博士，讲师，从事地下建筑工程围岩-结构稳定性分析及灾害预测预报研究；E-mail：helenzz@126.com