文章编号：1004-0609(2011)02-0371-06

机械合金化法制备Cu-Nb合金过程中的形变孪生特性

雷若姗¹，汪明朴¹，郭明星²，李  周¹，魏海根¹

(1. 中南大学 材料科学与工程学院，长沙 410083；

2. Institute of Materials Science, Lausanne Federal Institute of Technology, Lausanne CH-1015, Switzerland)

摘  要：采用机械合金化法制备纳米Cu-10%Nb合金，通过显微硬度测量以及高分辨透射电镜观察，对该合金粉末在室温球磨过程中的微观结构演变和形变孪生特性进行研究；利用局部应力集中模型分析形变孪晶的形核机制。结果表明：随着球磨时间的增加，该合金硬度(HV)不断升高，球磨120 h后可达4.8 GPa；该合金在球磨初期以位错胞结构为主；球磨50 h后，Cu平均晶粒尺寸减小至约50 nm，部分区域出现纳米形变孪晶；继续增加球磨时间，孪晶数量增加，孪晶界强化效果显著；由于孪生将促进纳米晶粒的进一步细化，球磨120 h后，纳米晶尺寸减小到20 nm以下。

关键词：Cu-Nb合金；机械合金化；形变孪晶；孪晶界强化；纳米材料

中图分类号：TG146.1　　     文献标志码：A

Deformation twinning characteristic of mechanically alloyed Cu-Nb alloy powders

LEI Ruo-shan¹, WANG Ming-pu¹, GUO Ming-xing², LI Zhou¹, WEI Hai-gen¹

(1. School of Materials Science and Engineering, Central South University, Changsha 410083, China;

2. Institute of Materials Science, Lausanne Federal Institute of Technology, Lausanne CH-1015, Switzerland)

Abstract: The microstructure evolution and deformation twinning characteristics of nanocrystalline Cu-10%Nb alloy during mechanical alloying (MA) were investigated by microhardness measurements, transmission electron microscopy (TEM) and high resolution TEM (HRTEM) observation. A local stress concentration model was proposed to explain the deformation twin nucleation mechanism of Cu-Nb alloy. The results show that the Vickers microhardness of the powders increases gradually with the increase of milling time, and reaches 4.8 GPa after 120 h milling. The main structure of the powders is the dislocation cells in the initial milling. After 50 h milling, the average Cu grain size decreases to about 50 nm, and nano-deformation twins begin to form in some regions. With the continued increase of the milling time, the number of twin increases, and the twin boundary strengthening enhances accordingly. Due to the deformation twinning will contribute to further refine the nano-grains, after 120 h milling, the nano-crystalline size decreases to below 20 nm.

Key words: Cu-Nb alloy; mechanical alloying; deformation twinning; twin boundary strengthening; nanostructured material

机械合金化(MA)制备的纳米晶Cu-Nb合金是一种兼具有高强、高导以及良好抗高温软化性能的先进复合材料^[1-5]。虽然大多数研究结果均表明，该合金优异的综合性能主要是因为MA后强固溶于Cu基体中的Nb将在后续热处理过程中均匀弥散的析出，从而对位错和晶界起到强烈的钉扎作用^[2]，但是，关于MA过程中的强固溶机制以及晶粒细化过程等方面的研究却很不深入。

对于传统粗晶金属，特别是中、高层错能面心立方金属，如Al和Cu等，其塑性形变主要通过位错滑移实现，很少观察到形变孪晶^[6]。然而，BLEWITT   等^[7]报道，粗晶Cu在低温和/或高应变速率下(约为 10³ s^-1)变形时，可能发生形变孪生。粗晶态面心立方金属发生形变孪生一般用极轴机制(Pole mechanism)解释^[8]，即形变孪生是通过棱柱位错分解成不全位错的方式形核，而后通过Shockley不全位错呈螺旋式不断转动到相邻(111)面长大，从而形成孪生片层区。近几年来的分子动力学(MD)模拟及实验研究证明中、高层错能纳米晶材料中也存在形变孪晶^[9-13]。如，LIAO等^[11]在纳米Cu的高压扭转实验中，发现纳米Cu在室温和低的应变速率下变形时发生显著的形变孪生。粗晶和纳米晶Cu在一定条件下均会发生形变孪生，然而当存在第二组元Nb元素之后，在MA过程中，Cu晶粒的细化过程，是否也会发生形变孪生以及相应的孪生机制，目前并未发现相关报道。而这方面的研究不仅对于更好的理解形变孪生机制有积极的推动作用，而且对于制备超高强纳米晶Cu-Nb合金的工艺优化以及组织控制等也具有重要的指导作用。因此，本文作者拟对Cu-10%Nb合金在MA过程中粉末微观结构演变、晶粒细化机制及形变孪生行为进行系统的研究。此外，为了更好地弄清这些行为之间的内在关系，本文作者还通过理论模型对形变孪晶形成机制进行系统深入地分析。

1  实验

将纯Cu粉(纯度＞99.8%，粒度＜100 ?m)和纯Nb粉(纯度＞99%，粒度<80 ?m)以含Nb量10%(质量分数)的配比混合后，与不锈钢球一同放入不锈钢钢罐中，在QM-1F型行星式球磨机上进行原始粉末的低速混料及高速球磨。球磨过程参数：球料比为14:1(质量比)，转速为300 r/min，在氩气保护下室温球磨120 h。分别对15、30、50、100、120 h球磨后的样品进行了硬度(HV)测量与透射显微组织观察。样品硬度(HV)在HVA-10A型小负荷维氏硬度计上测量，载荷为30 N，加载30 s。透射电镜(TEM)和高分辨电镜(HRTEM)观察在JEM-2100透射电镜上进行，操作电压为200 kV。透射电镜样品采用离子减薄法制备。

2  结果与讨论

2.1  球磨时间对粉末硬度(HV)的影响

图1所示为Cu-10%Nb合金粉末硬度(HV)随球磨时间的变化趋势。从图1中可以看出：随着球磨时间的增加，合金硬度(HV)升高较快；球磨120 h后，该合金粉末硬度(HV)高达4.8 GPa，几乎超过了目前所有铜合金的硬度。文献[5]表明，在相同球磨条件下，Cu-10%Nb合金球磨40 h后，大部分Nb原子已固溶于Cu基体内，纳米Cu晶粒细化及内应力增加速率逐渐变缓。但由图1可见，球磨40 h后，继续延长球磨时间，粉末硬度(HV)升高速率并未发生显著减缓。由此可知，当球磨时间超过40 h后，合金硬度(HV)的持续升高除了源于固溶强化、细晶强化和应变强化外，一定还存在另一种强化机制在起作用。后面的显微组织观察表明，球磨到后期，该合金Cu基体内会出现大量纳米尺寸的孪晶组织。以往研究发现，孪晶界与大角度晶界类似，也可以有效阻碍位错运动，提高材料强度^{[12, 14]}，而且其对硬度的贡献随着纳米孪晶数量的增加而快速增加，因此，即使当球磨时间超过100 h后，本研究的Cu-10%Nb合金的硬度(HV)仍在上升。

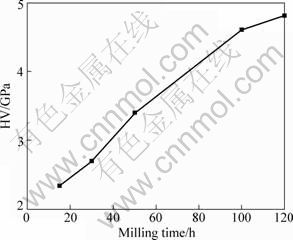
图1 　球磨时间对Cu-10%Nb合金粉末硬度的影响

Fig.1  Effect of milling time on microhardness of Cu-10%Nb alloy

2.2  微观结构分析

图2所示为Cu-10%Nb合金粉末经不同时间球磨后的TEM及HRTEM像。图2(a)所示为该合金粉末球磨15 h后的典型TEM显微组织。由图2(a)可见，球磨初期，Cu基体内形成了大量典型的位错胞组织，胞平均尺寸约为400 nm。对此区域进行选区衍射(见图2(a)中插图所示)发现，Cu基体的衍射斑点拉长，出现隐约多晶环，表明合金变形严重，位错胞之间存在一定的取向差。

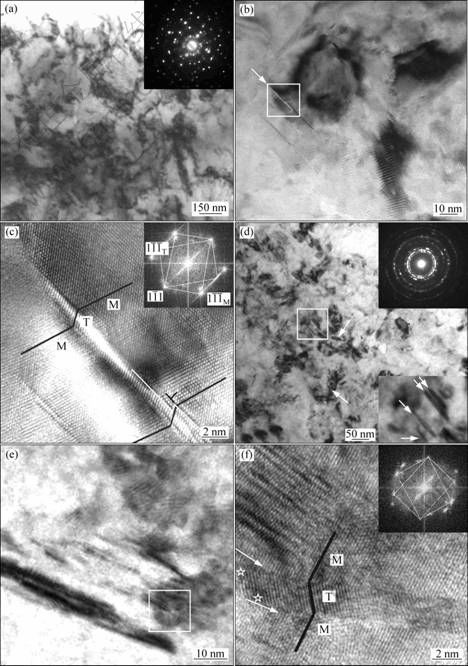
图2  Cu-10%Nb合金粉末不同时间球磨后的TEM和HRTEM显微组织照片

Fig.2  TEM and HRTEM images showing change in microstructure of Cu-10%Nb alloy with respect to milling time: (a) TEM image, 15 h; (b) TEM image, 50 h; (c) HRTEM image of select area mark in (b); (d) TEM image, 100 h; (e) TEM image, 120 h; (f) HRTEM image of select area mark in (e)

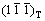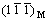图2(b)所示为该合金粉末球磨50 h后的TEM像。由图2(b)可见，粉末中形成了纳米晶和纳米片层状组织，Cu基体平均晶粒尺寸约为50 nm。图2(c)所示为图2(b)中白框区域对应的高分辨像。由图2(c)及其傅里叶变换图像(插图所示)可以清楚地看到，该片层结构为形变孪晶片层，孪晶面为(111)。此时，由于Cu晶粒尺寸较小，基体内独立的滑移系显著减少，滑移所需剪切应力开始高于孪生应力，因此，进一步滑移逐渐困难，从而出现如图2(b)所示的形变孪晶片层。仔细对比图2(b)和(c)可以看出，该孪晶片层由尺寸约为49 nm的纳米晶Cu晶界起源，并贯穿于整个纳米晶粒。同时，孪晶片层厚度不均匀，孪晶界上出现了两个原子层厚的孪晶台阶(白色箭头与折线标出)，但无多余半原子面，与(T代表孪晶；M代表Cu基体)依旧以孪晶界呈镜面对称，保持着严格的孪晶关系。因此，孪晶台阶是由位于台阶顶部，并且不改变孪晶关系的Shockley不全位错形成(黑色⊥所示)。在形变过程中，该Shockley不全位错沿孪晶界的运动将使得孪晶片层进一步变宽增厚^[15]。

图2(d)所示为该合金粉末球磨100 h后的TEM像。由图2(d)可见，Cu晶粒尺寸进一步减小到15~40 nm，在直径仅为500 nm区域内进行选区衍射(见图2(d)中右上插图所示)，衍射花样为连续多晶环，表明在此区域内晶粒尺寸显著细化。由该图中白框区域的放大图像可见(见图2(d)中右下插图所示)，在一宽约35 nm的Cu晶粒中，四片长度不等的形变孪晶在晶界处不均匀形核(黑色箭头标出)，有的孪晶片层贯穿整个晶粒，有的终止于晶内。同时，孪晶片层数量较球磨50 h后有所增加，且孪晶片层厚度增厚，但仍低于4 nm。

图2(e)所示为球磨120 h后的TEM像，图2(f)所示为图2(e)中白框区域对应的高分辨HRTEM像。由图2(e)和(f)可见，此时在尺寸约为20 nm的Cu亚晶内出现了纳米形变孪晶，黑色箭头所指处为孪晶界。同时，由于孪晶界形成的亚结构与晶界之间的互相作用，可能导致发生了不均匀孪生的亚晶界段出现形状的改变(见图2(f)中星号所标示)。

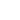
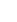根据上述不同时间球磨后Cu-10%Nb合金粉末微观结构的研究结果，其晶粒细化过程可描述如下：在球磨初期，Cu晶粒尺寸较大，晶体形变以位错滑移为主，形成位错胞结构(见图2(a))；随着球磨时间的延长，位错密度不断增大，晶粒不断得到细化，并出现大量纳米晶粒；在球磨后期，特别当Cu晶粒尺寸减小到15~50 nm后，全位错增殖与运动受到抑制；但由于晶粒尺寸仍大于10 nm，晶界滑移与晶粒旋转尚很难进行^[13]，此时，形变孪生开始成为协调塑性形变的重要方式(见图2(b)~(f))，并且，形变孪晶数量随球磨时间的增加而相应增多；通过形变孪生所形成的亚结构，纳米晶粒进一步被分割细化，晶体取向发生改变；另外，在晶界处形成的微孪晶也可能生长为新晶粒^[9]。最终，MA法制备的Cu-10%Nb合金同时出现超细纳米晶和纳米形变孪晶片层的微观结构特征。

2.3  Cu-10%Nb合金中形变孪晶的形成机制

通过上述TEM和HRTEM观察可知，Cu-Nb合金经长时间球磨后形成了纳米晶及纳米形变孪晶片层组织，其变化规律是孪晶首先在晶界处形核，续而不断扩展，甚至贯穿于整个晶粒，并且，孪晶数量随球磨时间的增加而增多。

众所周知，当晶粒尺寸下降到一定程度后，弗兰克-瑞德位错增殖机制不再适用，位错大多从晶界和晶界交叉点处产生，并迅速穿过晶粒，在另一边晶界处湮没，几乎无位错停留在晶内^[16]，因此，不能采用极轴机制分析Cu-10%Nb合金中形变孪晶的形成机制。由于当晶界和晶界交叉点处产生不全位错所需剪切应力低于全位错时，形变孪晶可通过不全位错的不断发射而产生^[10]，因此，可根据晶界处产生不全位错和全位错所需剪切应力的不同，对Cu-Nb合金形变孪生机制进行系统的分析。产生全位错所需的剪切应力(τ_s)可以表述为^[10]

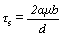                                  (1)

而产生不全位错所需的剪切应力(τ_p)为

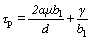                             (2)

式中：γ为层错能；μ为剪切模量；d为晶粒尺寸；b和b₁分别为全位错和不全位错的柏格斯矢量；参数α反映了位错特性(刃位错和螺位错的α值分别等于0.5和1.5 ^[17])，并包含了位错源长度与晶粒尺寸之间的比例因数。同时，由于在Cu-Nb合金MA过程中，粉末受到高能球的反复碰撞和挤压，局部应力集中非常严重，而应力集中对Cu-Nb合金内形成形变孪晶又起着非常重要的作用。因此，如果进一步考虑局部应力集中的影响，则式(2)变换成：

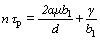                            (3)

式中：n为应力集中因子，n随球磨时间变化。

由于形变孪晶大多为Cu的形变孪晶，因此，可以忽略Nb对基体Cu层错能的影响，直接采用纯Cu参数进行计算，则γ= 7×10^-2 J/m²；μ= 48 GPa；     b=(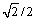)a，b₁=(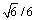)a，a为Cu的晶格参数，a=0.36 nm；α=1。

根据式(1)和(3)进行计算可得到τ_s和τ_p值随Cu基体晶粒尺寸变化的关系图(见图3)。由图3可见，随着晶粒尺寸的减小，τ_p值与τ_s值不断增加，但是τ_s值的增加速率大于τ_p值的，因此，当低于临界晶粒尺寸d_c后，τ_p值将小于τ_s值，此时在晶界处激活不全位错发射所需剪切应力低于产生全位错所需应力，形变孪晶开始形核。由此可见，当τ_p值与τ_s值相等时，材料塑性变形机制开始由滑移转变为孪生，则式(1)和(3)联立可得临界晶粒尺寸d_c：

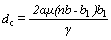                          (4)

由图2(b)~(f)可见，Cu-10%Nb合金经长时间球磨后，在尺寸约为50 nm的Cu纳米晶中开始出现形变孪晶片层，因此，该合金塑性形变开始由滑移向孪生转变的临界尺寸d_c应该为50 nm，则根据式(3)可以求得所引入的应力集中因子n=1.55。而在MA后期，随着球磨时间的延长，Cu晶粒细化与内应力的增加皆有利于形变孪生的发生，纳米孪晶数量相应增多。

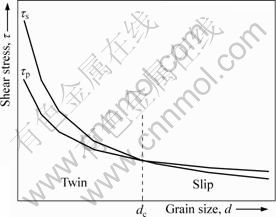
图3  晶界处位错发射所需剪切应力与晶粒尺寸之间的关系

Fig.3  Relationship between shear stress grain size at dislocation emission from GB

此外，当n=1.55时，由式(3)可得τ_p= 0.5 GPa。根据文献[18]，碰撞过程中球对粉末所施加的最大压应力可由赫兹理论^[19]给出，压力方程为

p_max=g_pν^0.4(ρ/E_eff)^0.2E_eff                                      (5)

式中：g_p为几何常数；ν为碰撞前相对速度；ρ为磨球密度；E_eff为磨球有效摩量。在本文试验条件下，g_p=0.464 6，ν=6 m/s，ρ=7.8 g/cm³，E_eff=66 GPa；根据式(5)计算可得p_max值为2.57 GPa。因此，球磨导致的最大压应力大于τ_p，这再次说明形变孪晶可能形核，并且孪晶形核与应力集中密切相关。

此外，在上述模型中，仅考虑Cu的形变孪晶，如果进一步考虑合金化了的Cu-Nb基体，由于合金化将降低基体的层错能^[20]，则根据式(3)和(4)，可以发现形变孪晶形核所需的临界尺寸d_c增加，τ_p减小。因此，可认为合金化有利于材料在室温下发生形变孪生。但并非一旦Cu晶粒或合金化Cu-Nb晶粒尺寸下降到临界尺寸以下，就会产生形变孪晶，形变孪晶的形成还与局部应力集中关系密切，因此，对于选择性孪生还需要进行更多的理论分析以及实验研究以解决这些问题。

3  结论

1) Cu-10%Nb合金在MA过程中，硬度(HV)随着球磨时间的增加而不断升高，球磨120 h后高达4.8 GPa。除固溶强化、细晶强化和应变强化外，在球磨后阶段，孪晶界强化也将有助于硬度(HV)的升高。

2) Cu-10%Nb合金在MA初期以位错胞组织为主；球磨50 h后，Cu晶粒显著细化，位错滑移逐渐困难，当Cu晶粒尺寸小于50 nm后，在局部应力集中的促进下，晶界处产生不全位错所需剪切应力低于全位错，形变孪晶可通过不全位错由晶界和晶界交叉点处的不断发射而形核，部分区域开始出现纳米形变孪晶；由于孪晶将进一步分割细化纳米晶粒，球磨120 h后，Cu平均晶粒尺寸减小至约20 nm。

3) 利用局部应力集中模型分析说明了Cu-10%Nb合金中形变孪晶的形成机制，并求得所建模型的应力集中因子n=1.55。

REFERENCES

[1] BOTCHAROVA E, FREUDENBERGER J, SCHULTZ L. Mechanical and electrical properties of mechanically alloyed nanocrystalline Cu-Nb alloys[J]. Acta Materialia, 2006, 54(12): 3333-3341.

[2] BENGHALEM A, MORRIS D G. Microstructure and mechanical properties of concentrated copper-niobium alloys prepared by mechanical alloying[J]. Materials Science and Engineering A, 1993, 161(2): 255-266.

[3] FREUDENBERGER J, BOTCHAROVA E, SCHULTZ L. Formation of the microstructure in Cu-Nb alloys [J]. Journal of materials science, 2004, 39(16/17): 5343-5345.

[4] BOTCHAROVA E, FREUDENBERGER J, SCHULTZ L. Cu-Nb alloys prepared by mechanical alloying and subsequent heat treatment[J]. Journal of Alloys and Compounds, 2004, 365(1/2): 157-163.

[5] LEI Ruo-shan, WANG Ming-pu, GUO Ming-xing, LI Zhou, DONG Qi-yi. Microstructure evolution in nanocrystalline Cu-Nb alloy during mechanical alloying[C]//YI Dan-qing. Proceedings of International Conference of Nonferrous’2007. Changsha: Transactions of Nonferrous Metals Society of China, 2007, 17(s1): s603-s607.

[6] MEYERS M A, VOHRINGER O, LUBARDA V A. The onset of twinning in metals: a constitutive description[J]. Acta Materialia, 2001, 49(19): 4025-4039.

[7] BLEWITT T H, COLTMAN R R, REDMAN J K. Low-temperature deformation of copper single crystals[J]. J Appl Phys, 1957, 28(6): 651-660.

[8] HUANG C X, WANG K, WU S D, ZHANG Z F, LI G Y, LI S X. Deformation twinning in polycrystalline copper at room temperature and low strain rate[J]. Acta Materialia, 2006, 54(3): 655-665.

[9] YAMAKOV V, WOLF D, PHILPOT S R, GLEITER H. Deformation twinning in nanocrystalline Al by molecular- dynamics simulation[J]. Acta Materialia, 2002, 50(20): 5005-5020.

[10] CHEN M W, MA E, HEMKER K J, WANG Y M, CHENG X. Deformation twinning in nanocrystalline aluminum[J]. Science, 2003, 300(23): 1275-1257.

[11] LIAO X Z, ZHAO Y H, SRINIVASAN S G, ZHU Y T. Deformation twinning in nanocrystalline copper at room temperature and low strain rate[J]. Applied Physics Letters, 2004, 84(4): 592-594.

[12] SCHIZ J, JACOBSEN K W. A maximum in the strength of nanocrystalline copper[J]. Science, 2003, 301(5): 1357-1359.

[13] ZHU Y T, LANGDON T G. Influence of grain size on deformation mechanisms: An extension to nanocrystalline materials[J]. Materials Science and Engineering A, 2005, 409(1/2): 234-242.

[14] LU Ke, LU Lei, SURESH S. Strengthening materials by engineering coherent internal boundaries at the nanoscale[J]. Science, 2009, 324(17): 349-352.

[15] WANG Yan-bo, LU Qiu-hong, SUI Man-ling. Dynamical process of twin boundary migration[J]. Journal of Chinese Electron Microscopy Society, 2007, 26(4): 302-306.

[16] VAN S H, DERLET P M, HASNOUI A. The influence of twins on the mechanical properties of Nc-Al[J]. Acta Mater, 2004, 52(8): 2251-2268.

[17] HIRTH J P, LOTHE J. Theory of dislocations[M]. New York: Wiley, 1982: 9-13.

[18] MAURICE D R, COURTNEY T H. The physics of mechanical alloying: A first report[J]. Metallurgical Transactions A, 1990, 21: 289-303.

[19] TIMOSHENKO S P, COODIER J N. Theory of elasticity[M]. New York: McGraw-Hill, 1970: 409-422.

[20] TORNTON P R, MITCHELL T E, HIRSCH P B. The dependence of cross-slip on stacking-fault energy in face-centred cubic metals and alloys[J]. Philosophical Magazine, 1962, 7(80): 13-19.

(编辑 李艳红)

基金项目：国家高技术研究发展计划资助项目(2006AA03Z517)

收稿日期：2009-11-04；修订日期：2010-03-30

通信作者：江明朴，教授；电话：0731-88830264；E-mail：wangmp@mail.csu.edu.cn