一种有效的QC-LDPC码设计及编译码仿真实现
刘丽,王中训
(烟台大学 光电信息科学技术学院,山东 烟台,264005)
摘要:为满足高的数据需求,提出一种新的QC-LDPC码。该校验矩阵的校验部分为近似下三角结构,上对角线下面的非零元素可以任意放置,因此是一种半确定的结构。这种结构的码设计灵活,性能也极高。通过对该码的不同编译码算法进行比较,提出更有效的编译码算法。MATLAB仿真表明,此结构的QC-LDPC码比双对角线结构的QC-LDPC码具有更低的误码率,快速编码算法和Offset BP-based译码算法的有效性大大提高,且可以得到近似甚至超过传统算法的可靠性。
关键词:QC-LDPC码;近似下三角结构;快速编码;Offset BP-based算法
中图分类号:TN911.22 文献标志码:A 文章编号:1672-7207(2011)S1-1068-05
Effective design of quasi-cyclic ldpc codes and its encoding and decoding simulation
LIU Li, WANG Zhong-xun
(Institute of Science and Technology for Opto-Electronics Information, Yantai University, Yantai 264005, China)
Abstract: In order to meet the demand of the data, a new QC-LDPC code was proposed. The parity part of the parity-check matrix exhibits approximate lower triangular structure and the non-zero elements can be located almost anywhere within the lower triangular area, thus, it was a half determined structure. The structure was designed to be flexible, and the performance was also extremely high. Through the comparison of different encoding and decoding algorithms about this code, more effective algorithms were proposed. The simulational results indicate that QC-LDPC code with this new structure has lower error rates compared to that with the typical dual-diagonal structure. The validity of fast encoding and Offset BP-based decoding algorithms is greatly improved and similar or higher reliability than traditional algorithm is obtained.
Key words: QC-LDPC code; approximate lower triangular structure; fast encoding; Offset BP-based decoding
通信中信道编码技术可以提高信道可靠性。低密度奇偶校验码(LDPC,Low density parity check codes)是Gallager[1]在1962年提出的一类可以用稀疏矩阵或二分图定义的线性分组码,它具有很好的接近香农极限的性能,已经成为目前和未来一代无线通讯系统及存储系统最有前景的一种码。目前LDPC的构造方法有很多,对于长码、中长码和短码有不同的构造方法,主要可以分为两大类:一是随机构造和伪随机构造,二是结构化构造方法。
QC-LDPC码(Quasi-cyclic low density parity check codes,准循环低密度奇偶校验码)是LDPC码的一个十分重要的分支,相比传统的采用随机方法构造的LDPC码,QC-LDPC码具有很多优点。首先,QC-LDPC码的编码通过使用与校验比特成正比的简单的移位寄存器就可以实现,而随机的LDPC码的编码则比较复杂,具有二次编码复杂度;其次,QC-LDPC码可以用基校验矩阵来描述,基校验矩阵中的每个元素都是z×z的方块矩阵,与校验矩阵相比,基校验矩阵较小,需要更少的存储单元;再次,通过使用合适大小的子矩阵,可以容易地把基校验矩阵扩展成不同码长的校验矩阵H[2]。
通常,QC-LDPC码的校验矩阵的校验部分构造成以近似下三角(ALT, Approximate lower tringular)的形式以实现低编码复杂度。目前,一种具有ALT结构的双对角线结构[3]的校验矩阵被广泛应用到各种通信标准中,如802.16e标准和802.11n标准。
本文作者提出QC-LDPC码的一种新的ALT结构,这种结构具有低的编码复杂度和半确定的形式,由于其设计的灵活性,这种ALT结构可以提供比双对角线结构更低的错误概率。
1 新的QC-LDPC码
定义信息比特的长度为k,校验比特的长度为m,则码字的长度n=k+m。在QC-LDPC码中,m×n的校验矩阵H由z×z个正方形子矩阵构成,其中z为扩展因子。hij为矩阵H的第(i, j)个子矩阵(i=0, 1, …, mb-1, j=0, 1, …, nb-1),mb=m/z,nb=m/z。其中,hij可以是一个0矩阵、单位矩阵I或z×z的循环矩阵P。
校验矩阵H可以分成2部分:m×k的数据部分H1和m×m的校验部分H2。因此,H可以写成下面形式:
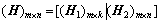 (1)
(1)
本文提出的QC-LDPC码,其m×n的校验矩阵H的校验部分H2可表示成以下形式:
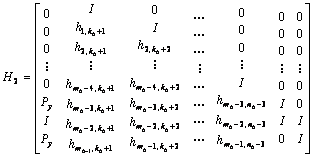 (2)
(2)
在这个结构中,校验部分的列重和双对角线结构的列重相同。也就是说,在H2中除了第一列的列重是3,(即有3个非0子矩阵)其余列子块矩阵都为2。
在第一列中,倒数第3个和最后1个子矩阵是相同的非零矩阵,都定义为循环矩阵Py,倒数第2个子矩阵定义为单位矩阵I。从第二列到倒数第三列,上对角线上的子矩阵都为I,上对角线下方的子矩阵中,每一列都有一个非零子矩阵。在最后2列中,上对角线和主对角线上的子矩阵都设为I。最后,所有剩下的子矩阵,包括上对角线以上部分的子矩阵都设为零矩阵。
总之,校验部分H2是以一种半确定方式组成的。H2中大约一半的非零子矩阵位置是一定的,而其余的非零元素允许在一个下梯形区域内任意的设置。与双对角线结构相比,这种半决定结构可提高QC-LDPC码设计的灵活性。
在LDPC码的设计中,行重是两个或三个连续的权重值。在这种ALT中,因为H2的下三角区域内所有的子矩阵可以是0,I或P,所以,H2可以有一致的或不一致的行重。因此,H1的行重也应当是一致的或不一致的,以使整个校验矩阵H的行重保持近似一致。
1.1 快速编码过程
本文采用快速编码的算法实现。长度为n的码字向量c由数据比特d和校验比特p组成。可以写成如下形式:
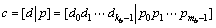 (3)
(3)
其中,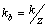 ,di和pi分别是长z的向量,
,di和pi分别是长z的向量,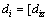
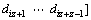 ,
,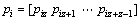 。因为
。因为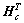 =0,可以由下式计算出矩阵H的每一行。
=0,可以由下式计算出矩阵H的每一行。
第0行:
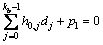 (4)
(4)
第1行:
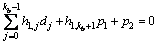 (5)
(5)
第i行:
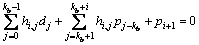 (6)
(6)
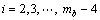
第(mb-3)行:
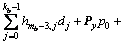
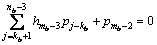 (7)
(7)
第(mb-2)行:

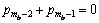 (8)
(8)
第(mb-1)行:
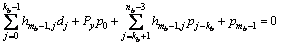 (9)
(9)
首先,通过式(4)计算得到p1,然后把p1代入式(5)中得到p2,根据p1到pi(i=2, 3, ···, mb-4)由式(6)得到
pi+i。根据最后3行,通过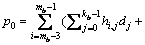
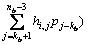 计算得到p0。最后,由p0到
计算得到p0。最后,由p0到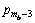 ,利用式(9)和(7),可以计算得到
,利用式(9)和(7),可以计算得到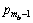 和
和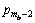 。
。
1.2 译码过程
LDPC码的译码算法的实现主要分为两类:硬判决译码和软判决译码。并且,目前提出的大多数译码算法都是通过基于置信传播(BP, Belief propagation)的迭代译码来实现。
在对数似然比(LLR, log-likehood-ratio)形式的BP译码算法中,每次约束节点的处理为:
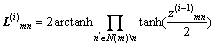 (10)
(10)
式中: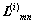 为从约束节点m传递给变量节点n的消息。
为从约束节点m传递给变量节点n的消息。
从式(10)可以看出:BP算法中涉及许多非线性的运算(如tanh(x)和arctanh(x)函数),为减小运算复杂度,陆续提出一些简化的软判决译码算法。其中Offset BP-based 算法是在BP算法的基础上简化得来的[3]。
Offset BP-based算法与BP算法有2点不同。
(1) 在Offset BP-based算法初始化时,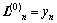 。
。
(2) 相对BP算法,Offset BP-based算法译码迭代时校验节点消息的变化为:
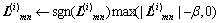 [4] (11)
[4] (11)
其中β(β>0)为偏移量因子(offset factor)。要获得最佳的译码性能,β应该随着迭代次数和SNR的变化而变化。
Offset BP-Based算法大大降低译码的复杂度,并且存在一个归一化因子β,可以进行灵活的调节,只要β选得合适就能获得接近甚至超过BP算法的性 能[5-6]。
2 仿真及分析
设定码长n=2 304,扩展系数z=96,码率R=1/2,则基校验矩阵为12行24列。构造一种无四环的QC-LDPCA码,其基校验矩阵如下所示(其中-1为0矩阵,其余每个数字代表子矩阵向右循环移位的位数):
令A码的基矩阵为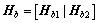 ,列出Hb1,Hb2的行重,如表1所示。
,列出Hb1,Hb2的行重,如表1所示。
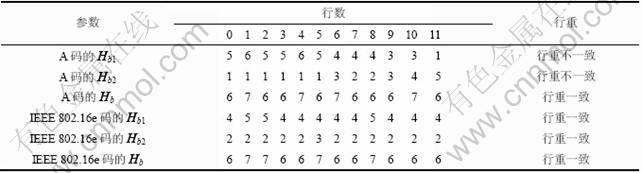
从表1可以看出:IEEE802.16e码的矩阵Hb1和Hb2以及行重Hb都几乎是一致的,它们的行重都只有两个值。对于A码,Hb1的行重为1, 3, 4, 5, 6,是不一致的;同样,Hb2的行重是1, 2, 3, 4, 5,也是不一致的。然而,Hb的行重只有2个值:行重为6的有8行;行重为7的有4行。这2个行重值也几乎一致,因此,尽管A码的行重值的顺序与IEEE 802.16e码的不相同,这2个码行重的分配是相同的。

表1 A码和IEEE 802.16e码[7]的Hb1,Hb2及Hb的行重
Table 1 Row weights of matrices Hb1, Hb2 and Hb for A and IEEE 802.16e code
在AWGN信道中仿真,采用Offset 算法(Offset BP-based)对比2个码的错误性能(误比特率(BER),Bit error rate)和误帧率(FER,Frame error rate),其中β=0.15,frame = 10,最大迭代次数为80次。
仿真结果如图1所示,A码与IEEE 802.16e码的列重相同,并且行重分配也相同,由于A码的Hb1,Hb2的行重不同,所以它比IEEE 802.16e码的性能好。
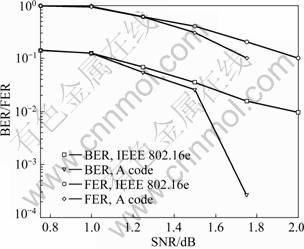
图1 A码与IEEE 802.16e码的误码率性能比较
Fig.1 Error performance comparison of A and IEEE 802.16e code
比较快速编码算法和利高斯消去的编码算法,仿真结果如图2所示。在Offset BP-based译码算法下比较,当β=0.15时,迭代10次。从图2中也可以看出:这两种编码的效果相差不多。快速编码算法用时 14.250 000 s,而高斯消去法用时207.891 000 s。由此可以看出,快速编码算法大大提高了有效性。
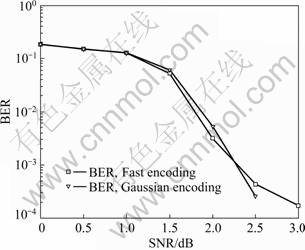
图2 快速编码算法与利用高斯编码算法的误比特率比较
Fig.2 Error performance comparison of fast and Gaussion encoding
Offset BP-based算法中β取值与译码BER的关系的仿真结果如图3所示。可见:当β=0.2时,可以达到最佳性能;并且,当β不变时,信噪比(SNR)增大,BER减小。β=0.05时Offset BP-based算法与BP算法的比较如图4所示。可以看出,两者性能很接近,并且在信噪比较大时(SNR>3),其性能超过BP算法的性能。
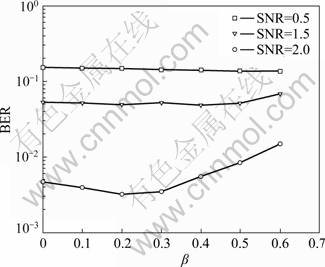
图3 β取值与BER的关系
Fig.3 Relationship between value of β and BER
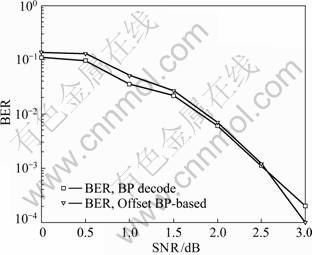
图4 QC-LDPC在Offset BP-based算法与BP算法中的比较
Fig.4 Comparison of QC-LDPC in Offset BP-based decoding and BP decoding
3 结论
(1) 提出QC-LDPC码的一种新的ALT结构,并给出有效的编码方法和译码算法实现。
(2) 在AWGN环境下,这种近似ALT结构的QC-LDPC码具有比双对角线结构的IEEE 802.16e码更好的性能,从而为无线通信领域提供了更广阔的应用前景。
(3) 采用的快速编码算法以及Offset BP-based译码算法都提高了程序运行的速度,从而提高了有效 性,并在一定程度上改善了可靠性,具有一定的应用价值。
参考文献:
[1] Gallager R G. Low-density Parity-check codes[M]. Cambridege, MA: MIT Press, 1962(8): 21-28.
[2] 尹芳, 仇洪冰, 滕舟. QC-LDPC的构造及性能仿真[J]. 桂林电子科技大学学报. 2010, 30(1): 9-12.
YIN Fang, CHOU Hong-bing, TENG Zhou. The construction of Quasi—Cyclic LDPC codes and its simulation performance[J]. Journal of Guilin University of Electronic Technology, 2010, 30(1): 9-12.
[3] Wai M T, Francis C M L. A class of QC-LDPC codes with low encoding complexity and good error performance[J]. IEEE Communication Letters, 2010, 14(2): 169-171.
[4] Marta R, Massimiliano S, Christian S. A class of quasi-cyclic LDPC codes[J]. IEEE Communication Letters, 2007, 8(3): 189-202.
[5] 刘翔, 李立华, 刘宝玲, 等. 适用LDPC码的改进译码算法[J].北京邮电大学学报, 2007, 30(5): 51-54.
LIU Xiang, LI Li-hua, LIU Bao-ling, et al. An Improved Decoding Algorithm for LDPC Codes[J]. 2007, 30(5): 51-54.
[6] 袁东风, 张海刚. LDPC码理论与应用[M]. 北京: 人民邮电出版社, 2008: 86-87.
YUAN Dong-feng, ZHANG Hai-gang. The Theory and Application of LDPC[M]. Beijing: The People's Posts and Telecommunications Press, 2008: 86-87.
[7] IEEE 802.16e/D9, Approved draft IEEE standard for local and metropolitan area networks. Part 16--2005[S].
(编辑 方京华)
收稿日期:2011-04-15;修回日期:2011-06-15
基金项目:山东省自然科学基金资助项目(ZR2009GM026)
通信作者:王中训(1965-),男,山东烟台人,博士,教授,从事信道编码、通信信号处理、水下通信的研究;E-mail:ytwzx3@tom.com