关于金属板材渐进成型的高级特征检测算法
来源期刊:中国有色金属学报(英文版)2012年第z2期
论文作者:Amar Kumar BEHERA Bert LAUWERS Joost R. DUFLOU
文章页码:315 - 322
关键词:特征检测;单点渐进成形;算法;CAPP;专家系统
Key words:feature detection; single point incremental forming; algorithm; CAPP; expert system
摘 要:提出一种关于单点渐进成形(SPIF)部件的特征检测的新型算法。基于自建的关于SPIF的CAPP专家系统,通过对几何形状、曲率、位置、方位、加工参数的综合分析,可以检测33种不同的特征可以检测。为了加快检测过程,首先使用多级边缘分割算法创建一个边缘特征的框架。随后在这个框架中,区域生长算法被用来检测剩余的特征。这个检测方法已经成功地被不同的实验所验证。采用一个双曲面半球的实验案例描述通过对检测的特征进行补偿,从而生成最优的刀具路径。结果显示,优化的刀具路径对于成形部件的精度有很大的提高。
Abstract: New advanced algorithms for the detection of detailed features in parts formed by single point incremental forming (SPIF) were developed. The features were detected in STL part specifications that took into account the geometry, curvature, location, orientation and process parameters to detect 33 different features within an expert CAPP system for SPIF. The detection process was facilitated by using multi-level edge segmentation routines that first created a frame of edge features. Within this frame, the remaining features were then detected using region growing algorithms. The results show successful detection for a number of test cases. A case study for a double curved hemisphere illustrates the generation of optimal tool paths using compensation for the detected features in the part. These tool paths lead to the improvement in the accuracy of the formed sheet metal parts.
Trans. Nonferrous Met. Soc. China 22(2012) s315-s322
Amar Kumar BEHERA, Bert LAUWERS, Joost R. DUFLOU
Department of Mechanical Engineering, Katholieke Universiteit Leuven, Celestijnenlaan 300, B-3001 Leuven, Belgium
Received 28 August 2012; accepted 25 October 2012
Abstract: New advanced algorithms for the detection of detailed features in parts formed by single point incremental forming (SPIF) were developed. The features were detected in STL part specifications that took into account the geometry, curvature, location, orientation and process parameters to detect 33 different features within an expert CAPP system for SPIF. The detection process was facilitated by using multi-level edge segmentation routines that first created a frame of edge features. Within this frame, the remaining features were then detected using region growing algorithms. The results show successful detection for a number of test cases. A case study for a double curved hemisphere illustrates the generation of optimal tool paths using compensation for the detected features in the part. These tool paths lead to the improvement in the accuracy of the formed sheet metal parts.
Key words: feature detection; single point incremental forming; algorithm; CAPP; expert system
1 Introduction
Feature analysis has served as a key tool in several manufacturing processes, including sheet metal forming. For instance, SMITH et al [1] used a relational database approach to create a feature based process plan generator for sheet metal parts. OUYANG and LIN [2] developed a feature based manufacturing cost estimator that could help a person with little knowledge of a manufacturing process to estimate the cost of a part. Likewise, GEELINK et al [3] provided a generic framework wherein a user could define feature types for sheet metal parts within a computer aided process planning system. Furthermore, conceptual design information can be easily captured by using a feature based approach, as illustrated in the work of BRUNETTI and GOLOB [4].
The detection of features is crucial to the creation of an expert system for manufacturing processes and integration of CAD and computer-aided manufacturing (CAM) [5]. An unambiguous definition of a part, available as a CAD model, facilitates the process of feature detection [6]. The file format of the CAD model determines the algorithms required to detect features. While an analytic surface model may support the ability to carry limited feature information, surface mesh formats such as STL and SLC do not have a structure for storing feature data [7,8].
To overcome this, a classification of features based on principal curvatures was illustrated by LEFEBVRE and LAUWERS [9], which was then used by VERBERT et al [10] to define a feature based accuracy improvement methodology, FSPIF, for incremental forming. In this classification, four different feature types, planes, ruled surfaces, ribs and freeform surfaces were detected. However, this broad classification is not enough to characterize the behaviour of sheet metal parts uniquely. Hence, BEHERA et al [11] proposed a hierarchical taxonomy of sheet metal features that accounts for the feature behaviour based on the location, orientation, process criteria such as failure limits and the sign of the curvature. However, this taxonomy cannot be well exploited without systematic, algorithmic implementation.
In this work, new algorithms were presented to detect the detailed features for incremental forming, which can then be used in an expert system for optimizing the process outcomes such as tool path and geometric accuracy. STL part specifications were used as input models for the feature detection.
2 Feature taxonomy
The taxonomy of features is based on the premise that all the classified features should be mutually exclusive, unambiguous and be relevant to the process output being optimized. The process output optimization criterion selected for the present taxonomy is the accuracy of parts.
2.1 Taxonomy for planar features
The planar features that are parallel to the plane of the backing plate (shown in Fig. 1) in incremental forming are classified on the basis of the orientation as horizontal features. Based on the location, these may be further classified as top, bottom and general. Non-horizontal features that are below the critical wall angle are termed ‘ordinary’, and those above the critical wall angle for failure are termed ‘above failure’. These features are abbreviated hereon using the first letters of their classification as HTP, HBP, ONHP, AFNHP, and GHP. Figure 2 shows the classification tree for planar features.
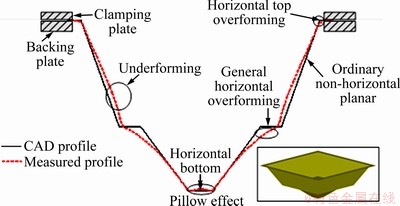
Fig. 1 Accuracy behavior of planar features
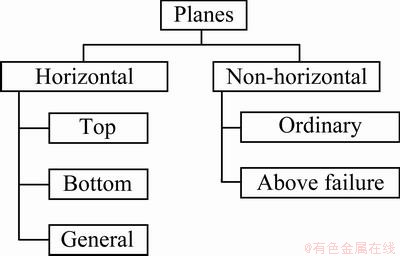
Fig. 2 Classification of planar features
2.2 Taxonomy for ruled features
Ruled surfaces can be defined by a curve called the generatrix, which moves along a line called the directrix to create the ruled surface or a surface through every point of which there is a straight line called the directrix. Hence, the orientation of the directrix can be used to classify ruled surfaces as horizontal when the directrix is in the plane of the backing plate or parallel to it, and semi-vertical when it is at an angle, as shown in Fig. 3. This classification also helps account for the differential behaviour in accuracy observed in the forming of these surfaces. Figure 4 illustrates that for a positive general horizontal ruled surface made of alumimum alloy Al-3103 of 1.5 mm in thickness, the manufactured part is underfomed until 48 mm and for the last 10 mm, it is overformed. However, the semi-vertical ruled surface is consistently underformed with no regions of overforming.
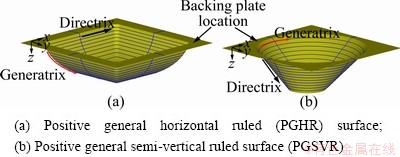
Fig. 3 Illustration of generatrix and directrix locations
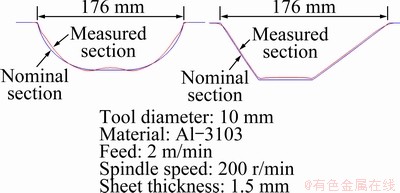
Fig. 4 Accuracy behaviour of PGHR and PGSVR features
Further, beyond a critical wall angle, a multi stage approach as described by DUFLOU et al [12] would be required for forming the part. Such features are classified as vertical ruled features. Besides, as the sign of the curvature, positive or negative, also influences the accuracy behaviour, a further classification was introduced taking this into account as shown in Fig. 5.
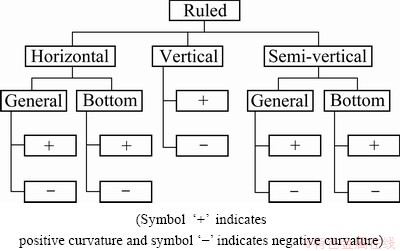
Fig. 5 Classification of ruled features
2.3 Taxonomy for freeform features
Freeform features are characterized by both principal Gaussian curvatures larger than 0, but below a threshold. Freeform features located at the bottom of the part require special processing tool paths such as bottom finishing, due to their tendency to overform or form into a pinched nipple structure as shown in Fig. 6. It is particularly interesting to observe the difference in accuracy behaviour of PGHR surface and a double curved surface as seen in Fig. 6. Although both surfaces have a similar section in YZ plane, their accuracy characteristics are remarkably different. While the double curved surface is consistently underformed the PGHR surface has zones of both underforming and overforming. The rest of the classification for freeform features is based on their curvatures, which decides the magnitude and nature of inaccuracy, as shown in the back seat orthosis part of Fig. 7. Figure 8 shows the detailed classification for freeform features.
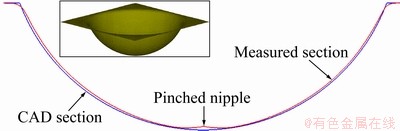
Fig. 6 Accuracy behaviour of double curved hemisphere
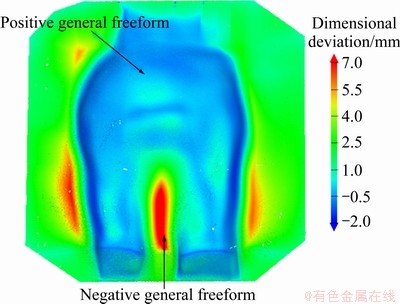
Fig. 7 Accuracy behaviour in backseat orthosis part
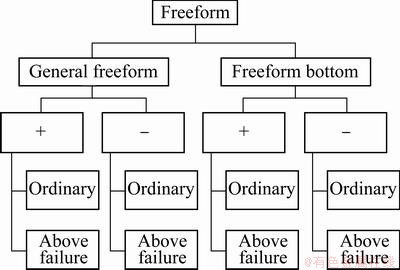
Fig. 8 Taxonomy of freeform features
2.4 Taxonomy for rib features
Ribs are features characterized by high principal curvatures greater than a given threshold. Semi-vertical rib features behave as stiff boundaries between features. Hence, they often form with higher accuracy than other features on a part, and may only require a minimal reprocessing step to be completely accurate. However, the negative horizontal ribs occurring close to the backing plate tend to be overformed. Likewise, depending on the location (general or bottom), the accuracy of the rib may vary. Hence, the taxonomy for ribs is designed similar to the taxonomy for ruled features. For the sake of unique abbreviation, ribs are indicated with the letter ‘E’. Hence, a positive general horizontal rib is indicated henceforth as PGHE.
3 Feature detection algorithms
The feature detection algorithms follow a logic that first segments a part based on the curvature. This classification identifies the ribs first based on edge based segmentation, and then uses a region growing algorithm to grow other features within the frame created by the ribs. However, the ribs themselves need to be classified according to the taxonomy. The scope of the feature detection strategy provided by VERBERT et al [10] is mostly limited to finding all the ribs in a part as a single connected feature, which limits the application of individual strategies for different types of rib features. Hence, a new algorithm is presented to detect ribs based on the detailed taxonomy.
3.1 Detection flow
The principal curvatures are calculated using the procedure outlined by LEFEBVRE and LAUWERS [9], and then sorted (Algorithm 1). The detection of ribs at different locations is done sequentially using location thresholds defined in Algorithm 2 identified automatically using the range of co-ordinates for the part calculated from the STL model vertices and a minimum curvature threshold for ribs. Algorithm 3 shows an example of the detection of the backing plate rib, and a similar logic is used for the detection of other rib features. Next, a region growing algorithm is used to detect planar, ruled and freeform features, which is based on principal curvatures. Algorithm 4 shows an example of the region growing algorithm for planar features, which is used with different curvature criteria to detect ruled and freeform features.
Algorithm 1: Sort principal curvatures
Find Principal Curvatures e1, e2 for all vertices V in the STL model of the part
Set Maximum_Principal_Curvature=Maximum(Absolute values of (e1, e2)) * Sign of principal curvature with maximum absolute value
Algorithm 2: Set depth indicators
Find Z coordinate limits of STL file, Zmin and Zmax
Size_Normalized_Threshold=|(Zmax-Zmin)|/Nominal_Section_Size
Set Top Depth Threshold=|Zmin|+Size_Normalized_ Threshold
Set Bottom Depth Threshold=|Zmax|–Size_Normalized_ Threshold
Algorithm 3: Detection of backing plate rib
for each vertex V in STL model of the part {
if ((-(Maximum_Principal_Curvature(V)) > Rib_ Curvature_Threshold) && Z_Coordinate(V) <= Top Depth Threshold)
{
Set Flag_vertex(V) = true; // Indicates V belongs to a feature
Backing_Plate_Rib_Feature_AddPoint(V);
Increment Points_In_Backing_Plate_Rib by 1
}
}
If (Points_In_Backing_Plate_Rib> Minimum_Points_ In_A_Feature) create Backing_Plate_Rib_Feature
else for all marked vertices, Set Flag_Vertex(V) = false;
Algorithm 4: Region based segmentation for planar features
for a vertex V that is not a rib or classified as belonging to a Feature Object {
Create a feature object FO with V as the seed vertex
}
Add V to the set of seed vertices
while
Remove the first vertex V1 in
for each vertex Vf in facets connected to V1 {
if ((Absolute Value of (Maximum_Principal_ Curvature(Vf)) < Max_Planar_Curvature) && (Absolute Value of (Minimum_Principal_Curvature(Vf)) < Max_Planar_Curvature) && Set Flag_vertex(Vf) = false)
{
Set Flag_vertex(Vf) = true;
FO_AddPoint(Vf);
Add Vf to the set of seed vertices
Increment Points_In_ Planar_Feature by 1
}
}
end while
If (Points_In_ Planar_Feature > Minimum_Points_ In_A_Feature) create Planar_Feature
else for all marked vertices Vp in Planar_Feature, Set Flag_Vertex(Vp) = false;
After features at the first hierarchical level of the taxonomy are identified, these features need to be further classified at the lower levels of the taxonomy to arrive at the complete identification of the feature. This requires algorithms for finding their location, orientation, curvature and process related specification.
3.2 Detection of location
The location of planar features is determined by taking an average of the ‘Z’ axis (tool axis) coordinates of the points in the feature, and checking if the average is within the thresholds defined for top, general and bottom features.
Algorithm 5: Location of planar features
if (Absolute Value of (Z Coordinate of Center of Feature) <= Horizontal_Top_Planar_Depth_Threshold) set Feature_Type = Top_Planar
if (Absolute Value of (Z Coordinate of Center of Feature)>=Horizontal_Bottom_Planar_Depth_Threshold) set Feature_Type = Bottom_Planar
if (Absolute Value of (Z Coordinate of Center of Feature) > Horizontal_Top_Planar_Depth_Threshold && Absolute Value of (Z Coordinate of Center of Feature) < Horizontal_Bottom_Planar_Depth_Threshold) set Feature_Type = General_Planar
Ruled and freeform surfaces can form continuous surfaces that extend all the way to the bottom of the part and sometimes, even being part of the bottom. Thus, it is determined that a wall angle based criterium is useful for enhanced detection.
Algorithm 6: Location of ruled and freeform features
If (Feature_AverageWallAngle <= Bottom_WallAngle_ Threshold) set Feature_Type = Bottom
else set Feature_Type = General
Ribs are well identified by using depth threshold criteria, as already discussed in Section 3.1.
3.3 Detection of orientation
The orientation of planar features is determined by using thresholds for the average angle of the normal of the points within the feature with the Z-axis.
Algorithm 7: Orientation of planar features
if(FeatureNormal.giveAngleWith(Z-Axis)< Planar_HorizontalMaxAngle) set Feature_Type= Horizontal_Planar
else set Feature_Type = Non-Horizontal_Planar
The orientation of ruled features is dependent on the angle of the directrix with the Z-axis. For horizontal ruled features, the directrix is a straight line perpendicular to the Z-axis and parallel to the backing plate. To find the orientation of the directrix, the feature is sliced at a depth located between the depth limits of the feature. This slice generates a polyline, which can be analyzed for linearity by considering points on the polyline and find X- and Y-gradients with other points on the polyline. If the number of linear sections on this polyline exceeds a threshold for linearity, then the directrix is determined to be parallel to the XY plane, and hence, the feature is classified as horizontal. To distinguish between vertical and semi-vertical features, the average wall angle of the feature is compared with a threshold for verticality, typically set by the critical wall angle of failure for the particular material and thickness.
Algorithm 8: Find number of linear sections in slice
Obtain a polyline ‘poly’ by calling slice_Feature_At (ZDepth_LinearityDetector)
if (poly != null)
{
foreach (PolyLinePoint pp in poly.polyLineList)
{
foreach (PolyLinePoint q in poly.polyLineList)
{
ygradient = Abs((q.YCoord - pp.YCoord) / (q.Point. XCoord - pp.Point.XCoord))
xgradient = Abs((q.XCoord - pp.Point. XCoord)/(q.YCoord - pp.YCoord))
if ((ygradient > InfinityGradient && xgradient < ZeroGradient) || (xgradient > InfinityGradient && ygradient < ZeroGradient)) count++;
}}}
Number of Linear Sections in Feature Slice = count
Algorithm 9: Orientation of ruled features
if (Number of Linear Sections in Feature Slice> Linearity _Threshold) set Feature_Type = Horizontal
else if (Feature_AverageWallAngle<= Vertical_Wall_ Angle_Threshold ) set Feature_Type = Semi-Vertical
else set Feature_Type = Vertical
Freeform features are not classified based on the orientation as discussed previously. Rib features use the same algorithm as ruled features, with different values for the thresholds, as a rib feature is usually smaller in dimension and thus is likely to have less linear sections. Besides, ribs fail earlier in a part with high wall angles, thereby requiring different verticality thresholds.
3.4 Curvature based classification
The classification based on curvature is relevant to ruled, freeform and rib features and is done by finding the average of the maximum principal curvatures of the points in the feature, as mentioned in Algorithm 10.
Algorithm 10: Curvature of ruled, freeform and rib features
if (Feature_Average_Maximum_Principal_Curvature>=0) set Feature_Type=Positive
else set Feature_Type=Negative
3.5 Process specific classification
The process specific classification separates out the features above failure. For planar features, this can be done easily using the wall angle of the feature, as they are defined by a single wall angle for a given material and thickness. However, for ruled, freeform features and ribs, the wall angle can vary within a feature, and hence, the maximum wall angle of the feature, and the area of the region above failure can be used to determine whether the feature will fail. Further, the failure wall angle depends on the material and thickness, which is stored in a database and used for the classification.
Algorithm 11: Failure criteria
if (Feature_Maximum_Wall_Angle>Failure_Wall_Angle_Threshold (material, thickness) && Area of Feature_Failure_Facets>Failure_Area_Threshold) set Feature_Type = Above Failure
else set Feature_Type = Ordinary
4 Results of feature detection
The successful feature detection of complex sheet metal parts depends on tuning the thresholds for the feature detection for a series of representative parts for which the expected feature types are known in advance.
4.1 Threshold specifications
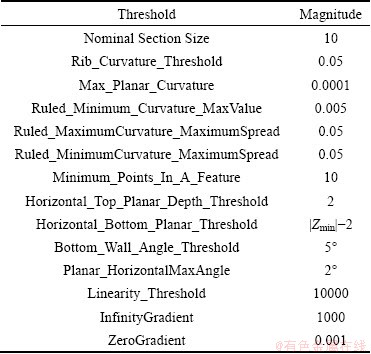
Table 1 lists the magnitudes of thresholds that are used to carry out successful feature detection on a set of 8 representative parts. Some of these thresholds may need to be adapted as a specific part definition, and also defined as functions of part size so that they are chosen automatically.
Table 1 Magnitudes of thresholds for feature detection
4.2 Case studies
The results of the edge based segmentation algorithm show clear separation of the semi-vertical ribs, as shown in Fig. 9. The remaining ribs, viz. NGHE, PGHE, and PBHE are also detected at their correct locations.
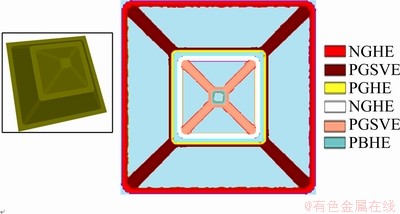
Fig. 9 Results of edge based segmentation on two-angled pyramid with horizontal plane separating pyramids
Next, the region based segmentation algorithms are tested in combination with the edge based algorithm. Figure 10 shows the results of the detection performed on horizontal ruled surfaces. The linearity detector is able to identify that the directrix is parallel to the backing plate successfully.
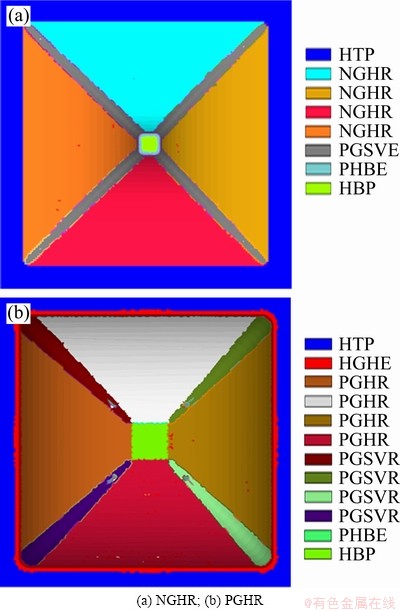
Fig. 10 Feature detection on parts with horizontal ruled surfaces
Likewise, semi-vertical ruled features are detected as shown in Fig. 11. Further, a double-curved hemisphere is detected as a positive general freeform feature illustrated in Fig. 12. Figure 12 also shows the feature detection on a composite part made of different feature types in interaction.
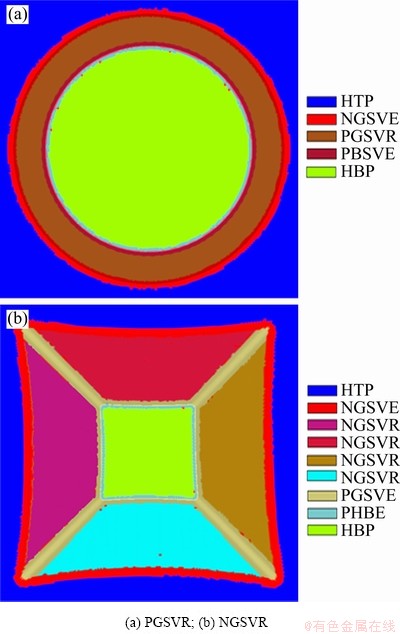
Fig. 11 Feature detection on parts with semi-vertical ruled surfaces
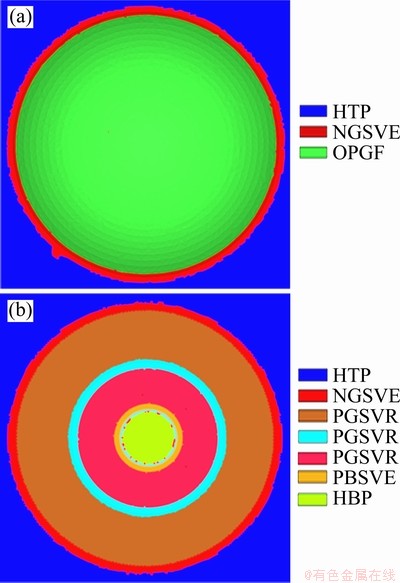
Fig. 12 Feature detection on parts with positive freeform feature (a) and combination of semi-vertical ruled features in interaction (b)
4.3 Applications for optimal tool path generation
The detected features can be joined together in a network of features, representing a conceptual graph following the procedure outlined by BEHERA et al [13]. Interactions between features can thus be accounted for and compensated by selecting intelligent tool path strategies. This is achieved by defining neighborhood algorithms, which are beyond the scope of this work. A feature based partial tool path generator is created, which uses the network and complementary tool path strategies to create optimized tool paths for individual features.
4.4 Improvements in accuracy
The detection of features based on the detailed taxonomy presented in this work enables response surface prediction of a complete set of 33 features by defining feature specific parameters for regression using multivariate adaptive regression splines, as illustrated by BEHERA et al [14]. Furthermore, the interactions between these features can now be studied more easily, and combined response surfaces predicted [15].
As part of a tool path strategy selection study, an integrated compensation strategy is devised for a double curved hemisphere. To overcome the effect of the pinched nipple, the last 2 mm of the tool path is translated to the top of the part, before beginning the tool path for the double-curved hemisphere. The overforming that is expected in the negative rib close to the backing plate is compensated by offsetting inwards the circular G03 contours close to the backing plate by using an average predicted deviation. The rest of the double curved surface is similarly offset outwards by an average predicted deviation for OPGF features. This is shown in Eq. (1):
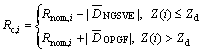 (1)
(1)
where Rc,i is the compensated radius of contour i of the tool path; Rnom,i is the nominal radius; 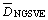 is the average predicted deviation for NGSVE feature in a double curved hemisphere;
is the average predicted deviation for NGSVE feature in a double curved hemisphere;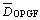 is the average predicted deviation of the OPGF feature; Z(i) is the depth at contour i and Zd is the maximum depth of the NGSVE feature, as determined by the Z-axis limits of the feature.
is the average predicted deviation of the OPGF feature; Z(i) is the depth at contour i and Zd is the maximum depth of the NGSVE feature, as determined by the Z-axis limits of the feature.
The accuracy range for the uncompensated test is [-1.32 mm, 1.79 mm] with an average deviation of 0.6 mm, while for the compensated test using the strategy discussed above, that is [-0.44 mm, 0.6 mm] with an average deviation of 0.02 mm (Fig. 13).
5 Conclusions
A detailed taxonomy of 33 features for single point incremental forming (SPIF) is presented in this work.
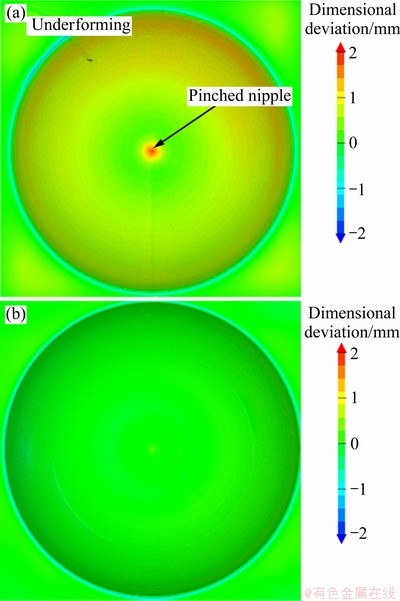
Fig. 13 Accuracy plots of double-curved hemi-sphere made using uncompensated tool path (a) and compensated tool path (b)
Algorithms are outlined that can detect these features. These algorithms are based on a multi-level edge segmentation routine followed by growing features using a region growing algorithm in the frame created by these features. The detection of features at increasing complex levels of taxonomy is essential to identify and apply unique compensation strategies that may apply to a particular feature based on its expected accuracy behaviour. The present taxonomy also takes material and thickness into account in defining critical wall angles for the parts, which in turn decide, the feature classification and use of a specific tool path strategy. Furthermore, the new feature classification routines enable mathematical compensation of features and feature interactions, with the ability to define unique parameters for each feature type and interaction. These advanced feature detection algorithms thus bring us closer to realizing a fully functional expert system for SPIF.
Acknowledgments
The authors gratefully acknowledge financial support from the FondsWetenschappelijkOnderzoek (FWO)-Vlaanderen and Chinese translation help from Yansong GUO of the Katholieke Universiteit Leuven.
References
[1] SMITH J S, COHEN P H, DAVIS J W, IRANI S A. Process plan generation for sheet metal parts using an integrated feature-based expert system approach [J]. International Journal of Production Research, 1992, 30(5): 1175-1190.
[2] OUYANG C, LIN T S. Developing an integrated framework for feature-based early manufacturing cost estimation [J]. The International Journal of Advanced Manufacturing Technology, 1997, 13(9): 618-629
[3] Geelink R, Salomons O W, van Slooten F, van Houten F J A M, Kals H J J. Unified feature definition for feature based design and feature based manufacturing [C]// Proceedings of ASME Cconference. Boston, MA, 1995: 517-533.
[4] BRUNETTI G, GOLOB B. A feature-based approach towards an integrated product model including conceptual design information [J]. Computer-Aided Design, 2000, 32(14): 877-887.
[5] HAN J H, PRATT M, REGLI W C. Manufacturing feature recognition from solid models: A status report [J]. IEEE Transactions on Robotics and Automation, 2000, 16(6): 782-796.
[6] SHAH J J. Assessment of features technology [J]. Computer-Aided Design, 1991, 23(5): 331-343
[7] KAI C C, JACOB G G K, MEI T. Interface between CAD and rapid prototyping systems. Part 1: A study of existing interfaces [J]. Int J Adv Manuf Technol, 1997, 13: 566-570.
[8] KUMAR V, DUTTA D. An assessment of data formats for layered manufacturing [J]. Advances in Engineering Software, 1997, 28(3): 151-164.
[9] LEFEBVRE P, LAUWERS B. Multi-axis machining operation evaluation for complex shaped part features [C]//Proceedings of the 4th CIRP ICME International Seminar on Intelligent Computation in Manufacturing Engineering. Sorrento, Italy, 2004: 345-350.
[10] Verbert J, Duflou J, Lauwers B. Feature based approach for increasing the accuracy of the SPIF process [J]. Key Engineering Materials, 2007, 344: 527-534.
[11] Behera A K, Vanhove H, Lauwers B, Duflou J R. Accuracy improvement in single point incremental forming through systematic study of feature interactions [J]. Key Engineering Materials, 2011, 473: 881-888.
[12] Duflou J, Verbert J, Belkassem B, Gu J, Sol H, Henrard C, Habraken A. Process window enhancement for single point incremental forming through multi-step tool paths [J]. CIRP Annals—Manufacturing Technology, 2008, 57(1): 253-256.
[13] BEHERA A K, LAUWERS B, DUFLOU J. An integrated approach to accurate part manufacture in single point incremental forming using feature based graph topology [J]. Key Engineering Materials, 2012, 504-506: 869-876.
[14] Behera A K, Verbert J, Lauwers B, Duflou J R. Tool path compensation strategies for single point incremental sheet forming using Multivariate Adaptive Regression Splines [J]. Computer-Aided Design, 2012, 45: 575-590.
[15] Behera A K, GU J, Lauwers B, Duflou J R. Influence of material properties on accuracy response surfaces in single point incremental forming [J]. Key Engineering Materials, 2012, 504-506: 919-924.
Amar Kumar BEHERA, Bert LAUWERS, Joost R. DUFLOU
Department of Mechanical Engineering, Katholieke Universiteit Leuven, Celestijnenlaan 300, B-3001 Leuven, Belgium
摘 要:提出一种关于单点渐进成形(SPIF)部件的特征检测的新型算法。基于自建的关于SPIF的CAPP专家系统,通过对几何形状、曲率、位置、方位、加工参数的综合分析,可以检测33种不同的特征可以检测。为了加快检测过程,首先使用多级边缘分割算法创建一个边缘特征的框架。随后在这个框架中,区域生长算法被用来检测剩余的特征。这个检测方法已经成功地被不同的实验所验证。采用一个双曲面半球的实验案例描述通过对检测的特征进行补偿,从而生成最优的刀具路径。结果显示,优化的刀具路径对于成形部件的精度有很大的提高。
关键词:特征检测;单点渐进成形;算法;CAPP;专家系统
(Edited by CHEN Wei-ping)
Corresponding author: Amar Kumar BEHERA; Tel: +32-489167918; E-mail: amarkumar.behera@cib.kuleuven.be
DOI: 10.1016/S1003-6326(12)61725-7

