J. Cent. South Univ. Technol. (2011) 18: 2201-2206
DOI: 10.1007/s11771-011-0963-4
Numerical simulation of asphalt mixture based on
three-dimensional heterogeneous specimen
ZHANG Xiao-ning(张肖宁)1, WAN Cheng(万成)1, WANG Dong(王栋)2, HE Ling-feng(贺玲凤)1
1. Department of Civil and Transportation Engineering, South China University of Technology,Guangzhou 510640, China;
2. Department of Civil and Environmental Engineering, Virginia Polytechnic Institute and State University,Blacksburg 24060, USA
? Central South University Press and Springer-Verlag Berlin Heidelberg 2011
Abstract: In order to verify the validity of finite element numerical simulation method for asphalt mixture, which consists of aggregates, mastic (where mastic is a kind of fine mixture composed of asphalt binder mixed with fines and fine aggregates) and air voids, based on three-dimensional (3D) heterogeneous specimen, X-ray computerized tomography (X-ray CT) was used to scan the asphalt specimens to obtain the real internal microstructures of asphalt mixture. CT images were reconstructed to build up 3D digital specimen, and the viscoelastic properties of mastic were described with Burgers model. The uniaxial creep numerical simulations of three different levels of aggregate gradation were conducted. The simulation results agree well with the experimental results. The numerical simulation of asphalt mixture incorporated with real 3D microstructure based on finite element method is a promising application to conduct research of asphalt concrete. Additionally, this method can increase the mechanistic understanding of global viscoelastic properties of asphalt mixtures by linking the real 3D microstructure.
Key words: asphalt mixture; X-ray CT; 3D heterogeneous specimen; numerical simulation
1 Introduction
Asphalt mixture is a composite material comprising aggregates, mastic and air voids. It has complicated mechanical properties [1-2]. In most cases, the asphalt mixture is assumed to be homogeneous and its microstructures are ignored. Actually, the deformation and strength of asphalt mixture are not only influenced by volume fractions of these three parts, but also affected by the spatial distribution of these three factors. Many researchers treated asphalt mixture as homogeneous material in the simulation of uniaxial creep test using finite element method. Some of them found the defects of this method, and pointed out that it was hard to simulate the real situation because the actual asphalt mixture specimens were heterogeneous. Therefore, the numerical simulation based on the real microstructure is significantly important [3-4]. Although a number of researchers used statistical mathematical method to describe the heterogeneous property of asphalt mixture such as Weibull distribution, they still cannot accurately reflect the actual internal structure of asphalt mixture [5-6].
Combined with digital image processing (DIP) and finite element method (FEM) or discrete element method (DEM), X-ray computerized tomography (CT) is used to obtain the internal structure of asphalt mixture, and the numerical simulation is performed on the basis of reconstruction digital specimen. WANG et al [7] have proposed the use of FEM-based models to characterize the mechanical properties in heterogeneous asphalt mixture. The DEM has also been employed by several researchers such as BUTTLAR and YOU [8] and CHENG [9]. Most of research about microstructure of asphalt mixture was focused on the following two aspects: 1) Quantitatively or qualitatively analyzing the internal structure of asphalt mixture [10-11]; 2) Based on one or several two-dimensional cross-sections of asphalt specimen, combined with DIP technology, two- dimensional (2D) digital specimen was established for mechanical simulation [12-15]. These studies may be more reasonable if the real three-dimensional (3D) microstructure of asphalt mixture was considered. However, limited investigations have been done on three-dimensional micromechanical modeling of asphalt mixture.
In this work, the three-dimensional (3D) finite element method (FEM) was developed to predict the deformations of three levels of aggregate gradation. Internal structures of asphalt mixture specimens utilized in this work were obtained by the X-ray CT imaging technique. From the 3D X-ray CT image, locations (coordinates) of aggregates, mastic and air voids were obtained using image analysis techniques. Then, the coordinates of aggregate, mastic, and air voids were entered into the FEM. The properties of mastic were described and transformed to FEM parameters. Finally, the predicted deformation values were compared with the laboratory measurements.
2 Experimental
2.1 Raw materials
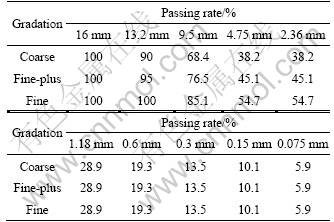
Three types of graded asphalt cements (AC), commonly utilized in Guangdong Province, China, were used. There were three levels of aggregate gradation (fine, fine-plus and coarse) with single source of aggregates, three levels of asphalt content (4.7% and 5.1% for fine and fine-plus gradations and 5.4% for coarse gradation, mass fraction), and three levels of air void content (4%, 5% and 6%). Table 1 gives the three levels of aggregate gradation. The passing rates above 2.36 mm sieve size are different but same under that for these three gradations.
Table 1 Three levels of aggregate gradation
2.2 Specimen design and preparation
Totally, nine specimens were prepared in the Asphalt Laboratory of South China University of Technology, China. The numerical simulation for large size specimen is very time-consuming, especially considering the viscoelastic properties of mastic. Therefore, the specimen size should not be too large. In this work, all specimens are cylinders with 50 mm in diameter and 50 mm in height.
2.3 Test results
All specimens were tested at 25 °C and uniaxial compression creep test was performed on these specimens. The test equipment and the deformation results are shown in Fig.1 and Fig.2, respectively. It can be seen that the fine mixture has the largest deformation, followed by fine-plus mixture and the coarse mixture. The deformation of specimens with asphalt binder is fairly small compared with specimens with aggregates. This may be due to the lack of reinforcement provided by aggregates and interlock action of aggregates which is partially enhanced by asphalt binder. The interlock action may account for a large portion of the resistance to deformation. The more the aggregates are, the more the contact is, hence the more the resistance is. It should be noted that the purpose of uniaxial compression creep test is to verify the validity of 3D FEM numerical simulation based on heterogeneous specimen.

Fig.1 Creep test equipment
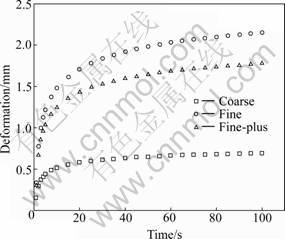
Fig.2 Deformation results
3 Digital specimen reconstructions
The digital representation of the real 3D microstructure (not a simulated 3D or 2D microstructure) of a physical specimen is named digital specimen. Computational simulation of a mechanical test, which is based on digital specimens and considers every required detail of the microstructure and its evolution, is named digital test. It is different from conventional computational simulations that assume either a continuum model or a simulated microstructure [16]. Digital specimen and test techniques permit investigation of the strength and deformation mechanisms of asphalt concrete in a microscopic way that integrates mechanism identification, numerical simulation, and experimental observations. It represents the trend for the future mix design [17].
The asphalt specimens were scanned to obtain a series of 2D images before uniaxial compression creep test, as shown in Fig.3(a). Imaging principle of CT images is different from that of optical images. CT image is a display data matrix that consists of many voxel values. The display data processed are input to image memory to show gray images which include 256 gray scales. Different gray scales represent different densities of materials. This property can be used to distinguish the three parts of asphalt mixture: aggregates, mastic and air voids. Due to computing time and the limitation of the computer memory and disk space, especially for simulation with viscoelastic material model, all the images with original 512×512 resolution were transformed into 50×50 resolution. The CT images processed were used to be 3D reconstructions. WAN et al [18] developed a reconstruction method and showed the whole procedures. A MATLAB program was developed to build up 3D finite element model. Figure 3 shows the sketch of reconstruction procedures. The final 3D model reconstructed for numerical simulation is shown in Fig.4.
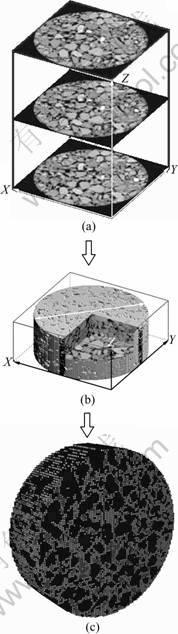
Fig.3 Reconstruction procedures of 3D digital specimen: (a) Series of continuous CT images; (b) Visualization specimen; (c) 3D digital specimen

Fig.4 3D digital specimen for uniaxial creep testing
4 Micromechanical finite element model
Mastic is a kind of typical viscoelastic material. Its properties can be described by constitutive models. The complicated constitutive models reflect the viscoelastic properties of mastic accurately, but the viscoelastic parameters are hard to be determined. On the premise of ensuring the accuracy, the constitutive model used is as simple as possible. In this work, the Burgers model was selected to describe the viscoelastic properties of mastic.
4.1 Viscoelastic model for mastic
Burgers model consists of Maxwell model and Kelvin model in parallel, as shown in Fig.5. Its constitutive equation can be expressed as [19]
 (1)
(1)
where σ is the stain, and ε is the stress,

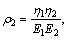

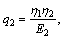
E1 and E2 are elasticity parameters, η1 and η2 are viscosity parameters.
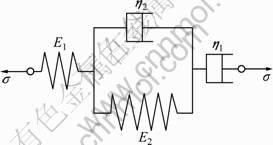
Fig.5 Burgers model
The creep equation of model under consistent stress σ0 can be written as
 (2)
(2)
where J(t) is the creep compliance function, and it can be formulated by using viscoelastic coefficients as
 (3)
(3)
The conversion relations between relaxation function and creep function can be derived according to Boltzmann superposition principle and Laplace transform. The following is the conversion equation [20]:

or
 (4)
(4)
where E(t) is the relaxation modulus; J(t) is the creep compliance.
According to conversion relations, the analytical solution of relaxation modulus for Burgers model can be calculated as
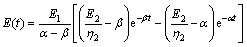 (5)
(5)
where
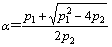
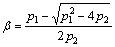
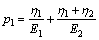

4.2 Fitting Prony parameters (Ei)
The viscoelastic properties of Burgers model should be converted to parameters accepted by finite element software. E(t) of Burgers model can be expressed with a Prony series [21]:
 (6)
(6)
where E∞ and Ei are the relaxation moduli; τi is the relaxation time.
In this work, the creep test for matrix beams was conducted using dynamic shear rheometer(DSR) to obtain Prony parameters. The raw materials used for mastic were the same as those used for AC mixtures. According to three levels of aggregates gradation listed in Table 1, the gradation of mastic could be converted, as listed in Table 2.
Table 2 Matrix gradation

The size of the mastic beam was 50 mm long, 10 mm wide and 10 mm high. The testing stage was stress controlled. The creep compliance was obtained through creep test and then converted to relaxation modulus according to Eq.(4). The Prony parameters could be fitted from relaxation modulus according to Eq.(6).
Actually, many sets of Prony parameters could be obtained from Eq.(6), but most of them did not meet the requirements. PARK and KIM [22] developed a method for selecting the relaxation time spectrum. The relaxation time spectrum chosen was τi= 10(i-4) (i=1, …, 6), and this time spectrum covered the whole length of loading time. The relaxation time spectrum and Prony parameters were obtained according to the above method, as listed in Table 3. The fitting results of relaxation modulus agreed well with the measure results, as shown in Fig.6. It was indicated that this method was effective, and then the Prony parameters were input to finite element software for the following micromechanical modeling.
Table 3 Fitting Prony parameters

5 Results and discussion
The parameters of mastic were input to ABAQUS software for three different gradations under the same temperature and loading conditions. The boundary condition imposed on the micromechanical model, and vertical displacements at the bottom face of the mixture were constrained, and the uniaxial pressure loading was applied to the top face. The INP file containing the information of loading, boundary conditions and analysis steps was imported into ABAQUS software to model uniaxial pressure test. Deformation-time profiles, as shown in Fig.7, indicate the validity of the method. It can be seen clearly that the results between simulation and test agree well, especially for fine gradation. The fine gradation also has the largest deformation, followed by fine-plus gradation and coarse gradation, which is consistent with actual experiment results. The material parameters obtained in the test of mastic are able to be used in the simulation of tests of the all specimens, which have different aggregate contents but the same material properties.
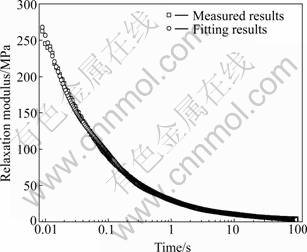
Fig.6 Fitting relaxation modulus curves of mastic

Fig.7 Simulation results compared with testing results
6 Conclusions
1) This method is different from conventional finite element simulation method based on homogeneous specimens. This simulation results agree well with experimental results. This implies that material parameters obtained from mastic test could be used in the simulation of asphalt mixture incorporated with real microstructure. In this case, the real microstructural configuration is very important in the simulative test of asphalt mixture besides the properties of mastic. This work demonstrates the power and efficacy of this modeling approach by linking the real 3D microstructure.
2) The further studies include the simulation of the 3D heterogeneous specimen using viscoelastic contact laws to develop fast computational algorithms and to reduce computational time. It is expected that the 3D models of the heterogonous specimen of asphalt mixture will assist better the understanding of load carrying mechanisms of asphalt mixtures to improve the design and construction of asphalt pavements.
References
[1] YOU Z P, ADHIKARI S, KUTAY M E. Dynamic modulus simulation of the asphalt concrete using the X-ray computed tomography images [J]. Materials and Structures, 2009, 42(5): 617-630.
[2] TAN Yi-qiu, LI Xiao-lin, ZHOU Xin-ye. Interactions of granite and asphalt based on the rheological characteristics [J]. Journal of Materials in Civil Engineering, 2010, 22(8): 820-825.
[3] BRAZ D, DA M, LAURA M G, LOPES R T. Computed tomography in the fatigue test analysis of an asphalt mixture [J]. Applied Radiation and Isotopes, 1999, 50(4): 661-671.
[4] GARBOCZI E J. Three-dimensional mathematical analysis of particle shape using X-ray tomography and spherical harmonics: Application to aggregates used in concrete [J]. Cement and Concrete Research, 2002, 32(10): 1621-1638.
[5] ZAITSEV Y B, WITTMANN F H. Simulation of crack propagation and failure of concrete [J]. Materials and Construction, 1981, 14: 357-365.
[6] YANG Sheng-feng, YANG Xin-hua, CHENG Chuan-yao. Simulation of rheological behavior of asphalt mixture with lattice model [J]. Journal of Central South University of Technology, 2008, 15: 155-157.
[7] WANG L B, FROST J D, SHASHIDHAR N. Microstructure study of west track mixes from X-ray tomography images [C]// Transportation Research Record (TRB) 80th Annual Meeting. Washington D C, 2001: 2632-2633.
[8] BUTTLAR W G, YOU Z P. Discrete element modeling of asphalt concrete: A microfabric approach [C]// Transportation Research Record (TRB) 80th Annual Meeting. Washington D C, 2001: 111- 118.
[9] CHENG Jun. Virtual fatigue tests of asphalt mixture based on discrete element method [D]. Nanjing: Southeast University, 2010: 101-120. (in Chinese)
[10] MASAD E, MUHUNTHAN B, SHASHIDHAR N, HARMAN T. Quantifying laboratory compaction effects on the internal structure of asphalt concrete [C]// Transportation Research Record (TRB) 78th Annual Meeting. Washington D C, 1999: 179-185.
[11] TASHMAN L, MASAD E, ANGELO J, BUKOWSKI J, HARMAN T. X-ray tomography to characterize air void distribution in superpave gyratory compacted samples [J]. International Journal of Pavement Engineering, 2002, 3(1): 19-28.
[12] MASAD E, SOMADEVAN N. Microstructural finite-element analysis of influence of localized strain distribution on asphalt mix properties [J]. Journal of Engineering Mechanics-ASCE, 2002, 128(10): 1105-1114.
[13] KIM H, WAGONER M P, BUTTLAR W G. Numerical fracture analysis on the specimen size dependency of asphalt concrete using a cohesive softening model [J]. Construction and Building Materials, 2009, 23(5): 2112-2120.
[14] ALVAREZ A E, MAHMOUD E, MARTIN A E, MASAD E, ESTAKHRI C. Stone-on-stone contact of permeable friction course mixtures [J]. Journal of Materials in Civil Engineering, 2010, 22(11): 1129-1138.
[15] DAI Q L. Prediction of dynamic modulus and phase angle of stone-based composites using a micromechanical finite-element approach [J]. Journal of Materials in Civil Engineering, 2010, 22(6): 618-627.
[16] COLLOP A C, SCARPAS A T, KASBERGEN C, BONDT A D. Development and finite element implementation of a stress dependent elasto-visco-plastic constitutive model with damage for asphalt [C]// Transportation Research Record (TRB) 82nd Annual Meeting. Washington D C, 2003: 179-185.
[17] ROBERT F L, MOHAMMAD L N, WANG L B. History of hot mix asphalt mixture design in the United States [J]. Journal of Materials in Civil Engineering, 2002, 14(4): 279-293.
[18] WAN Cheng, ZHANG Xiao-ning, WANG Shao-huai, WU Wen-liang. Three-dimensional digital specimen reconstruction of asphalt mixture based on X-CT technology [J]. Journal of Highway and Transportation Research and Development, 2010, 27(11): 34-36. (in Chinese)
[19] ZHANG Xiao-ning. Viscoelastic principle and application of asphalt and asphalt mixture [M]. Beijing: China Communications Press, 2006: 54-80. (in Chinese)
[20] YANG Ting-qing, LUO Wen-bo, XU Ping. Theory and application of viscoelastic [M]. Beijing: Science Press, 2004: 23-60. (in Chinese)
[21] ROBERTO F S. Finite element analysis of the mechanics of viscoelastic asphaltic pavement subjected to varying tire configurations [D]. Lincoln: University of Nebraska, 2005: 48-92.
[22] PARK S W, KIM Y R. Fitting Prony-series viscoelastic models with power-law presmoothing [J]. Journal of Materials in Civil Engineering, 2001, 13(1): 26-32.
(Edited by YANG Bing)
Foundation item: Project(51038004) supported by the National Natural Science Foundation of China
Received date: 2010-12-16; Accepted date: 2011-03-14
Corresponding author: WAN Cheng, PhD; Tel: +86-13760788619; E-mail: wanzhu198@gmail.com