Analysis on vertical steering vibration of drum shearer cutting part
来源期刊:中南大学学报(英文版)2018年第11期
论文作者:杨道龙 李建平 王雁翔 江红祥
文章页码:2722 - 2732
Key words:drum shearer; shearer cutting part; vertical steering vibration; Matlab/Simulink
Abstract: The impact of the load on the shearer is mainly transmitted through cutting part. In this paper, in order to get the vertical steering vibration characteristics of the cutting part of the drum shearer, the working condition of coal mining machine is simplified. A simplified vertical steering model and the simplified vibration model of the whole cutting part of shearer are established. The vertical steering vibration process of the cutting unit is simplified into a single freedom and one forced vibration system under harmonic excitation. The dynamic response of the cutting part under sine excitation is obtained by using Matlab/Simulink for modeling and simulation. The influence of the support rigidity and damping of the high oil cylinder on the vertical steering vibration characteristics of the cutting part is analyzed. The results show that the damping of the cylinder can reduce the vibration of the system and the stability of the swing process of cutting the part is improved.
Cite this article as: YANG Dao-long, LI Jian-ping, WANG Yan-xiang, JIANG Hong-xiang. Analysis on vertical steering vibration of drum shearer cutting part [J]. Journal of Central South University, 2018, 25(11): 2722–2732. DOI: https://doi.org/10.1007/s11771-018-3949-7.

J. Cent. South Univ. (2018) 25: 2722-2732
DOI: https://doi.org/10.1007/s11771-018-3949-7

YANG Dao-long(杨道龙)1, LI Jian-ping(李建平)2, WANG Yan-xiang(王雁翔)1,JIANG Hong-xiang(江红祥)2
1. School of Mechatronic Engineering, Jiangsu Normal University, Xuzhou 221116, China;
2. School of Engineering, China University of Mining and Technology, Xuzhou 221116, China
 Central South University Press and Springer-Verlag GmbH Germany, part of Springer Nature 2018
Central South University Press and Springer-Verlag GmbH Germany, part of Springer Nature 2018
Abstract: The impact of the load on the shearer is mainly transmitted through cutting part. In this paper, in order to get the vertical steering vibration characteristics of the cutting part of the drum shearer, the working condition of coal mining machine is simplified. A simplified vertical steering model and the simplified vibration model of the whole cutting part of shearer are established. The vertical steering vibration process of the cutting unit is simplified into a single freedom and one forced vibration system under harmonic excitation. The dynamic response of the cutting part under sine excitation is obtained by using Matlab/Simulink for modeling and simulation. The influence of the support rigidity and damping of the high oil cylinder on the vertical steering vibration characteristics of the cutting part is analyzed. The results show that the damping of the cylinder can reduce the vibration of the system and the stability of the swing process of cutting the part is improved.
Key words: drum shearer; shearer cutting part; vertical steering vibration; Matlab/Simulink
Cite this article as: YANG Dao-long, LI Jian-ping, WANG Yan-xiang, JIANG Hong-xiang. Analysis on vertical steering vibration of drum shearer cutting part [J]. Journal of Central South University, 2018, 25(11): 2722–2732. DOI: https://doi.org/10.1007/s11771-018-3949-7.
1 Introduction
Drum shearer is the core equipment of mechanized mining, which has important influence on the safety mining and production efficiency of the coal mine. Cutting part is the directly coaling assembly among all of the shearer parts. The impact of the load on the shearer is mainly transmitted through cutting part. The coal mining machine is reliable or not, and mainly depends on the operating state, dynamic performance and the characteristics of cutting coal seam in the cutting system of the shearer [1, 2]. The impact load received by the shearer in the process of cutting coal and rock is very severe, which affects the stability of the cutting operation [3, 4].
Many scholars have carried out the research on the drum type coal mining machine. WU et al [5] put forward a multi-body system dynamical model including elastic deformation effect of structure based on the rest results of principal modes of passenger car-body. Numerical simulations were carried out to analyze the influence of the car-body elastic vibration on ride comfort, which was validated with a roller test rig. EBRAHIMI et al [6] implemented an efficient and physically motivated algorithm to find the effects of multi-tooth contact as well as backlash and left and right hand side contact of the meshing teeth. Some examples compare the simulation results of rigid, partially elastic and fully elastic models. JIAO et al [7] established mechanical model of double-drum shearer based on the actual situation and working conditions, which is a basis for further dynamic analysis of the shearer. BALCI et al [8] did the cutting experiments using the pick bit with different characteristics of coal rock. The results show that the influence of axial compressive strength of coal rock on the performance of cutting mechanism is the most serious, and the performance of the cutting mechanism is greatly affected by tensile strength, static and dynamic elastic modulus of the coal rock. DU et al [9] studied the relationships between the pick arrangements of the drum with different start vanes and the cutting load fluctuation coefficient and the drum rotary speed and haulage speed were also studied. ZHAO et al [10, 11] provided sufficient references for the shearer cutting unit optimization. It is helpful to master products’ performance and propose an optimized scheme and improve design before the physical prototype manufactured. WANG et al [12] adopted the memory cutting technology to memorize the working path of the shearer. The results show that the shearer can match the change of the coal-seam boundary to achieve the self-adaptive adjustment height of the drum. GERMAY et al [13] established a continuous dynamic model of drilling system, which utilizes the specific contact boundary conditions of the drill and the rock. In this system, self-excited vibration and friction contact process are considered. Through the analysis of the model, the influence of the force and torque of the drill on the vibration of the system is obtained finally. PRATHEEPA [14] studied the dynamic characteristic parameters by using the multi-body dynamics theory. The results show that the accuracy of the parameters has a decisive influence on the simulation and calculation of the operation of the vehicle. SAHEBKAR et al [15] established a slope with axial motion and axial load of drill string system multi-body dynamic model by using the perturbation technique. The influence law of the speed, the axial compression load, the unbalance mass and the nonlinear fluid dynamics on the system is studied in detail. The natural frequencies and the corresponding mode shapes of the system are described. GUO et al [16] studied an automatically heightened technology in the shearer drum. A mathematical model of special status in coal mining machine was established and the cutting path of shearer drum was computed based on the cubic spline fitting. YANG et al [17] established simulation model of a three-bit coal auger to analyze its vibration and deflection performance with different drilling depths based on some reasonable simplifications and hypotheses of drilling tools, and designed a novel drill rod stabilizer and constructed the simulation model of a three-bit coal auger with this stabilizer compared with a normal coal auger to study vibration and deflection performance of drilling tools, which provides scientific basis for stabilizers’ arrangement form. FU et al [18] presented three types of coal ploughs and studied their structure parameters respectively using the discrete element method (DEM) to improve the coal recovery ratio and reduce energy consumption. ZHAO et al [19] proposed an EMD based simulation of the drum resistance torque method to overcome a stiff approximation of the corresponding cutting processes. DING et al [20] applied the principles of KBE to the shearer cutting unit modern design. The knowledge acquisition method of a rough set extended model based on coherence criterion about the overall technical parameter of the shearer was presented, laying a reasoning foundation for the design of cutting unit. CHENG et al [21] introduced the time-delayed displacement feedback control for a HSLDS vibration isolator with the purpose of controlling vibration and enhancing the isolation performance, and found that the time-delayed displacement feedback control not only suppresses the resonance response but also broadens the vibration isolation bandwidth compared to other active control strategies. LI et al [22] indicated that the average vibration accelerations of shearer cutting unit in the pulling direction, vertical direction, axial direction and torsional direction are 0.1518 mm/s2, 1.1428 mm/s2, 3.432×1011 mm/s2 and 0.1078 (°)/s2, respectively. WANG et al [23] built the system dynamic model of cutting unit including drum, transmission system and motor, improved the accuracy of dynamic analysis, anti-fatigue design and reliability calculation of transmission system for cutting part of shearer. GAO et al [24] studied the significant factors which affect shearer drum’s cutting performance. Orthogonal test was conducted in the coal cutting bed with model drums and model picks. YANG et al [25–27] established a model of rotation-drilling cutting according to coal cutting theory. Then, laboratory rotation-drilling cutting experiments with 28 different cutting angles δ and rotation angles ε are realized on large blocks of test coal wall using one type of conical pick to verify the interference model. The experimental results show that a small rotation angle and large cutting angle when deciding on the installation parameters of conical picks are better in the theoretical range.
Most of the scholars studied the cutting part of the coal mining machine; however, more than half of the papers focused on the multi-dynamic of the cutting part and the vibration characteristic of other products. In this paper, the vibration steering characteristics of the cutting part of the shearer is studied further. However, due to the poor environment and complicated factors of underground mine, and the limitations of experimental conditions, the vibration steering characteristic of the cutting part is only studied in theory and simulation.
2 Theory
A practical vibration system is a complex elastic system. Most of the multi-freedom vibration system can be simplified as single mathematic model. So the complex system can be analyzed according to the theory of single freedom system.
2.1 Free vibration of a damped system with a single degree of freedom
In the actual system, there is always the damping, which consumes the energy of the system. So the vibration will decay gradually and stop eventually. The typical model of single freedom vibration system includes the mass of the vibrating object, m, the stiffness of the spring, k, the damping coefficient, c, the external excitation force, F(t), and the displacement, x. The motion equation of the system is as follows, which is established by Newton’s law.
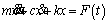 (1)
(1)
This is a two-order linear differential equation. The vibration system, which can be described by linear differential equations, is called a linear vibration system. The upper equation can be simplified to the damped free vibration equation without external force.
 (2)
(2)
Let 2a=c/m. Eq. (2) can be changed to Eq. (3).
 (3)
(3)
where 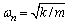 is the circular frequency of the system, rad/s.
is the circular frequency of the system, rad/s.
The characteristic root for the two-order constant coefficient differential Eq. (3) is:
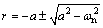 (4)
(4)
The nature of the solution depends on the characteristic root. The capacity of dimension one is introduced.
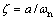 (5)
(5)
where ζ is the damping ratio. According to the relation between the damping ratio and 1, the value of the characteristic value is determined. When ζ=1, the characteristic root is a double root and the solution is:
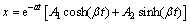 (6)
(6)
where 
It can be seen that the movement of the system is not a vibration according to Eq. (6), and with the increase of time, the movement disappeared; when ζ is the critical damping and ζ=1; the characteristic root of the solution is the double root, and the solution of the equation is:
 (7)
(7)
Through this equation, it can be seen that the motion of the system is no longer a vibration, but with the increase of the time, the movement will disappear; when ζ<1, the characteristic root of the solution is conjugate complex roots.
Let
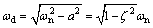 (8)
(8)
The initial displacement of a vibrating object is x0. At the beginning of the initial velocity is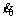 and the response of the system under the initial condition is shown in Eq. (9).
and the response of the system under the initial condition is shown in Eq. (9).
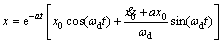 (9)
(9)
The equation can also be written as follow.
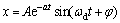 (10)
(10)
Through Eq. (10), the vibration of the system is periodic with small damping. The natural frequency for damped vibration is ωd; the natural frequency of the damped vibration is less than no damping in the case. The amplitude Ae–at decays exponentially with time. Therefore, the influence of damping on free vibration is as follows:
1) The vibration period.
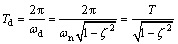
Because ζ<1, Td 2) The vibration amplitude decays. The ratio of two adjacent amplitudes is indicated by η: In Eq. (11), damping coefficient is η. The greater the damping, the faster the vibration decays. 2.2 Forced vibration of single degree of freedom system Forced vibration is generated when the system under the condition of continuous external excitation. The energy of the system to be damped is compensated by the external excitation of the system so that the system can vibrate all the time. Forced vibration can be divided into harmonic, periodic and arbitrary excitation according to the difference of the exciting force. The vertical steering of the shearer cutting is simplified as a single degree of freedom vibration system and the incentive is harmonic force. This paper focuses on the forced vibration which is caused by harmonic excitation. Under a harmonic excitation force of F=F0sin(ωt), the differential equation of motion for the system is: where Equation (12) is the second order constant coefficient of non homogeneous linear differential equation. The full solution of the equation is composed of two parts. They are the corresponding general solution x1 of homogeneous equation and non-homogeneous differential equation solution x2, respectively. The general solution of the homogeneous equation is transient response. The response will decay to zero slowly with the increase of time. The x2 is the special solution of non-homogeneous equation. The form is a constant amplitude vibration. where B is the amplitude of forced vibration, The generate solution of the equation is shown in Eq. (15). The initial conditions are x(0)=x0 and The response of forced vibration of single freedom system under harmonic excitation force is represented in Eq. (16). Thus, the whole response process of the cutting part of shearer cutting unit is composed of three parts. The first part is purely forced vibration response. It is a steady-state harmonic vibration response, which has the same frequency with the harmonic excitation force. The phase delays φ than the excited force. The second part is a damped free vibration response, which is related to the initial conditions and is independent of the excitation force. The response does not exist in the zero initial condition. The third part is the free vibration response. The amplitude of the response is related to the vibration force. The vibration frequency is the same as the damped free vibration. The last two parts are called transient vibration, which is transient response. The transient response is generated only at the beginning of the vibration, Due to the existence of the damping in system, the response of the system decays to zero very fast with the increase of time. Then the system will keep stable forced vibration under the action of exciting force. From the beginning of the vibration to the steady state of the forced vibration, a time course transition is required, and the length of the process is related to the size of the damping. 3 Mechanics model 3.1 Structure of cutting part of shearer The installation layout and structure of the cutting part of the drum type shearer are shown in Figure 1, which includes the roller, the rocker arm, the hydraulic cylinder and the fuselage four parts mainly. In the installation process of the cutting part, the hydraulic cylinder is installed in the lower part of the fuselage bottom bracket, and the cutting part and the traction part are connected by the high strength hydraulic bolt. In order to improve the adaptability of different coal seams, the cutting part mainly uses the hydraulic cylinder as the power device to drive the rocker arm up and down. The structure of the cutting part is so complex that it is necessary to be simplified before the analysis. Figure 1 Installation layout and structure simplified of cutting unit (1–Coal mining machine body; 2–Hydraulic cylinder; 3–Rocker arm; 4–Screw drum) In the process of the steering, the dynamic load of the working mechanism of the shearer is transferred to the hydraulic cylinder by the arm. Cylinder will produce a strong impact load. The impact action will have an effect on the high swing of the shearer cutting part. At the same time, the oil cylinder also plays a supporting role. This paper mainly analyzes the influence of the dynamic parameters of the cylinder on the swing of the cutting part. 3.2 Vibration model In the process of cutting coal and rock in the cutting part of shearer, the load of the spiral roller is changed randomly because of the inhomogeneity of coal bed and the change of position and quantity of the bits in the cutting section. The process can be simplified into the analysis of the alternating load in three directions [28] as follows: where Fa, Fb and Fc are the components of spiral drum loads in line, horizontal and axial directions, N; Ra, Rb and Rc are the maximum amplitudes of the three directions, N; ωa, ωb and ωc are the change frequencies of the three directions, rad/s. In the research of the high swing of the cutting part, the vibration of the roller in the high plane is mainly considered. So the load of the drum is simplified into Fa and Fb in the vertical plane. At the same time, the unbalanced centrifugal force generated by the eccentric mass of the roller during the process of the rotation is also affected by the height of the cutting part. For ease of analysis, the drum is considered a particle and the rotation is not considered. The quality of the roller is considered only on the effects of high swing characteristics. The force produced by the drum is directly affecting the end of the arm. The influence of the drum eccentricity on the vibration of the rocker can be replaced by the periodic variation of the force. According to the load characteristics of the coal mining machine, the average load is added to the sinusoidal load, which makes the application of the load more in line with the loading conditions of the working mechanism of the shearer. In the establishment of the vertical steering vibration model of the cutting part of shearer, the vertical steering hydraulic cylinder is equivalent to hydraulic spring damping vibration system. The vertical steering vibration model of the cutting part is shown in Figure 2. According to the model shown in Figure 2 and the principle of moment balance, the vertical steering vibration equation of the cutting part is: where J is the moment of inertia of the spiral drum and the rocker arm at the point O, kg·m2; Figure 2 Vertical steering vibration model of cutting part The analysis shows that the torques at the point O of the whole body include the exciting moment, the torque generated by the gravity and the torque of the cutting force. According to Figure 2, the exciting torque is: where Rx and Ry are the applied load, kN; L1 is the length of the big rocker arm, m. Rx and Ry are shown in Eq. (20). where Rp is the maximum amplitude of the eccentric force generated by the machining and assembly of the screw drum and the bits arrangement, N; R0 is The average load in horizontal direction, N; R1 is the average load in plumb direction, N; ω is the angular velocity of the screw drum, N. According to Figure 2, the torque generated by the weight is as follows: where m1 is the concentrated quality of spiral roller, kg; m2 is the concentrated quality of rocker arm, kg. Putting Eqs. (19), (20) and (21) into Eq. (18), the result is as follows: where Mc is the cutting resistance torque, N·m. Since the vibration swing angle of the rocker arm at point O is small, the equation of sinθ=θ can be got approximately. The displacement of the hydraulic cylinder is: The vibration speed of the hydraulic cylinder is: As a result, the moment of inertia of the screw drum and the rocker arm at point O is as follows: Putting Eqs. (23), (24) and (25) into the Eq. (22), the result is as follows: The frequency of the external load is related to the rotation frequency of the spiral screw drum. According to the relevant information, general analysis can make ωa=ωb=ω. Equation (26) is finished and the result is as follows: Equation (27) is the two-order differential equation, which is the typical single freedom vibration equation. The equation provides a theoretical basis for the subsequent dynamic simulation. 4 Simulation In front of the paper, the assumption and simplification of the cutting part of the drum shearer has been done and the single freedom vibration model of the cutting part has been established. In order to study the vibration characteristics of the cutting part of shearer in the process of vertical steering. The support rigidity and damping of the hydraulic cylinder have effect on the vertical steering characteristic of the cutting part. Dynamic simulation of the vertical steering process of the cutting is got by Matlab/ Simulink. 4.1 Simulation model The vertical steering vibration mathematical model of the cutting part is established. The values of the related parameters are shown in Table 1. Table 1 Relevant parameter setting of cutting part of shearer Because the parameters of kh and ch are the main dynamic parameters of the cylinder, it is necessary to select different values of the parameters to take the simulation. The simulation based on the differential equation mathematic model is to establish the differential equation model in essence. Therefore, the integral module can be used to complete the simulation by using the method of step by step integral. angular velocity According to the idea showed above, the Simulink simulation model is shown in Figure 3. The name of the model is jgxt2.mdl. The modules shown in Figure 3 can be found in the source module group, continuous set of module group, the mathematical module group and the sink module group respectively, which are all in the Simulink module library. 4.2 Result analysis The power parameters of the vertical steering cylinder need to be determined before simulation. According to the analysis of the vertical steering system in Ref. [15], the hydraulic spring stiffness is related to the position of the piston rod in the hydraulic cylinder. When the piston rod is in the middle position, the hydraulic spring rigidity is the minimum. When the piston rod is in the two ends of the hydraulic cylinder, the hydraulic spring stiffness is the largest. Therefore, the hydraulic spring should be understood as a dynamic spring rather than the steady state spring. The stiffness of the hydraulic cylinder is calculated to be 3.5×106 N·s/m. Through the analysis of dynamic characteristics of the vertical steering mechanism of coal mining machine, the damping of hydraulic cylinder, the hydraulic oil viscosity, the piston radius, the piston thickness and the piston are related to the gap between the gaps and the inner walls of the cylinder. The vibration form of the hydraulic cylinder oil pressure, cutting department, the body and the components fixed on body are all less damping shock. The critical damping of the hydraulic cylinder is obtained by calculation as 8.5×106 N·s/m. Figure 3 Simulation model of Simulink In order to analyze the law that the support stiffness and damping of the hydraulic cylinder influence on the vertical steering vibration of the cutting part, the combination groups of different damping and stiffness are divided into four groups, as shown in Table 2. Table 2 System damping rigidity setting The four groups of parameters were substituted into the function expression and calculated in the simulation model respectively. The angular acceleration It can be seen that the vibration of the cutting system is a transient response under the action of sinusoidal excitation force in Figure 4. The steady state response of the system is a constant amplitude vibration after a period of time. The angular acceleration and acceleration of the whole system are fluctuating with the zero value, and the amplitude of the fluctuation is different under different initial conditions. When the system reaches the steady state, the vibration period is 2.05 s. The frequency of the vibration is the same as the excitation force, which is the line with the theory of the second section. In the four cases, the difference of the system response is mainly in the process of transient vibration. Figure 4 Four groups 1 (a), 2 (b), 3 (c) and 4 (d) of response curves: When the stiffness of the high hydraulic cylinder is the same and the damping is different, the amplitude of the transient oscillation of various curves in Group 1 is smaller than that in Group 2. The reason is that the damping in Group 1 is greater than that in Group 2. A lot of energy is consumed by the vibration system, and the energy consumption in the damped vibration can cause the decrease of the amplitude. The transient response time of each curve in Group 2 is 1.7 s, and in Group 1 it is 2.3 s. The transition time of the curve in Group 1 is shorter, and it will get into the steady state more quickly. The reason is that the vibration system has less energy and the vibration attenuation is more slow. So the response time is longer. It can be concluded that increasing the damping of the hydraulic cylinder can reduce the transient vibration of the cutting mechanism, and make the system quickly get into the steady state and realize the smooth operation. When the damping of the vertical cylinder is same and the stiffness is different, the amplitude of the transient oscillation of various curves in Group 3 is bigger than that in Group 4. The transition time of the curves in Group 4 is the same as that in Group 3 and both are 1.7 s. Because the damping of the vibration system has not changed, the energy consumption of the system is same. The damping vibration response time is basically same. The vibration frequency of each curve in Group 4 is significantly higher than that in Group 3. The reason is that the change of the stiffness affects the transient vibration frequency, that is, the shock attenuation of the system is more intense with smaller rigidity. It can be concluded that the increase of the rigidity of the hydraulic cylinder can reduce the vibration of the cutting mechanism, and make the system get into the steady vibration state smoothly. 5 Conclusions The vertical steering vibration process of the cutting part is simplified into the single freedom vibration under harmonic excitation force. The corresponding vibration equation is obtained by deriving the relevant theory, and the whole response of the system is composed of three parts, namely pure forced vibration response, damped free vibration response and free vibration response respectively. The transient response of the system is generated at the beginning of the vibration, and the vibration force is kept stable under the action of the exciting force. The time from the beginning of the vibration to the steady state of the forced vibration is related to the ramping of the system. Through the reasonable assumption and simplification of the coal mining machine, a simplified mechanical model of the cutting part of shearer is established. The hydraulic cylinder of the shearer is simplified to a damped hydraulic spring damping system. The cutting part of shearer is regarded as a rigid body around a fixed point. The vertical steering vibration model of the cutting part is established. The vertical steering dynamic simulation model of the cutting part of shearer is established by using the integral module in Matlab/Simulink. The response curve of angular acceleration, angular velocity and angular displacement of the rocker arm are obtained by simulation with different rigidity and damping of the hydraulic cylinder. The results show that increase of the damping and stiffness of the hydraulic cylinder can reduce the vibration of the system and improve the stability of the process. References [1] DOLIPSKI M, JASZCZUK M, CHELUSZKA P. Designing of new energy-saving cutting drums of longwall shearers [J]. Australasian Institute of Mining and Metallurgy Publication Series, 2015, 1: 331–340. [2] LI Li, NI Song-song. Shearer gearbox fault diagnosis based on improved wavelet denoising pretreatment and EEMD [J]. Journal of Central South University (Science and Technology), 2016, 47(10): 3394–3400. DOI: 10.11817/j.issn. 1672-7207.2016.10.016. (in Chinese) [3] LUO Chen-xu, JIANG Hong-xiang, CUI Xin-xia. Experimental study on the axial force of shearer drum cutting coal and rock [J]. Recent Patents on Mechanical Engineering, 2015, 8(1): 70–78. DOI: 10.2174/ 2212797608666150309235530. [4] WANG Qi-guang, XIE Xi-chun, CHEN Fei, HAN Zhen-duo, CHEN Chong. Simulative cutting test of the working unit of shearer for surface mines [J]. Journal of China University of Mining and Technology, 1996, 25(4): 12–16. (in Chinese) [5] WU P, ZENG J, DAI H. Dynamic response analysis of railway passenger car with flexible carbody model based on the semi-active suspensions [J]. Vehicle System Dynamics, 2004, 41: 774–783. [6] EBRAHIMI S, EBERHARD P. Rigid-elastic modeling of gear wheels in multibody systems [J]. Multibody System Dynamics, 2006, 16(1): 55–71. DOI: 10.1007/s11044- 006-9021-7. [7] JIAO Li, LI Xiao-huo, YAO Ji-quan. Dynamics analysis of double-drum shearer and mechanical model establishment [J]. Journal of Liaoning Technical University, 2007, 26(4): 602–603. DOI: 1008-0562(2007)04-0602-02. (in Chinese) [8] BALCI C, BILGIN N. Correlative study of linear small and full-scale rock cutting tests to select mechanized excavation machines [J]. International Journal of Rock Mechanics & Mining Sciences, 2007, 44(3): 468–476. DOI: 10.1016/ j.ijrmms.2006.09.001. [9] DU Chang-long, LIU Song-yong, CUI Xin-xia. Study on pick arrangement of shearer drum based on load fluctuation [J]. Journal of China University of Mining and Technology, 2008, 18(2): 305–310. DOI: 10.1016/S1006-1266(08)60065- 6. [10] ZHAO Li-juan, MA Yong-zhi. Reliability research on shearer cutting unit based on multi-body dynamics [J]. Journal of the China Coal Society, 2009, 34(9): 1271–1275. DOI: 10.13225/j.cnki.jccs.2009.09.015. (in Chinese) [11] ZHAO Li-juan, WANG Cheng-yun. Modeling and dynamic simulation of shearer cutting unit [J]. Journal of Engineering Design, 2010, 17(2): 119–23. (in Chinese) [12] WANG Zhong-bin, XU Zhi-peng, DONG Xiao-jun. Self-adaptive adjustment height of the drum in the shearer based on artificial immune and memory cutting [J]. Journal of the China Coal Society, 2009, 34(10): 1405–1409. DOI: 10.13225/j.cnki.jccs.2009.10.012. (in Chinese) [13] GERMAY C, DENO [14] PRATHEEPA B. Modeling and simulation of automobile suspension system [J]. Frontiers in Automobile and Mechanical Engineering, 2010, 43(2): 377–382. DOI: 10.1109/FAME.2010.5714866. [15] SAHEBKAR S, GHAZAVI M, KHADEM S, GHAYESH M. Nonlinear vibration analysis of an axially moving drillstring system with time dependent axial load axial velocity in inclined well [J]. Mechanism and Machine Theory, 2011, 46(5): 743–760. DOI: 10.1016/j.mechmachtheory.2010.12. 003. [16] GUO Wei, ZHU Ning, ZHAO Shuan-feng. A method of calculation for the shearer drum cutting path [M]// Informatics in Control, Automation and Robotics. Berlin Heidelberg: Springer, 2011: 389–396. DOI: 10.1007/978-3- 642-25899-2_52. [17] YANG Dao-long, LI Jian-ping, WANG Yan-xiang, JIANG Hong-xiang. Research on vibration and deflection for drilling tools of coal auger [J]. Journal of Vibro Engineering, 2017, 19(7): 4882–4897. DOI: https://doi.org/10.21595/jve.2017. 18581 [18] FU Lin, DU Chang-long, LI Jian-ping, YANG Dao-long. Structure and parameter analysis of auger miner’s coal plough [J]. Journal of Central South University (Science and Technology), 2017, 48(3): 675–683. DOI: 10.11817/ j.issn.1672-7207.2017.03.016. (in Chinese) [19] ZHAO Shuan-feng, GUO Wei. An EMD based simulation of the drum resistance torque spectrum of a shearer [C]// IEEE International Conference on Computer Science and Automation Engineering. IEEE, 2012, 3: 367–371. DOI: 10.1109/CSAE.2012.6272974. [20] DING Hua, YANG Zhao-jian. Method and system of shearer cutting unit modern design oriented to KBE [J]. Journal of the China Coal Society, 2012, 37(10): 765–1770. DOI: 10.13225/j.cnki.jccs.2012.10.028. (in Chinese) [21] CHENG Chun, LI Shun-ming, WANG Yong, JIANG Xing-xing. Performance analysis of high-static-low-dynamic stiffness vibration isolator with time-delayed displacement feedback [J]. Journal of Central South University, 2017, 24(10): 2294–2305. DOI: https://doi.org/10.1007/s11771- 017-3641-3. [22] LI Jian-ping, GUO Hui-zhen. Vibration characteristics of shearer cutting unit based on multi-body dynamics [J]. Electronic Journal of Geotechnical Engineering, 2014, 19(4): 3195–3208. [23] WANG Yong, SUN Dong-ye, LIU Chang-zhao. Study on characteristics of external load of transmission system for cutting unit of shearer under multiple load cases [J]. Computer Modelling and New Technologies, 2014, 18(12): 326–330. [24] GAO Kui-dong, DU Chang-long, LIU Song-yong, FU Lin. Analysis on significance of the factors influencing on shearer drum cutting performance [J]. International Journal of Oil, Gas and Coal Technology, 2014, 7(4): 386–98. DOI: 10.1504/IJOGCT.2014.062170. [25] YANG Dao-long, LI Jian-ping, WANG Li-ping, GAO Kui-dong, TANG You-hong, WANG Yan-xiang. Experimental and theoretical design for decreasing wear in conical picks in rotation-drilling cutting process [J]. International Journal of Advanced Manufacturing Technology, 2015, 77(9): 1571–1579. DOI: 10.1007/ s00170-014-6472-5. [26] YANG Dao-long, LI Jian-ping, DU Chang-long, LIU Song-yong, ZHENG Ke-hong, JIANG Hong-xiang. Wear performance of conical pick in rotary-drilling cutting process [J]. Electronic Journal of Geotechnical Engineering, 2015, 20(8): 2031–2040. [27] YANG Dao-long, LI Jian-ping, ZHENG Ke-hong, JIANG Hong-xiang, XU Han-dong, LIU Song-yong. High-hardness alloy substituted by low hardness during drilling and cutting experiments of conical pick [J]. International Journal of Rock Mechanics and Mining Sciences, 2017, 95: 73–78. DOI: 10.1016/j.ijrmms.2017.04.006. [28] DENG Jian-yuan, LV Gang-ming, LI Guo-bing, ZHANG Guo-mei. Vertical sectorization using beam steering in cellular communication systems [C]// IEEE/CIC International Conference on Communications in China- Workshops. IEEE, 2014: 21–25. DOI: 10.1109/ICCChinaW. 2014.7107860. (Edited by YANG Hua) 中文导读 采煤机截割部垂直方向振动分析 摘要:采煤机负载对采煤机的振动冲击主要通过截割部进行传递。为得到滚筒式采煤机截割部的垂直振动特性,对采煤机工况进行合理简化,建立了采煤机截割部垂直简化模型,进而建立了采煤机截割部整体机构的振动数学模型。将采煤机截割部垂直振动过程简化为在简谐激振力作用下的单自由受迫振动系统,运用Matlab/Simulink进行建模仿真,得到截割部在正弦激振下的垂直摆动动态响应,分析了调高油缸的支撑刚度与阻尼对截割部垂直振动特性的影响。结果表明,增大调高油缸的阻尼可以减轻系统的振动,提高截割部调高过程的稳定性。 关键词:采煤机;截割部;垂直方向振动;Matlab/Simulink Foundation item: Project(BK20160250) supported by the Natural Science Foundation of Jiangsu Province, China; Project(17XLR028) supported by the Natural Science Foundation of Jiangsu Normal University, China Received date: 2017-09-22; Accepted date: 2018-01-21 Corresponding author: YANG Dao-long, PhD, Lecturer; Tel: +86-15952152812; E-mail: ydl_726@163.com; ORCID: 0000-0003- 0237-9969 (11)
(11) (12)
(12)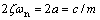 ,
,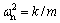 and
and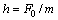 .
.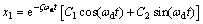 (13)
(13)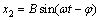 (14)
(14) φ is the phase difference between forced vibration response and exciting force,
φ is the phase difference between forced vibration response and exciting force, 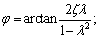 δst is the static deformation,
δst is the static deformation, 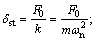 λ is the ratio of frequency between excitation and natural,
λ is the ratio of frequency between excitation and natural,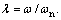

 (15)
(15) The integral constants C1 and C2 can be got by substituting in the equation and its derivative expression. So we can get the whole solution:
The integral constants C1 and C2 can be got by substituting in the equation and its derivative expression. So we can get the whole solution: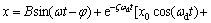
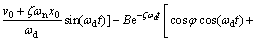
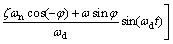 (16)
(16)
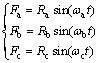 (17)
(17)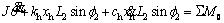 (18)
(18)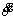 is the angular acceleration of the rocker arm at the point O, rad/s2; kh is the hydraulic spring rigidity of hydraulic cylinder, N/m; xh is the displacement of hydraulic cylinder, m;
is the angular acceleration of the rocker arm at the point O, rad/s2; kh is the hydraulic spring rigidity of hydraulic cylinder, N/m; xh is the displacement of hydraulic cylinder, m; 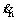 is the movement speed of hydraulic cylinder; φ1 is the angle between the big rocker and the horizontal plane, (°); φ2 is the angle between the small rocker arm and the piston rod of the hydraulic cylinder, (°); L2 is the length of the small rocker arm, m; ∑Mo is the whole external moment at the point O.
is the movement speed of hydraulic cylinder; φ1 is the angle between the big rocker and the horizontal plane, (°); φ2 is the angle between the small rocker arm and the piston rod of the hydraulic cylinder, (°); L2 is the length of the small rocker arm, m; ∑Mo is the whole external moment at the point O.
 (19)
(19)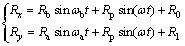 (20)
(20)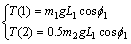 (21)
(21)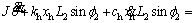
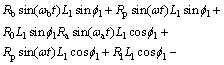
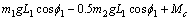 (22)
(22)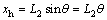 (23)
(23)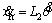 (24)
(24)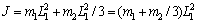 (25)
(25)
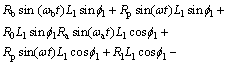
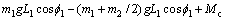 (26)
(26)

 (27)
(27)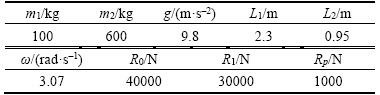
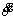 is the angular acceleration of the rocker arm; the function result of the integral module is the
is the angular acceleration of the rocker arm; the function result of the integral module is the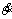 ; the angular displacement θ is obtained by the integral module. The angular acceleration
; the angular displacement θ is obtained by the integral module. The angular acceleration 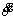 is got after the operation between
is got after the operation between 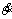 and θ. So the cycle continues. The response curve of the angular acceleration
and θ. So the cycle continues. The response curve of the angular acceleration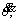 angular velocity
angular velocity 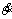 and angular displacement θ will be obtained.
and angular displacement θ will be obtained.

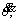 angular velocity
angular velocity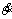 and angular displacement θ, response curves of the swing arm of the shearer are measured. The four groups of the response curves are shown in Figure 4, which are obtained by simulation.
and angular displacement θ, response curves of the swing arm of the shearer are measured. The four groups of the response curves are shown in Figure 4, which are obtained by simulation.
 L V, DETOURNAY E. Multiple mode analysis of the self-excited vibrations of rotary drilling systems [J]. Journal of Sound and Vibration, 2009, 325(1): 362–381. DOI: 10.1016/j.jsv.2009.03.017.
L V, DETOURNAY E. Multiple mode analysis of the self-excited vibrations of rotary drilling systems [J]. Journal of Sound and Vibration, 2009, 325(1): 362–381. DOI: 10.1016/j.jsv.2009.03.017.

