J. Cent. South Univ. (2017) 24: 665-674
DOI: 10.1007/s11771-017-3467-z

Modeling and monitoring of nonlinear multi-mode processes based on similarity measure-KPCA
WANG Xiao-gang(王小刚), HUANG Li-wei(黄立伟), ZHANG Ying-wei(张颖伟)
College of Information Science and Engineering, Northeastern University, Shenyang 110819, China
 Central South University Press and Springer-Verlag Berlin Heidelberg 2017
Central South University Press and Springer-Verlag Berlin Heidelberg 2017
Abstract: A new modeling and monitoring approach for multi-mode processes is proposed. The method of similarity measure(SM) and kernel principal component analysis (KPCA) are integrated to construct SM-KPCA monitoring scheme, where SM method serves as the separation of common subspace and specific subspace. Compared with the traditional methods, the main contributions of this work are: 1) SM consisted of two measures of distance and angle to accommodate process characters. The different monitoring effect involves putting on the different weight, which would simplify the monitoring model structure and enhance its reliability and robustness. 2) The proposed method can be used to find faults by the common space and judge which mode the fault belongs to by the specific subspace. Results of algorithm analysis and fault detection experiments indicate the validity and practicability of the presented method.
Key words: process monitoring; kernel principal component analysis (KPCA); similarity measure; subspace separation
1 Introduction
As a crucial component in modern process industries, process monitoring has been concentrated on for more than twenty years, and various methods have been developed for fault detection and diagnosis. Process industries play a key role as a pillar of the national economy, such as chemical industry, electric power, metallurgy; it may lead to huge economic losses and even injury if the process ignores the failures. Therefore, besides the necessity to implement a good control strategy for industrial process, it is also important to study process monitoring and fault diagnosis methods [1-4].
One of the popular multivariate statistical methods employed for fault detection is principal component analysis (PCA) [5, 6]. However, PCA assumes linear correlation among the variables, which degrades the performance of conventional PCA in monitoring the nonlinear systems. Scholars have proposed KPCA based on kernel, which can solve such problems effectively [7-10]. For multi-mode characteristics of complex processes, some scholars have proposed improved multi-mode process modeling methods based on the traditional PCA/PLS, such as HWANG [11], and LANE [12]. They established a unified mode for the whole processes based on multi-mode modeling methods, but the single mode can not accurately depict all operating modes. KOSANOVICH [13-15] pointed out that two obviously different modes should be separately established for data of each process with respective statistical characteristics, which can more accurately and efficiently monitor if abnormal conditions occurred. DONG and MCAVOY [16] also have verified Kosanovich’s point. On the basis of independent modeling, multi-mode problems were researched [17- 22] and each simple stable process has been modeled individually, and preferably monitoring effect was got. Soon after scholars put the idea of kernel function into principal component analysis to solve nonlinear problems; LEE et al [23] and CHOI [24] have done some research work for the nonlinear system fault identification. Combining KPCA with multi-way PCA, CHOI et al [24] and LEE et al [25] proposed an intermittent production process fault detection method and applied it to quality control of penicillin production process. With the development of process monitoring technologies, FLURY et al [26] proposed multi-group mode to detect multi-product batch processes. HWANG et al [27] proposed a super principal component analysis mode based on hierarchical clustering process for fault detection. Overall, these methods above concerned how to construct the model corresponding to each process mode more than modeling method of global and local features about multi-mode processes. As a matter of fact,in a production line, the operation modes can change for many reasons, but the process variables and the work principle is the same and some characteristics among the different modes are common, and each mode has its own unique and specific characteristics. For this idea, it is necessary to study the common and specific characteristics of industrial processes. ZHANG et al [28, 29] put forward multi-mode processes monitoring method based on subspace separation.
In order to fully analyze the multi-mode production processes, this work presents a novel multi-mode fault detection method. Compared with existing methods, this method not only can effectively separate the common and specific subspaces but also can adaptively adjust the parameters according to different actual working conditions, which enhances the reliability and robustness of the model. Experiment results show effectiveness of the proposed method.
2 Modeling and monitoring of multi-mode processes
For multi-mode processes, traditional monitoring methods are shown in Fig. 1. Since the correlations between mode and mode are neglected, the false alarms could be caused.
Different from the traditional methods, the monitoring methods based on subspace separation are shown in Fig. 2; the basic idea is that each mode is divided into the common subspace and specific subspace. In the common subspace, the process characteristics reflect global common information of each mode. In local specific subspace, the process characteristics reflect the variation information of each different mode.
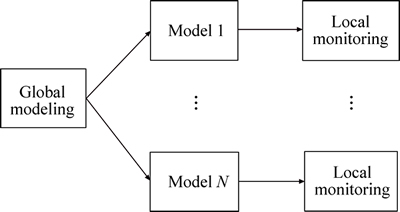
Fig. 1 Traditional multiple modeling method
In the proposed approach, it is considered that some features are relatively stable from one mode to another. Instead of isolating the effects of single mode, it is necessary to gain a detailed process-concerned insight into the potential mode characteristics from the multi-mode viewpoint, which can provide important information of the changeable process characteristics from one mode to another.
2.1 Modeling of multi-mode process based on KPCA
Suppose that multi-mode process, X1, X2, …,  is training data of k modes and Xd=[xd1, xd2, …, xdM], d=1, 2, …, k. Firstly, map data X to F space, that is
is training data of k modes and Xd=[xd1, xd2, …, xdM], d=1, 2, …, k. Firstly, map data X to F space, that is  so each mode datum can be represented as
so each mode datum can be represented as
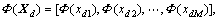
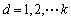
Solve the covariance matrix of each mode:
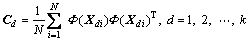 (1)
(1)
The principle component in 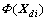 can be obtained by finding eigenvectors of Cd.
can be obtained by finding eigenvectors of Cd.

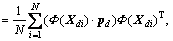
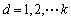 (2)
(2)
where · is dot product; λd denotes eigenvalues; pd is eigenvector of the covariance matrix Cd; d=1, 2, …, k. When 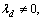 the principal component is spanned by
the principal component is spanned by
 (3)
(3)
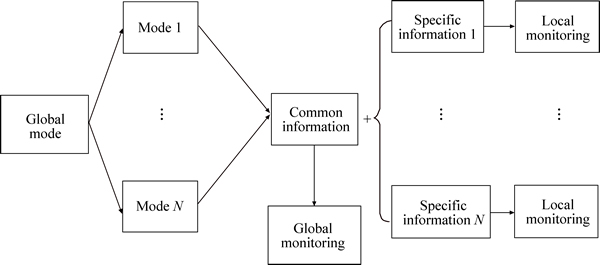
Fig. 2 Proposed method in this work Using kernel trick 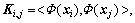 do left multiplication to Formula (2) simultaneously, and take Formula (3) into Formula (2), we can get:
do left multiplication to Formula (2) simultaneously, and take Formula (3) into Formula (2), we can get:
 (4)
(4)
All the eigenvalues are arranged in descendin  and corresponding coefficient factors are α1, α2, …, αM. Based on similarity theory, the comparison of feature vectors can be transformed into coefficient factor. The centered kernel matrix
and corresponding coefficient factors are α1, α2, …, αM. Based on similarity theory, the comparison of feature vectors can be transformed into coefficient factor. The centered kernel matrix 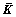 is calculated using the non-centered kernel matrix K:
is calculated using the non-centered kernel matrix K:

 (5)
(5)
where

So,kernel principal component can be got as follows:


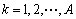 (6)
(6)
2.2 Multi-mode process monitoring based on similarity measure
2.2.1 Modeling of multi-mode common information subspace
By the method above, we obtained the similarity factor 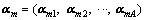 of any mode. Any two coefficient factor vectors of adjacent mode are denoted as
of any mode. Any two coefficient factor vectors of adjacent mode are denoted as  and
and 
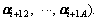
The distance between coefficient factor αi and αi+1 is expressed as
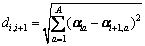 (7)
(7)
The cosine between coefficient factors αi and αi+1 is expressed as
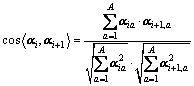 (8)
(8)
By integrating both distance measure and angle measure, a new similarity measure, Si,i+1, was proposed to improve the algorithm accuracy:
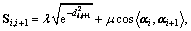
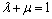 (9)
(9)
where λ and μ are weight parameters, and λ,  . The value of Si,i+1 is bounded between 0 and 1. When Si,i+1 approaches to 1, it indicates that αi resembles closely to αi+1.
. The value of Si,i+1 is bounded between 0 and 1. When Si,i+1 approaches to 1, it indicates that αi resembles closely to αi+1.
When Si,i+1=[ε, 1], two modal coefficient factors that belong to similar subspace are defined, where ε is the minimum threshold in similarity measure.
Then, measure the stage similar subspace factors with any other coefficient factor αj. And so on, measure n-1 times. The entire similar coefficient factor can be got by this way 
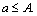
Then, the common characteristics between modes will be extracted, namely the load matrix of common characteristics:
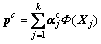 (10)
(10)
Common load matrix contains common variables correlation of each mode and reflects the common convert direction. Then, projecting the original data to common feature vector pc, we get score matrix of common subspace tc:
 (11)
(11)
Thus, the common information of each mode can be got:
 (12)
(12)
2.2.2 Modeling of multi-mode specific information subspace
Each mode datum consists of common and specific subspace information, and each mode datum can be expressed as
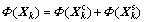 (13)
(13)
where represents common information subspace;
represents common information subspace;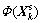 represents specific information subspace. So, specific characteristics of the load matrix ps can be got by excluding the common characteristics load ps from the load matrix p of each mode datum; ps reflects the specificity of each mode, which is the difference.
represents specific information subspace. So, specific characteristics of the load matrix ps can be got by excluding the common characteristics load ps from the load matrix p of each mode datum; ps reflects the specificity of each mode, which is the difference.
Corresponding to the above, coefficient factor αs specific features load matrix can be got by excluding the common coefficient factor αc from the integral coefficient factor α. According to the kernel principal component analysis, the specific subspace score matrix can be expressed as
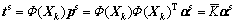 (14)
(14)
So, specific information portion of the data can be expressed as
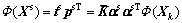 (15)
(15)
Specific subspace of each mode has its particularity and independence, which needs to be monitored separately. That is, model for each mode datum  separately. According to KPCA method, we can get:
separately. According to KPCA method, we can get:
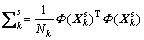
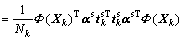 (16)
(16)
Transform the problem of covariance maximization into solving the eigenvalue and eigenvectors of 
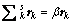 (17)
(17)
where β is eigenvalue; rk is the corresponding eigenvectors.
Eigenvectors can be defined as  , where jk is the coefficient factor of specific subspace. Then, the above equation is simplified to
, where jk is the coefficient factor of specific subspace. Then, the above equation is simplified to
 (18)
(18)
By singular value decomposition of the formula above, we can get jk and score vector 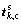 corresponding to the load vector:
corresponding to the load vector:
 (19)
(19)
where rk,c is 90% contribution rate part of load vector rk; jk,c is the corresponding coefficient factor;  is nuclear matrix after centralization. So, the estimator of
is nuclear matrix after centralization. So, the estimator of  can be expressed as
can be expressed as
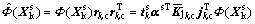 (20)
(20)
Residuals of specific subspace are:
 (21)
(21)
where rk,s is the remaining part of load vector rk; jk,s is the corresponding coefficient factor. So, specific information mode of each mode is:
 (22)
(22)
In summary, modeling of multi-mode fault detection method of common information subspace and specific information subspace based on the similarity has been completed.
2.3 Multi-mode process fault detection based on SM- KPCA
Use common subspace of the mode and the specific subspace of each mode for fault detection and then we can get a new datum  in multi-mode industrial process. The steps of multi-mode fault detection method based on similarity measure are as follows.
in multi-mode industrial process. The steps of multi-mode fault detection method based on similarity measure are as follows.
Step 1: Standardize sample data Xnew with mean and standard deviation of the modeling data:
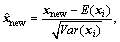 i=1, 2, …, N (23)
i=1, 2, …, N (23)
Construct a new kernel function 
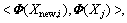 centralizing Knew, and then we got
centralizing Knew, and then we got 
We chose radial basis kernel function:
 (24)
(24)
Step 2: Obtain the common information of Φ(Xnew), calculate T-square(T2) statistic of common information subspace, denote the T2 statistic by 
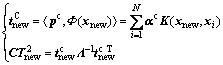 (25)
(25)
where Λ is a diagonal matrix constructed by the k eigenvalues of common eigenvectors of K. The control limit of T2 is calculated by
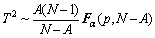 (26)
(26)
where Fα is an F distribution with degrees of freedom A and n-p with significance level α.
If the statistic calculation over the calibration control line, we consider the common information subspace abnormal; otherwise, the monitoring process is in a normal state.
Step 3: Obtain the specific information of Φ(Xnew), calculate T-square statistic of specific information subspace, denote the T2 and SPE statistic by  and SSPEnew:
and SSPEnew:
 (27)
(27)
The control limit of SPE is obtained by
 (28)
(28)
where
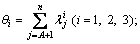
 (29)
(29)
If any statistics calculated are beyond the calibration control limits, we consider the monitoring process works abnormal; otherwise, the monitoring process is in a normal state.
In summary, the method of multi-mode process monitoring based on SM-KPCA has been completed.
3 Simulation and result analysis
3.1 Introduction of mill grinding process
Grinding is an important step in ore dressing process. The purpose of ore dressing production is to get the effective mineral ingredients to make all kinds of mineral ores separate from each other, and then sort out the useful mineral products. Among them, the product index in grinding process directly affects the utilization of mineral and the recovery of resources which has a significant impact on the economic benefits of concentrator.
In the process of grinding, system puts primary crushed ore into the ball mill by adjusting its feeder, and a certain percentage of water and steels balls are added at the same time. After rotating, the ball mill discharges slurry and pours slurry into the mine pool. The slurry in ore tank is sent to hydro-cyclone by ore pump for grading. If the pulp satisfies the standard, it will be sent to the next step. On the contrary, it will be returned to the ball mill and grind again. The flowchart of the whole technological grinding craft process is shown in Fig. 3.
From Fig. 3, regardless of the ore grinding process, the whole process mainly contains two parts which are slime dam and hydro-cyclones. In the selection process, the liquid level of the slime dam is requested to be stable, which is controlled by the moisturizing. If the ball mill is abnormal, the density of the ore pulp will be changed which can lead to the variety of the liquid level. The hydro-cyclone contains three important variables including concentration and pressure of hydro-cyclones, and overflow granularity. The overflow granularity is the target of production, which will be influenced by the variables in slime dam and hydro-cyclones. Though the two parts are relatively independent, they influence each other and restrict each other.
During the selection process, the common faults mainly include the following five parts: pressure of hydro-cyclones, feed concentration of hydro-cyclones, liquid level of slime dam, supplementary water of slime dam, overflow particle size of hydro-cyclones. The occurring phenomena and the possible reasons for these malfunctions are listed in Table 1.
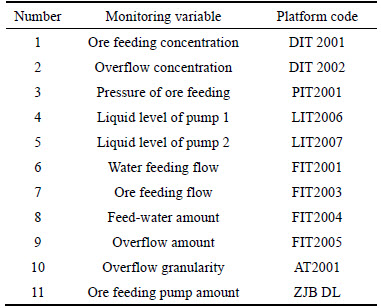
According to Fig. 3 and Table 1, when monitoring the ore grinding process, the variables can be selected out. In our monitoring experiment, the monitoring variables include:ore feeding concentration (DIT2001), ore feeding pressure (PIT2001), liquid level (LIT2006&2007), water and ore feeding flow (FIT2001&2003), amount of feed-water and overflow (FIT2004&2005) , overflow granularity (AT2001) and amount of ore feeding pump(ZJB DL). Measurable variables in mill grinding process are shown in Table 2.
In the actual process of grinding, the diversity of the ore leads to different ore feeding amounts. When the quantity changes, some of the measured variables will be changed and system will work at multi-mode processes. Then, the whole process can be monitored by the proposed method.
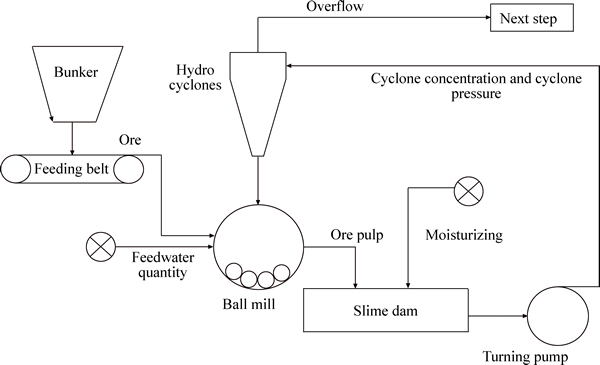
Fig. 3 Flowchart of ore grinding craft process
Table 1 Phenomena and reasons for malfunctions
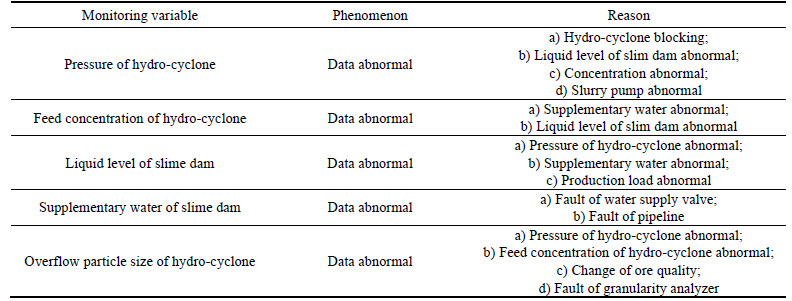
Table 2 Measurable variables in mill grinding process
3.2 Offline modeling in mill grinding
In the modeling process, taking into account the process which works in two modes, we can adjust angle and distance weight parameters λ, μ and the minimum threshold ε in similarity measure to make the number of common and specific subspace similarity factors equal, that is to make the two subspace own the same amount of projection direction. The influence of angle and distance weight parameters λ, μ in similarity measure on process monitoring will be discussed. In the offline modeling phase, we aim to find suitable distance and angle weight values which match the working conditions in the process of grinding and classification. Particular way is as follows: select offline training data of multi-mode for modeling; use normal data of Mode One as test data and common features model for the simulation test. Two weight parameters λ, μ are both in 0-1, and during testing we chose the step as 0.1, that is, we chose 11 different sets of weights.
During the process of solving the minimum threshold, our principle is to make the public space and the special space at the same dimension, that is, to make public and special space with the same number of projection directions to determine the smallest threshold ε. And then calculate the false alarm rate under different conditions; select the most suitable as well as the lowest false alarm rate weight values for on-line monitoring. Monitoring results from different distances and angles are shown in Fig. 4. The false alarm rate corresponding to different weights of public space modal is shown in Table 3. From Fig. 4 and Table 3, we can conclude that when distance weighting coefficient μ changes from 0 to 0.8, the false alarm rate changes from 15.25% to 2.5%, and when μ changes from 0.8 to 1.0, the false alarm rate changes from 2.5% to 11.75%. So, we choose μ=0.8 as the online monitoring distance weight coefficient under this working conditions.
3.3 Online modeling in mill grinding
According to the results of offline modeling, we set the various parameters. First we use common space mode for monitoring in mill grinding process, and the T2 statistic of test data in the common subspace of the detection is shown in Fig. 5. We can see that the T2 statistic in the vicinity of 290 sampling points exceeds the control limits. That is, failure began to appear from this time point. In this way, the faults can be promptly found in multi-mode processes.
Then, we use specific subspace of mode 1 for monitoring. The T2 and SPE in Mode 1 are shown in Figs. 6 and 7.
From Fig. 6 and Fig. 7, we can get the T2 and SPE statistics which do not exceed the control limits at previous 290 sampling points. After 290 sampling points the two statistics both exceed the control limits. We can conclude that before the 290th point system operates in normal state of Mode 1.
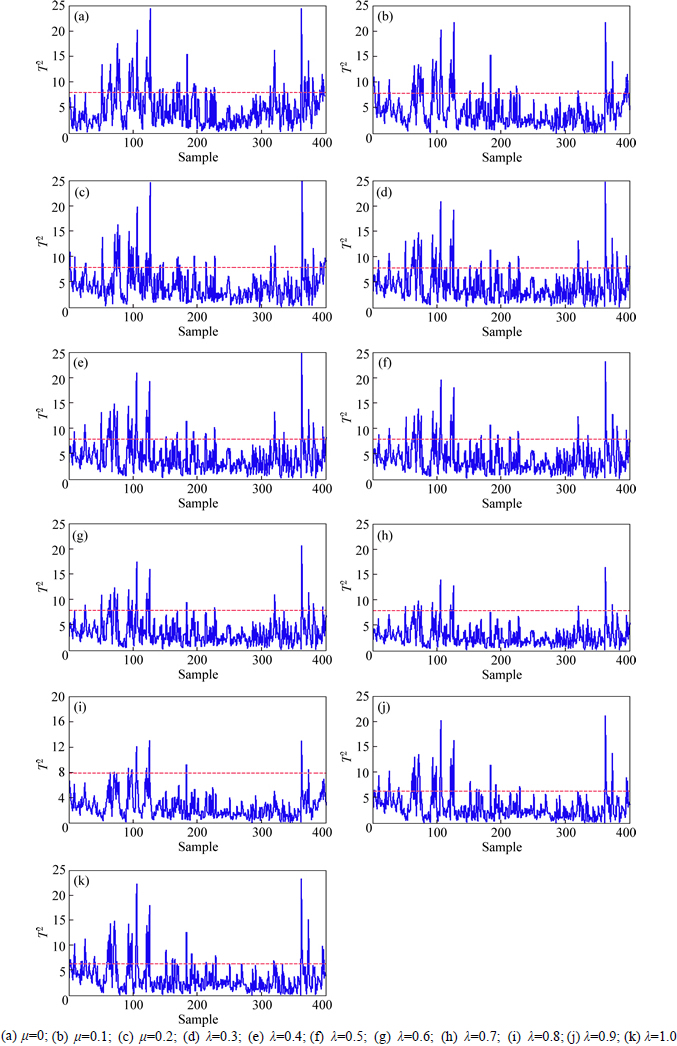
Fig. 4 Offline T2 statistic of common subspace in mill grinding process:
Table 3 False alarm rate corresponding to different weights


Fig. 5 Online T2 statistic of common subspace in mill grinding process
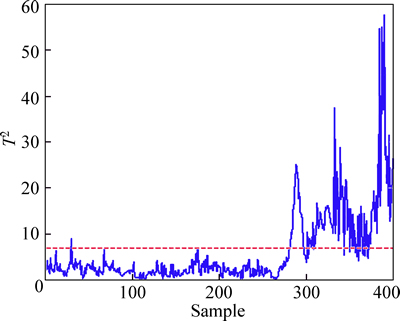
Fig. 6 Online T2 statistic of specific subspace 1 in mill grinding process
Then, we use specific subspace of Mode 2 for monitoring, and the T2 and SPE statistics of specific subspace in Mode 2 are shown in Figs. 8 and 9.
The results show that most of the 400 samples exceed the control limits. That is, before the faults occur, system does not work in the normal state of Mode 2.

Fig. 7 Online SPE statistic of specific subspace 1 in mill grinding process

Fig. 8 Online T2 statistic of specific subspace 2 in mill grinding process
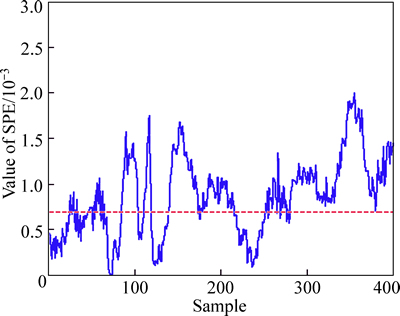
Fig. 9 Online SPE statistic of specific subspace 2 in mill grinding process
In addition, aimed at above mill grinding process, Fig. 10 shows the monitoring results based on KPCA. Process monitoring results comparison is shown in Table 4. Comparison results show that the method of SM-PCA is a novel monitoring scheme of complex multi-mode process.
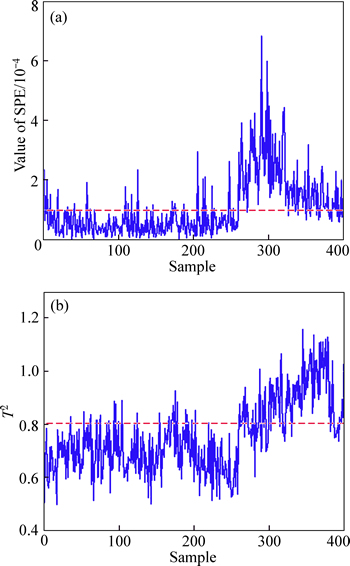
Fig. 10 Online SPE statistic of KPCA in mill grinding process (a) and online T2 statistic of KPCA in mill grinding process (b)
Table 4 Contrast of monitoring result using SM-KPCA and KPCA method separately

4 Conclusions
In this work, a new method was proposed for monitoring of multi-mode processes, which can separate correctly common subspace and specific subspace. Not only the method can effectively monitor faults but it can also find which mode the process works in before the faults occur. Moreover, in offline modeling phase, this method can decide the optimal parameters which adapt to current conditions. That will enhance the reliability and robustness of the monitoring program. What’s more, considering the nonlinearity of process data, the kernel trick is introduced into the proposed method, which can deal with the complex process monitoring problem. The effectiveness and practicability are proven by the real mill grinding process.
References
[1] CHAMPAGNE M, DUDZIC M. Industrial use of multivariate statistical analysis for process monitoring and control [C]// Proceedings of the American Control Conference. Anchorage, 2002(1): 594-599.
[2] WANG Li, SHI Hong-do. Multivariate statistical process monitoring using an improved independent component analysis [J]. Chemical Engineering Research & Design, 2010, 88(4A): 403-414.
[3] LOUWERSE D J, SMILDE A K. Multivariate statistical process control of batch processes based on three-way models [J]. Chemical Engineering Science, 2000, 55: 1225-1235.
[4] GE Zhi-qing, SONG Zhi-huan, GAO Fu-rong. Review of recent research on data-based process monitoring [J]. Industrial & Engineering Chemistry Research, 2013, 52 (10): 3543-3562.
[5] CHIANG H L, RUSSELL E L, BRAATZ R D. Fault detection and diagnosis in industrial systems [M]. New York: Springer, 2001.
[6] NOMIKOS P, MACGREGOR J F. Monitoring batch processes using multiway principal component analysis [J]. AIChE J, 1994, 40: 1361-1375.
[7] CHO J H, LEE J M, CHOI S W, LEE Dong-kwon. Fault identification for process monitoring using kernel principal component analysis [J]. Chemical Engineering Science, 2005, 60(1): 279-288.
[8] CHENG Chuu-yuan, HSU Chun-chin, CHEN Mu-chen. Adaptive kernel principal component analysis (KPCA) for monitoring small disturbances of nonlinear processes [J]. Industrial & Engineering Chemistry Research, 2010, 49(5): 2254-2262.
[9] SUMANA C, BHUSHAN M, VENKATESWARLU C, GUDI R D. Improved nonlinear process monitoring using KPCA with sample vector selection and combined index [J]. Asia-Pacific Journal of Chemical Engineering, 2011, 6(3): 460-469.
[10] DAI Chen-xi, LIU Zhi-gang, CUI Yan. The transformer fault diagnosis combing KPCA with PNN [C]// 2014 International Joint Conference on Neural Networks. Beijing: IEEEXplore, 2014: 1314-1319.
[11] HWANG D H, HAN C H. Real-time monitoring for a process with multiple operating modes [J]. Control Engineering Practice, 1999, 7: 891-902.
[12] LANE S, MARTIN E B, KOOIJMANS R, MORRIS A J. Performance monitoring of a multi-product semi-batch process [J]. Process Control, 2000, 11(1): 1-11.
[13] KOSANOVICH K A, PIOVOSO M J, DAHL K S. Multi-way PCA applied to an industrial batch process [C]// Proc of American Control Conference. Maryland: IEEE, 1994: 1294-1298
[14] KOSANOVICH K A, DAHL K S, PIOVOSO M J. Improved process understanding using multiway principal component analysis [J]. Ind Eng Chem Res, 1996, 35(1): 138-146.
[15] MA He-he, HU Yi, SHI Hong-do. A novel local neighborhood standardization strategy and its application in fault detection of multimode processes [J]. Chemometrics and Intelligent Laboratory Systems, 2012, 118(15): 287-300.
[16] DONG Dong, MCAVOY T J. Multi-stage batch process monitoring [C]// Proc. of American Control Conf. Washington: IEEEXplore, 1995, 3: 1857-1861.
[17] BHAGWAT A, SRINIVASAN P, KRISHNASWAMY P R. Multi-linear model-based fault detection during process transitions [J]. Chemical Engineering Science, 2003, 58: 1649-1670.
[18] NG Y S, SRINIVASAN R. An adjoined multi-model approach for monitoring batch and transient operations [J]. Computers and Chemical Engineering, 2009, 33: 887-902.
[19] DOAN X T, SRINIVASAN R. Online monitoring of multi-phase batch processes using phase-based multivariate statistical process control [J]. Computers and Chemical Engineering, 2008, 32: 230-243.
[20] CHEN J H, LIU J L. Mixture principal component component analysis models for process monitoring [J]. Industrial & Engineering Chemistry Research, 1999, 38(4): 1478-1488.
[21] ZHAO Shi-jian, ZHANG Jie, XU Yong-mao. Monitoring of processes with multiple operating modes through multiple principal component analysis models [J]. Industrial & Engineering Chemistry Research, 2004, 43(22): 7025-7035.
[22] ZHAO Shi-jian, ZHANG Jie, XU Yong-mao. Performance monitoring of processes with multiple operating modes through multiple PLS models [J]. Process Control, 2006, 16(7): 763-772.
[23] LEE J M, YOO C K, SANG W C, VANROLLEGHEM D A, LEE I B. Nonlinear process monitoring using kernel principal component analysis [J]. Chemical Engineering Science, 2004, 59(1): 223-234.
[24] SANG W C, LEE C, LEE J M, JIN H P, LEE I B. Fault detection and identification of nonlinear processes based on kernel PCA [J]. Chemometrics and Intelligent Laboratory Systems, 2005, 75(1): 55-67.
[25] LEE J M, YOO C, LEE I B. Fault detection of batch processes using multi-way kernel principal component analysis [J]. Computers and Chemical Engineering, 2004, 28(91): 1837-1847.
[26] FLURY B K. Two generalizations of the common principal component model [J]. Biometrika, 1987, 74(1): 59-69.
[27] HWANG D H, HAN C. Real-time monitoring for a process with multiple operating modes [J]. Control Engineering Practice, 1999, 7(7): 891-902.
[28] ZHANG Ying-wei, LI Shuai. Modeling and monitoring of nonlinear multi-mode processes [J]. Control Engineering Practice, 2014, 22: 194-204.
[29] ZHANG Ying-wei, ZHANG Hai-long. Data-based modeling and monitoring for multimode processes using local tangent space alignment [C]// Computer Science. Shenyang: 2012, 7367: 169-178.
(Edited by YANG Hua)
Cite this article as: WANG Xiao-gang, HUANG Li-wei, ZHANG Ying-wei. Modeling and monitoring of nonlinear multi-mode processes based on similarity measure-KPCA [J]. Journal of Central South University, 2017, 24(3): 665-674. DOI: 10.1007/s11771-017-3467-z.
Foundation item: Projects(61273163, 61325015, 61304121) supported by the National Natural Science Foundation of China
Received date: 2015-11-13; Accepted date: 2016-01-13
Corresponding author: WANG Xiao-gang, PhD, Associate Professor; Tel: +86-13898828491; E-mail: wangxiaogang@mail.neu.edu.cn