J. Cent. South Univ. (2019) 26: 719-727
DOI: https://doi.org/10.1007/s11771-019-4042-6
Lithological classification of cement quarry using discriminant algorithms
Bulent TUTMEZ
Department of Mining Engineering, Inonu University, Malatya 44280, Turkey
Central South University Press and Springer-Verlag GmbH Germany, part of Springer Nature 2019
Abstract: As such in any industrial raw material site characterization study, making a lithological evaluation for cement raw materials includes a description of physical characteristics as well as grain size and chemical composition. For providing the cement components in accordance with the specifications required, making the classification of the cement raw material pit is needed. To make this identification in a spatial system at a quarry stage, the supervised pattern recognition analysis has been performed. By using four discriminant analysis algorithms, lithological classifications at three levels, which are with limestone, marly-limestone (calcareous marl) and marl, have been made based on the main chemical components such as calcium oxide (CaO), alumina (Al2O3), silica (SiO2), and iron (Fe2O3). The results show that discriminant algorithms can be used as strong classifiers in cement quarry identification. It has also recorded that the conditional and mixed classifiers perform better than the conventional discriminant algorithms.
Key words: cement; discriminant analysis; lithology classification; quarry identification
Cite this article as: Bulent TUTMEZ. Lithological classification of cement quarry using discriminant algorithms [J]. Journal of Central South University, 2019, 26(3): 719–727. DOI: https://doi.org/10.1007/s11771-019-4042-6.
1 Introduction
As a powder material, cement is blended with water, form in plastic mass, easy to shape, adjusting with time and hardening gradually with strength increase [1]. Cement composition is the fundamental for partition of cements into kinds such as Portland, Slag and Pozzolanic. Due to the technological specifications, cement production requires to prepare necessary composition from the chemicals and other parameters. Thus, the material of designed phase composition is the main objective of the clinkering (Portland cement clinker) process [2]. Although the chemical composition of clinker has a complexity, the sum of four main ingredients, CaO, SiO2, Al2O2 and Fe2O3 is as a general higher than 95%. Therefore, the identification of these components both in factory and quarry should be drawn attention.
In general, a lithological evaluation for a raw material is a description of its physical characteristics such as texture, grain size, or composition. Appraising the distribution of chemical composition in a cement raw material quarry is essential to provide uniform sources for production. As discussed in Refs. [3, 4], maintaining the quality of cement production is possible only if the raw mix possesses ideal composition and furthermore if classification of this composition has successfully been made. Therefore, identifying and/or classifying the cement raw material pits are critical steps in planning stages. Recently, an optimization study was conducted to identify raw materials in a quarry used in cement production stage [5].
The principal motivation of a supervised pattern recognition analysis, also known as classification, is to obtain a structure that yields the optimal discrimination between several classes [6].This recognition also has critical importance in cement raw material preparation. Although many studies have discussed the distribution of the raw materials in a cement stone pit [7, 8], a comparative classification analysis by different classifiers is required.
There have recently been published some novel works as a discriminant analysis/function- based spatial field studies [9–11]. Recently, a stability classification model for mine-lane surrounding rock was established using distance discriminant analysis [12]. Although use of discriminant analysis-based cement quarry classification has a potential application and to gain insight into relationship and distribution at the site conditions is important, there is a gap in literature on this topic. With the exception of having good predictive capability, a reliable classification method also obtains insight in what distinguishes different classes from each other [13]. To give some insights to the components and filling the gap in the literature, conventional and novel (mixed) discriminant models have been examined in this study and the results have been discussed.
2 Methodology
2.1 Cement chemistry and principal components
A computational case study in a cement stone pit requires the determination of spatial field parameters as well as chemical measurements. Because chemical parameters based on the oxide composition are very useful in describing clinker characteristics, spatial evaluations of the components in the field scale gains a paramount importance [14]. In a cement production process, the principal need to provide an acceptable raw mix is calcium oxide (CaO). The secondary components are desired to obtain a balance of alumina (Al2O3), silica (SiO2), and iron (Fe2O3). For acquiring the balance of main oxides, the lime saturation factor (FLS), silica ratio (RS), and alumina ratio (RA) are utilized as the conventional indexes:
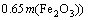(1)
(2)
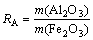(3)
A long-termed production planning of cement pit is primarily concerned with developing a map and classified components based on spatial coordinates. By this way, controlling the inputs of a clinker can be maintained by the practitioners.
2.2 Discriminant analysis (DA)
A linear regression analysis expects that the response variable Y is quantitative. However, in some situations the target variable is instead qualitative. At this situation, in order to predict qualitative targets, classification is utilized. Among the well-known classifiers, the superiority of DA has been discussed in Ref. [15]. For example, when the classes are well-separated, DA models provide better parameter estimations. Similarly, if number of data is small and distribution of predictors X is nearly normal, DA models can be more stable than the other models such as logistic regression and K-nearest neighbours.
2.2.1 Linear discriminant analysis (LDA)
Normal distribution for the individual classes is considered in conventional discriminant analysis. In this method, the probability parameters, μ1, …, μK, π1, …, πK, and σ2, are defined. For these parameters, the LDA algorithm applies the Bayes classifier via plugging predictions [16]. The first required estimates are:
(4)
(5)
where nk denotes the number of training data in the kth class. The LDA classifier tries to make a class large as
(6)
In Eq. (6), a measurement is assigned as X=x and class membership probability is found as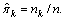 
In the case of multiple independent variables X=(X1, X2, …, Xp), a multivariate Gaussian distribution is used. To obtain this distribution, a class-specific mean vector and a common covariance matrix N(μk, Σ) are calculated. The vector/matrix version of Eq. (6) can be expressed as [15]
(7)
2.2.2 Quadratic discriminant analysis (QDA)
In LDA algorithm, the measurements within each class are benefited from a multivariate Gaussian distribution with a class-specific mean vector and a covariance matrix. Similar to LDA, QDA classifier employs Gaussian distribution and Bayes’s theorem to make some predictions. The main difference is to consider the variability. Differently from LDA, QDA algorithm calculates different covariance matrixes for each class X~N (μk, Σk). In QDA, the Bayes classifier specifies a measurement X=x to the class [17]. The following expression aims to provide a largest class:
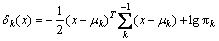
(8)
Unlike Eq. (7), the x materializes as a quadratic function in Eq. (8). In practice, QDA is recommended if the training set is large
2.2.3 Combined discriminant analysis methods
The conventional LDA algorithm has some virtues such as simple prototyping and optimal low dimensional views. However, lots of data and correlated predictors (noisy coefficients) are the main limitations of this technique [16]. On a similar axis, although QDA has superiority in the case of non-normally distributed data, observations may be not well described using the individual covariance matrices. As a consequence, there are relatively new conditional algorithms such as flexible (FDA) and model-based (mixed) (MBDA) discriminant analysis methods were suggested [18].
The basics of FDA method were formulated by HASTIE et al [19]. FDA was developed as the nonparametric structure of discriminant analysis by substituting linear regression. The method amounts to expanding/selecting the predictors using basis transformations chosen by regression. Thus, the penalized LDA is addressed in a new space.
In especial, MBDA concentrates on class densities. Each class can be specified with a mixture of normal distributions, and then assign an object to the class for which the overall mixture density is the maximal. In this way, for every class several means and covariance matrices are estimated. After that, one of them is selected. It is clear that this algorithm can only be employed when the ratio of objects to variables is very large [20].
3 Experimental
3.1 Site and data set
The cement open pit in Adana, Turkey was examined in the case study. In our former work, the relationships in this site have been explored by regression-based algorithms [21]. Although the original data include 67 observations, in five locations some of the chemical values were not recorded. Therefore, 60 boreholes have been considered. The data set consisting of 60 observations was randomly divided into two subsets: the training set (80%, 48 samples) and the testing set (20%, 12 samples), respectively.
The lithological content of the quarry is taken place with limestone, marly-limestone (calcareous marl) and marl. In this study, the classifications of the quarry based on the lithological variability are made by different discriminant algorithms.Figures 1 and 2 illustrate the scatter plots of coordinates and chemical components, respectively. As seen in Figure 1, there are no big skewed distributions for the coordinates. In Figure 2, although Ca values show weak negative (left-skewed) skewness, the other chemical components (Si, Al and Fe) illustrate weak positive (right-skewed) distribution. From a general view, no big statistical problem has been recorded for a potential parametric evaluation.
3.2 Results and discussion
To describe that the correlations among the components have critical importance for the future classification analyses, all the discriminant methods use covariance structures and multivariate densities. Figure 3 gives the correlations between the chemical components obtained by training data. In compliance with the LSE in Eq. (1), reverse relationships are recorded between Ca and other components.
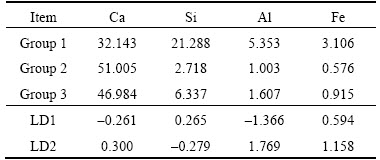
All the case studies have been performed to identify the site on the ground of three different lithological characters. In the LDA-based implementation, with a class-specific mean vector and a common covariance matrix the observations within each class have been obtained from multivariate Gaussian distribution with the number of predictors p=4. Class means and coefficients of linear discriminants are summarized in Table 1. Figure 4 shows the obtained classification performed using training data and the LD classifier.
Figure 1 Scatter plot for coordinates
To focus on the performance of the LDA classifier, the model parameters have been used to classify the test data. As seen in Table 2, one of twelve observations has been misclassified. The estimated error for the testing set can be calculated as 1/12=0.083.
Histogram of the testing set is given in Figure 5. Although the number of data sets in testing work is very limited, a successful discrimination has been recorded. The results are illustrated by using Si and Al in Figure 6. Applying an 80% threshold to the posterior probabilities provides the following outcomes:
3 observations for p≥0.8%
and
9 observations for p<0.8.
In the QDA-based discriminant analysis, the output comprises of the group means which have been the same as given in Table 1. However, it does not include the coefficients of the LDs, since the QDA classifier covers a quadratic, rather than a linear, function of the predictors as discussed in Ref.[15].The test performance of the QDA classifier is illustrated based on Al and Si variables as in Figure 7. In this application, only one measurement, [8.39, 1.27], has been misclassified. Therefore, the estimated error for the testing set has been calculated as 1/12=0.083.
Figure 2 Scatter plot for chemical components
In the third application, the FDA classifier was used. Based on the transformations, the algorithm has classified the observations using a new space and the canonical variables. The resulting application for test data is given in Figure 8. The FDA classifier has produced very low error variances (eta squares). In terms of a variance analysis perspective, if there is no variability in the classification, 100% of the variance should be explained by the treatment. This value has been materialized as 97.57% for Var 1 and 100% for Var 2, respectively.
Figure 3 Correlations between chemical components
Table 1 Group means and coefficients of LD1 and LD2
In the fourth application, the MBDA classifier has been practiced. With a mixture of normal distributions, first each class was identified; then the observations have been assigned to the suitable classes for which the overall mixture density has been maximal. Figure 8 illustrates the classification on the testing data sets. It can be seen in Figure 9,the MBDA algorithm has made very successful classification.
Figure 4 LDA-based classification for training data
Table 2 Classification matrix for test data
Figure 5 Histogram of testing LDA classification:
The results show that the LDA and QDA classifiers revealed similar performance. Although the FDA classifier performed better classification from these conventional approaches, the best performance has been provided by the MBDA-based classification. The MBDA algorithm concentrates on the class densities and this mixed model enables to provide several means and covariance matrices as a meta-data. Finally, it has been recorded that the mixed model is suitable when the ratio of the observations to variables is large.
Figure 6 LDA-based classification for testing data
Figure 7 QDA-based classification for testing data
Figure 8 FDA-based classification for testing data
Figure 9 MBDA-based classification for testing data
4 Conclusions
Making an appraisal on the lithology of quarry using the main components of cement has a critical importance in planning the inputs of a clinker.Lithological classification of a cement quarry has been made at three levels based on the main chemical components: calcium oxide (CaO), alumina (Al2O3), silica (SiO2), and iron (Fe2O3). For this purpose, the conventional and the novel (mixed) classification algorithms were utilized.
The outcomes of the algorithms revealed that discriminant algorithms can be used as strong classifiers in cement quarries. It has also been recorded that the conditional (FDA) and the mixed (MBDA) classifiers performed better than the conventional discriminant algorithms such as the LDA and the QDA.
References
[1] AZADEGAN O, LI J, JAFARI S H. Estimation of shear strength parameters of lime-cement stabilized granular soils from unconfined compressive tests [J]. Geomechanics and Engineering, 2014, 7(3): 247–261.
[2] KURDOWSKI W. Cement and concrete chemistry [M]. New York: Springer, 2014.
[3] ONUR A H, KONAK G, KARAKUS D. Limestone quarry quality optimization for a cement factory in Turkey [J]. J South Afr Inst Min Metall, 2008, 108(12): 753–757.
[4] TUTMEZ B. Analyzing non-stationarity in cement stone pit by median polish interpolation: A case study [J]. Journal Applied Statistics, 2013, 41(2): 454–466.
[5] JOSHI D, CHATTERJEE S, EQUEENUDDIN SkMd. Limestone quarry production planning for consistent supply of raw materials to cement plant: A case study from Indian cement industry with a captive quarry [J]. Mineral Mining Technology, 2015, 51(5): 980–992.
[6] BRAMER M. Principles of data mining [M]. London: Springer-Verlag, 2016.
[7] ASAD M W A. Implementing a blending optimization model for short-range production planning of cement quarry operation [J]. J Min Sci, 2010, 46(5): 525–535.
[8] KARAKUS D. Raw material homogenization production plan in multiple quarries-slope stability assessment: Cement raw material clay pit sample [J]. Journal of Mining Science, 2012, 48(1): 154–166.
[9] AGHA M, FERRELL R E, HART G F. Mineralogy of Egyptian bentonitic clays I: Discriminant function analysis [J]. Clays and Clay Minerals, 2012, 60(4): 387–404.
[10] KUYUK H S, YILDIRIM E, DOGAN E. Clustering seismic activities using linear and nonlinear discriminant analysis [J]. Journal of Earth Science, 2014, 25(1): 140–145.
[11] GHANNADPOUR S S, HEZARKHANI A. Exploration geochemistry data-application for anomaly separation based on discriminant function analysis in the Parkam porphyry system (Iran) [J]. Geosciences Journal, 2016, 20(6): 837–850.
[12] ZHANG W, LI X B, GONG F G. Stability classification model of mine-lane surrounding rock based on distance discriminant analysis method [J]. Journal of Central South University, 2008, 15: 117–120.
[13] ADACHI K. Matrix-based introduction to multivariate data analysis [M]. New York: Springer, 2016.
[14] TSAKIRIDIS P E, SAMOUHOS M, PEPPAS A. Silico- aluminous bottom ash valorization in cement clinker production: Synthesis, characterization and hydration properties [J]. Construction and Building Materials, 2016, 126: 673–681.
[15] JAMES G, WITTEN G, HASTIE T, TIBSHIRANI R. An introduction to statistical learning [M]. New York: Springer, 2013.
[16] HASTIE T, TIBSHIRANI R, JAMES G, FRIEDMAN J. The elements of statistical learning [M]. New York: Springer, 2009.
[17] SRIVASTAVA S, GUPTA M R, FRIGYIK B A. Bayesian quadratic discriminant analysis [J]. Journal of Machine Learning Research, 2007, 8: 1277–1305.
[18] FRALEY C, RAFTERY A E. Model-based clustering, discriminant analysis, and density Estimation [J]. Journal of the American Statistical Association, 2002, 97: 611–631.
[19] HASTIE T, TIBSHIRANI R, BUJA A. Flexible discriminant analysis by optimal scoring [J], Journal of the American Statistical Association, 1994, 89(428): 1255–1270.
[20] WEHRENS R. Chemometrics with R [M]. Heidelberg: Springer, 2011.
[21] TUTMEZ B, DAG A. Regression-based algorithms for exploring the relationships in a cement raw material quarry [J]. Computers and Concrete, 2012, 10(5): 457–467.
(Edited by DENG Lü-xiang)
中文导读
基于识别算法的水泥矿山岩性分析
摘要：在任何工业原料场地特征的研究中，对水泥原材料进行岩性评价的研究均包括其物理特征、粒度和化学组成的相关描述。为了按照要求规格提供水泥组分，需要对水泥原料坑进行分类。采用监督模式识别分析法在采石场阶段的空间系统中进行识别。通过使用四种识别分析算法，基于主要化学成分如氧化钙（CaO）、氧化铝（Al2O3）、二氧化硅（SiO2）和铁（Fe2O3），在石灰石，泥灰质石灰岩（钙质泥灰岩）和泥灰岩三个层面进行岩性分类。结果表明：识别算法可以作为水泥采石场识别中的强分类器，而且该条件和混合分类器比传统的识别算法效果更好。
关键词：水泥；识别分析；岩石学；矿山
Received date: 2017-04-18; Accepted date: 2018-11-10
Corresponding author: Bulent TUTMEZ, PhD, Professor; Tel: +90-4223774773; E-mail: bulent.tutmez@inonu.edu.tr; ORCID: 0000- 0002-2618-3285
