兆瓦级风电机组风力桨叶多学科设计优化
刘冠麟1, 2,鄂加强1,张彬1
(1. 湖南大学 机械与运载工程学院,湖南 长沙,410082;
2. 湖南涉外经济学院 机械工程学院,湖南 长沙,410205)
摘要:为了提高兆瓦级风电机组风力桨叶整体性能,以兆瓦级风电机组风力桨叶气动性能、质量、桨片根部的极限推力和噪声水平为目标函数建立多学科设计优化模型,并充分考虑各学科之间的耦合效应,采用自适应混沌优化算法对多学科设计优化模型进行求解。研究结果表明:兆瓦级风电机组风力桨叶风能利用系数Cp增加12.5%,质量M 减小11.00%,桨叶根部的极限推力载荷F减少12.60%,噪声Sptotal减小10.48%;兆瓦级风电机组风力桨叶翼型的升力系数和气动性能得到了较大优化。
关键词:风力桨叶;多学科优化设计;混沌优化算法;气动性能
中图分类号:TM614;TK83 文献标志码:A 文章编号:1672-7207(2013)01-0140-09
Multidisciplinary optimization design on blades of MW wind turbine
LIU Guanlin1, 2, E Jiaqiang1, ZHANG Bin1
(1. College of Mechanical and Vehicle Engineering, Hunan University, Changsha 410082, China;
2. School of Mechanical Engineering, Hunan International Economics University, Changsha 410205, China)
Abstract: In order to improve the whole performance of the blades of MW wind turbine, a multidisciplinary design optimization (MDO) model was established based on objective function such as aerodynamic performance, mass, blade root thrust and the level of noise. Based on the coupled effect between each subject, the blades of MW wind turbine were designed by using MDO based on self-adaptive chaotic optimization algorithm. The results show that for the blades of MW wind turbine, power coefficient increase by 12.50%, mass reduces by 11.00%, blade root thrust reduces by 12.60%, and the level of noise reduces by 10.48%. The lift coefficient and aerodynamic performance are greatly optimized.
Key words: blades of wind turbine; multidisciplinary optimization design; self-adaptive chaotic optimization algorithm; aerodynamic performance
桨叶是风力发电机的关键部件之一。目前,风电机组风力桨叶的研制正向大型化、低成本、高性能、轻量化发展[1-3],其总体质量直接影响到风力发电机的效率、寿命和性能等。桨叶的气动性能和结构动力学性能直接影响着风力机的运行情况。气动特性直接影响风力机能否充分利用风能,因而,在设计时,必须尽量使桨叶具有较高的风能利用系数,从而很好地用于发电[4]。结构动力学特性也是风力机设计中比较关心的因素,因为风电机组风力桨叶在旋转过程中很难避免由于惯性不平衡或者失速引起的激振力,激振力就有可能引起系统共振,从而导致叶片发生断裂。兆瓦级风电机组风力桨叶的强度、刚度、疲劳寿命、振动和可靠性设计方面与国外的相比还存在一定差距[5-6]。尽管国外已将计算流体力学、有限元和结构动力学分析、新型的信息管理与应用技术应用于风力机的设计、应用与实际操作,但风力机的设计还停留在“设计—试制—试验—改进”阶段,实用性较差,尽管对存在的问题和故障现象提出一些解决办法,但都未从根本上解决存在的问题,仍然存在成本较高和使用寿命较短等缺点;此外,目前桨叶的设计方法除了传统设计方法以外,还有其他一些优化设计方法[7],但这些优化设计方法只对单一目标进行优化,并没有考虑包含多个优化目标的多学科优化[8-9]。因此,必须研究开发性能好、工作可靠的桨叶,就要从气动设计、构造设计和结构设计等方面综合地进行多学科优化,以满足环境恶劣、工况多变的条件,以便为开发稳定、高寿命的兆瓦级风电机组风力桨叶提供有效、可靠的理论设计方法,这样,不但能为兆瓦级风电机组风力桨叶及风轮的动力性能改善和总体优化提供依据,而且对独立开发新型风力发电机组浆叶具有一定的应用价值。
1 兆瓦级风电机组风力桨叶翼型和结构
风力机的效率主要由桨叶决定,而桨叶翼型作为桨叶的基本要素,其几何形状即几何特性决定了它的空气动力特性。
最常用且最具代表性的传统风力机翼型为NACA翼型。翼型也叫翼剖面,是指用垂直于叶片长度方向的平面去截叶片而得到的截面形状。翼型的几何特征如图1所示。图1中:B为翼型的后缘;A为前缘;直线段AB为翼弦;AB的长度为弦长c;弧面AMB为上翼面;弧面ANB为下翼面;翼弦的各垂线被翼型的上、下表面型线所截得的各线段中最大者(即最大厚度)为翼型的厚度t。风力桨叶的结构如图2所示。
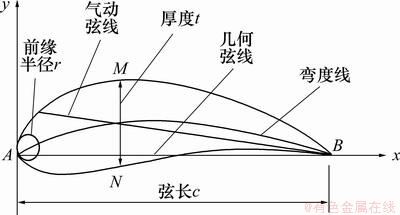
图1 翼型的几何参数
Fig.1 Geometric parameters of aerofoil
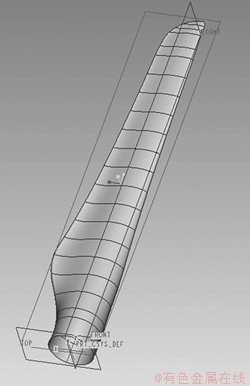
图2 风力桨叶的结构
Fig.2 Structure of blades of MW wind turbine
风轮由桨叶构成,桨叶的结构设计质量直接影响桨叶的性能,从而影响风能的利用效率。叶片的基本气动理论[2]有贝兹理论、Glauert理论、Wilson理论、片条理论和动量-叶素理论。其中,动量-叶素理论是目前运用最广的叶片设计和气动分析方法,该方法还衍生了很多修正方法,它着重考虑和计算了轴向和切向速度干涉因子,由此计算其他参数分量,并用2个干涉因子对气动性能进行计算。
2 兆瓦级风电机组风力桨叶多学科设计优化
2.1 兆瓦级风电机组风力桨叶多学科设计优化思路
多学科设计优化是一种通过充分利用和探索系统中相互作用的协同机制来设计复杂系统和子系统的方法[10-12]。兆瓦级风电机组风力桨叶多学科设计优化理论方法的主要思想是:在复杂系统设计整个过程中集成各个学科的知识,应用有效的设计、优化策略和分布式计算机网络系统对风力桨叶进行设计,通过充分利用各个学科(子系统)之间的相互作用所产生的协同效应,获得风力桨叶的整体最优设计结果。兆瓦级风电机组风力桨叶分级多学科设计优化结构如图3所示。
按兆瓦级风电机组风力桨叶总体级和部件级(风轮总成和桨叶总成)以及零件级(流场、压力场、声场和应力场等)三级进行多学科优化设计。兆瓦级风电机组风力桨叶总体优化设计的功能是使兆瓦级风电机组风力桨叶的设计成本最低、质量最小、耐久性寿命较长,同时,向各部件分配指标,并以总体指标与部件指标一致为约束条件;部件级优化设计以与总体级分配指标相差最小为目标函数,在满足部件级的约束条件下,向所属各零件分配指标;零件级优化设计以与部件级分配指标相差最小为目标函数,通过调整零件几何结构尺寸,使得零件级的各学科约束条件得到满足。通过以上三级优化,使得各零部件与总体间设计达成一致协调(也就是说,各零部件与总体间的复杂耦合关系通过一致性约束解耦),并找到综合最优的设计方案。在以上过程中,若上一级系统包含过多的下一级系统,则可根据需要在2级之间增加1级或多级系统。
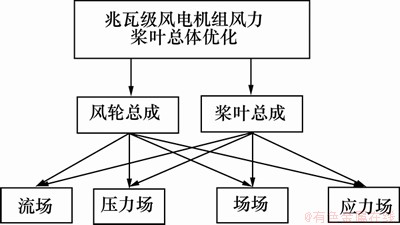
图3 多学科设计优化分级结构
Fig.3 Grading structure of multidisciplinary optimization design
2.2 兆瓦级风电机组风力桨叶多学科设计优化模型
考虑兆瓦级风电机组风力桨叶的气动性能、质量、桨片根部的极限推力、噪声大小等方面的因素,根据MDO设计优化思想,可给出兆瓦级风电机组风力桨叶优化设计的MDO过程示意图,如图4所示。
兆瓦级风电机组风力桨叶多学科设计问题是一个数学规划的优化问题,可描述为
min f(X, Y)s.t. gi(X, Y)≤0; i=1, 2, …, n (1)
式中:f(X, Y)为目标函数,f(X, Y)=W1f1(X, Y)/f10(X, Y)+ W2f2(X, Y)/f20(X, Y)+W3f3(X, Y)/f30(X, Y)+W4f4(X, Y)/ f40(X, Y);f1(X, Y)为气动性能目标函数,f2(X, Y)为质量目标函数;f3(X, Y)为桨片根部的极限推力目标函数;f4(X, Y)为噪声水平目标函数;f10(X, Y)为未多学科优化前的风能利用系数;f20(X, Y)为未多学科优化前的质量;f30(X, Y)为未多学科优化前的兆瓦级风电机组风力桨叶根部的极限推力;f40(X, Y)为未多学科优化前的兆瓦级风电机组风力桨叶噪声;W1,W2,W3和W4分别为气动性能目标函数、质量目标函数、桨片根部的极限推力目标函数和噪声水平目标函数在总体目标规划中的加权系数,且W1+W2+W3+W4=1;X为设计变量,X=(X1, X2, …, Xm, …, XM)T;Y为状态变量,Y=(Y1, Y2, …, Yk, …, YK)T;gi(X,Y)为约束条件。
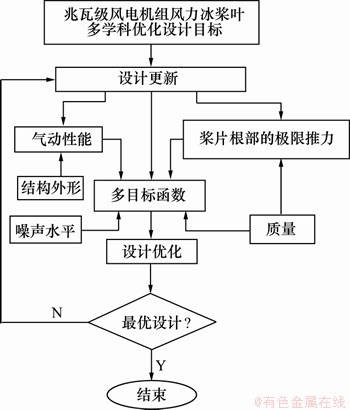
图4 兆瓦级风电机组风力桨叶MDO过程示意图
Fig.4 Chart of MDO process of blades of MW wind turbine
兆瓦级风电机组风力桨叶MDO求解过程示意图如图5 所示,其中:设计变量X表示兆瓦级风电机组风力桨叶的特征,在设计过程中可被设计者控制相互独立的变量;Z为兆瓦级风电机组风力桨叶固定不变参数;状态变量Y为描述兆瓦级风电机组风力桨叶性能和特征的参数,也可表示为Y=[y12, y13, y14, y21, y23, y24, y31, y32, y34, y41, y42, y43],此时Y为所有连接变量组成的向量,且yij(i,j=1, 2, 3, 4;i≠j)为学科之间的耦合变量,或称连接变量,它是子系统i 的输出变量,同时是子系统j 的输入变量。4个学科分析(contributing analysis, CA)之间通过连接变量Y相互交换信息。系统分析可由如下非线性联立方程组表示:
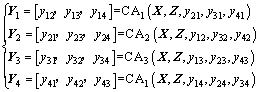 (2)
(2)
最后对兆瓦级风电机组风力桨叶设计进行系统分析(system analysis, SA),从而得到优化设计结果。
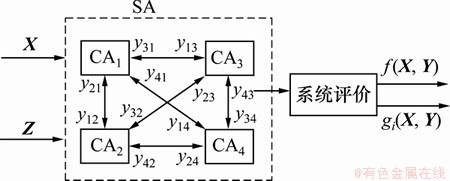
图5 兆瓦级风电机组风力桨叶MDO 求解过程示意图
Fig.5 Chart of resolution process about MDO of blades of MW wind turbine
2.3 自适应混沌优化算法
给定权值W1,W2,W3和W4的取值范围,利用自适应变尺度混沌优化算法[13-14]对式(1)所示的全局优化问题求解,权值W1,W2,W3和W4对应全局优化问题的最小值。选择式(3)所示的折叠次数无限一维自映射作为产生搜索迭代用的混沌变量的混沌模型,用K1和K2分别表示粗、细迭代次数。
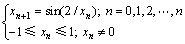 (3)
(3)
混沌优化算法的基本步骤如下。
(1) 算法初始化。置K1=1,K2=1,并给定2个较大的正整数N1 和N2,用随机数产生x0,代入式(3),产生i个混沌变量xi,n+1(i=1, …, M)作为产生搜索迭代用的混沌变量。
(2) 混沌变量在设计变量区间上的粗略转化。利用式(4)将以上产生的第i个混沌变量由取值范围[-1, 1]变换到优化设计变量区间[ai, bi]上的混沌变量。
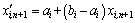 (4)
(4)
(3) 用混沌变量进行粗迭代搜索。令xi(K1)=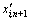 ,计算优化解fi(K1),令
,计算优化解fi(K1),令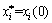 ,
,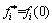 。
。
1) 若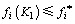 ,则
,则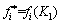 ,
,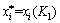 ;
;
2) 若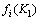 >
>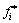 ,则放弃xi(K1)。当K1≤N1时,进入下一次迭代,K1:=K1+1;当K1>N1 时,结束粗迭代。
,则放弃xi(K1)。当K1≤N1时,进入下一次迭代,K1:=K1+1;当K1>N1 时,结束粗迭代。
(4) 混沌变量搜索区间的缩小。设
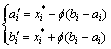 (5)
(5)
式中: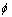 为收缩因子,
为收缩因子,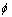 ∈(0, 0.5)。为了保证新范围不至于越界,进行如下处理:若
∈(0, 0.5)。为了保证新范围不至于越界,进行如下处理:若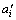 <ai,则
<ai,则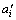 = ai;若
= ai;若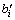 >bi,则
>bi,则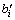 =bi 。因此,
=bi 。因此,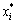 在新区间[
在新区间[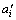 ,
, 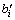 ]上进行还原处理后
]上进行还原处理后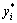 由式(6)确定:
由式(6)确定:
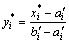 (6)
(6)
(5) 混沌变量在设计变量区间上的细转化。
若经过第3步的若干搜索,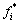 都保持不变,则利用式(7)将
都保持不变,则利用式(7)将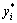 与
与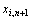 的线性组合作为新的混沌变量,用此混沌变量进行搜索。
的线性组合作为新的混沌变量,用此混沌变量进行搜索。
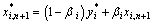 (7)
(7)
式中:βi为自适应调节系数,0<βi<1。自适应调节系数βi采用如下方法进行自适应确定:
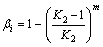 (8)
(8)
式中:m为整数,根据优化目标函数而定,本文中取m=2。
在细迭代搜索初期,由于(x1, x2, …, xn)变动较大,故需要选用较大的βi;随着搜索的进行,逐渐接近最优点,故需要选用较小的βi,以便于在(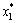 ,
, 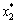 , …,
, …, 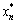 )所在的较小范围内进行搜索。
)所在的较小范围内进行搜索。
(6) 用混沌变量进行细迭代搜索。令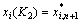 ,计算优化解
,计算优化解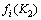 。
。
1) 若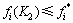 ,则
,则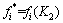 ,
,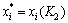 ;
;
2) 若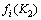 >
>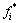 ,则放弃
,则放弃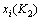 。当K2≤N2时,进入下一次迭代,K2:=K2+1;当K2>N2时,结束细迭代。
。当K2≤N2时,进入下一次迭代,K2:=K2+1;当K2>N2时,结束细迭代。
当得到最优解W1,W2,W3和W4后,将所求得的最优解W1,W2,W3和W4存入内存。
3 兆瓦级风电机组风力桨叶多目标函数的建立与求解
风力桨叶气动性能对整机性能的影响极大,因此,选择合适的气动外形便成为设计的主要任务之一;另外,桨叶的质量、载荷和噪声性能也是很重要的设计目标:所以,选取这4个与气动和结构设计相关的设计目标, 即气动性能最好、桨叶的质量最小、桨叶根部的极限推力载荷最小和噪声最小。
假设桨叶被分成n个截面,优化变量由每个截面上的弦长、扭角和翼型厚度组成。弦长为cl,c2,…,cn;扭角为β1,β2,…,βn;翼型厚度为t1,t2,…,tn。
3.1 兆瓦级风电机组风力桨叶多目标函数设计
3.1.1 气动性能目标函数
对于定桨距风电机组,衡量其性能的基本要素是风电机组的年能量输出。而对于变桨距风电机组,一般当风电机组输出功率超过额定功率时,通过改变桨距角使输出功率等于额定功率,为此,采用给定风电机组风轮直径和转速,且叶尖桨距角为0°、风速为设计风速时的风能利用系数作为气动性能的设计目 标[12],其优化变量为(X1,Y1)。其中:X1包括各截面的弦长ci、扭角βi和翼型厚度ti;Y1为截面到根部的距离di。
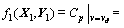
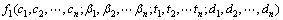 (9)
(9)
式中:ci (i=1, 2, …, n)为第i个截面的弦长;βi (i=1, 2, …, n)为第i个截面的扭角;ti (i=1, 2, …, n)为第i个截面的翼型厚度;di (i=1, 2, …, n)为第i个截面到根部的距离。
桨叶的气动性能评估方法采用了修正的动量叶素理论。基于经典的动量-叶素理论并结合各种修正参量建立风力桨叶气动性能计算的理论模型,考虑叶尖和轮毂损失,引入叶尖和轮毂修正因子及湍流时计算诱导修正因子,建立计算模型。
3.1.2 质量目标函数
为得到叶片截面的质量分布和叶片的总质量,以主复合层的厚度和位置、尾缘加强层的厚度和位置为变量,计算采用薄壁梁自由弯曲时的正应力方程[15]:
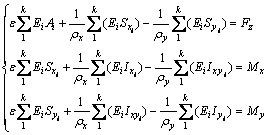 (10)
(10)
式中:k为截面单元个数;ε为应变;Ei 为弹性模量;Sxi和Syi分别为截面翼型上第i个单元在x和y方向的静力矩;Ixyi,Ixi和Iyi为第i个单元绕xy平面、x轴、y轴的惯性矩;ρx和ρy为截面曲率半径;截面上任意1点i处的应力σi为
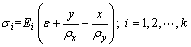 (11)
(11)
再结合给定的安全系数和单目标优化算法,可以得到叶片关键截面的主复合层厚度和位置以及尾缘加强层的厚度和位置,积分后可得到截面的线质量Mj。再将所有截面的线质量积分,就可以得到叶片的总质量。目标可以表示如下:
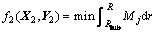 (12)
(12)
式中:Rhub为轮毂的半径;R为风轮半径。优化变量为(X2, Y2)。X2包括的设计变量参数与X1 的相同,Y2 不包括任何状态变量参数。
3.1.3 桨叶根部的极限推力载荷目标函数
对于整个桨叶,从叶根到叶尖的展向上,最大的载荷在叶根处,通过对主导叶片结构设计的挥舞方向弯矩和轮毂中心载荷进行分析,本文对桨叶极限载荷的计算采用一种简化的载荷工况和给定的安全系数的方法。此设计目标可以表述为
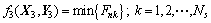 (13)
(13)
式中:Fnk为各个运行状态的极限推力载荷,其由修正的动量叶素理论计算得到;Ns为选取的计算状态数。优化变量为(X2, Y2),其中X3包括的设计变量参数与X1的相同,Y3包括截面到根部的距离di、截面处的应力σi、压力pi和应变εi。
3.1.4 噪声水平目标函数
桨叶与稳态来流相互作用形成边界层与尾流,由此造成的气流波动产生的噪声称为翼型自身噪声,是空气动力本身造成的,即使在稳态、无湍流扰动的情况下也会产生,包括湍流边界层尾缘噪声、层流边界层脱落涡噪声、分离流噪声、钝尾缘噪声和叶尖涡噪声[16]。叶尖涡噪声是由于叶尖的绕流而产生,与其他噪声相比较小,而且只出现在整个叶片的叶尖处,对翼型设计本身影响不大;同时,大多数风电机组工作在湍流条件下:所以,对叶尖涡噪声和层流边界层脱落涡噪声不进行计算。
在高雷诺数下,湍流边界层尾缘噪声对总体噪声水平贡献较大,是风力机高频噪声的主要来源。吸力面和压力面均产生此类噪声,可表示为:
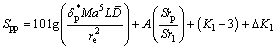 (14)
(14)
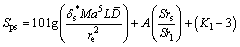 (15)
(15)
式中:Spp和Sps分别为压力面和吸力面湍流边界层尾缘噪声;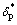 和
和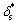 分别为压力面和吸力面尾缘边界层位移厚度;Ma,L,re和
分别为压力面和吸力面尾缘边界层位移厚度;Ma,L,re和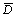 分别为马赫数、展向长度、测试距离和指向性函数;Srp,Srs和Sr1分别为压力面和吸力面基于边界层位移厚度的斯特劳哈尔数、经验斯特劳哈尔数;A为谱形状函数;K1和ΔK1为修正因子的经验常数。
分别为马赫数、展向长度、测试距离和指向性函数;Srp,Srs和Sr1分别为压力面和吸力面基于边界层位移厚度的斯特劳哈尔数、经验斯特劳哈尔数;A为谱形状函数;K1和ΔK1为修正因子的经验常数。
定义相应斯特劳哈尔数为
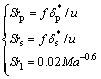 (16)
(16)
式中:f 为噪声频率;u为来流风速。
定义指向性函数为
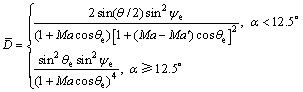 (17)
(17)
式中:θe为极指向角;ψe为位指向角;Ma′为对流马赫数(Ma′≈0.8Ma );а为攻角。
随着攻角的增加,吸力面边界层湍流加剧,形成不稳定气流,在一定条件下会脱离边界层形成分离流,由此而产生的噪声称为分离流噪声,其经验公式类似于湍流边界层噪声,记为:
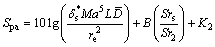 (18)
(18)
式中:SPα 为分离流噪声;Sr2,K2和B分别为经验斯特劳哈尔数、修正因子经验常数和谱形状函数。
定义相应斯特劳哈尔数为
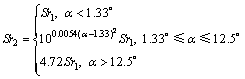 (19)
(19)
钝尾缘噪声是钝尾缘引起的脱落涡所产生,噪声频率和幅度在很大程度上取决于翼型钝尾缘的几何尺寸。当尾缘厚度远大于边界层厚度时,此类噪声对翼型自身总体噪声水平影响较大,可通过锐化边缘来消除。噪声水平可记为
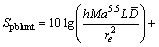
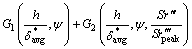 (20)
(20)
式中:Spblunt为钝尾缘噪声;h和ψ分别为钝尾缘厚度和尾缘角;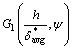 和
和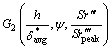 为经验函数;
为经验函数;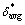 为尾缘处压力边界层位移厚度和吸力边界层位移厚度的平均值;Sr′′′为基于尾缘厚度的斯特劳哈尔数;
为尾缘处压力边界层位移厚度和吸力边界层位移厚度的平均值;Sr′′′为基于尾缘厚度的斯特劳哈尔数;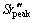 斯特劳哈尔数峰值。
斯特劳哈尔数峰值。
定义相应斯特劳哈尔数为:
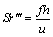 (21)
(21)
以上对桨叶翼型自身各类噪声进行了描述和计算,而对于工作中翼型,这几类噪声源往往是同时存在的,需要对这几类噪声的声压级进行叠加,所得总体噪声水平公式如下:
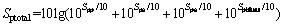 (22)
(22)
所以,令噪声水平目标函数为:
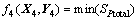 (23)
(23)
式中:优化变量为(X4,Y4);X4=X1;Y4=Y1。
3.1.5 约束条件
对于优化设计变量,采用以下约束:
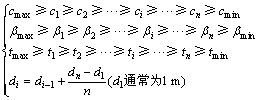 (24)
(24)
式中:cmin和cmax分别为优化设计截面翼型的最小弦长和最大弦长;βmin和βmax分别为优化设计截面翼型的最小扭角和最大扭角;tmin和tmax分别为优化设计截面翼型的最小厚度和最大厚度。
以某兆瓦级风力机桨叶为优化对象,桨叶的基本设计参数如表1所示。沿桨叶展向取40个截面进行设计优化。在式(24)中,n=40,cmin= 952.21,cmax=3 345.58,βmin=0,βmax=10.6,tmin=11,tmax=30。
3.2 兆瓦级风电机组风力桨叶设计优化仿真流程
兆瓦级风电机组风力桨叶的参数化建模通过自编程序对自定的、统一格式的参数文件进行操作,分别生成符合流场仿真分析、应力场仿真分析、声场仿真分析和压力场仿真分析的几何模型文件,并通过优化平台将不同物理场的仿真分析软件和自编程序进行集成,从而实现兆瓦级风电机组风力桨叶多学科设计优化。不同物理场的耦合关系以及优化仿真集成的流程如图6所示。
表1 基本设计参数
Table 1 Basic parameters of design
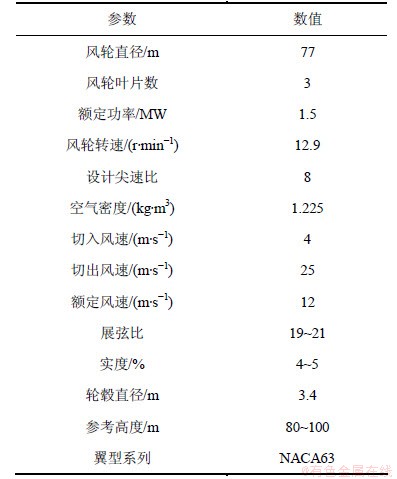
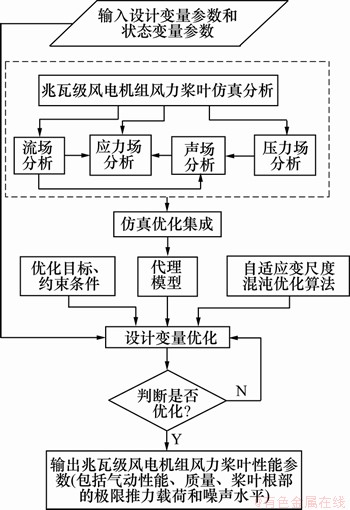
图6 兆瓦级风电机组风力桨叶设计仿真优化流程图
Fig.6 Flow chart of design and optimization of blades of MW wind turbine
3.3 兆瓦级风电机组风力桨叶多学科设计优化结果
兆瓦级风电机组风力桨叶系统级优化的优化算法为自适应混沌优化算法,其优化变量为(X1, Y1)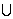 (X2, Y2)
(X2, Y2)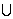 (X3, Y3)
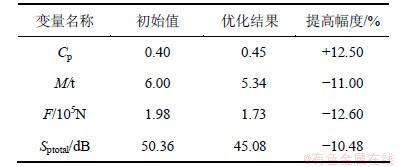
(X3, Y3)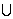 (X4, Y4)。各系统的优化通过VB软件实现双层并行运算。兆瓦级风电机组风力桨叶多学科设计优化前后优化目标的相关参数值如表2所示。从表2可以看出:兆瓦级风电机组风力桨叶风能利用系数Cp增加12.5%,质量M 减少11%,桨叶根部的极限推力载荷F减少12.6%,噪声Sptotal减小10.48%。
(X4, Y4)。各系统的优化通过VB软件实现双层并行运算。兆瓦级风电机组风力桨叶多学科设计优化前后优化目标的相关参数值如表2所示。从表2可以看出:兆瓦级风电机组风力桨叶风能利用系数Cp增加12.5%,质量M 减少11%,桨叶根部的极限推力载荷F减少12.6%,噪声Sptotal减小10.48%。
表2 MDO优化目标的相关参数值
Table 2 Values of correlative MDO objective parameters
3.4 兆瓦级风电机组风力桨叶多学科设计优化性能对比
为比较优化前后风力桨叶性能,通过多学科设计优化得到优化前后风力桨叶的升力系数和气动性能的对比曲线,分别如图7和图8所示。
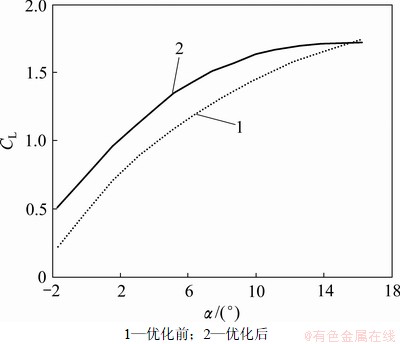
图7 升力系数对比
Fig.7 Lift coefficient comparisons
从图7可以看出:在大部分攻角范围内,优化后的升力系数比优化前的升力系数要大。从图8可以看出:在尖速比小于额定尖速比的情况下,经多学科设计优化后,风力桨叶的功率利用系数明显得到较大幅度提高,即风能利用系数比优化前的高。
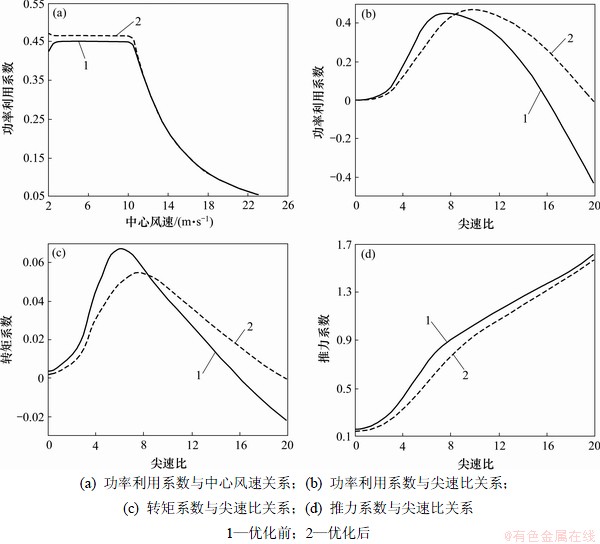
图8 气动性能对比
Fig.8 Comparisons of aerodynamic performance
4 结论
(1) 兆瓦级风电机组风力桨叶风能利用系数Cp增加12.5%,质量M 减少11%,桨叶根部的极限推力载荷F减少12.6%,噪声Sptotal减小10.48%。兆瓦级风电机组风力桨叶翼型的升力系数和气动性能得到了较大的优化。
(2) 采用多学科设计优化方法来进行兆瓦级风电机组风力桨叶的设计,通过充分考虑各学科之间的耦合效应,既提高了兆瓦级风电机组风力桨叶的气动性能,又降低了设计成本,减小了质量,因而为兆瓦级风电机组风力桨叶设计提供了一种新的思路。
参考文献:
[1] Sanchez I. Adaptive combination of forecasts with application to wind energy[J]. International Journal of Forecasting, 2008, 24(4): 679-693.
[2] Ammara I, Leclerc C, Masson C. A viscous three-dimensional differential/actuator-disk method for the aerodynamic analysis of wind farms[J]. Journal of Solar Energy Engineering, 2002, 124(11): 345-356.
[3] Fuglsang P, Bak C. Development of the rRisφ wind turbine airfoils[J]. Wind Energy, 2004, 7(2): 145-162.
[4] Wood D H. Dual purpose design of small wind turbine blades[J]. Wind Engineering, 2004, 28(5): 511-528.
[5] Ronold O, Christensen C J. Optimization of a design code for wind-turbine rotor blades in fatigue[J]. Engineering Structures, 2001, 23: 993-1004.
[6] Kong C, Bang J, Sugiyama Y. Structural investigation of composite wind turbine blade considering various load cases and fatigue life[J]. Energy, 2005, 30: 2101-2114.
[7] Fuglsang P, Bak C, Schcpers J G. Site-specific design optimization of wind turbines[J]. Wind Energy, 2002, 5(6): 261-279.
[8] 王宏亮, 席光. 多目标优化设计方法在翼型气动优化中的应用研究[J]. 工程热物理学报, 2008, 29(7): 1129-1132.
WANG Hongliang, XI Guang. Investigation of multi-objective optimization method on airfoil design[J]. Journal of Engineering Thermophysics, 2008, 29(7): 1129-1132.
[9] 王一伟, 钟星立, 杜特专. 翼型多目标气动优化设计方法[J]. 计算力学学报, 2007, 24(1): 98-102.
WANG Yiwei, ZHONG Xingli, DU Tezhuan. Multi-objective optimization of airfoils[J]. Chinese Journal of Computational Mechanics, 2007, 24(1): 98-102.
[10] 鄂加强, 李志鹏, 袁丁, 等. 新型双向硬密封旋球阀多学科设计优化[J]. 中南大学学报: 自然科学版, 2010, 41(2): 553-560.
E Jiaqiang, LI Zhipeng, YUAN Ding, et al. Multidisciplinary optimization design on new type rotating ball valve with double direction metal sealing[J]. Journal of Central South University: Science and Technology, 2010, 41(2): 553-560.
[11] 谢常清, 鄂加强, 彭雨, 等. 制动电阻器多学科设计优化[J]. 铁道学报, 2008, 30(5): 119-124.
XIE Changqing, E Jiaqiang, PENG Yu, et al. Multidisciplinary design optimization of electric braking resistor[J]. Journal of the China Railway Society, 2008, 30(5): 119-124.
[12] 袁文华, 鄂加强, 龚金科, 等. 自适应粒子群优化的高压共轨燃油喷嘴多学科优化设计[J]. 内燃机工程, 2009(5): 63-67.
YUAN Wenhua, E Jiajiang, GONG Jinke, et al. Multidisciplinary design optimization for fuel nozzle of high pressure common-rail injection system based on self-adaptive particle swarm optimization algorithm[J]. Chinese Internal Combustion Engine Engineering, 2009(5): 63-67.
[13] 鄂加强. 铜精炼过程优化建模与智能控制[M]. 长沙: 湖南大学出版社, 2006: 45-60.
E Jiaqiang. Optimization modeling and intelligent control in copper refining process[M]. Changsha: Hunan University Press, 2006: 45-60.
[14] E Jia-qiang, WANG Chun-hua, WANG Yao-nan, et al. A new adaptive mutative scale chaos optimization algorithm and its application[J]. Control Theory & Applications, 2008, 6(2): 141-145.
[15] 王珑, 王同光, 吴江海, 等. 基于改进NSGA-Ⅱ算法的风力机叶片多目标优化设计[J]. 南京航空航天大学学报, 2011, 43(5): 672-676.
WANG Long, WANG Tongguang, WU Jianghai, et al. Multi-objective optimization design of wind turbine blades based on improved NSGA-Ⅱ[J]. Journal of Nanjing University of Aeronautics & Astronautics, 2011, 43(5): 672-676.
[16] 刘雄, 罗文博, 陈严, 等. 风力机翼型气动噪声优化设计研究[J]. 机械工程学报, 2011, 47(14): 134-139.
LIU Xiong, LUO Wenbo, CHEN Yan, et al. Research on the aerodynamic noise optimization of wind turbine airfoil[J]. Chinese Journal of Mechanical Engineering, 2011, 47(14): 134-139.
(编辑 陈灿华)
收稿日期:2012-01-13;修回日期:2012-03-18
基金项目:湖南省重点实验室开放基金资助项目(2011KFJJ001)
通信作者:鄂加强(1972-),男,湖南湘潭人,博士,副教授,博士生导师,从事热动力设备及过程检测、优化和智能控制研究;电话:0731-88821750;E-mail: ejiaqiang@126.com