文章编号：1004-0609(2012)04-1063-05
Hastelloy C-276合金应力松弛试验及蠕变本构方程
朱 智，张立文，顾森东
(大连理工大学 材料科学与工程学院，大连 116023)
摘 要：对Hastelloy C-276合金分别在不同的温度(750、800、850和900 ℃)和相应的初始应力(250、250、250和200 MPa)条件下进行了多组应力松弛试验。利用试验测得的应力松弛曲线推导出应力松弛过程中蠕变应变速率与应力之间的关系，建立用于描述Hastelloy C-276合金应力松弛行为的蠕变本构方程，通过对蠕变应变速率—应力曲线进行拟合，得到各温度下蠕变本构方程中的材料常数。将蠕变本构方程带入有限元软件MSC.Marc对Hastelloy C-276合金的应力松弛过程进行模拟，模拟得到的应力松弛曲线与试验测得的应力松弛曲线符合得很好，验证蠕变本构方程的可靠性。
关键词：Hastelloy C-276合金；应力松弛试验；蠕变本构方程；真空热胀形
中图分类号：TG146.1+5 文献标志码：A
Stress relaxation test of Hastelloy C-276 alloy and its creep constitutive equation
ZHU Zhi, ZHANG Li-wen, GU Sen-dong
(School of Materials Science and Engineering, Dalian University of Technology, Dalian 116023, China)
Abstract: The stress relaxation tests of Hastelloy C-276 alloy were conducted at different temperatures (750, 800, 850 and 900 ℃) and corresponding initial stress levels (250, 250, 250 and 200 MPa), respectively. Based on the experimental stress relaxation curves, the relationship between creep strain rate and stress was derived. Then, a set of creep constitutive equations were built for Hastelloy C-276 alloy and the material constants of these equations were determined by fitting the creep strain rate-stress curves. The creep constitutive equations were used to simulate the stress relaxation process of Hastelloy C-276 alloy by integrating these equations into finite element software MSC.Marc. The simulated stress relaxation curves agree well with the experimental ones, which verify the reliability of the creep constitutive equations.
Key words: Hastelloy C-276 alloy; stress relaxation test; creep constitutive equation; vacuum hot bulge forming
Hastelloy C-276合金是一种镍基高温合金，具有优良的耐腐蚀性能和高温力学性能，在化工、航空和核电等领域得到了广泛应用[1-2]。在核电领域，Hastelloy C-276合金被用于制造AP1000核主泵的转子屏蔽套。
转子屏蔽套是AP1000核主泵中的关键部件，它可以有效防止转子部件与泵内的冷却剂接触，避免转子部件受到冷却剂的侵蚀[3]。转子屏蔽套是Hastelloy C-276合金板材经剪切、焊接、胀形和矫形工艺制造而成。AP1000核主泵转子屏蔽套的直径尺寸偏差为±0.076 mm[3]，对各工艺的加工精度要求非常高，采用精密剪切和精密焊接工艺也难以达到要求的尺寸精度和圆整度，且其内部留有很大的残余应力，因此，需要对转子屏蔽套进行胀形和矫形，以及必要的去应力退火。真空热胀形是针对薄壁筒形零件开发的成形工艺，它是利用工件与模具间热膨胀系数的差异，在室温下模具可以自由放入工件中，然后放入真空热处 理炉中加热，随着温度的升高，模具与工件发生接触，对工件产生热膨胀力，根据高温软化和应力松弛原理，使工件发生永久的塑性变形和蠕变变形，进而达到成形的目的[4-5]。采用真空热胀形方法对经过精密剪切和精密焊接的转子屏蔽套进行胀形和矫形，不但可以使转子屏蔽套达到尺寸精度和圆整度要求，而且转子屏蔽套内部的残余应力也可以得到很大程度的消除。
真空热胀形的本质是蠕变成形，在利用有限元方法研究转子屏蔽套的真空热胀形过程时，需要建立能用来描述材料应力松弛行为的蠕变本构方程。近些年来，国内外学者针对铝合金和钛合金零件的蠕变成形做了大量的研究。KOWALEWSKI等[6]基于双曲正弦函数，提出了能够描述整个蠕变过程的蠕变损伤统一本构方程，该方程可以预测时效成形过程中铝合金零件内部的应力分布和成形后的最终形状。HO等[7-10]基于蠕变、应力松弛理论和时效动力学，提出一套将传统应力应变分析与微观组织演化，如沉淀相析出、晶粒长大、位错等相结合的统一的蠕变时效本构方程，且基于此本构方程结合有限元软件ABAQUS对7010铝合金壁板的时效成形过程进行了有限元分析。王明伟等[11-14]建立了一系列有限元模型来模拟BT20钛合金筒形零件的真空热胀形过程。LI等[15]和李超等[16]通过对7B04铝合金时效成形中材料微观组织和性能变化的研究，并基于统一理论、长大动力学以及析出强化理论，提出了一个全新概念的等温蠕变时效本构模型。
本文作者针对Hastelloy C-276合金，分别在不同的温度和相应的初始应力条件下进行多组应力松弛试验，并在此基础上，对试验数据进行分析处理，建立能直接用于有限元数值模拟的蠕变本构方程。
1 应力松弛试验
试验材料为Hastelloy C-276合金的热轧棒材，合金的主要成分如表1所列，热处理制度为在1 170 ℃下，固溶0.3 h，然后水冷，内部组织为单相奥氏体。应力松弛试验采用国家标准GB/T 10120—1996规定的拉伸应力松弛试验方法，试验温度为750、800、850和900 ℃，相应的初始应力分别为250、250、250和200 MPa。
图1所示为试验测得的Hastelloy C-276合金应力松弛曲线。由图1可以看出，不同试验温度下，Hastelloy C-276合金的应力松弛行为具有相同的特点，即整个应力松弛过程可以分为两个阶段，第一阶段，试样内部应力松弛得很快，并随着时间的延长逐渐减慢；第二阶段，应力的松弛进一步减慢，随着时间的延长无限趋近于某一应力值，即应力松弛极限。
表1 Hastelloy C-276合金的化学成分
Table 1 Composition of Hastelloy C-276 alloy (mass fraction, %)
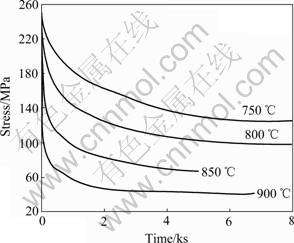
图1 不同温度下Hastelloy C-276合金的应力松弛曲线
Fig. 1 Stress relaxation curves of Hastelloy C-276 alloy at different temperatures
2 蠕变本构方程的建立
蠕变应变速率是材料应力松弛过程中的一个非常重要的物理量，它与应力的关系是材料应力松弛中的最基本的关系式，是利用有限元软件模拟材料蠕变成形过程的基础。
在整个应力松弛过程中，存在如下关系：
(1)
式中：
为总应变；
为弹性应变；
为蠕变应变。应力松弛过程中，总应变保持不变，弹性应变逐渐转化为蠕变应变，则
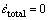(2)
由方程(1)和(2)可以推导出蠕变应变速率与应力的关系：
(3)
式中：
为蠕变应变速率；
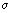为应力；E为材料的弹性模量。
利用方程(3)，由试验测得的应力松弛曲线推导出蠕变应变速率与应力的关系，如图2所示。
用于描述金属材料蠕变行为的本构模型可以分为幂指数函数形式和双曲正弦函数形式两种。在幂指数函数形式的本构模型中，蠕变应变速率与应力的关系如下：
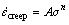(4)
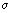式中：为蠕变应变速率；为应力；n为应力指数；A为与材料特性和温度有关的常数。幂指数型本构模型具有形式简单、待定材料常数少等优点，作为一种简单易用的模型得到了广泛应用，但是这种模型只能应用于低应力下的蠕变过程，对于应力较高且发生应力变化的过程，这种模型并不适用。
双曲正弦型蠕变本构模型的典型函数形式为
(5)
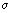式中：为蠕变应变速率；为应力；A、B和n为材料常数。双曲正弦型本构模型能够很好地描述高应力状态下的材料蠕变行为，而且在低应力状态下自然退化为幂指数型本构模型。
从图2可以看出，不同温度下，蠕变应变速率与应力的关系曲线具有相似的特点，即每条曲线都可以分为3个区域，高应力区域、低应力区域和过渡区域。在高应力区域和低应力区域，蠕变应变速率与应力近似呈线性关系，而在中间的过渡区域，蠕变应变速率与应力的关系则比较复杂。考虑蠕变应变速率与应力的关系曲线的特点，本研究在双曲正弦型蠕变本构模型的基础上，建立蠕变本构方程如下：
(6)
式中：A、B、C、D、E、F、G、H和n为材料常数；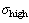
为高应力区域与过渡区域的临界应力；
为低应力区域与过渡区域的临界应力。
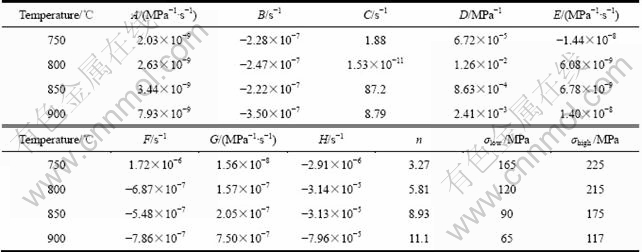
根据建立的蠕变本构方程，利用数据处理软件OriginPro对蠕变应变速率与应力的关系曲线进行拟合，得到蠕变本构方程中的材料常数，如表2所列。
图2 不同温度下Hastelloy C-276合金的蠕变应变速率—应力曲线
Fig. 2 Creep strain rate—stress curves of Hastelloy C-276 alloy at different temperatures: (a) 750 ℃; (b) 800 ℃; (c) 850 ℃; (d) 900 ℃
表2 蠕变本构方程材料常数
Table 2 Material constants of creep constitutive equations
3 蠕变本构方程的验证
利用MSC.Marc有限元软件建立Hastelloy C-276合金试样应力松弛过程的有限元模型，图3所示为模型中应力松弛试样的有限元网格，利用Crplaw子程序进行二次开发，将建立的Hastelloy C-276合金蠕变本构方程带入到有限元模型中。
图3 Hastelloy C-276合金应力松弛过程的有限元模型
Fig. 3 Finite element model of stress relaxation for Hastelloy C-276 alloy
图4所示为模拟结果与试验结果的对比。由图4可以看出，模拟得到的应力松弛曲线与实验测得的应力松弛曲线符合的很好，说明建立的蠕变本构方程能较好的描述Hastelloy C-276合金在试验温度和初始应力水平下的应力松弛行为。
图4 不同温度下模拟应力松弛曲线与试验应力松弛曲线的对比
Fig. 4 Comparison between simulated stress relaxation curves and experimental results at different temperatures
4 结论
1) 针对Hastelloy C-276合金分别在不同的温度和相应的初始应力条件下进行多组应力松弛试验，测得一系列应力松弛曲线，并由此推导出应力松弛过程中蠕变应变速率与应力之间的关系。
2) 基于蠕变应变速率与应力的关系曲线，在双曲正弦函数蠕变本构模型的基础上，建立用于描述Hastelloy C-276合金应力松弛行为的蠕变本构方程，通过对蠕变应变速率与应力关系曲线进行拟合，得到各温度下蠕变本构方程中的材料常数。
3) 将蠕变本构方程带入MSC.Marc有限元软件对Hastelloy C-276合金的应力松弛过程进行模拟，模拟得到的应力松弛曲线与试验测得的应力松弛曲线符合得很好，验证了建立的蠕变本构方程。
REFERENCES
[1] AHMAD M, AKHTER J I, AKHTAR M, IQBAL M, AHMED E, CHOUDHRY M A. Microstructure and hardness studies of the electron beam welded zone of Hastelloy C-276[J]. Journal of Alloys and Compounds, 2005, 390(1/2): 88-93.
[2] AKHTER J I, SHAIKH M A, AHMAD M, IQBAL M, SHOAIB K A, AHMAD W. Effect of aging on the hardness and impact properties of Hastelloy C-276[J]. Journal of Materials Science Letters, 2001, 20(4): 333-335.
[3] 关 锐, 高永军. AP1000反应堆主泵屏蔽套制造工艺浅析[J]. 中国核电, 2008, 1(1): 49-53.
GUAN Rui, GAO Yong-jun. Brief analysis on fabrication process of AP1000 reactor coolant pump can[J]. China Nuclear Power, 2008, 1(1): 49-53.
[4] IDEM K, PEDDIESON J. Simulation of the age forming process[J]. Journal of Manufacturing Science and Engineering, 2005, 127(2): 165-172.
[5] WANG M W, ZHANG L W, PEI J B, LI C H, ZHANG F Y. Effect of temperature on vacuum hot bulge forming of BT20 titanium alloy cylindrical workpiece[J]. Transactions of Nonferrous Metals Society of China, 2007, 17: 957-962.
[6] KOWALEWSKI Z L, HAYHURST D R, DYSON B F. Mechanisms-based creep constitutive equations for an aluminum alloy[J]. Journal of Strain Analysis, 1994, 29(4): 309-316.
[7] HO K C, LIN J, DEAN T A. Modeling of springback in creep forming thick aluminum sheets[J]. International Journal of Plasticity, 2004, 20(4/5): 733-751.
[8] HO K C, LIN J, DEAN T A. Constitutive modeling of primary creep for age forming an aluminum alloy[J]. Journal of Materials Processing Technology, 2004, 153/154: 122-127.
[9] JEUNECHAMPS P P, HO K C, LIN J, PONTHOT J P, DEAN T A. A closed form technique to predict springback in creep age- forming[J]. International Journal of Mechanical Sciences, 2006, 48: 621-629.
[10] LIN J, HO K C, DEAN T A. An integrated process for modeling of precipitation hardening and springback in creep age- forming[J]. International Journal of Machine Tools & Manufacture, 2006, 46: 1266-1270.
[11] 王明伟, 张立文, 原思宇, 戚 琳, 张凡云, 李辰辉. BT20钛合金筒形件真空热胀形过程热力耦合有限元分析[J]. 塑性工程学报, 2007, 14(2): 109-113.
WANG Ming-wei, ZHANG Li-wen, YUAN Si-yu, QI Lin, ZHANG Fan-yun, LI Chen-hui. Coupled thermo-mechanical FEM analysis of the vacuum hot bulge forming of BT20 Titanium alloy cylindrical workpiece[J]. Journal of Plasticity Engineering, 2007, 14(2): 109-113.
[12] 王明伟, 张立文, 裴继斌, 李辰辉, 张凡云. 钛合金筒形件真空热胀形过程数值模拟及模型优化[J]. 材料热处理学报, 2007, 28: 363-366.
WANG Ming-wei, ZHANG Li-wen, PEI Ji-bin, LI Chen-hui, ZHANG Fan-yun. FE simulation of vacuum hot bulge forming of titanium alloy and model optimization[J]. Transactions of Materials and Heat Treatment, 2007, 28: 363-366.
[13] 王明伟, 张立文, 裴继斌, 戚 琳, 张凡云, 李辰辉. 温度对BT20合金筒形件真空热胀形影响模拟研究[J]. 材料热处理学报, 2007, 28(2): 141-144.
WANG Ming-wei, ZHANG Li-wen, PEI Ji-bin, QI Lin, ZHANG Fan-yun, LI Chen-hui. Simulation and research on influence of temperature on vacuum hot bulge forming of BT20 alloy cylindrical workpiece[J]. Transactions of Materials and Heat Treatment, 2007, 28(2): 141-144.
[14] 王明伟, 张立文, 张凡云, 李辰辉. 钛合金筒形件真空热胀形壁厚效应的数值模拟[J]. 稀有金属材料与工程, 2007, 36(10): 1772-1775.
WANG Ming-wei, ZHANG Li-wen, ZHANG Fan-yun, LI Chen-hui. Numerical simulation of wall thickness effects in vacuum hot bulge forming process of titanium alloy cylindrical workpiece[J]. Rare Metal Materials and Engineering, 2007, 36(10): 1772-1775.
[15] LI C, WAN M, WU X D, LIN H. Constitutive equations in creep of 7B04 aluminum alloys[J]. Materials Science and Engineering A, 2010, 527: 3623-3629.
[16] 李 超, 万 敏, 金 兴, 黄 霖. 7B04铝合金时效成形本构模型研究与有限元应用[J]. 塑性工程学报, 2010, 17(5): 61-65.
LI Chao, WAN Min, JIN Xing, HUANG Lin. A creep forming constitutive model of 7B04 aluminum alloy and its application in FEM[J]. Journal of Plasticity Engineering, 2010, 17(5): 61-65.
(编辑 李艳红)
基金项目：国家重点基础研究发展计划资助项目(2009CB724307)
收稿日期：2011-03-15；修订日期：2011-10-20
通信作者：张立文，教授，博士；电话：0411-84706087；E-mail: commat@mail.dlut.edu.cn
