Trans. Nonferrous Met. Soc. China 28(2018) 1114-1122

Isothermal compression behavior and constitutive modeling of Ti-5Al-5Mo-5V-1Cr-1Fe alloy

Li-li CHANG, Li-wei ZHENG

School of Materials Science and Engineering, Shandong University, Ji’nan 250061, China

Received 12 December 2016; accepted 18 September 2017

Abstract: Hot compression behavior of Ti-5Al-5Mo-5V-1Cr-1Fe alloy with an equiaxed (α+β) starting microstructure was investigated by isothermal compression test and optical microscopy. Based on the true strain-stress data with temperature correction, constitutive models with a high accuracy were developed and processing maps were established. Strain inhomogeneity at different locations in the compressed sample is reduced by raising temperature, leading to a uniform distribution of α phases. For the temperature range of 800-840 °C with a strain rate of 10 s^-1, the transformed volume fraction of α phase increases and the average grain size of α phase decreases slightly with increasing the temperature, indicating co-existence of dynamic recovery and dynamic recrystallization. Flow localization and faint β grain boundaries are observed at the strain rate of 10 s^-1 in the temperature range of 860-900 °C. The processing map analysis shows that hot working of Ti-5Al-5Mo-5V-1Cr-1Fe alloy should be conducted with the strain rate lower than 0.01 s^-1 to extend its workability.

Key words: Ti-5Al-5Mo-5V-1Cr-1Fe alloy; isothermal compression; constitutive equations; processing map

1 Introduction

Titanium alloys are widely used in aerospace, aviation industries due to their high specific strength and excellent corrosion resistance. Ti-5Al-5Mo-5V-1Cr- 1Fe alloy is a near β-type titanium alloy with high strength, high ductility and deep hardenability, which has been widely used as a structural component in aircraft [1]. However, the microstructure of titanium alloys is very sensitive to processing parameters, such as strain rate, deformation degree and deformation temperatures during hot working process [2-5]. Ti-5Al-5Mo-5V-1Cr-1Fe alloy has a narrow processing window due to its high flow stress. Thus, it is very crucial to investigate the deformation behavior during hot deformation process in order to extend the workability. LUO et al [1] investigated the correlation between the flow behavior and the microstructure evolution during hot working of TC18 (Ti-5Al-5Mo-5V-1Cr-1Fe) alloy. It was shown that the shapes of flow curves were dependent on the competing processes of the work hardening, the thermal softening and the microstructure-related softening [6,7]. NING et al [8] studied the competition between dynamic recovery (DRV) and dynamic recrystallization (DRX) during hot deformation for TC18 titanium and found that various work hardening behaviors corresponded to different dynamic softening mechanisms. QU et al [9] studied the hot deformation behavior of Ti-5Al-5Mo- 5V-1Cr-1Fe alloy and confirmed two soften mechanisms of DRV and DRX in Ti-5Al-5Mo-5V- 1Cr-1Fe alloy [9]. LIANG et al [10] constructed power dissipation efficiency distribution map from strain rate sensitivity coefficients for hot deformation of TC18 alloy. LIU et al [2] investigated the effect of the processing parameters on the flow stress of Ti-5Al-5Mo-5V- 1Cr-1Fe alloy and calculated the apparent activation energy for deformation at different deformation conditions. During past years, a substantial amount of effort has been made to describe the flow stress as a function of deformation temperature, strain rate and strain in titanium alloys [11-13]. However, reports on construction of constitutive equations of titanium are all based on the true flow stress-strain curves without any correction ignoring the effect of deformation heat. In the present work, hot compression behavior of Ti-5Al-5Mo-5V-1Cr-1Fe alloy with an equiaxed (α+β) starting microstructure is investigated with the help of isothermal compression tests in the temperature range of 800-900 °C at strain rates of 0.0005-10 s^-1 and strain up to 0.8. Based on the true strain-stress data with temperature correction, constitutive models with a high accuracy are developed and processing maps at the stains of 0.2, 0.6 and 0.8 are established.

2 Experimental

The as-received Ti-5Al-5Mo-5V-1Cr-1Fe bar is in hot-forged condition with a diameter of 280.0 mm. The β transus temperature of as-received material was determined to be ~855 °C and the original optical microstructure is shown in Fig. 1(a). The microstructure consists of β matrix and primary α (white color) with an average grain size of ~1.2 μm. The alloy was treated with a two-stage heat treatment process: for stage I, the as-received bar was heated to 830 °C for 2 h followed by furnace cooling to 750 °C with a cooling rate of 160 °C/h. Then, the sample was held at 750 °C for 2 h followed by air cooling. The optical microstructure of Ti-5Al- 5Mo-5V-1Cr-1Fe alloy after heat treatment is shown in Fig. 1(b). After heat treatment, a (α+β) microstructure with equiaxed α grains was obtained. Due to heat treatment, the average grain size and the volume fraction of α phase were increased to be ~4.7 μm and ~42%, respectively.

Fig. 1 Optical microstructures of Ti-5Al-5Mo-5V-1Cr-1Fe alloy

Cylindrical compression samples with a diameter of 10 mm and a height of 15 mm were machined from the as-received Ti-5Al-5Mo-5V-1Cr-1Fe bar. The hot compression was conducted on a Gleeble-3800 thermal simulator at the deformation temperatures of 800, 820, 840, 860, 880 and 900 °C, the strain rates of 0.0005, 0.001, 0.01, 0.1, 1 and 10 s^-1 and the strain of 0.8. Before compression, the sample was heated and held for 2 min at the deformation temperatures to obtain a homogeneous temperature distribution inside the whole sample. After the hot compression, the sample was quenched into water immediately to maintain the deformation microstructure. For optical microstructure observation, the compressed sample was axially sectioned, ground, polished and chemically etched in a solution of 5 mL HF + 10 mL HNO₃ + 85 mL H₂O.

3 Results

3.1 Flow stress-strain curves

During compression of materials, most plastic work transforms into thermal energy, leading to temperature raising in the sample, which is defined as deformation heating effect. Actually, during isothermal compression, although the temperature at the surface of the sample retains constant, local temperature inside the sample raises at different levels owing to heat energy which can not be dissipated promptly. When the temperature and deformation strain are the same, the effect of deformation heating on the flow stress is mainly dependent on the equivalent strain rate. Therefore, it is crucial to make corrections on the flow stress-strain data in order to obtain accurate constitutive equations. LIANG et al [14] reported a method to establish constitutive relationship considering effect of the deformation heating. According to their discussion, temperature rising due to deformation heat is defined to be

ΔT=T_ex-T_th                                             (1)

And the flow stress could be corrected to be

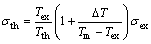                     (2)

where σ_th, σ_ex, T_th, T_ex and T_m are the theoretical stress, experimental stress, theoretical temperature, experimental temperature and melting temperature, respectively. Flow stress-strain curves during isothermal compression of Ti-5Al-5Mo- 5V-1Cr-1Fe alloy with and without temperature correction are shown in Fig. 2. When the strain rate is lower (as shown in Fig. 2(b)), the deformation heat effect is small and its influence on the flow stress is slight. It should be noted that the difference between flow stress-strain curves with and without temperature correction can be neglected when the strain rate is low and the temperature is high enough. For the sample with the same temperature and strain, the deformation heat effect on flow stress becomes significant with increasing the stain rate, as shown in Fig. 2, which can not be ignored anymore. Further investigation indicates that the flow stress with temperature correction is higher than the uncorrected one, indicating that softening occurs due to temperature rising, which is the result of deformation heat. As discussed, making temperature correction with flow stress-strain curves is necessary to acquire accurate constitutive equations for titanium alloys. In the present work, the construction of constitutive equations was based on the flow strain-stress curves after temperature correction to ensure their accuracy.

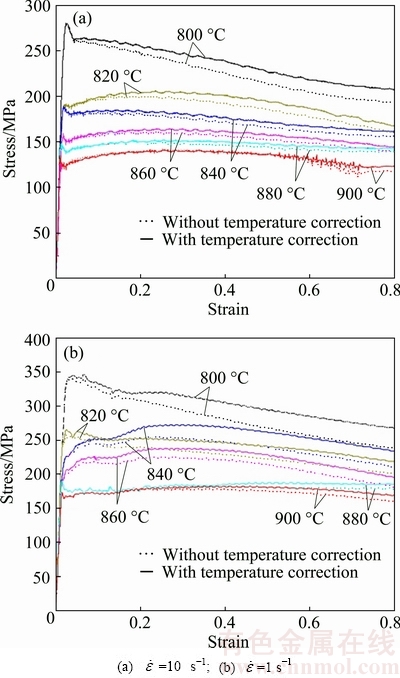
Fig. 2 Comparison between corrected and measured flow stress of Ti-5Al-5Mo-5V-1Cr-1Fe alloy

3.2 Microstructure evolution

Optical microstructures of Ti-5Al-5Mo-5V-1Cr- 1Fe alloys isothermally compressed in temperature range of 800-840 °C with strain rate of 10 s^-1 are shown in Fig. 3. The volume fraction and average grain size were analyzed by Image Pro Plus. For isothermally compressed samples with a strain rate of 10 s^-1 at 800, 820 and 840 °C, the volume fractions of α phase are 41%, 22% and 17%, respectively. Both equiaxed and elongated α grains are observed in Figs. 3(a) and (b), which is a microstructural characteristic of dynamic recovery (DRV) and dynamic recrystallization (DRX), indicating the co-existence of DRV and DRX process during isothermal compression. The long axis of the elongated α grains aligns along the direction with ±45° to the loading direction, which is the direction along the maximum shear stress during compression. During the deformation, accumulated strain inside different β grains is inhomogeneous, resulting in different distortion degrees of α grains. As circled in Fig. 3(a), ellipicity of α grains inside neighbored regions is quite different: α grains inside regions with higher strain are elongated significantly, while those inside regions with lower strain rate exhibit a lower axis ratio. At the boundary zone of regions with elongated α grains, equiaxed α grains are observed. When the deformation temperature is raised to 820 °C, equiaxed and elongated α phases with finer grains are observed to distribute uniformly inside the β matrix. It should be noted that the grain size of α phase is much finer and axis ratio of α grains is much lower, which is considered to be the α-to-β transformation during the heat preservation process before the hot compression. The transformed volume fraction of α phase increases with increasing the temperature, leading to a (α+β) duplex microstructure with a lower volume fraction and fine grains of α phase. Therefore, microstructures with equiaxed and elongated α phase with finer grains and lower axis ratio are observed after isothermal compression. Meanwhile, strain inhomogeneity inside different regions is reduced by raising temperature, leading to a uniform distribution of α phases. When the deformation temperature increases further to 840 °C, the distribution of α phases becomes much more homogeneous and α grains are refined further, as shown in Fig. 3(c). Besides, α grains with necklace structures are observed, which is a typical microstructure characteristic of DRX, indicating that DRX occurs during the isothermal hot compression at 840 °C with a strain rate of 10 s^-1.

Fig. 3 Optical microstructures of Ti-5Al-5Mo-5V-1Cr-1Fe alloy isothermally compressed at different temperatures with strain rate of 10 s^-1

Optical microstructures of isothermally compressed Ti-5Al-5Mo-5V-1Cr-1Fe at higher temperatures with strain rate of 10 s^-1 are shown in Fig. 4. When the hot deformation temperature is close to or higher than the β transus temperature (855 °C), most α phases are transformed into β phase and the retained α phases are elongated to be strings along the direction perpendicular to the compression direction. Typical characteristics of flow localization and faint β grain boundaries are observed in Figs. 4(b) and (c), respectively. As discussed above, the characteristics of isothermal hot compression in (α+β) and β regions are totally different, and therefore, the calculation of constitutive equation for (α+β) and β fields should be conducted separately.

3.3 Constitutive equations

Fig. 4 Optical microstructures of isothermally compressed Ti-5Al-5Mo-5V-1Cr-1Fe alloy at different temperatures with strain rate of 10 s^-1

The constitutive equations relating flow stress to temperature, strain and strain rate were provided by empirical approach. Empirical modeling of the hot deformation of titanium alloys can be expressed by the relationship between flow stress (σ) and strain rate (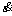) according to the creep power law equation:

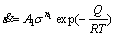                        (3)

where A₁ is a constant, n₁ is the stress component, Q is the activation energy of deformation (kJ/mol), R is the gas constant (8.31 J·mol^-1·K^-1) and T is the deformation temperature (K).

However, this equation is not valid for deformation with high stress levels, due to the fluctuation of n₁ with strain rate. Consequently, the following exponential equation was developed for higher stress:

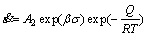                     (4)

where A₂ and β are constants.

However, this relationship is not valid for high temperatures and a strain rate below 1 s^-1. Therefore, a function that includes both Eqs. (3) and (4) was developed:

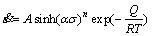                   (5)

where A and α are materials constant and n is the stress component.

The effects of temperature and strain rate on the deformation behavior of materials could be presented by Zener-Holloman parameter (Z) in the exponent type:

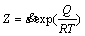                             (6)

By introducing Eq. (6) into Eq. (5), the Zener-Holloman parameter is presented by

Z=A[sinh(ασ)]ⁿ                                 (7)

By introducing Z into Eq. (5), the flow stress can be expressed by Z:

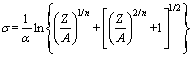             (8)

In the present work, the constitutive equation given in Eq. (5) was used to determine the values for stress component and activation energy for Ti-5Al-5Mo- 5V-1Cr-1Fe alloy. Materials constants were derived by the relationships of ln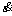-ln σ and ln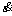-σ at different deformation temperatures. The flow stress at different strain rates are fitted by a group of straight lines. The slopes of the lines present value of n and β, respectively. The value of α is determined to be the ratio of β to n.

According to Eq. (5), there is

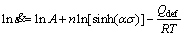              (9)

Differentiating Eq. (9) gives

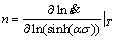                         (10)

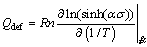                   (11)

By submitting the vales of α, deformation temperature T, strain rate and peak flow stress into   Eq. (11), the relationships of  and 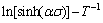 were obtained. The values of n and Q can be derived by the slope of the straight lines of linear regression. The activation energy of deformation can be derived from the Arrhenius plot within a linear range based on the assumption that the phase constituent of the microstructure does not change significantly during the isothermal compression tests [15]. In the case of Ti-5Al-5Mo-5V-1Cr-1Fe alloy, the β transus temperature was determined to be about 855 °C, and the activation energy for (α+β) and β regions was calculated separately. The values of Q_def for temperature range of 800-840 °C and 860-900 °C are determined to be 288.4 and 247.25 kJ/mol, respectively. The average apparent activation energy for deformation of Ti-5Al-5Mo-5V- 1Cr-1Fe alloy at (α+β) region was determined to be 291 kJ/mol by LIU et al [2], which agrees well with the results in this work. For the activation energy in deformation at β region, their results indicated that the Q_def ranged from 214.2 to 150 kJ/mol with an average value of 180 kJ/mol, which is much lower than the value of Q_def (247.25 kJ/mol) in this work. The difference in Q_def in β phase region is considered to be the result of the temperature correction. The relationship between Z and flow stress at a strain of 0.8 is shown in Fig. 5 and parameters from Fig. 5 are summarized in Table 1.

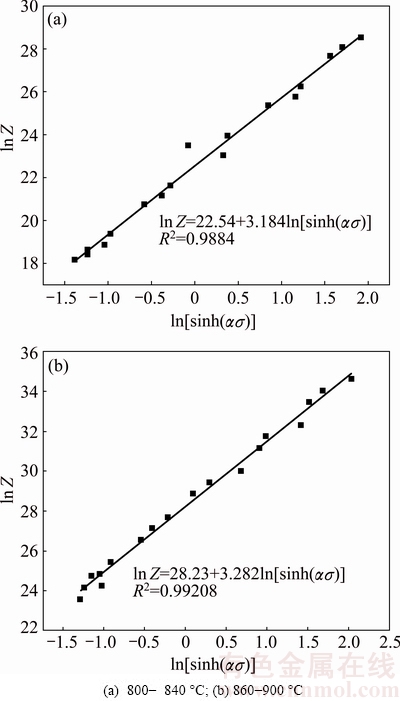
Fig. 5 Relationship between Z and steady flow stress of Ti-5Al-5Mo-5V-1Cr-1Fe alloy at strain of 0.8

Table 1 Parameters in constitutive model from linear fitting of ln Z-ln(sinh(ασ)) of Ti-5Al-5Mo-5V-1Cr-1Fe alloy

Activation energy values for two-phase (α+β) region and β region are different, and therefore, the data are divided into two distinct plots each with a well-defined linear segment, as shown in Figs. 5(a) and (b), respectively. High R² values in Figs. 5(a) and (b) indicate a good approximation of the constitutive model with the experimental data. From the equations for the lines in Fig. 5, the constitutive equations for low and high temperature may be written as

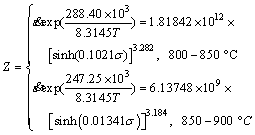   (12)

In order to determine the accuracy of the constitutive relationship, an error analysis has been carried out and the relative errors of measured and calculated steady flow stress are determined. The mean relative error Δ has been calculated by the following form:

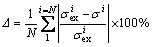                   (13)

where N is the number of experimental data, σ_ex is the measured flow stress and σ is calculated value of flow stress. Results of relative error analysis for temperature ranges are contained in Fig. 6. It is shown that for the two temperature ranges, the relative error is lower than 10% except in some individual cases (880 °C, 0.1 s^-1). Further investigation indicates that the relative error alternatively distributes as positive and negative, which means that the measured flow stress values fluctuate around the calculated ones. The mean relative errors for temperature range of 800-840 and 860-900 °C are determined to be 0.29% and 0.34%, respectively. These small values of relative errors suggest that the established constitutive equations for two temperature ranges are accurate to describe the relationships between the stress, strain rate and temperature.

Fig. 6 Relative error of measured and calculated steady flow stress of Ti-5Al-5Mo-5V-1Cr-1Fe alloy

3.4 Processing map

According to the dynamic materials model (DMM), the instantaneous power P absorbed by the work-piece during hot deformation consists of two parts: dissipater content G and co-content J, in which the former represents power dissipated by plastic deformation and the latter relates to the microstructure evolution. Then, the P can be presented as follows:

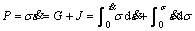            (14)

According to Eq. (14), the power partitioning between J and G is given:

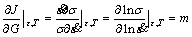            (15)

where m is the exponent of strain rate sensitivity.

Then, the dissipater co-content J can be written as

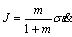                              (16)

The power dissipation efficiency η is defined to be

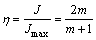                           (17)

At a given strain, the variation of η with strain rate and deformation temperature constitutes the power dissipation map, characterizing the microstructure evolution during hot deformation. Considering the instability during deformation, a continuum criterion predicting the occurrence of plastic flow instability is presented by

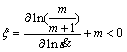                      (18)

where ξ is the instable parameter varying with deformation temperature and strain rate. The values of ξ constitute the instable map and the region with ξ<0 being the plastic flow instability region. A superimposition of the instable map on the power dissipation map constitutes the processing map.

The processing maps obtained at stain of 0.2, 0.6 and 0.8 for Ti-5Al-5Mo-5V-1Cr-1Fe alloy are shown in Fig. 7. The numbers against each contour line represent the efficiency of power dissipation, while dot line represents the boundary of the plastic flow instability region. As shown in Fig. 7, the efficiency of power dissipation at the same temperature decreases with increasing the strain rate. At the same strain rate level, the variation in the efficiency of power dissipation is not significant. The domain with the highest dissipation efficiency of 0.6 appears at the left corner of Fig. 7(a) with the temperature of 800 °C and strain rate of 0.0005 s^-1. Efficiency values as high as 55%-60% indicate superplastic deformation process since the strain rate sensitivities associated with this efficiency range are about 0.4-0.5 [16]. Power dissipation iso-efficiency contours with values lower than 0.39 indicate a transient behavior where unstable microstructure evolution occurs [16]. On the other hand, the critical efficiency for DRX in α-Ti is about 43% [17]. Therefore, the microstructure evolution in the stable region with power dissipation efficiency lower than 0.35 is likely to be caused by DRV, while DRX occurs at the region with η being in the range of 0.35-0.55, as shown in Fig. 3. For processing map obtained at strain of 0.2, there are two domains of instability region and the temperature ranges are 800-823 °C and 885-900 °C, while the corresponding strain rate ranges are 0.3-10 s^-1 and 0.5-10 s^-1, respectively. The two instability domains are located in the (α+β) region and β region, respectively, both being in the higher strain rate region. As the strain increases, the area of instability region increases while the efficiency of power dissipation decreases. When the strain is 0.8, the instability region spreads almost in the whole temperature range (800-900 °C). The occurrence of flow instability is generally related to flow localization, adiabatic shear bands or cracking, as shown in Fig. 4. Therefore, according to the processing map analysis, hot working should be conducted with the strain rate lower than 0.01 s^-1 to avoid defects.

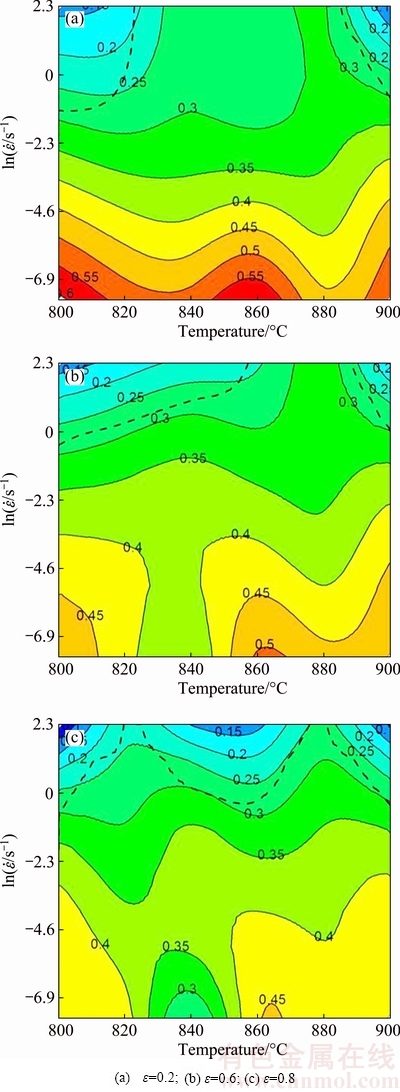
Fig. 7 Processing maps of Ti-5Al-5Mo-5V-1Cr-1Fe alloy isothermally compressed at different strains

4 Conclusions

1) Softening occurs due to temperature rising as a result of deformation heat. Based on flow stress-strain data with temperature correction, the constitutive equations for (α+β) and β region with high accuracy are as follows:

2) Strain inhomogeneity inside different regions is reduced by raising temperature, leading to uniform distribution of α phases. For the temperature range of 800-840 °C (α+β field), the transformed volume fraction of α phase increases and the average grain size of α decreases slightly with increasing the temperature, leading to a (α+β) duplex microstructure with a low volume fraction and fine grains of α phase, which is the result of co-existence of DRV and DRX. When the deformation temperature range is 860-900 °C (β field), flow localization and faint β grain boundaries are observed.

3) The processing maps at different strains indicate that the efficiency of power dissipation at the same temperature decreases with increasing the strain rate. At the same strain rate level, the variation in the efficiency of power dissipation is slight. The domain with the highest dissipation efficiency of 0.6 appears at 800 °C with a strain rate of 0.0005 s^-1, indicating superplastic deformation process. The area of instability region increases with increasing strain and the instability region at strain of 0.8 spreads almost to the whole temperature range (800-900 °C). The processing map analysis shows that hot working of Ti-5Al-5Mo-5V-1Cr-1Fe alloy should be conducted with the strain rate lower than 0.01 s^-1 to avoid deformation defects.

References

[1] LUO J, WANG L F, LIU S F, LI M Q. The correlation between the flow behavior and the microstructure evolution during hot working of TC18 alloy [J]. Materials Science and Engineering A, 2016, 654: 213-220.

[2] LIU S F, LI M Q, LUO J, YANG Z. Deformation behavior in the isothermal compression of Ti-5Al-5Mo-5V-1Cr-1Fe alloy [J]. Materials Science and Engineering A, 2014, 589: 15-22.

[3] SHI X, ZENG W, SHI C, WANG H, JIA Z. The fracture toughness and its prediction model for Ti-5Al-5Mo-5V-1Cr-1Fe titanium alloy with basket-weave microstructure [J]. Journal of Alloys and Compounds, 2015, 632: 748-755.

[4] NIE X A, HU Z, LIU H Q, YI D Q, CHEN T Y, WANG B F, GAO Q, WANG D C. High temperature deformation and creep behavior of Ti-5Al-5Mo-5V-1Fe-1Cr alloy [J]. Materials Science and Engineering A, 2014, 613: 306-316.

[5] SHI X H, ZENG W D, SHI C L, WANG H J, JIA Z Q. Study on the fatigue crack growth rates of Ti-5Al-5Mo-5V-1Cr-1Fe titanium alloy with basket-weave microstructure [J]. Materials Science and Engineering A, 2015, 621: 143-148.

[6] LI K, YANG P. Interaction among deformation, recrystallization and phase transformation of TA2 pure titanium during hot compression [J]. Transactions of Nonferrous Metals Society of China, 2016, 26: 1863-1870.

[7] LU S Q, LI X, WANG K L, DONG X J, FU M W. High temperature deformation behavior and optimization of hot compression process parameters in TC11 titanium alloy with coarse lamellar original microstructure [J]. Transactions of Nonferrous Metals Society of China, 2013, 23: 353-360.

[8] NING Y Q, LUO X, LIANG H Q, GUO H Z, ZHANG J L, TAN K. Competition between dynamic recovery and recrystallization during hot deformation for TC18 titanium alloy [J]. Materials Science and Engineering A, 2015, 635: 77-85.

[9] QU F S, ZHOU Y H, ZHANG L Y, WANG Z H, ZHOU J. Research on hot deformation behavior of Ti-5Al-5Mo-5V-1Cr-1Fe alloy [J]. Materials & Design, 2015, 69: 153-162.

[10] LIANG H Q, NAN Y, NING Y Q, LI H, ZHANG J L, SHI Z F, GUO H Z. Correlation between strain-rate sensitivity and dynamic softening behavior during hot processing [J]. Journal of Alloys and Compounds, 2015, 632: 478-485.

[11] GAO F, LI W, MENG B, WAN M, ZHANG X, HAN X. Rheological law and constitutive model for superplastic deformation of Ti-6Al-4V [J]. Journal of Alloys and Compounds, 2017, 701: 177-185.

[12] VELAY V, MATSUMOTO H, VIDAL V, CHIBA A. Behavior modeling and microstructural evolutions of Ti-6Al-4V alloy under hot forming conditions [J]. International Journal of Mechanical Sciences, 2016, 108: 1-13.

[13] XU X, DONG L M, BA H B, ZHANG Z Q, YANG R. Hot deformation behavior and microstructural evolution of beta C titanium alloy in β phase field [J]. Transactions of Nonferrous Metals Society of China, 2016, 26: 2874-2882.

[14] LIANG H Q, GUO H Z, NING Y Q, YAO Z K, ZHAO Z L. Analysis of the constitutive relationship of TC18 titanium alloy based on the softening mechanism [J]. Acta Metallurgica Sinica: Chinese Edition, 2014, 50: 871-878. (in Chinese)

[15] WANJARA P, JAHAZI M, MONAJATI H, YUE S, IMMARIGEON J P. Hot working behavior of near-α alloy IMI834 [J]. Materials Science and Engineering A, 2005, 396: 50-60.

[16] SESHACHARYULU T, MEDEIROS S C, FRAZIER W G, PRASAD Y V R K. Hot working of commercial Ti-6Al-4V with an equiaxed α-β microstructure: Materials modeling considerations [J]. Materials Science and Engineering A, 2000, 284: 184-194.

[17] PRASAD Y V R K, SASIDHARA S. Hot working guide: A compendium of processing maps [M]. Materials Park: ASM International, 1997.

Ti-5Al-5Mo-5V-1Cr-1Fe等温热压缩行为及本构方程的建立

常丽丽，郑力玮

山东大学 材料科学与工程学院，济南 250061

摘  要：通过等温压缩试验和金相显微镜分析研究具有等轴(α+β)晶粒初始组织的Ti-5Al-5Mo-V-1Cr-1Fe合金的高温压缩性能。基于温度校准的真应力-应变数据，建立了高精度本构模型和加工图。研究结果表明，压缩试样局域应变不均匀性随着温度的升高而减少，使得α相分布均匀。对于温度范围在800~840 °C、应变速率为10 s^-1 的形变条件下，α相的体积分数随温度升高而增加，而α相的平均晶粒尺寸随温度升高而缓慢减小，表明动态回复和动态再结晶同时发生。在温度范围为860~900 °C、应变速率为10 s^-1的变形条件下， 试样中观察到流变局部化和微弱的β相晶界。加工图分析表明，Ti-5Al-5Mo-5V-1Cr-1Fe 合金的热加工适于在应变速率低于0.01 s^-1下进行，以便提高其加工性。

关键词：Ti-5Al-5Mo-5V-1Cr-1Fe合金；等温压缩；本构方程；热加工图

(Edited by Bing YANG)

Foundation item: Project (BS2013CL034) supported by the Promotive Research Fund for Excellent Young and Middle-aged Scientists of Shandong Province, China; Project (51401115) supported by the National Natural Science Foundation of China; Project (GN2013001) supported by Independent Innovation Foundation of Shandong University, China

Corresponding author: Li-li CHANG; Tel: +86-531-88392157; E-mail: lilichang@sdu.edu.cn

DOI: 10.1016/S1003-6326(18)64747-8