J. Cent. South Univ. Technol. (2009) 16: 0474-0477

DOI: 10.1007/s11771-009-0079-2

A novel scale-free network model based on clique growth

WANG Bo(王 波), YANG Xu-hua(杨旭华), WANG Wan-liang(王万良)

(College of Information Engineering, Zhejiang University of Technology, Hangzhou 310032, China)

Abstract: A novel scale-free network model based on clique (complete subgraph of random size) growth and preferential attachment was proposed. The simulations of this model were carried out. And the necessity of two evolving mechanisms of the model was verified. According to the mean-field theory, the degree distribution of this model was analyzed and computed. The degree distribution function of vertices of the generating network P(d) is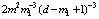, where m and m₁ denote the number of the new adding edges and the vertex number of the cliques respectively, d is the degree of the vertex, while one of cliques P(k) is 2m²k^-3, where k is the degree of the clique. The simulated and analytical results show that both the degree distributions of vertices and cliques follow the scale-free power-law distribution. The scale-free property of this model disappears in the absence of any one of the evolving mechanisms. Moreover, the randomicity of this model increases with the increment of the vertex number of the cliques.

Key words: scale-free; clique growth; preferential attachment; degree distribution

1 Introduction

The vertex connectivities of many lager networks such as Internet, WWW and metabolic networks follow a scale-free power-law distribution [1]. These kinds of networks are called scale-free networks because the degree of the vertices in these networks has no obvious characteristic scale [1]. BARABASI and ALBERT [2] analyzed the mechanisms of generating scale-free power-law network and proposed a scale-free network model that is called BA model. This model is the earliest and simplest scale-free network model. Later, several variations of the scale-free network model were proposed by many researchers and scholars. DOROGOVTSEV  et al [3], and KRAPIVSKY and REDNER [4] proposed a model that a constant k₀ is added in preferential attachment probability. KRAPIVSKY et al [5] proposed a model whose preferential attachment probability is nonlinear. BIANCONI and BARABASI [6] proposed a fitness model, and LI and CHEN [7] proposed a local-world evolving network model. All these scale-free network models have two basic mechanisms: (1) growth, i.e. network expands continuously by the addition of new vertices; (2) preferential attachment, i.e. new vertices attach preferentially to sites that are already well connected.

Many real complex networks have community structure feature [8-13]. Namely, these networks consist of many “clusters” or “communities”. PALLA et al [14-16] presented that networks can be composed of some cliques that are subgraphs fully connected. The research on different scale-free network models shows that the existing models are almost evolved by vertices of networks [1, 17]. There are few models that are evolved by clusters or cliques. However, many real networks are evolved by clique growth and preferential attachment. For example, if we construct a network whose vertices are the departments of every company in the world and edges are the relations between the departments, then every company is a clique. Every time step of which a new company is added into the world means that a new clique is added into the network and preferential attachment is also based on the cliques. So in this work, a novel scale-free network model was proposed based on clique growth and preferential attachment. The network expands continuously by the addition of new cliques, and new cliques attach preferentially to the old ones that are already well connected. The degree of vertices of the network generated by these mechanisms follows a scale-free power-law distribution. The degree distribution of a new network whose vertices are cliques, and edges are the connections of the cliques, also has the scale-free power-law property.

2 Presentation of model

On the basis of clique growth and preferential attachment, we proposed a novel scale-free network model as follows.

 (1) Clique growth: Starting with a small number (m₀) of cliques, at every time step we added a new clique with m edges that link the new clique to m different cliques already present in the network. Here m≤m₀, and every clique has m₁ vertices (m₁ can be selected constantly or randomly).

(2) Preferential attachment: The probability Π that a new clique is connected to clique i depends on connectivity k_i of that clique, so we have

Π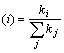                                   (1)

where the connectivity of a clique is defined like the definition of the connectivity of a vertex, which is the number of the cliques that are connected to that clique. To connect two cliques, we chose a vertex randomly in one clique and another vertex randomly in the other clique, and then connected these two vertices.

After t time steps, the model leads to a random network with N=(t+m₀)m₁ vertices and mt edges. Fig.1 shows the evolving process of the model (Only to illustrate the evolving procedure, in the later simulation, we used other value of the parameters). The initial network has two cliques, and every clique has three vertices. At every time step we added a new clique with two edges that link the new clique to two different cliques already present in the network by the mechanism of preferential attachment.

3 Characteristics of model

3.1 Degree distribution of vertices

The novel model was simulated based on clique growth and preferential attachment. Fig.2 shows the degree distribution function of vertices (P(d), d is the degree of vertex) of the model. The data of Fig.3 show the same information as Fig.2 except the value of m₁. In Fig.3 the Poisson distribution of E(m₁)=5 is chosen. According to the investigating results, it is found that many real networks are expanded by the addition of new cliques, and the number of vertices in cliques follows the Poisson distribution. So it is reasonable to choose m₁ from the Poisson distribution. At every time step a new clique of m₁ vertices is added to the model, so every vertex is joined to the model with the initial degree of m₁-1. This procedure makes the shape of the left parts of the figures.

3.2 Degree distribution of cliques

A new network can be constructed by regarding cliques as vertices and relationships between cliques as edges. The degree distribution of vertices of the new network is equal to the degree distribution of cliques of the original network. Fig.4 shows the degree distribution of cliques (P(k), k is the degree of clique) of the network generating in Section 3.1, indicating that the degree distribution of cliques also follows the scale-free power-law distribution.

3.3 Two evolving mechanisms of model

The development of the power-law scaling in the novel model indicates that clique growth and preferential attachment play an important role in network development. To verify that both mechanisms are necessary, we investigated two variants of the model. Model 1 keeps the growing character of the network, but preferential attachment is eliminated by assuming that a new clique is connected with equal probability to any clique in the network. That is

Π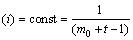                       (2)

The connection between two cliques is still to connect two vertices that are chosen randomly form these two cliques separately. Such a model (Fig.5) leads P(d) to an exponential distribution, indicating that the absence of preferential attachment eliminates the scale-free feature of the distribution.

In Model 2, we started with 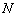cliques and no edges. At each time step, we randomly selected a clique

and connected it with probability of Π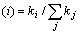to

clique 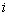 in the network. Although at early time the model exhibits power-law scaling, after t≈(N×m₁)² time steps the network reaches a state in which all cliques and all vertices are connected, because 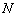is a constant and the number of edges increases with time. The failure of Models 1 and 2 indicates that both mechanisms, i.e.

Fig.1 Evolving process of proposed model (m=m₀=2, m₁=3)

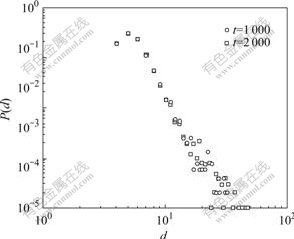
Fig.2 Degree distribution of vertices (m=m₀=5, m₁=5)

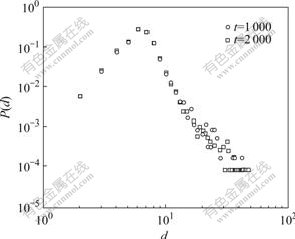
Fig.3 Degree distribution of vertices (m=m₀=5, E(m₁)=5)

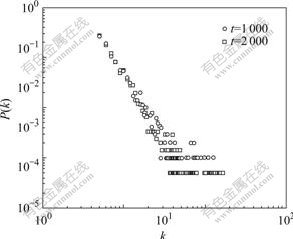
Fig.4 Degree distribution of cliques (m=m₀=5)

growth and preferential attachment of cliques are needed for the development of the scale-free power-law distribution.

3.4 Analytical results of this model

According to the mean-field theory [2, 18], the rate

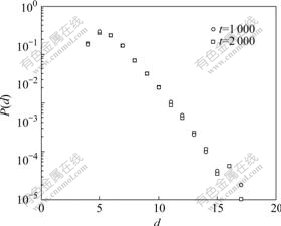
Fig.5 Degree distribution of vertices of Model 1 (m=m₀=5, m₁=5)

at which a clique acquires edges is

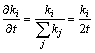                                (3)

And the initial condition is

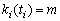                                  (4)

Eqn.(4) can be solved analytically using the method in Ref.[2]. The solution of this equation is

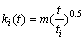                                   (5)

To get the distribution of k_i(P(k)), we transformed the equations as follows:

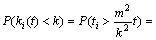
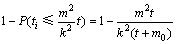                                    (6)

                             (7)

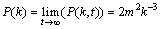
                                        (8)

Since one clique has m₁ vertices, and one vertex is chosen randomly in one clique to connect. So if we define that d is the degree of vertex, we can obtain

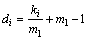                              (9)

Then we can get the degree distribution of vertices as follows:

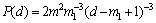
                                        (10)

When m₁=1, this model is the same as BA model. Besides, the randomicity of this model will increase with the increment of m₁.

4 Conclusions

(1) The degree distributions of vertices and cliques of the novel network model follow the scale-free distribution. It is verified that both mechanisms of clique growth and preferential attachment are necessary for the scale-free properties of this novel model. And the scale-free properties of this model will disappear in the absence of any one of the evolving mechanisms.

(2) By the mean-field theory, the degree distribution function of this model is analyzed. Moreover, the randomicity of this model increases with the increment of the vertex number of the cliques.

(3) This novel model evolves on the basis of cliques. It is different from the existing models that evolve on the basis of vertices. It has very good practical meaning because many real networks are developed by the growth and preferential attachment of cliques, not by the vertices.

References

[1] NEWMAN M E J. The structure and function of complex networks [J]. SIAM Review, 2003, 45(2): 167-256.

[2] BARABASI A L, ALBERT R. Emergence of scaling in random networks [J]. Science, 1999, 286(5439): 509-512.

[3] DOROGOVTSEV S N, MENDES J F F, SAMUKHIN A N. Structure of growing networks with preferential linking [J]. Physical Review Letters, 2000, 85(21): 4633-4636.

[4] KRAPIVSKY P L, REDNER S. Organization of growing random networks [J]. Physical Review E, 2001, 63(6): 066123.

[5] KRAPIVSKY P L, REDNER S, LEYVRAZ F. Connectivity of growing random networks [J]. Physical Review Letters, 2000, 85(21): 4629-4632.

[6] BIANCONI G, BARABASI A L. Bose-Einstein condensation in complex networks [J]. Physical Review Letters, 2001, 86(24): 5632-5635.

[7] LI X, CHEN G. A local world evolving network model [J]. Physica A, 2003, 328(1/2): 274-286.

[8] MILO R, SHEN-ORR S, ITZKOVITZ S, KASHTAN N, CHKLOVSKII D, ALON U. Network motifs: Simple building blocks of complex networks [J]. Science, 2002, 298(5594): 824-827.

[9] SHIFFRIN R M, BORNER K. Mapping knowledge domains [J]. Proc Natl Acad Sci, 2004, 101(1): 5183-5185.

[10] EVERITT B S. Cluster analysis [M]. London: Edward Arnold, 1993.

[11] KNUDSEN S. A guide to analysis of DNA microarray data [M]. New York: Wiley-Liss, 2004.

[12] NEWMAN M E J. Detecting community structure in networks [J]. The European Physical Journal B, 2004, 38(2): 321-330.

[13] CHEN Ai-bin, CAI Zi-xing, HU De-wen. Clustering in mobile ad hoc network based on neural network [J]. Journal of Central South University of Technology, 2006, 13(6): 699-702.

[14] PALLA G, DERENYI I, FARKAS I, VICSEK T. Uncovering the overlapping community structure of complex networks in nature and society [J]. Nature, 2005, 435(7043): 814-818.

[15] ADAMCSEK B, PALLA G, FARKAS I J, VICSEK T. CFinder: Locating cliques and overlapping modules in biological networks [J]. Bioinformatics, 2006, 22(8): 1021-1023.

[16] DERENYI I, PALLA G, VICSEK T. Clique percolation in random networks [J]. Physical Review Letters, 2005, 94(16): 160202.

[17] ALBERT R, BARABASI A L. Statistical mechanics of complex networks [J]. Reviews of Modern Physics, 2002, 74(1): 47-97.

[18] BARABASI A L, ALBERT R, JEONG H. Mean-field theory for scale-free random networks [J]. Physica A, 1999, 272(1/2): 173-187.

 (Edited by CHEN Wei-ping)

Foundation item: Projects(60504027, 60573123) supported by the National Natural Science Foundation of China; Project(20060401037) supported by the National Postdoctor Science Foundation of China; Project(X106866) supported by the Natural Science Foundation of Zhejiang Province, China

Received date: 2008-08-26; Accepted date: 2008-11-27

Corresponding author: WANG Wan-liang, Professor, PhD; Tel: +86-571-88320491; E-mail: wwl@zjut.edu.cn