基于支持向量回归机的空调逐时负荷滚动预测算法
周璇1, 2,杨建成1, 2
(1. 华南理工大学 机械与汽车工程学院,广东 广州,510640
2. 广东省城市空调节能与控制工程技术研究开发中心,广东 广州,510640)
摘要:针对当前空调负荷预测算法精度不高难以满足空调系统节能优化控制的问题,提出基于支持向量回归机(Support Vector Regression,SVR)的空调逐时负荷滚动预测算法,建立SVR滚动预测模型,模型参数采用网格搜索遍历算法进行寻优。为简化模型的复杂性,还对影响空调负荷的主要因素进行了相关性分析。此外,算法利用当日前1 h的滚动信息,不断对模型进行修正以提高负荷预测精度。最后探讨以期望误差为预测精度评价指标时,不同训练样本长度对神经网络和SVR算法预测精度的影响。预测结果表明:基于支持向量回归机的空调逐时负荷滚动预测算法较BP神经网络算法的预测精度提高10.3%,比常规支持向量回归机算法预测精度提高23.9%,训练样本较小时,算法预测性能更为优越。
关键词:空调逐时负荷;滚动预测算法;支持向量回归机;网格搜索遍历算法;期望误差
中图分类号:TP181;TU831 文献标志码:A 文章编号:1672-7207(2014)03-0952-06
An algorithm for hourly load rolling forecasting of air conditioning system based on SVR
ZHOU Xuan1, 2, YANG Jiancheng1, 2
(1. School of Mechanical & Automotive Engineering, South China University of Technology,
Guangzhou 510640, China;
2. City Air-conditioning Energy Conservation and Control Project Technology Research Exploitation Center of Guangdong, Guangzhou 510640, China)
Abstract: For load prediction algorithm accuracy of air conditioning system is not high enough to fulfill the requirement of energy optimal control for energy conservation, a support vector regression (SVR) model and its algorithm for hourly load rolling forecasting were proposed in this paper, with the parameters optimized by mesh optimization algorithm. Moreover, the correlation analysis was used to analyze the main factors affecting the load of air conditioning system to simplify the model and the previous 1-hour load and weather information were used to modify the model in the forecasting process continuously. Furthermore, the effect of training-sample size on prediction accuracy was discussed. Finally, as expected error percentage was adopted as the evaluation of the prediction accuracy, the results showed that the prediction accuracy of rolling forecasting algorithm based on support vector regression was 10.3% and 23.9% more accurate than BP neural network algorithm and conventional SVR algorithm respectively when the number of the training set is 3 672, which was better with little training sample set.
Key words: hourly load of air conditioning system; rolling forecasting algorithm; support vector regression; mesh optimization algorithm; expected error
随着社会经济的发展,空调系统能耗与夏季高峰负荷逐年上升,空调系统节能成为当今社会实现可持续发展的关注热点之一。提高空调负荷预测的准确性是实现空调系统节能运行和优化控制的基础和前提条件。现有空调负荷预测大多用于建筑空调系统与冰蓄冷空调系统的设计、优化运行与节能控制等方面,常用的预测算法有时间序列算法、人工神经网络算法以及支持向量回归机(SVR)算法等。蒋小强等采用改进的人工神经网络算法建立了区域供冷系统逐时冷负荷预测模型,预测次日24 h冷负荷[1]。Kamimura等[2]提出了融合拓扑案例模型(TCBM)和综合自回归移动平均(ARIMA)的新模型预测空调负荷,以优化蓄热系统的运行。Nakahara等[3]比较了卡尔曼滤波器、GMDH方法和神经网络3种负荷预测模型的预测精度,在输入变量选择,基准数据前处理方法以及预测公式的形式对预测精度的影响等方面进行了讨论。李元旦[4]对比了单纯时间序列模型、传递函数模型和神经网络负荷预测3种方法的预测精度,认为人工神经网络方法虽然具有预测精度较高、推广能力较强等特点,但是由于人工神经网络对训练样本数量有较高要求,其泛化能力有时不理想。支持向量机具有强大的非线性映射特性,近年来在空调负荷预测领域应用较广泛。Li等[5]建立了典型气象年气象参数条件下某办公建筑的建筑物逐时冷负荷的支持向量机和BP神经网络预测模型,比较了两种模型的预测精度;Li等[6-7]提出了基于最小二乘支持向量机(LS-SVM)的建筑逐时冷负荷预测模型以及融合ARIMA和SVR的建筑物冷负荷预测模型。上述基于支持向量机的空调负荷预测方法大多仅利用预测日前一日或更长时间段的负荷数据与天气预报数据等建立相应模型,并不利用当日已知信息对模型进行修正,但是根据近大远小的原理,预测当日的已知信息对预测结果影响更大。因此,本文作者提出了基于SVR的空调系统逐时负荷滚动预测方法,在SVR模型中滚动地引入最新获得的负荷和气象信息,对模型不断进行修正以提高其预测精度,解决空调负荷预测算法精度不高,难以满足空调系统节能优化控制的问题。最后利用1997年日本空气调和卫生工学会(SHASE)举办负荷预测竞赛所提供的Trail-2数据,验证空调逐时负荷滚动预测模型和算法的有效 性,并讨论不同训练样本长度对不同算法预测精度的影响。
1 支持向量回归机原理
支持向量机通过非线性映射 将输入向量映射到高维特征空间H中,运用结构风险最小化原则构造最优决策函数,并巧妙地利用原空间的核函数取代高维特征空间的点积运算。支持向量回归机是支持向量在函数回归领域的应用。ε-SVR是一种常用的支持向量回归机,通过引入ε不敏感损失函数实现具有较强鲁棒性的回归,而且回归估计是稀疏的,保留了SVM的所有优点[8]。
将输入向量映射到高维特征空间H中,运用结构风险最小化原则构造最优决策函数,并巧妙地利用原空间的核函数取代高维特征空间的点积运算。支持向量回归机是支持向量在函数回归领域的应用。ε-SVR是一种常用的支持向量回归机,通过引入ε不敏感损失函数实现具有较强鲁棒性的回归,而且回归估计是稀疏的,保留了SVM的所有优点[8]。
给定训练集 ,
, ,
, ,l为训练样本总数;在高维空间H,构造回归函数为
,l为训练样本总数;在高维空间H,构造回归函数为
 (1)
(1)
式中: 为Rn空间到Hilbert空间的变换;w为权值向量,
为Rn空间到Hilbert空间的变换;w为权值向量, ;b为截矩,
;b为截矩, 。
。
引进惩罚参数C和不敏感损失函数 ,将回归问题转化为如下关于变量w和b的凸二次规划问题:
,将回归问题转化为如下关于变量w和b的凸二次规划问题:
 (2)
(2)
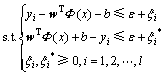
式中: 和
和 为松弛变量。
为松弛变量。
利用拉格朗日函数和对偶原理,并引入核函数 加以变换,得到式(2)的对偶问题:
加以变换,得到式(2)的对偶问题:

 (3)
(3)
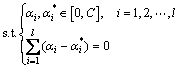
通过式(3)求解 和
和 ,最终得到决策函数:
,最终得到决策函数:
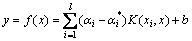 (4)
(4)
由于径向基函数能够很好地将样本集从输入空间非线性映射到高维特征空间,具有良好的处理样本输入与输出之间复杂非线性关系的能力,并且具有参数变量少、参数选取计算量较小和计算效率高等优点[9]。本文选取径向基内积函数 为SVR核函数。
为SVR核函数。
2 负荷预测对象描述
本文所用数据来源于1997年日本空气调和卫生工学会(SHASE)举办负荷预测竞赛所提供的Trail-2数据,Trial-2数据主要验证各种预测模型在实际控制应用中的可行性。研究对象为东京的一栋综合性办公建筑,建筑面积5 404 m2,共9层。底层用于停车,办公室、餐厅和银行在2~3层,4~9层为出租办公楼。建筑冷热源设备包括2台空气源盐水冷水机组/热泵,最大制冷量102 kW/台,最大制热量212 kW/台,蓄冷蓄热容量64 m3,夏季用于蓄冷,冬季用于蓄热。暖通空调系统为单风道变风量空调系统,空调末端设备为空调机组(AHU)和风机盘管(FCU),每层均有布置。
Trial-2数据包括1995-06-01—1995-10-31以及1996-06-01—1996-10-31的室外逐时气象参数、室内逐时环境参数、建筑空调末端设备逐时开关状态及空调冷负荷的逐时数据以及室外逐日气象参数预报值。其中室外逐时气象参数包括室外干球温度、室外相对湿度与太阳总辐射,室内逐时环境参数包括每层楼FCU的回风温度与AHU的回风温度、相对湿度(风机盘管无回风相对湿度检测值),空调末端设备逐时开关状态包括每层楼FCU和AHU的开关状态。室外逐日气象参数预报值包括当日室外最低干球温度、最高干球温度与最低相对湿度的预报值。
3 应用研究
本文将数据样本分为训练样本和预测样本2部分,训练样本为1995-06-01—1995-10-31的3 672个训练样本,待预测样本为1996-06-01—1996-10-31的3 672个预测数据。空调系统逐时负荷预测建模、模型训练及预测算法实现等均在Matlab平台下利用LIBSVM工具箱中的epsilon-SVR实现。
3.1 输入变量选择
空调负荷随着建筑物围护结构、室外气象参数、室内环境参数、空调末端设备开启状态等诸多因素的变化而变化,影响空调负荷的因素极为复杂。为了降低模型的复杂性,本文以1995-06-01—1995-10-31的数据为基准,对建筑物空调负荷与多个影响因素利用SPSS软件进行了相关性分析,通过常用的Pearson 相关系数和双侧显著性检验(T统计量,显著性概率P<0.01)得到的相关系数分析结果见表1。
其中,AHU和FCU的逐时开启数量由AHU和FCU的开启状态统计获得。此外,办公类建筑内人员密度、灯光散热等的变化具有一定的规律,该规律与日期星期类型及运行时刻密切相关[4]。同时考虑到建筑空调系统具有大惯性,无法突变,前1 h的基准负荷与当前时刻负荷间存在强烈的相关性。本文对日期星期类型、运行时刻及前1 h的基准负荷与当前时刻基准负荷的相关性也进行了分析。文献[3]将当日室外最高和最低温度预报值作为输入变量,为比较负荷预测精度,本文也对当日室外最高、最低温度及最低相对湿度预报值进行了相关性分析。
表1 输入变量与基准负荷的相关系数
Table 1 Correlation coefficient of input variables and measurement load

由表1可知:AHU和FCU逐时运行数量、室外逐时干球温度、室外逐时太阳总辐射、室外逐时相对湿度、前1 h基准负荷、当前时刻、日期星期类型均与基准负荷的相关性强度较高。但是,对于实际工程应用,由于预测时刻的参数值无法获取,本文选择前1 h AHU和FCU逐时运行数量、前1 h室外逐时干球温度、前1 h室外逐时太阳总辐射、前1 h的室外逐时相对湿度、当前运行时刻、日期星期类型及前1 h的基准负荷作为输入变量,输出变量为逐时基准负荷。由于室外气象参数预报值受到气象参数预报准确性的影响,文献[3]中提及的室外气象参数预报值的相关系数要小于当日室外逐时气象参数值。
3.2 数据归一化处理
为了提高计算效率,防止计算过程中出现个别数据溢出的不良现象,将输入输出数据进行归一化处理,处理成[0,1]的无因子数,处理方法如下:
 (5)
(5)
 (6)
(6)
式中:k=1, 2, …, l (l为样本总数); d=1, 2, …, m (m为输入变量总数); 和
和 为归一化后第k个样本中第d个输入和输出变量数值;
为归一化后第k个样本中第d个输入和输出变量数值; 和
和 为第i个样本中第d个输入和输出变量数值;
为第i个样本中第d个输入和输出变量数值; 和
和 为样本数据中第d个输入和输出变量最小值;
为样本数据中第d个输入和输出变量最小值; 和
和 为样本数据中第d个输入和输出变量最大值;
为样本数据中第d个输入和输出变量最大值;
3.3 SVR预测模型参数选择
参数选择对SVR模型的预测性能有很大的影响,目前SVR参数寻优常用的方法为网格搜索遍历法。本文采用网格搜索法和K-折交叉验证法对参数C和 [10-12]进行优化,为了缩短优化过程,网格搜索采用粗网格和细网格划分相结合的方式进行。
[10-12]进行优化,为了缩短优化过程,网格搜索采用粗网格和细网格划分相结合的方式进行。
根据分布情况及经验分别设置C, 参数的取值范围与
参数的取值范围与 的取值[13-15],设定C和
的取值[13-15],设定C和 的取值范围为[2-8 28],选择
的取值范围为[2-8 28],选择 。将训练样本集分为5等分,4份用于学习,1份用于验证,交替进行直至遍历整个评价集,选择出与最小MSE(mean squared error)平均值对应的各参数值作为优化的参数值。各参数优化结果如图1所示。SVR预测模型参数优化结果:C=4,
。将训练样本集分为5等分,4份用于学习,1份用于验证,交替进行直至遍历整个评价集,选择出与最小MSE(mean squared error)平均值对应的各参数值作为优化的参数值。各参数优化结果如图1所示。SVR预测模型参数优化结果:C=4, =4。
=4。
3.4 评价指标
本文采用期望误差EEP作为评价指标,EEP的计算如方程(7)所示,E EP越小,证明负荷预测精度越高。
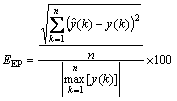 (7)
(7)
其中:y(k)为当前时刻的实际负荷;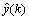 为当前时刻的预测负荷;
为当前时刻的预测负荷;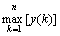 为最大的实际负荷;n为负荷预测时间。
为最大的实际负荷;n为负荷预测时间。
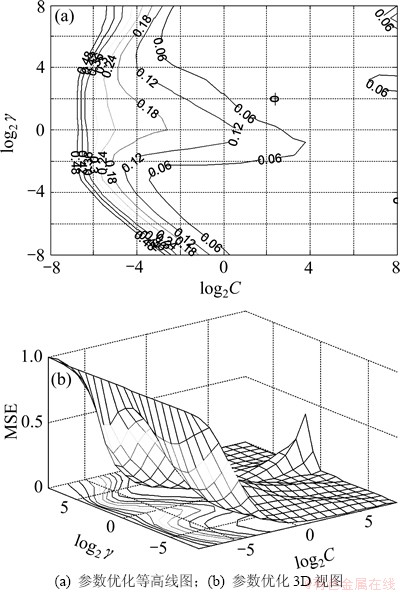
图1 网格搜索法SVR模型参数优化
Fig. 1 Parameter optimization of SVR model by mesh optimization algorithm
4 预测算法实现与结果分析
4.1 滚动预测算法实现
本文提出的滚动预测算法具体步骤如下:
(1) 选择输入、输出变量;
(2) 数据归一化处理;
(3) 参数寻优:SVR训练模型的惩罚系数与径向基核函数参数 寻优;
寻优;
(4) 初始建模:建立SVR预测初始模型,i置初值,i=0;
(5) i=i+1,预测下一时刻负荷:利用当前时刻的输入数据和SVR负荷预测模型,预测得到下一时刻的负荷,将预测结果反归一化处理,并输出;
(6) 更新训练样本:训练样本中增加当前时刻的实际输入、输出数据,丢弃最远时刻的样本数据;
(7) 更新模型:在线更新SVR训练模型;
(8) 重复步骤(5)~(7)直至预测过程结束。
4.2 滚动预测算法应用
选取1996-06-01—1996-10-31共153 d作为待预测时段,本节分别采用了神经网络、常规SVR算法以及SVR滚动算法,在相同的输入输出变量训练条件下比较其预测精度,并与文献[3]提出的神经网络预测精度进行了比较,建立的神经网络模型与文献[3]的不同之处在于输入变量的选择不同,如表2所示。同时,对不同训练样本长度下各预测模型的预测精度进行了比较,预测精度见表3所示。选取1996-08-03—1996-08-09这1周的空调逐时负荷作为待预测对象,图2和3所示分别为训练样本长度为3 672和168 2种情况下3种预测算法在7 d内逐时预测负荷和实际负荷的比较。
表2中,d表示当日,d-1表示前一日,k表示当前时刻,k-1表示前一时刻。
表2 不同预测模型的输入变量
Table 2 Input variables of four predictive models

表3 不同训练样本长度下空调逐时负荷预测结果EEP比较
Table 3 Hourly air conditioning load forecasting results EEP with different training sample lengths

4.3 预测结果比较与分析
4.3.1 训练样本长度对不同负荷预测模型预测精度的影响
图2所示为训练样本长度3 672下3种预测模型预测负荷和实际负荷的比较。可见:当训练样本长度为3 672时,神经网络、常规SVR和SVR滚动模型的预测精度都较好,EEP最佳预测精度均在7以下。其中,基于SVR的逐时负荷滚动预测算法精度比文献[3]的神经网络逐时负荷预测算法精度高19.6%,比相同输入变量条件下的神经网络预测模型的精度高10.3%。
图3所示为训练样本长度168下3种预测模型预测负荷和实际负荷的比较。可见:当训练样本长度为减少到720(30天)时,SVR滚动模型的预测精度降低了12.5%,常规SVR模型预测精度降低了59.9%,神经网络预测精度降低了134.3%;当训练样本长度为减少到168(1周)时,SVR滚动模型的预测精度降低了31.1%,常规SVR模型预测精度降低了131.7%,神经网络预测精度降低了231.0%,从图3可见:在训练样本较少时,常规SVR模型的预测精度要小于神经网络模型预测精度,且远远小于SVR滚动预测模型的预测精度。
随着训练样本长度的减少,3种预测模型的预测精度均呈下降趋势,其中SVR滚动模型预测精度变化范围最小,预测精度也最高,其次为神经网络模型,常规SVR模型受训练样本长度的影响最大。

图2 训练样本长度3 672下3种预测模型预测负荷和实际负荷的比较
Fig. 2 Comparisons of forecast load and actual load with length of training sample of 3 672

图3 训练样本长度168下3种预测模型预测负荷和实际负荷的比较
Fig. 3 Comparisons of forecast load and actual load with length of training sample of 168
办公建筑空调负荷影响因素复杂,当训练样本数据量较少时,会出现训练不足(欠学习)的情况,难以保证神经网络和常规SVR模型的精度。而滚动预测算法中不断引入前一时刻的数据对模型进行修正,能够保持较高的训练精度。由此可见,在训练样本较少时,SVR滚动模型具有更优越的预测性能。
4.3.2 输入变量的影响
本文的输入参数引入了前一时刻的室外气象参数实际值,而文献[3]中输入参数引入了当日室外最低、最高干球温度的天气预报值,由表3可知:当训练样本数量为3 672时,以前一时刻室外气象参数实际值为输入比天气预报值为输入的空调负荷预测精度提高了10%,降低了天气预报信息不准确对空调负荷预测精度的影响。
5 结论
针对空调节能优化控制对空调负荷预测精度要求较高的问题,提出基于SVR的空调逐时负荷滚动预测模型的建模方法和预测算法,并讨论模型参数的优化、模型输入的选择以及不同训练样本长度对预测精度的影响等问题。预测结果表明,当训练样本较大时,基于SVR的空调逐时负荷滚动预测方法较神经网络预测算法和常规SVR预测算法预测精度分别提高了10.3%和23.9%,预测精度较高,当训练样本较少时,本文提出的滚动预测算法预测性能更为优越。
参考文献:
[1] 蒋小强, 龙惟定, 李敏. 区域供冷系统逐时冷负荷的分析及数值预测[J]. 中南大学学报(自然科学版), 2010, 41(1): 357-363.
JIANG Xiaoqiang, LONG Weiding, LI Min. Hourly cooling load analysis and prediction in a district cooling system[J]. Journal of Central South University (Science and Technology), 2010, 41(1): 357-363.
[2] Kamimura K, Matsuba T, Tsutsui H. Development of load profile prediction using TCBM and ARIMA hybrid- modeling[C]// Building Simulation, Kyoto, Japan, 1999: 909-916.
[3] Nakahara N, Zheng M, Pan S, et al. Load prediction for optimal thermal storage-comparison of three kinds of model application[C]// Building Simulation. Kyoto, Japan, 1999: 519-526.
[4] 李元旦. 建筑物空调负荷预测方法及冰蓄冷空调系统运行优化控制研究[D]. 上海: 同济大学机械与能源工程学院, 2002: 22-62.
LI Yuan-dan. Research on building's air-conditioning load prediction and optimal control strategy of ice thermal storage system [D]. Shanghai: Tongji University. School of Mechanical Engineering, 2002: 22-62.
[5] LI Qiong, MENG Qinglin, CAI Jiejin, et al. Predicting hourly cooling load in the building: A comparison of support vector machine and different artificial neural networks [J]. Energy Conversion and Management, 2009, 50(1): 90-96.
[6] LI Xuemei, LU Jinhu, DING Lixing, et al. Building cooling load forecasting model based on LS-SVM[C]// Asia Pacific Conference on Information Processing. Shenzhen, China, 2009: 55-58.
[7] LI Xuemei, DING Lixing, DENG Yuyuan, et al. Hybrid support vector machine and ARIMA model in building cooling prediction[C]// Computer Communication Control and Automation (3CA). Taiwan, 2010: 533-536.
[8] Hoogenboom G, McClendon R, Paz J. Support vector regression with reduced training sets for air temperature prediction: A comparison with artificial neural networks[J]. Neural Computing and Applications, 2011, 20(1): 151-159.
[9] Nanye L, Daniel G, Guilherme J, et al. Application of support vector regression to genome-assisted prediction of quantitative traits[J]. Theoretical and Applied Genetics November, 2011, 123(7): 1065-1074.
[10] 史峰, 王小川, 郁磊, 等. MATLAB神经网络30个案例分析[M]. 北京: 北京航空航天大学出版社, 2010: 122-140.
SHI Feng, WANG Xiaochuan, YU Lei, et al. MATLAB neural network analysis of 30 cases[M]. Beijing: Beijing University of Aeronautics and Astronautics Press, 2010: 122-140.
[11] Chang C, Lin C. LIBSVM: A library for support vector machines[J]. ACM Transactions on Intelligent Systems and Technology, 2011, 2(3): 1-27.
[12] 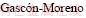 J, Salcedo-Sanz S,
J, Salcedo-Sanz S,  E, et al. New validation methods for improving standard and multi-parametric support vector regression training time[J]. Expert Systems with Applications, 2012, 39(9): 8220-8227.
E, et al. New validation methods for improving standard and multi-parametric support vector regression training time[J]. Expert Systems with Applications, 2012, 39(9): 8220-8227.
[13] Ustun B, Melssen W, Oudenhuijzen M, et al. Determination of optimal support vector regression parameters by genetic algorithms and simplex optimization[J]. Analytical Chimica Acta, 2005, 544(1/2): 292-305.
[14] He W, Wang Z, Jiang H. Model optimizing and feature selecting for support vector regression in time series forecasting[J]. Neurocomputing, 2008, 72(1/2/3): 600-611.
[15] Ding L,  J, Li X. Support vector regression and ant colony optimization for HVAC cooling load prediction[C]// 3CA 2010 - 2010 International Symposium on Computer, Tainan, 2010: 537-541.
J, Li X. Support vector regression and ant colony optimization for HVAC cooling load prediction[C]// 3CA 2010 - 2010 International Symposium on Computer, Tainan, 2010: 537-541.
(编辑 陈爱华)
收稿日期:2013-03-20;修回日期:2013-06-10
基金项目:广东省科技厅项目(2011B061200043)
通信作者:周璇(1976-),女,江西波阳人,博士,副研究员,从事空调负荷预测研究;电话:020-87110835;E-mail: zhouxuan@scut.edu.cn