Effect of evolution of polycrystalline textures on
r-value of LF2 aluminum alloy

ZHAO Yi-xi(赵亦希), LIN Zhong-qin(林忠钦), LI Shu-hui(李淑慧), YU Zhong-qi(于忠奇)

School of Mechanical Engineering, Shanghai Jiao Tong University, Shanghai 200240, China

Received 28 July 2006; accepted 15 September 2006

Abstract: The effect of evolution of polycrystalline texture on normal anisotropy coefficient r-value of aluminum alloy sheet was investigated. For this purpose, the textures under different elongation of LF2 aluminum alloy were measured and analyzed. The result indicates that the initial texture of LF2 aluminum alloy has the typical rolling texture, and the main components include Brass {011}〈211〉, Copper {112}〈111〉and S{123}〈634〉. These three main components exhibit different transformation tendencies when the material specimens are stretched along the different direction. Based on Taylor model and Minor Work principle, the normal anisotropy coefficient r-values of polycrystalline aluminum alloy under various strain states were calculated. The result indicates that the r-values of LF2 aluminum alloy vary with tensile direction and the amount of deformation. The deformability on rolling direction is superior to the other direction because an enhancement tendency of r₀ appears in tension process along rolling direction.

Key words: polycrystalline texture; normal anisotropy coefficient; uniaxial tensile; deformability; LF2 aluminum alloy

1 Introduction

Now aluminum alloy has come forward as a major solution to the mass problem in modern vehicle industry, and its low density and high strength mean that aluminum alloy parts weigh much less than traditional materials such as steel. But aluminum alloy shows drawbacks such as narrower forming window, severer springback and less formability than steels in forming process, which to some degree restricts the extensive application of aluminum alloy[1-2]. Now there is a growing interest in the industry and academic to improve the formability of aluminum alloy.

The evolution of anisotropic properties and formability during deformation has been regarded as an important subject in metal forming process[3-7]. The normal anisotropy coefficient, r, is an important index to evaluate anisotropy, which is mainly controlled by formation of preferred orientation or polycrystalline texture. The higher r-value is, the better the formability is. Many researches showed that the texture change will be affected not only by strain but also by strain path. The crystallographic texture evolution by plastic deformation such as tension, rolling, deep drawing[8-14], was experimentally investigated and theoretically predicted both in micro-scopic and macroscopic scales. But how to control texture evolution to improve the formability is still quit difficult. r-value will change with the deformation of material, and the relationship among texture, r-value and formability is not very clear. In this study, the effect of crystallographic texture evolution on the normal anisotropy coefficient of LF2 aluminum alloy is studied in theory and experiment. The influence of changes in metallurgical characteristics on inherent formability will be better understood.

2 Experimental

Texture analysis was carried out after uniaxial tensile test using sheet samples of LF2 aluminum alloy with 1 mm in thickness.

The standard tensile specimens under ASTM specifications were taken from the sheets in 0?, 45?, 90? along rolling direction. The specimens were stretched to 5% and 10% elongation along each direction respectively.

The textures were measured by means of standard X-ray diffraction technology. The texture specimens were cut to size of 10 mm×20 mm from the uniform deformation parts of tensile specimens. Three incomplete pole figures {111}, {220} and {200} were determined using a surface detection X-ray diffraction instrument and the orientation distribution functions (ODFs) were calculated.

3 Texture evolution of LF2 aluminum alloy

3.1 Initial texture analysis

According to the ODF maps (Fig.1) and the key orientation distributions[15] (Fig.2), it’s easy to conclude that the LF2 aluminum alloy has typical rolling texture. The texture orientations mainly focus on Brass {011} 〈211〉, Copper {112}〈111〉 and S {123}〈634〉, and the intensity of Gauss {011}〈100〉is small.

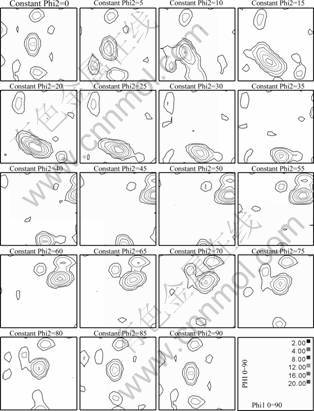
Fig.1 ODFs of original texture

In the deforming process the orientation of crystal grain will show tendencies to congregate on some fiber orientations in Euler space, such as α-fiber and β-fiber orientation. The α-fiber orientation extends from φ₁=0?-90?, =45?, φ₂=90? or 0?, the β-fiber orientation extends from φ₂=45? to φ₂=90? section of Euler space.

For initial sheet the orientations on α-fiber mainly focuses on the Brass（35?，45?，0?）, while Copper {112} 〈111〉 and S{123}〈634〉 are concentrated around β-fiber(Fig.3 and Fig.4).

3.2 Evolution of texture induced by tension

The textures of specimens with 5% and 10% elongation along the rolling direction (RD, 0?), diagonal

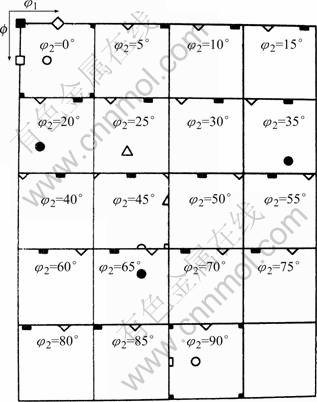
Fig.2 Key orientations on ODF figure: ■ Cube{001}〈100〉; □ Gauss{011}〈100〉; ● R{123}〈211〉; ○ Brass{011}〈211〉; ◇ Rotary cube{011}〈110〉; △ Brass-R{111}〈211〉

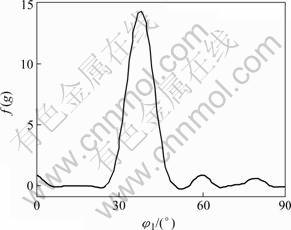
Fig.3 a-fiber orientation of initial texture

direction (DD, 45?) and transverse direction (TD, 90?) were analyzed.

When the specimens are stretched along RD (Fig.5), the main orientation on the α-fiber is Brass(35?, 45?, 0?). The other orientations on the α-fiber gradually concentrate on Brass and increase the intensity of Brass. The main orientations on β-fiber are still Copper and S (Fig.6), and the intensity and congregation degree of them increase with the elongation increasing.

Brass orientation is still the main orientation on α-fiber orientation in DD and TD tension. But a decreasing congregation tendency of Brass is found in DD tension, while an increasing congregation tendency in TD tension is found when the deformation degree is increased.

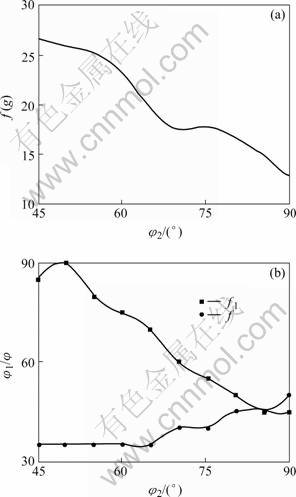
Fig.4 β-fiber orientation of initial texture

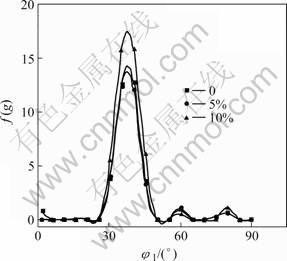
Fig.5 β-fiber orientation with 0%, 5%, 10% elongation along RD

Copper {112}〈111〉 and S{123}〈634〉, as the main components, still appear on β-fiber regardless of DD or TD. In DD tension the congregation degree of these two orientations gradually decreases. Some changes happen in the TD tensile process. The congregation degree of Copper {112}〈111〉 shows a drop earlier and raising later, and S{123}〈634〉 can convert to (50?, 45?, 80?) via (55?, 40?, 75?).

Fig.6 b-fiber orientation with 0%, 5%, 10% elongation along RD (lines of 0% elongation and 5% elongation in (b) and (c) are overlapped)

4 Effect of texture evolution on r-value of LF2 aluminum alloy

  4.1 r-value model

A Taylor model is adopted, in which the deformation in each grain is taken to be identical to the macroscopic deformation of the continuum[16-17]. When taking into account of the relationship that the strain tensor should be met, the simplification is made that a single crystal deformation under plane strain state is a single slip system process.

The normal anisotropy coefficient r-value of arbitrary angle α along RD in a single crystal should be[15]

                             (1)

where  n₂ and n₃ are the fraction of normal unit vector of slip plane, b₂ and b₃ are the fraction of unit vector of slip direction. The subscripts 2, 3 present normal direction and the third direction perpendicularly to the tensile direction, respectively.

The r-value of polycrystal is presented by

                            (2)

where  q is the shrinkage ratio, α is the angle between tensile direction and rolling direction. Using the Minor Work principle q_min(α) can be solved [15-17].

4.2 Discussion of r-value

4.2.1 r-value of typical orientations in a single crystal system

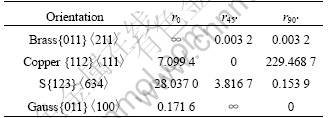
The r-values of typical orientations of LF2 aluminum alloy are calculated, as listed in Table 1.

All these three main orientations, Brass, Copper and S, have bigger r₀ value and smaller r_45? value. Gauss texture has a bigger r_45? value, but its volume fraction is smaller. A simple estimation is that the r-value order in three direction of LF2 aluminum alloy is r₀＞r_90?＞r_45?.

Table 1 r-values of important texture orientations

Similar to the ODFs, the distribution maps of r-values in the Euler space should be drawn as r(g) values on each orientation calculated in certain direction. The main orientations to influence r₀ value are S, Copper and Brass. When the deformation amount increases, three of them all enhance because the volume fraction and congregating degree of them increase, so r₀ value presents an increasing tendency along RD tension. Fig.7 presents the r(g) distribution of initial texture and the results are listed in Table 2.

Table 2 Change of r(g) under different tension states

4.2.2 r-value of polycrystalline material under uniaxial tension

The r-value measurement tests were done to verify the validity of the model. The general change trend is coincident between experiments and the calculated result (Fig.8).

Fig.7 Distribution of r(g) in Euler space: (a) r₀(g); (b) r_45?(g); (c) r_90? (g)

Based on above analysis and the texture data, the r-values of arbitrary angle along RD can be calculated and comprehensive information about material anisotropy should be achieved. Considering the symmetry, r-values between 0? and 90? tensile angle along RD are sketched in Fig.9. In fact the two peak r values appear at about 20? and 75? respectively.

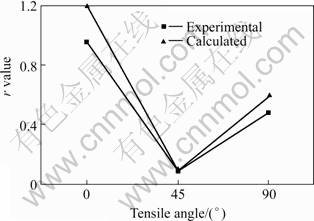
Fig.8 Comparison of r-value between experiment and texture theory

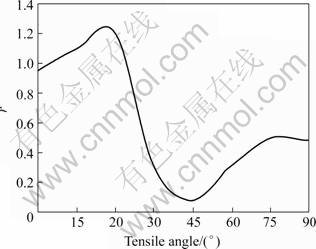
Fig.9 Variation of r-values with different tensile directions based on texture data

The r-value will not keep constant once the texture distributions change. Fig.10 shows the change of the r-value distributions under different tensile directions. All of the three r-values appear an earlier decreasing and a latter increasing trend, but r_90? value at 10% elongation is lower than that in the initial state. In all of three parameters, the r_45? value has a smallest fluctuation. Small thinning ratio occurs at 0°tension because a higher r-value is obtained after stretching, which means the deformation ability of LF2 aluminum alloy in rolling direction is superior to the other directions.

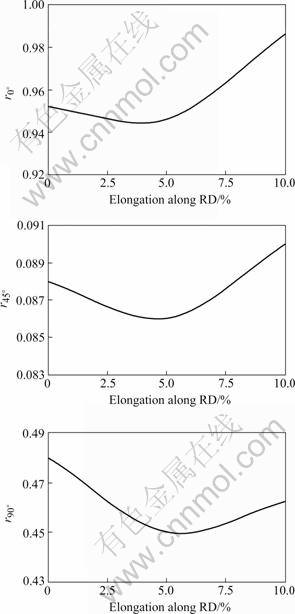
Fig.10 Variation of r-values with different elongations

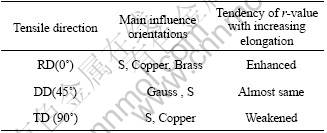
5 Conclusions

1) LF2 aluminum alloy has typical initial rolling textures, which will be transformed along the deformation degree. The main initial textures will be enhanced along RD tension and decreased along DD tension.

2) The texture evolution at different elongation and directions affects the anisotropy coefficient r-values of material. The quantitative calculations indicate the r-values will change with the deformation amount, and deformation ability of LF2 aluminum alloy on rolling direction is superior to the other directions.

3) The normal anisotropy r-value is an important parameter to affect the formability of material. This research is helpful to understanding the anisotropy property of the material in essential and give hints in formability improvement in aluminum alloy.

References

[1] HAYASHI H, NAKAGAWA T. Recent trends in sheet metals and their formability in manufacturing automotive panels[J]. JMPT Technical Paper, 1994, 46: 455.

[2] STORY J M, JARVIS G M. Issues and trends in automotive aluminum sheet forming[Z]. SAE Technical Paper, 930277.

[3] SUH Y S, SAUNDERS F I, WAGONER R H. Anisotropic yield functions with plastic-strain-induced anisotropy[J]. International Journal of Plasticity, 1996, 12(3): 417-438.

[4] LOPES A B, BARLAT F. Effect of texture and microstructure on strain hardening anisotropy for aluminum deformed in uniaxial tension and simple shear[J]. International Journal of Plasticity, 2003, 19: 1-22.

[5] HU J G, JONAS J J. ZHOU Y D, ISHIKAWA T. Influence of damage and texture evolution on limit strain in biaxially stretched aluminum alloy sheets[J]. Materials Science and Engineering A, 1998, 251: 243-250.

[6] HU J G, ISHIKAWA T, IKEDA K. Analysis on earing behavior of textured pure aluminum and A5083 alloy sheets[J]. Journal of Materials Processing Technology, 1998, 83: 200-208.

[7] BRYANT J D. Effect of crystallographic texture on formability in AA611 auto-body sheet[A]. Proceedings of the TMS Materials Week′95 Symposium, Aluminum and Magnesium for Automotive Application[C]. The Minerals, Metals & Materials Society, 1996: 85-95.

[8] HIGGINSON R L. Strain path effects on texture development in aluminium[J]. Materials Science Forum, 2002, 396: 303-308.

[9] SAVOIE J, ZHOU Y. Textures induced by tension and deep drawing in aluminum sheets[J]. Acta Mater, 1996, 44(2): 587-605.

[10] VANKUDRE H V, DATE P P, SAMAJDAR I, YERRA S K. Effect of in-plane biaxial strain paths on the variation of normal anisotropy and texture of steel sheet[J]. JMPT, 2002, 125/126: 756-763.

[11] YOON J W, BARLAT F, GRACIO J J, RAUCH E. Anisotropic strain hardening behavior in simple shear for cube textured aluminum alloy sheets[J]. International Journal of Plasticity, 2005, 21: 2426-2447.

[12] KLM K H, LEE D N. Analysis of deformation textures of asymmetrically rolled aluminum sheets[J]. Acta Mater, 2001, 49: 2583-2595.

[13] KNOCKAERT R, CHASTEL Y. Experimental and numerical determination of texture evolution during deep drawing tests[J]. Journal of Materials Processing Technology, 2001, 110: 300-311.

[14] PANCHANADEESWRAN S, FIELD D P. Texture evolution during plane strain deformation of aluminum[J]. Acta Metal Mater, 1995, 43(4): 1683-1692.

[15] MAO Wei-ming. The Crystal Texture and Anisotropy of Metals[M]. Beijing: Science Press, 2002. 201-203.

[16] TAYLOR G I. Plastic strain in metals[J]. Inst Met, 1938, 62: 307-324.

[17] LIN T H. Plastic deformation of BCC polycrystals[J]. Mech Phys Solids, 1964, 12: 25-33.

(Edited by YANG Bing)

Foundation item: Project(50225520) supported by the National Natural Science Foundation of China

Corresponding author: ZHAO Yi-xi; Tel: +86-21-34206304; E-mail: yxzhao@sjtu.edu.cn