DOI:10.19476/j.ysxb.1004.0609.2017.04.020
椭圆型混合器内二元颗粒径向混合
张立栋1,李连好1,王 擎1,秦 宏1,李少华2
(1. 东北电力大学 能源与动力工程学院,吉林 132012;
2. 中国大唐集团科学技术研究院有限公司,北京 102206)
摘 要:采用实验和理论分析方法,以Lacey混合指数作为混合评价指标,研究转速、填充率对椭圆型混合器内二元颗粒在滚落运动模式下径向混合的影响。结果表明:在波动混合阶段,椭圆型混合器的离心率影响颗粒的混合稳定性;同一工况下,椭圆型混合器在竖直位置和水平位置的颗粒动态休止角相等;填充率一定时,动态休止角随转速的增大而增大;填充率不大于1/2、转速一定时,同一位置的活动层自由下滑面长度随填充率的增大而增大;同一工况下,椭圆型混合器在竖直位置时的活动层面积大于水平位置时;位置一定时,活动层面积随填充率增大而减小,随转速增大而增大;当转速不变,颗粒的混合程度随填充率减小而提高。
关键词:椭圆型混合器;二元颗粒;活动层;径向混合
文章编号:1004-0609(2017)-04-0825-08 中图分类号:TF414.2 文献标志码:A
颗粒作为物质存在的普遍形态,是工业生产中非常重要的物料,在药品制备、建材加工、金属冶炼等行业中被广泛应用[1-3],混合器又是工业生产中最常见的设备[4-5],利用混合器对颗粒物料进行干燥、混合等工艺处理也是很多工业中的重要操作单元。因此,研究颗粒物料在混合器内的运动特性和混合规律,对工业生产具有重要的理论指导意义和工程应用价值。
早期,一些学者对圆型混合器内颗粒的径向混合做了大量研究[6-8],其中,赵永志等[9]通过离散单元法模拟了二元颗粒在滚筒内的流动过程,分析了转速、填充率等操作参数对滚筒内二元颗粒分层现象的影响,发现在低转速下,大、小颗粒形成波浪形界面的花瓣模式,高转速下,大颗粒在外,小颗粒在内,形成圆形界面的月亮模式。耿凡等[10]对球磨机内颗粒的复杂混合运动进行数值模拟,研究了颗粒尺寸、密度和粒度不均等物料自身的物理性质对颗粒运动混合特性的影响。陈辉等[11-12]采用离散单元法对圆型滚筒内二元颗粒的混合分离过程进行了数值模拟,运用渗流和凝聚竞争理论定量分析滚落运动模式下物料的径向分离现象,并得出颗粒混合速度随滚筒转速增加而增大的结论。为深入分析圆型混合器内颗粒的运动混合机理,欧阳洪武等[13]实验研究在低速转鼓内颗粒尺寸和颗粒形状影响颗粒活动层厚度的变化情况,发现活动层厚度与转鼓半径和颗粒直径的比值呈线性关系,且活动层厚度随颗粒剪切率的增大而减小。AMARA等[14]建立新的理论模型,讨论了颗粒的活动层厚度在不同填充率、不同转速和不同颗粒尺寸下的变化规律。
研究表明,影响混合器内颗粒混合程度的因素除颗粒的物理性质、操作参数外,还有混合器的结构形状。近些年,越来越多的研究者在探究颗粒的运动混合时,转向了对混合器结构形状的研究上。JIANG等[15]分别采用中心设置“-”型、“+”型与“*”型挡板的圆型混合器进行二元颗粒的混合实验,结果表明,挡板能够有效增强颗粒之间混合。张立栋等[16]研究了滚筒内壁抄板形式对二元颗粒混合程度的影响,发现滚筒内壁设弯抄板的混合程度优于内壁设直抄板。李少华等[17]和闫明等[18]又都对比分析了圆形、椭圆形和方形内壁回转装置内颗粒的混合过程,结果表明混合器形状差异对二元颗粒的混合稳定性有很大影响。GUI等[19]模拟颗粒在波纹形内壁回转装置内的混合过程,发现低转速下,颗粒在回转装置内发生周期性的振荡运动,这种振荡运动提高了颗粒的混合。
虽然国内外学者从多方面对混合器内颗粒的运动混合规律进行了大量研究,但是针对二元颗粒在椭圆型混合器的研究很少[20],仅仅处于探索中。因此,本文作者采用实验方法将深入研究转速ω、填充率f等因素对椭圆型混合器内二元颗粒径向混合的影响。
1 实验
1.1 实验条件
实验装置如图1所示,由6个主要部件组成,其中,调速仪控制混合器的旋转速度,图像采集装置进行在线连续采样[21-22],捕捉、记录混合器内颗粒的整个运动过程,并传输和保存于计算机中。选取的实验混合器是3个不同尺寸的椭圆型混合器和1个圆型混合器,3个椭圆型混合器的长、短轴尺寸比分别为100:80(即离心率e=0.6)、100:85(e=0.527)和100:90 (e=0.436),圆型混合器直径为100 mm(e=0),4个混合器的内部厚度均为12 mm,混合器材料为中碳钢,其硬度约为HRC55,封盖材料是透明玻璃。实验物料采用直径1 mm和3 mm的轴承钢GCr15钢球颗粒,硬度为HRC62~66,密度为7850 kg/m3,钢球与钢球、钢球与混合器内壁的摩擦因数均为0.15。
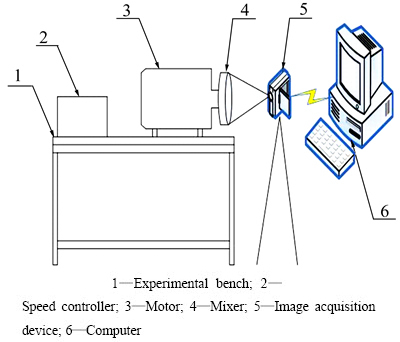
图1 实验装置
Fig. 1 Experimental device
开始转动前,椭圆型混合器处于其长轴垂直于水平方向的位置,两种不同粒径颗粒按体积比1:1向混合器内填充,且1 mm颗粒在下部,3 mm颗粒在上部,如图2所示。实验工况中的转速ω分别为3、9和15 r/min,填充率f分别是1/6、1/3、1/2,所有工况下的颗粒运动均为滚落运动模式。

图2 混合器转动前颗粒初始状态
Fig. 2 Initial state of particles before mixer rotating
1.2 图像处理
通过MATLAB软件对拍摄的实验视频进行一系列图像处理[23]:等时间间隔截图、图片分割、样本图片中大小颗粒筛分、提取样本图片中大小颗粒数量,最后将得到的每个样本中大小颗粒数量用于计算混合指数。
2 混合评价方法
国内外有多种关于颗粒混合程度的评价方法,比较常用且可定量分析的有:变异系数法、接触数、混合熵和Lacey混合指数。其中,变异系数法受网格划分取样的局部影响较大,更适合对混合器内轴向混合程度的评价;接触数对颗粒的接触数量统计要求很高,处理实验中的颗粒混合很难实现,主要应用于数值模拟;混合熵的评价精度与网格的划分尺寸有密切关系,有时不能正确区分混合差异较大的两个样本;Lacey混合指数虽然在不同的网格划分取样下也会有很大差异,但是李少华等[24]通过研究不同取样方式对Lacey混合指数的影响,得出最佳的取样尺寸,即略大于颗粒最佳混合时的横向尺寸,而且Lacey混合指数适合对实验中的径向颗粒混合进行处理分析。因此,本文作者采用Lacey混合指数作为混合器内颗粒混合质量的评价方法。
Lacey混合指数计算式:
 (1)
(1)
式中: 为两种颗粒完全分离时的混合方差;S2为实际的混合方差;
为两种颗粒完全分离时的混合方差;S2为实际的混合方差; 为完全随机混合时的混合方差。
为完全随机混合时的混合方差。
由式(1)可得,Lacey混合指数M的变化范围为[0,1],M值越大,表示颗粒的混合越均匀;当M=1时,颗粒混合达到理想的完全混合状态。
3 结果与分析
3.1 混合器内颗粒混合过程与机理分析
图3所示为ω=3 r/min、f=1/3时4个混合器内二元颗粒运动过程的Lacey混合指数变化情况。由于椭圆型混合器相对圆型混合器的几何特殊性,以转动圈数C替代时间为自变量,混合器每转过1/4圈截取一张图片,进行处理并计算Lacey混合指数。
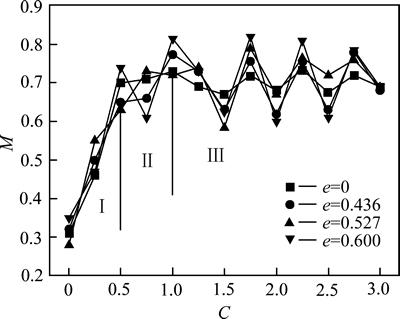
图3 ω=3 r/min、f=1/3时不同混合器中Lacey混合指数曲线示意图
Fig. 3 Schematic diagram of mixing index Lacey for different mixers at ω=3 r/min and f=1/3
颗粒在混合器中的运动是混合与偏析共存的过程,而颗粒的混合又包括对流、剪切和扩散3种机制。在混合器内,颗粒混合并不是某种机制单一发挥作用,而是对流、剪切和扩散三者共同作用的结果,但是在混合过程的不同阶段,3种机制各自对颗粒混合效果的影响程度却不同。
从图3可以看出,4个混合器所对应的混合曲线变化趋势基本一致,Lacey指数随转动圈数增加先急剧增大,然后增速变缓,最后趋于平缓。由此得出,颗粒的混合过程一般可分为3个阶段:
1) 快速混合阶段,此阶段的混合主要是对流机制起作用。在最初填充颗粒时,二元颗粒几乎处于分离状态,混合指数很低,伴随混合器转动,颗粒在内壁提升力作用下开始运动,颗粒体系转动到动态休止角度时,自由表面的颗粒受重力驱动快速滑落,此时,二元颗粒之间整体产生较大相对滑移量,宏观运动是影响混合效果的主要原因,因此,混合速度非常快,Lacey指数急剧上升。
2) 缓慢混合阶段,此阶段的混合主要是对流和剪切机制的共同作用。伴随混合器内颗粒的随机运动,二元颗粒之间的接触量越来越多,相反,它们的整体相对滑移量却逐渐变小,对流作用相应减弱。同时,自由表面中二元颗粒在重力作用下处于惯性流流态[25],颗粒之间发生频繁的碰撞,相互传递动量,从而产成速度差异,导致颗粒间局部的相互滑移,剪切混合开始凸出。此阶段的混合程度依然逐渐增加,但是颗粒之间的偏析作用开始加强,致使混合速度变慢,Lacey指数的增长也逐渐变缓。
3) 波动混合阶段,此阶段的混合主要是扩散机制起作用。二元颗粒在混合器内形成相对稳定的周期流动,对流与剪切机制对颗粒的混合仍然发挥重要作用,但是它们不再是进一步影响混合效果的主要原因。稳定流动状态中,出现大颗粒在外围,小颗粒在内部的分层现象,混合均匀度的提高是通过分界面两侧内的二元颗粒相互渗透,作微小的随机移动,形成局部扩散来完成,扩散最终决定了二元颗粒混合的均匀度。在稳定流动阶段,颗粒的偏析作用依然不断增强,并开始出现偏析强于混合的现象(如图3中1~1.5圈之间Lacey指数减小),但是混合作用一直存在,两者共存并相互制约,最终,混合与偏析达到动态平衡,Lacey混合指数趋于平缓,在某一值上下波动。
在波动混合阶段,整体来看,二元颗粒在椭圆型混合器内混合指数的波动幅度明显大于在圆型混合器内,且混合器的离心率越大,二元颗粒的混合指数波动幅度越大,如图4所示,这说明,在相同操作条件下,二元颗粒在椭圆型混合器内的混合稳定性较圆型混合器内差,而且,混合稳定性随混合器离心率的增大变的更差。这是因为,椭圆型混合器受自身特殊形状的影响,运动到不同位置时,颗粒体系所获得的重力势能不同,当由竖直位置转动到水平位置时,颗粒体系的整体重力势能增加[17],椭圆型混合器的离心率越大,颗粒体系在这两种位置交替时的重力势能变化越大,相应地,自由表面中流动颗粒的速度波动越大,颗粒的随机无序运动变化越显著,因此,混合的稳定性越差。

图4 不同混合器内颗粒在波动混合阶段混合指数波动幅度变化示意图
Fig. 4 Schematic diagram of fluctuation range of particle mixing index in different mixers in period of wave mixing
3.2 椭圆型混合器内滚落运动模式理论模型
颗粒在回转装置内的运动主要有6种模式[26]:滑移、阶梯、滚落、泄落、抛落和离心。实际工程应用中,滚落是最常见的运动模式,也被认为具有最高的混合效率,国内外研究者对圆型回转装置内颗粒处于滚落模式的研究做了大量工作并得出结论:处于滚落模式的颗粒体系分为活动层和平流层两个区域[27],如图5(a)所示,活动层的颗粒向下快速运动并形成稳定的自由下滑面2L和动态休止角θ,平流层的颗粒随回转装置以相同转速运动,颗粒之间相对静止。
活动层内,颗粒速度矢量混乱无序,是颗粒混合的重要区域,活动层的颗粒状态及区域范围的变化都对混合有很大影响,因此,为深入分析颗粒在椭圆型混合器内的运动混合过程,有必要对椭圆型混合器内颗粒的活动层进行研究。
圆型回转装置内的活动层,有稳定的自由下滑面2L和动态休止角θ,而对于椭圆型混合器,通过实验观察,由于长短轴的不对称性,活动层的自由下滑面伴随混合器转动会发生明显的周期性变化,但动态休止角是否发生变化,肉眼并不能直接观察出来,因此,为定量的体现自由下滑面的长度变化和确定动态休止角是否发生变化,需要对视频的截图进行测量计算。
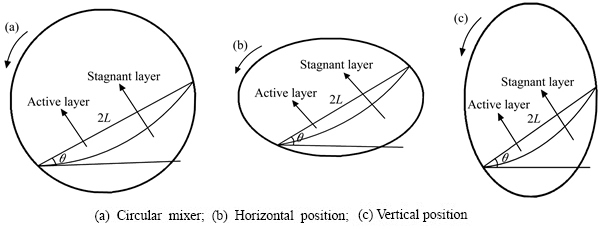
图5 滚落模式中活动层和平流层示意图
Fig. 5 Schematic diagram of active layer and stagnant layer in rolling regime
椭圆型混合器在转动过程中,有两个特征显著的位置:水平位置(长轴平行于水平方向)和竖直位置(长轴垂直于水平方向),如图5(b)和(c)所示,因此,本文作者主要对这两个位置的活动层变化进行讨论分析。以离心率e=0.6的椭圆型混合器为研究对象,分别对不同转速、不同填充率下的混合器达到混合稳定状态时,在水平位置和竖直位置的图片各取10张,测量每张图片中活动层的自由下滑面长度和动态休止角,然后,对自由下滑面长度的所有测量值取平均值,对动态休止角的所有测量值取其中最大值,结果显示:1) 同一工况下,两种位置的动态休止角几乎相等;填充率一定时,动态休止角随转速的增大而增大,见表1;2) 同一工况下,椭圆型混合器在水平位置时的自由下滑面长度大于在竖直位置时的长度;填充率f不大于1/2时、转速一定,相同位置的自由下滑面长度随填充率的增大而增大(见表2)。
AMARA等[14]研究圆型回转装置内活动层的厚度变化,本文作者在他的研究基础之上,将对二元颗粒在椭圆型混合器横截面上的运动形态进行几何分析,计算得到椭圆型混合器内活动层面积(见图6)。如图6所示,活动层与平流层的分界线是以A(0,0)、B(xb,yb)为端点的一段圆弧,这段圆弧与自由下滑面长度所围成的几何面积S就是活动层的区域范围。
表1 1/3填充率、不同转速时两种位置的动态休止角θ
Table 1 Variation of dynamic angle of repose θ with rotational speed at f=1/3 in two kinds of position
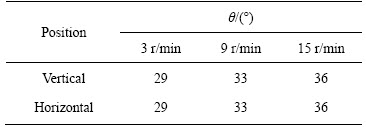
表2 9 r/min转速、不同填充率时两种位置的自由下滑面长度2L
Table 2 Variation of with length 2L of free surface with filling ratio at ω=9 r/min in two kinds of position


图6 椭圆型混合器径向截面几何分析
Fig. 6 Geometric analysis of transverse section for elliptical mixer
根据几何知识,可得
 (2)
(2)
其中,线段D的长度:
 (3)
(3)
1/2自由下滑面长度L:
 (4)
(4)
活动层厚度E:
 (5)
(5)
动态休止角θ值:
 (6)
(6)
以曲线AB为圆弧的圆,圆心O(xO,yO)半径R:
 (7)
(7)
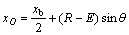 (8)
(8)
 (9)
(9)
又:
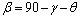 (10)
(10)
 (11)
(11)
在式(2)~(11)中,其中,1/2自由下滑面长度L、动态休止角θ和B(xb, yb)可从图片测量中获得,最后,用O(xO, yO)、A(0, 0)、B(xb, yb) 3点组成的扇形面积减去3点组成的三角形面积,即得到活动层面积S:
 (12)
(12)
椭圆型混合器内活动层面积的计算结果如图7所示,其中,图7(a)为混合器在ω=9 r/min、分别处于竖直位置和水平位置时,活动层面积随填充率变化的对比图;图7(b)为混合器在f=1/3、分别处于竖直位置和水平位置时,活动层面积随转速变化的对比图。结果表明:同一工况下,椭圆型混合器处于竖直位置时,颗粒的活动层面积大于水平位置时;同在水平或垂直位置时,颗粒的活动层面积随填充率的增大而减小,随转速的增大而增大。
3.3 转速和填充率对椭圆型混合器内颗粒混合的影响
以离心率e=0.6的椭圆型混合器为研究对象,分析转速和填充率对颗粒混合的影响。图8所示为不同工况下椭圆型混合器内Lacey混合指数的对比。由图8可以看出,在相同转速下,填充率越小,椭圆型混合器内颗粒的混合程度越高,由于填充率减小,颗粒数量减少,大、小颗粒之间的运动接触越容易,并且,活动层面积随填充率的减小而增大,活动层内的颗粒比例上升,参与混合运动的颗粒增多。从图8中还可看出,部分工况下,颗粒的缓慢混合阶段并不明显,或者会消失,由快速混合阶段直接进入波动混合阶段,且转速越大,颗粒达到波动混合阶段所需的圈数越多,即在以圈数为自变量的情况下,颗粒的混合速度随转速增大而降低,这与陈辉等[12]的研究结果一致。高转速下,填充率较低时,颗粒的混合稳定性会变差,这是由于,混合器内活动层的面积随转速的提高而增大,因此,伴随椭圆型混合器长短轴的交替变化,活动层内速度波动较大的颗粒数量增多。而对于填充率较高的混合器,活动层的区域范围占总颗粒区域范围的比例很小,由于转速提高而增加的活动层面积占总颗粒区域面积的比例更是微小,不足以影响颗粒的稳定性发生显著性变化。

图7 不同工况下的椭圆型混合器在两种位置处活动层的面积
Fig. 7 Active layer area of elliptical mixer in two different locations under different operating conditions
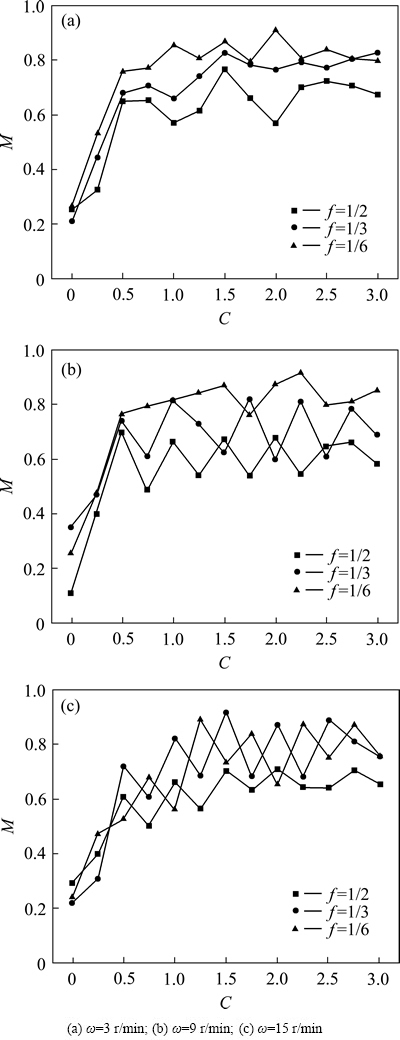
图8 不同工况下椭圆型混合器内Lacey混合指数的对比
Fig. 8 Comparison of mixing index Lacey in elliptical mixer at different operating conditions
4 结论
1) 在波动混合阶段,椭圆型混合器的离心率越大,二元颗粒的混合稳定性越差。
2) 同一工况下,椭圆型混合器在竖直位置和水平位置的颗粒动态休止角相等,自由下滑面长度不相等;填充率一定时,动态休止角随转速的增大而增大;填充率不大于1/2时、转速一定,相同位置的自由下滑面长度随填充率的增大而增大。
3) 同一工况下,椭圆型混合器处于竖直位置的活动层面积大于水平位置的活动层面积;在同一位置,颗粒的活动层面积随填充率的增大而减小,随转速的增大而增大。
4) 转速一定时,填充率越小,椭圆型混合器内颗粒的混合程度越高;低填充率下,转速较高时,椭圆型混合器内颗粒的混合稳定性较差。
REFERENCES
[1] LI S Q, CHI Y, LI R D, YAN J H, CEN K F. Axial transport and residence time of MSW in rotary kilns: Part II. Theoretical and optimal analyses[J]. Powder Technology, 2002, 126(3): 228-240.
[2] LI R, LI Y C, HOU M Y. Phase separation in a three dimensional granular gas system[J]. Acta Physica Sinica, 2008, 57(8): 4660-4666.
[3] 欧阳鸿武, 何世文, 廖奇音, 韦 嘉. 3种二组元粉体的混合特征[J]. 中国有色金属学报, 2004, 14(5): 746-751.
OUYANG Hong-wu, HE Shi-wen, LIAO Qi-yin, WEI Jia. Mixing characteristics of three kinds of two-component powders in rotating drum blender[J]. The Chinese Journal of Nonferrous Metals, 2004, 14(5): 746-751.
[4] 贺实月, 李会泉, 李少鹏, 李勇辉, 解 强. 煤粉炉高铝粉煤灰碱溶脱硅反应动力学[J]. 中国有色金属学报, 2014, 24(7): 1888-1894.
HE Shi-yue, LI Hui-quan, LI Shao-peng, LI Yong-hui, XIE Qiang. Kinetics of desilication process of fly ash with high aluminum from pulverized coal fired boiler in alkali solution[J]. The Chinese Journal of Nonferrous Metals, 2014, 24(7): 1888-1894.
[5] 马德刚, 陈伟庆, 车晓梅. 炼镍转炉溅渣护炉的水模试验[J]. 中国有色金属学报, 2012, 12(1): 287-295.
MA De-gang, CHEN Wei-qing, CHE Xiao-mei. Hydraulic simulation of slag splashing in nickel converter[J]. The Chinese Journal of Nonferrous Metals, 2012, 12(1): 287-295.
[6] HILL K M, KHAKHAR D V, GILCHRIST J F, McCarthy J J, Ottino J M. Segregation-driven organization in chaotic granular flows[J]. Proc Natl Acad Sci, 1999, 96(21): 11701-11706.
[7] JAIN N, OTTINO J M, LUEPTOW R M. Combined size and density segregation and mixing in noncircular tumblers[J]. Phys, 2005, 71(5): 1-10.
[8] CISA S E, UMBANHOWAR P B, OTTINO J M. Radial granular segregation under chaotic flow in two-dimensional tumblers[J]. Phys, 2006, 74(5): 1-12.
[9] 赵永志, 程 易. 水平滚筒内二元颗粒体系径向分离模式的数值模拟研究[J]. 物理学报, 2008, 57(1): 322-328.
ZHAO Yong-zhi, CHENG Yi. Numerical simulation of radial segregation patterns of binary granular systems in a rotating horizontal drum[J]. Acta Physica Sinica, 2008, 57(1): 322-328.
[10] 耿 凡, 袁竹林, 孟德才, 李善莲. 球磨机中颗粒混合运动的数值模拟[J]. 热能动力工程, 2009, 24(5): 623-629.
GENG Fan, YUAN Zhu-lin, MENG De-cai, LI Shan-lian. Numerical simulation of particle mixing in ball mill[J]. Journal of Engineering for Thermal Energy and Power, 2009, 24(5): 623-629.
[11] 陈 辉, 赵先琼, 刘义伦, 肖友刚, 刘 颖. 转筒内D型二元颗粒物料滚落模式的径向分离[J]. 农业机械学报, 2015, 46(6): 334-340.
CHEN Hui, ZHAO Xian-qiong, LIU Yi-lun, XIAO You-gang, LIU Ying. Transverse separation of D-type binary dispersed granular materials with rolling regime in cylinder drum[J]. Transactions of the Chinese Society for Agricultural Machinery, 2015, 46(6): 334-340.
[12] 陈 辉, 刘义伦, 赵先琼, 肖友刚, 刘 颖. 一元散体颗粒物料在回转窑界面上的运动与混合[J]. 中国有色金属学报, 2015, 25(5): 2575-2581.
CHEN Hui, LIU Yi-lun, ZHAO Xian-qiong, XIAO You-gang, LIU Ying. Motion and mixing of mono-disperse granular material in cross section of rotary kiln[J]. The Chinese Journal of Nonferrous Metals, 2015, 25(5): 2575-2581.
[13] 欧阳鸿武, 张 新, 黄誓成, 王 琼, 刘卓明. 转鼓中颗粒流动层厚度及其影响因素[J]. 粉末冶金材料科学与工程, 2008, 13(2): 84-90.
OUYANG Hong-wu, ZHANG Xin, HUANG Shi-cheng, WANG Qiong, LIU Zhuo-ming. Thickness of granular flowing layer and its influencing factors in rotating drum[J]. Materials Science and Engineering of Powder Metallurgy, 2008, 13(2): 84-90.
[14] AMARA A A, CARL D, DENIS R. Transverse mixing of polymer powders in a rotary cylinder part I: Active layer characterization[J]. Powder Technology, 2012, 219(3): 99-106.
[15] JIANG M Q, ZHAO Y Z, LIU G S, ZHENG J Y. Enhancing mixing of particles by baffles in a rotating drum mixer[J]. Particuology, 2011, 9(3): 270-278.
[16] 张立栋, 李少华, 朱明亮, 张 轩, 余侃胜, 王 擎, 郝万军. 回转干馏炉内抄板形式与双组元颗粒混合过程冷模数值研究[J]. 中国电机工程学报, 2012, 32(11): 72-78.
ZHANG Li-dong, LI Shao-hua, ZHU Ming-liang, ZHANG Xuan, YU Kan-sheng, WANG Qing, HAO Wan-jun. Cold mode numerical analysis of flights forms and two component particles mixing in rotary retorting[J]. Proceedings of the CSEE, 2012, 32(11): 72-78.
[17] 李少华, 王丽伟. 回转炉内壁炉型结构对颗粒混合效果的影响[J]. 煤炭学报, 2013, 38(10): 1878-1881.
LI Shao-hua, WANG Li-wei. Effects of the particle mixed on furnace inner structure of rotary kiln[J]. Journal of China Coal Society, 2013, 38(10): 1878-1881.
[18] 闫 明, 段文山, 陈 琼, 周志刚, 张 昱, 赵 闯, 厚美瑛. 不同形状混合器中二元颗粒的分聚与混合研究[J]. 力学学报, 2016, 48(1): 64-75.
YAN Ming, DUAN Wen-shan, CHEN Qiong, ZHOU Zhi-gang, ZHANG Yu, ZHAO Chuang, HOU Mei-ying. The segregation and mixing of binary granular systems in rotating mixer with different cross-sections[J]. Chinese Journal of Theoretical and Applied Mechanics, 2016, 48(1): 64-75.
[19] GUI N, FAN J. Numerical study of heat conduction of granular particles in rotating wavy drums[J]. International Journal of Heat and Mass Transfer, 2015, 84: 740-751.
[20] LI D, LIU G D, LU H L, ZHANG Q H, WANG Q, YU H B. Numerical simulation of different flow regimes in a horizontal rotating ellipsoidal drum[J]. Powder Technology, 2015, 291(6): 86-96.
[21] SUDA O S, COFFIN B D, MUZZIO F J. Quantitative characterization of mixing of free-flowing granular material in tote(bin)-blenders[J]. Powder Technology, 2002, 226(2): 191-200.
[22] BROADBEN C J, BRIDGWATER J, PARKER D J, KENINGLEY S T, KNIGHT P. A phenomenological study of a batch mixer using a position camera[J]. Powder Technology, 1993, 76(3): 317-329.
[23] 张立栋, 刘朝青, 朱明亮, 于丁一, 李少华, 王 擎. 基于图像处理的回转滚筒内颗粒群提取方法[J]. 中国粉体技术, 2013, 19(4): 42-45.
ZHANG Li-dong, LIU Chao-qing, ZHU Ming-liang, YU Ding-yi, LI Shao-hua, WANG Qing. Extraction method of particle groups based on image processing in rotary drum[J]. China Powder Science and Technology, 2013, 19(4): 42-45.
[24] 李少华, 朱明亮, 张立栋, 王 擎, 刘朝青, 于丁一. 回转装置内三组元颗粒径向混合评价方法分析[J]. 化工进展, 2013, 32(6): 1224-1229.
LI Shao-hua, ZHU Ming-liang, ZHANG Li-dong, WANG Qing, LIU Chao-qing, YU Ding-yi. Analysis of three-component radial mixing evaluation methods in rotary retorting[J]. Chemical Industry and Engineering Progress, 2013, 32(6): 1224-1229.
[25] 孙其诚, 王光谦. 颗粒物质力学导论[M]. 北京: 科学出版社, 2009: 103-107.
SUN Qi-cheng, WANG Guang-qian. An introduction to the mechanics of granular materials[M]. Beijing: Science Publishing company, 2009: 103-107.
[26] MELLMANN J. The transverse motion of solids in rotating cylinders-forms of motion and transition behavior[J]. Powder Technology, 2001, 118(3): 251-270.
[27] LEHMBERG J, HEHL M, SCHUGERL K. Transverse mixing and heat transfer in horizontal rotary drum reactors[J]. Powder Technology, 1977, 18(2): 149-163.
Transverse mixing of binary granular in elliptical mixer
ZHANG Li-dong1, LI Lian-hao1, WANG Qing1, QIN Hong1, LI Shao-hua2
(1. School of Energy Resource and Power Engineering, Northeast Dianli University, Jilin 132012, China;
2. Science and Technology Research Institute Co., Ltd., China Datang Corporation, Beijing 102206, China)
Abstract: In order to evaluate the quality of mixing, the effects of filling ratio and rotational speed on transverse mixing of binary granular in an elliptical mixer operated in the rolling regime were studied adopting experimental and theoretical approaches based on mixing index Lacey. The results indicate that the centrifugal rate of the elliptical mixer affects the mixing stability of binary granular in the wave mixing stage. For the same operating condition, the dynamic angle of repose in horizontal position and vertical position of the elliptical mixer are equal. When the filling ratio is constant, the dynamic angle of repose increases with the increase of rotational speed, however, the filling ratio is not larger than 1/2, the length of active layer with free surface increases with the increase of the filling ratio at the same rotational speed increasing. For the same operating condition, the area of the active layer in the vertical position is bigger than that in the horizontal position. The area of the active layer decreases with the filling ratio increasing, and increases with the rotational speed increasing in the same elliptical cylinder position. The mixing degree of granular increases with the decrease of filling ratio at a fixed rotational speed.
Key words: elliptical mixer; binary granular; active layer; transverse mixing
Foundation item: Project(IRT13052) supported by Program of Changjiang Scholars and Innovative Research Team in University, China; Project(20150101033JC) supported by the Natural Science Foundation of Jilin Province, China; Project(201464044) supported by the Science and Technology Development Projects of Jilin City, China; Project(2015-237) supported by the Development of Education of Jilin Province, China
Received date: 2016-03-11; Accepted date: 2016-07-07
Corresponding author: ZHANG Li-dong; Tel: +86-13843225181; E-mail: nedu1015@aliyun.com
(编辑 李艳红)
基金项目:教育部长江学者和创新团队发展计划(IRT13052);吉林省自然科学基金资助项目(20150101033JC);吉林市科技计划项目(201464044);吉教科合字资助的课题(2015-237)
收稿日期:2016-03-11;修订日期:2016-07-07
通信作者:张立栋,副教授,博士;电话:13843225181;E-mail: nedu1015@aliyun.com